本时间序列分析第四章小结
- 格式:ppt
- 大小:570.50 KB
- 文档页数:2
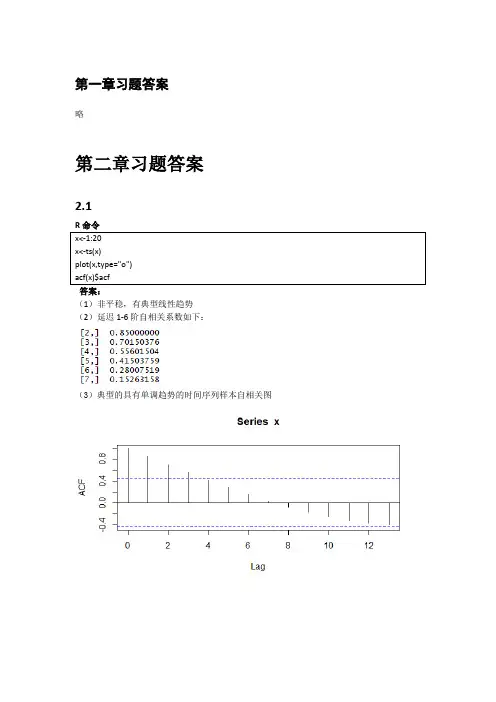
第一章习题答案略第二章习题答案2.1答案:(1)非平稳,有典型线性趋势(2)延迟1-6阶自相关系数如下:(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)1-24阶自相关系数如下(3)自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案:我们自定义函数,计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11(2)差分序列平稳,非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。

第四章:非平稳序列的确定性分析题目一:()()()()()()()12312123121231ˆ14111ˆˆ2144451.1616T T T T T T T T T T T T T T T T T T T T T xx x x x xx x x x x x x x x x x x x x x -------------=+++⎡⎤=+++=++++++⎢⎥⎣⎦=+++ 题目二:因为采用指数平滑法,所以1,t t x x +满足式子()11t t t x x x αα-=+-,下面式子()()11111t t t t t tx x x x x x αααα-++=+-⎧⎪⎨=+-⎪⎩ 成立,由上式可以推导出()()11111t t t t x x x x αααα++-=+-+-⎡⎤⎣⎦,代入数据得:2=5α. 题目三:()()()21221922212020192001ˆ1210101113=11.251ˆ 1010111311.2=11.04.5ˆˆˆ10.40.6.i i i xxxx x x x x αα-==++++=++++===+-=⋅∑(1)(2)根据程序计算可得:22ˆ11.79277.x= ()222019181716161ˆ2525xx x x x x =++++(3)可以推导出16,0.425a b ==,则425b a -=-. 题目四:因为,1,2,3,t x t t ==,根据指数平滑的关系式,我们可以得到以下公式:()()()()()()()()()()()()()()()221221 11121111 1111311. 2t t t t t tt x t t t x t t αααααααααααααααααααα----=+-------=-+---+--+++2+, ++2+用(1)式减去(2)式得:()()()()()221=11111.t t tt x t αααααααααααα-------------所以我们可以得到下面的等式:()()()()()()122111=11111=.t t t tt x t t αααααααα+-----------------()111lim lim 1.ttt ttxt tααα+→∞→∞----==题目五:1. 运行程序:最下方。



第四章时间序列分析每一个时间序列都是事物变化过程中的一个样本,通过对样本的研究、分析,找出过程的特性、最佳的数学模型、估计模型中的参数,检验利用数学模型进行统计预测的精度。
如同描述随机变量一样,利用随机过程的一些数字特征来描述随机时间序列的基本统计特性。
地理要素的空间分布规律是地理系统研究的中心内容。
但是空间与时间是客观事物存在的形式,两者之间是互相联系而不能分割的。
因此,我们常常要分析要素在时间上的变化,在地理系统研究中,就称为地理过程。
据此来阐明地理现象发展的过程和规律。
1.通过对时间序列的研究,阐明对象发展的过程和规律。
现在的现象,往往必须从历史发展中寻找原因和依据。
这和其它学科是共同的。
2.时间上的变化是地理系统的本质特征。
很难找到在时间上不发生变化的地理系统,不同地区的不同变化速率,构成空间变化的主要特征。
3.空间差异有时还可以理解为特定区域地理系统或其要素的时间上变化在区域上的“投影”。
对同一种要素在一定时期的连续观察就确定出现象的时间序列。
许多时间序列的分析都是利用图解法来解决的。
在这种图象中,横轴是时间测度,纵轴是所研究的要素的数值。
第一节时间序列分析基本方法时间序列分析是地理预测的过程,主要研究地理要素及地理活动的时间变化趋势、季节变化、周期变化和不规则变化等规律。
一、图象法时间序列图象有两种表示方法:严格地说,线状图只能用于图象上与变量数值有关的每一点都与时间相对应的情况,例如逐日平均气温图象、人口增长图象等等。
如果变量数值是与各个时段有关,例如:月雨量、年出生率、24小时客流量,这种情况则用柱状图象表示更为合适。
但是,线状图也常用于表示与时段有关的变量。
这是因为线状图容易画、省时间,并且几条线可以叠加在一起,易于比较其趋势。
不过应该注意,不能用与时段有关的线状图进行内插求值。
这是因为一个时段内的每一点,并没有相对应的值。
比如,从年出生率线状图中,不能求出瞬时的或日、月的出生率。



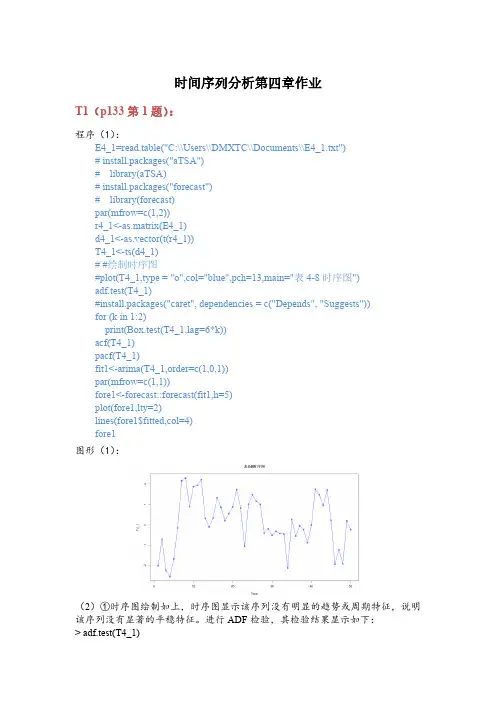
时间序列分析第四章作业T1(p133第1题):程序(1):E4_1=read.table("C:\\Users\\DMXTC\\Documents\\E4_1.txt")# install.packages("aTSA")# library(aTSA)# install.packages("forecast")# library(forecast)par(mfrow=c(1,2))r4_1<-as.matrix(E4_1)d4_1<-as.vector(t(r4_1))T4_1<-ts(d4_1)# #绘制时序图#plot(T4_1,type = "o",col="blue",pch=13,main="表4-8时序图")adf.test(T4_1)#install.packages("caret", dependencies = c("Depends", "Suggests"))for (k in 1:2)print(Box.test(T4_1,lag=6*k))acf(T4_1)pacf(T4_1)fit1<-arima(T4_1,order=c(1,0,1))par(mfrow=c(1,1))fore1<-forecast::forecast(fit1,h=5)plot(fore1,lty=2)lines(fore1$fitted,col=4)fore1图形(1):(2)①时序图绘制如上,时序图显示该序列没有明显的趋势或周期特征,说明该序列没有显著的平稳特征。
进行ADF检验,其检验结果显示如下:> adf.test(T4_1)Augmented Dickey-Fuller Testalternative: stationaryType 1: no drift no trendlag ADF p.value[1,] 0 -3.60 0.01[2,] 1 -3.19 0.01[3,] 2 -3.30 0.01[4,] 3 -3.20 0.01Type 2: with drift no trendlag ADF p.value[1,] 0 -3.65 0.0100[2,] 1 -3.23 0.0256[3,] 2 -3.44 0.0165[4,] 3 -3.48 0.0148Type 3: with drift and trendlag ADF p.value[1,] 0 -3.70 0.0340[2,] 1 -3.29 0.0833[3,] 2 -3.64 0.0388[4,] 3 -3.94 0.0193----Note: in fact, p.value = 0.01 means p.value <= 0.01检验结果显示,该序列所有ADF检验统计量的P值均小于显著性水平(α=0.05),所以可以确定该系列为平稳序列;②对平稳序列进行纯随机性检验,其检验结果如下:Box-Pierce testdata: T4_1X-squared = 25.386, df = 6, p-value = 0.0002896Box-Pierce testdata: T4_1X-squared = 31.153, df = 12, p-value = 0.001867结果显示6阶和12阶延迟的LB统计量的P值都小于显著性水平(α=0.05),所以可以判断该系列为平稳非白噪声序列。

时间序列分析报告心得一、引言时间序列分析是一门研究按一定时间顺序排列的数据并通过统计方法对其进行建模、预测和分析的方法。
在时间序列分析的过程中,我们运用了各种统计技术,比如平均数、标准差等,通过对历史数据的分析,我们可以预测未来一段时间内的数据变化趋势和规律。
本篇报告主要总结了我对时间序列分析的学习和实践的心得体会。
二、学习过程在学习时间序列分析的过程中,我首先了解了时间序列分析的基本概念和常用的方法。
我了解到,时间序列分析的目标是通过分析时间序列的内在规律,对未来的发展趋势进行预测。
同时,时间序列分析也可以揭示时间序列中的周期性变化、趋势性变化和季节性变化。
我学习了一些时间序列分析的基本概念,比如平稳性、自相关函数、移动平均、自回归等。
在学习过程中,我尝试了不同的学习方法。
首先,我阅读了一些经典的时间序列分析教材和文献,掌握了基本的理论知识。
其次,我通过在线课程和视频教程学习了时间序列分析的实践技巧。
最后,我参与了一些实际项目,应用时间序列分析模型对数据进行预测和分析。
三、实践应用在时间序列分析的实践应用中,我主要应用了Python编程语言和一些常用的时间序列分析工具包,比如pandas和statsmodels。
通过这些工具,我可以对时间序列数据进行读取、处理、分析和可视化。
我首先通过pandas库读取了时间序列数据,并进行了数据的预处理工作。
预处理包括填充缺失值、平滑数据、去除异常点等步骤,这可以使得模型更准确地反映数据的真实情况。
然后,我使用了statsmodels库来构建时间序列分析模型。
statsmodels库提供了丰富的时间序列模型类和函数,比如ARIMA模型、SARIMA模型等。
通过这些模型,我可以对时间序列数据进行建模和预测。
最后,我使用了matplotlib库对分析结果进行可视化。
可视化可以帮助我们更直观地理解数据的规律和趋势,以及模型的预测效果。
四、心得体会通过学习和实践时间序列分析,我深刻体会到了时间序列分析在实际应用中的重要性和价值。

概率与数理统计第4章时间序列分析第4章时间序列分析[引例]某酿酒公司⽣产⼀种红葡萄酒,这种红葡萄酒颇受市场欢迎,其销售量稳步上升(表4-1),对公司盈利起到重要作⽤。
表4-1 某酿酒公司红葡萄酒销售量单位:件——资料来源:国际通⽤MBA教材配套案例《管理统计案例》机械⼯业出版社1999.3 本章⼩结1.时间序列是把同⼀现象在不同时间上的观察数据按时间先后顺序排列起来所形成的数列,它是动态分析的基础。
时间序列的分析有指标分析和构成因素分析两类。
时间序列的影响因素可归结为长期趋势、季节变动、循环变动和不规则变动等四种,常以乘法模型为基础来进⾏时间序列的分解和组合。
2.⽔平分析指标主要有平均发展⽔平、增减量(逐期、累计)和平均增减量。
不同类型的时间序列计算平均发展⽔平的⽅法有所不同。
累计增减量等于相应逐期增减量之和。
平均增减量是观察期内各个逐期增减量的平均数。
速度分析指标有发展速度、增减速度、平均发展速度和平均增减速度。
定基发展速度也即发展总速度,它等于相应时期内各环⽐发展速度的连乘积。
增减速度等于发展速度减1。
平均发展速度是环⽐发展速度的平均数,其计算⽅法通常采⽤⼏何平均法。
平均增减速度等于平均发展速度减1。
3. 长期趋势的分析⽅法主要有平滑法(移动平均、指数平滑法)和⽅程拟合法。
移动平均关键在于选择平均项数;能消除序列中的季节影响(平均项数与季节周期长度必须⼀致)。
指数平滑法是关键在于确定平滑系数。
⽅程拟合法通常采⽤最⼩⼆乘法来估计趋势⽅程中的参数。
4. 季节⽐率的测定⽅法:原资料平均法和趋势剔除法。
原资料平均法适⽤于⽔平趋势的季节序列;趋势剔除法适⽤于有明显上升(或下降)趋势的季节序列。
当没有季节因素影响时,季节⽐率为1或100%。
序列的季节调整即以原始数据除以对应季节的季节⽐率,⽬的是从时间序列中去掉季节影响,便于分析其它成分。
5.利⽤分析⼯具库中的“移动平均”、“指数平滑法”、“回归”或图表中的添加趋势线功能,可以测定时间序列的长期趋势。
第一节模型的识别单变量时间序列的Box-Jenkins 模型识别方法主要是根据样本自相关和偏自相关函数的截尾和拖尾性来判断序列所适合的模型。
平稳序列的自相关函数和偏自相关函数的统计特性对非零均值序列的处理计算样本均值,将每一序列值减去样本均值。
将序列均值作为一未知参数处理。
例如AR 模型例:,Xt 的均值是多少?判定在m步之后截尾的做法是:判定在n步之后截尾的做法是:拖尾:即被负指数控制收敛于零。
若序列自相关函数和偏自相关函数无以上特征,而是出现缓慢衰减或周期性衰减情况,则说明序列不是平稳的。
例:见演示试验。
第二节模型的定阶自相关函数和偏自相关函数定阶法自相关函数和偏自相关函数不但可以用来进行模型的识别,同样也可以用来进行AR 模型和MA 模型的定阶。
该方法对ARMA 模型定阶较为困难,同时,用该方法定的阶数也只能作为初步参考值。
残差方差定阶法残差方差定阶法借用了统计学中多元回归的原理。
假定模型是有限阶的自回归模型,如果选择的阶数小于真正的阶数,则是一种不足拟合,因而剩余平方和必然偏大,残差方差也将偏大;如果选择的阶数大于真正的阶数,则是一种过度拟合,残差方差并不因此而显著减小。
AR 、MA 、ARMA 三种模型的残差方差估计式分别为:F检验定阶法基本过程:对N个独立的观察值,建立回归模型:若舍弃后面S个因子,另建一个回归模型:检验舍弃的回归因子对Y的影响是否显著,等价于检验原假设:最佳准则函数定阶法对于AR 模型,AIC 函数可取:BIC 定阶理论上AIC 准则不能给出模型阶数的相容估计,即当样本趋于无穷大时,由AIC 准则选择的模型阶数不能收敛到其真值(通常比真值高)。
另一个定阶选择是BIC 准则:对于AR 模型:还可以定义其它类型的准则函数,如自回归移动平均模型的参数矩估计:将模型分成两个部分,先对AR 部分应用YULE-WALKER 方程,计算得到剩余序列,对剩余序列应用MA 模型的参数估计方法。
第四章时间序列分析由于反映社会经济现象的大多数数据是按照时间顺序记录的,所以时间序列分析是研究社会经济现象的指标随时间变化的统计规律性的统计方法。
.为了研究事物在不同时间的发展状况,就要分析其随时间的推移的发展趋势,预测事物在未来时间的数量变化。
因此学习时间序列分析方法是非常必要的。
本章主要内容:1. 时间序列的线图,自相关图和偏自关系图;2. SPSS 软件的时间序列的分析方法−季节变动分析。
§4.1 实验准备工作§4.1.1 根据时间数据定义时间序列对于一组示定义时间的时间序列数据,可以通过数据窗口的Date菜单操作,得到相应时间的时间序列。
定义时间序列的具体操作方法是:将数据按时间顺序排列,然后单击Date →Define Dates打开Define Dates对话框,如图4.1所示。
从左框中选择合适的时间表示方法,并且在右边时间框内定义起始点后点击OK,可以在数据库中增加时间数列。
图4.1 产生时间序列对话框§4.1.2 绘制时间序列线图和自相关图一、线图线图用来反映时间序列随时间的推移的变化趋势和变化规律。
下面通过例题说明线图的制作。
例题4.1:表4.1中显示的是某地1979至1982年度的汗衫背心的零售量数据。
试根据这些的数据对汗衫背心零售量进行季节分析。
(参考文献[2])解:根据表4.1的数据,建立数据文件SY-11(零售量),并对数据定义相应的时间值,使数据成为时间序列。
为了分析时间序列,需要先绘制线图直观地反映时间序列的变化趋势和变化规律。
具体操作如下:1. 在数据编辑窗口单击Graphs→Line,打开Line Charts对话框如图4.2.。
从中选择Simple单线图,从Date in Chart Are 栏中选择Values of individual cases,即输出的线图中横坐标显示变量中按照时间顺序排列的个体序列号,纵坐标显示时间序列的变量数据。