波利亚的解题理论
- 格式:pptx
- 大小:1.48 MB
- 文档页数:20




波利亚解题理论在高三圆锥曲线复习课中的教学案例研究《波利亚解题理论在高三圆锥曲线复习课中的教学案例研究》是本次研究的主题,波利亚解题理论是由意大利数学家阿隆索波利亚所提出的一种解决复杂数学问题的方法,他首先使用此理论解决三角函数问题,本次研究主要是研究该理论在高三圆锥曲线复习课中的应用。
一、波利亚解题理论的背景阿隆索波利亚(Arono B. Poli)是20世纪意大利数学家,他提出了一套叫做“波利亚解题理论”的数学方法,该方法又被称为“波利亚公式”。
这套理论的核心思想是“把一个复杂的问题分解成几个小问题,并且用具体的步骤来解决”。
这套理论的本质是动态解题法,即从反方向出发,先求解具体步骤,最后归纳出总体解法。
波利亚先生认为,数学学习只有通过实践来实现才能真正理解,而不是去学习繁杂的知识点。
二、波利亚解题理论在高三圆锥曲线复习课中的应用圆锥曲线是数学中一个重要的课题,学习这一类型的曲线,要求学生能够熟练掌握解方程的方法和计算圆锥曲线的坐标位置,但很多学生对此感到无从下手,屡屡重复犯同样的错误。
为此,本课程采用了“波利亚解题理论”的教学方法来解决一些典型的圆锥曲线问题,以帮助学生熟练掌握圆锥曲线的解方程法。
(1)课前准备本次课程内容包括从角度、离心率以及圆锥曲线的解方程等等,可以根据学生的不同学习水平来灵活调整每节课的内容,以帮助学生达到更好的学习效果。
(2)上课在上课过程中,教师可以先以一些圆锥曲线的简单例题来熟悉学生对波利亚解题理论的掌握情况。
然后,教师可以采用加深训练的方法,逐步增加难度,让学生用波利亚解题理论来解决更复杂的问题。
在教授方法时,教师可以详细讲解步骤,用不同的例子来让学生从多角度理解,并且与学生交流,加深学生对高三圆锥曲线的理解。
(3)总结在教学活动结束时,教师可以再次总结本节课的内容,提出一些细节问题,让学生对学过的知识有更深入的理解。
如果发现有学生对解题方法还存在困惑,教师应及时给予帮助,为学生解答问题,以提高学生自我学习能力。

波利亚的解题理论(讲稿)同学们好!今天我们大家一起来学习波利亚的解题理论。
首先,让我们了解一下波利亚的生平.乔治·波利亚(George Polya,1887-1985)美籍匈牙利数学家,生于匈牙利,青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、数学、物理和哲学,1912年获数学博士学位。
他是法国科学院、美国全国科学院和匈牙利科学院的院士,是20世纪举世公认的数学家和数学教育家,也是享有国际盛誉的数学方法论大师,为数学方法论的现代研究,特别是为数学解题教学研究奠定了必要的理论基础。
他的成就主要包括解题理论、数学教学理论和教师教育理论,发表200多篇论文和许多专著,主要著作包括:《怎样解题》(1944)、《数学的发现》(1954)、《数学与猜想》(1961)等。
其中《怎样解题》与《数学的发现》集中论述了怎样解题的问题,而《数学与猜想》则对合情推理进行了生动地、富有创造性地论述。
在数学方面,对实变函数、复变函数和概率论等若干分支领域作出了开创性的贡献,留下了以他的名字命名的术语和定理。
在数学解题研究领域,波利亚是一面旗帜,也是一代宗师。
这里主要介绍他的解题理论。
学习波利亚的解题理论,首先需要了解对“解题”过程的界定。
波利亚认为,解题是智力的特殊成就,题目是数学的心脏,数学教学的本质在于教会学生解题,解题思想“应当诞生在学生心里,教师仅仅像助产士那样行事"(苏格拉底语),由此,数学教师的首要任务是发展学生解决问题的能力.为了帮助学生,为了回答“一个好的解法是如何想出来的”这个令人困惑的问题,他专门研究可解题的思维过程,用朴素而现代化的形式来阐明探索法(既有助于发现的探索方法),并集几十年教学与科研之大成写成《怎样解题》一书,与1948年出版,风靡世界.其中“怎样解题"表仔细分析了求解各种数学问题时的思维过程,成为经典之作。
概括的说来,“怎样解题”表是波利亚的解题理论的核心内容。
![波利亚的《怎样解题》[word版]](https://uimg.taocdn.com/b81648d6162ded630b1c59eef8c75fbfc67d945e.webp)
波利亚的《怎样解题》[word版]乔治·波利亚是20世纪举世公认的数学家,著名的数学教育家,享有国际盛誉的数学方法论大师.波利亚在数学教育领域最突出的贡献是开辟了数学启发法研究的新领域,为数学方法论研究的现代复兴奠定了必要的理论基础。
波利亚致力于解题的研究,为了回答“一个好的解法是如何想出来的”这个令人困惑的问题,他专门研究了解题的思维过程,并把研究所得写成《怎样解题》一书。
这本书的核心是他分解解题的思维过程得到的一张《怎样解题表》。
波利亚的四步解题法:
1.彻底理解问题
2.形成解决思路
3.执行
4.总结
1、彻底理解问题:为了确保真正理解问题,你最好把问题用自已的话换成各种形式反复重新表达,但另忘了指出问题的主干:要求解的是什么?已知什么?要满足哪些条件?但凡能画图,一定要画出来。
2、形成解题思路:要专注,用过往经验,已撑握的知识,并调整适用性来形成思路。
如果不行,就改变这个问题的各个组件:已知、未知、条件,先构造简单一点的,引入辅助,条件是否用足,甚至改变求解的未知数,看能否找到解题线索?直到找到与之相似而你又解决过的问题。
3、执行:一要有耐心,二需要及时的检查每一步,可
凭直觉或证明(两个都有用,但是两回事),要问自已每一步都检查了吗?能看出来这一步是对的吗?能证明这一步是对的吗?
4、总结:巩固与提升的关键,多想想,再论证,尝试另外的解法,找更明快简捷的方法,还要问,这次的解法还能用在什么地方?总结是最好的启法时刻。

四个常用的解题模式波利亚
一、双轨迹模式
1.把问题归结为要确定一个‘点';
2.把条件分成两部分,使得对每一部分,未知点都在一轨迹上。
这两个轨迹
的‘交点'即所求。
二、笛卡尔模式
1.把问题归结为要确定若干个‘未知量';
2.设想问题已经解出,列出已知量和未知量之间根据条件必须满足的一切关
系式;
3.把某些关系式转化为方程,得出一个方程组;
4.把方程组通过消元化归为一个方程。
三、递归模式
1.设法将要求的量归结为某个依次排列的序列中的一项;
2.确定这序列中的第一项或前几项;
3.找出递推关系,将序列的一般项与前几项联系起来,从而可递推得到所求
项。
四、叠加模式
1.先处理一、两种特殊情形(称之为导引特款);
2.利用导引特款的叠加去得出一般问题的解。

浅谈波利亚解题理论对“怎样解题表”的认识乔治·波利亚(G.Polya,1887-1985年)出生于匈牙利布达佩斯。
上中学时,他就是一个很有上进心的学生。
但每当遇到较难的数学题时,他也时常感到困惑:“这个解答好像还行,它看起来是正确的,但怎样才能想到这样的解答呢?这个结论好像还行,它看起来是个事实,但别人是怎样发现这个事实的?我自己怎样才能想出或发现他们呢?”怎样解题表第一步:弄清问题第二步:拟订计划第三步:实现计划第四步:回顾我的认识与看法学习数学的目的,通常人们认为主要有两个,一是掌握必要的数学知识,二十提高分析的能力、解决问题的能力。
其中后者是数学教学的根本目标,但是,要有效的提高学生的分析和解决问题的能力却并非易事。
我认为乔治·波利亚有效地帮教师解决了这一难题。
但是要看教师个人怎样去用和实现这四部的教学法。
在我们看来这四个步骤十分的简单,但我们真的实施起来真的是那么回事吗?我想答案肯定是很难吧!下面我就这四步进行概括的说说我的看法。
①弄清问题,拟定计划这是解决数学问题的关键因素,探求解题思路的过程是训练学生良好思维方式的过程,也是教给学生恰当选取解题策略的过程。
在拟定计划中需要对问题不断地修正、转化,还经常需要类比等。
当我们引导学生将复杂问题转化为简单问题,把一个陌生的问题转化为熟悉的问题,这样一个解题的计划就基本形成了。
②回顾解答,深化理解这是巩固知识,提高解题能力的重要环节,在日常数学学习和活动中,我们往往在解答出某道题目后就立即进入另一个问题或找点别的事来干。
比利亚告诉我们:“没有任何一个题目是彻底完成了的……”。
所以当我们解决了一个问题后应该及时的进行反思,只有这样我们的解题水平才能得到有效的提高。
如果缺乏对问题本质的理解和更高层次的认识。
也失去了一个提高解题能力的好机会。
③小结应试教育,是中国平等待人的政治手法的灵活应用。
这样可以达到知识的普集和教育的平衡。
但是限制了学生的特长,使人从小养成了定向思维的习惯。

波利亚的解题理论一、波利亚的生平及主要著作对于我们数学学习者而言,大多都有过这样的经历:一道题,自己怎么想也想不出解法,而老师却给出了一个绝妙的解法。
这时候,我们最想知道“老师是怎么想出这个解法的”,如果这个解法不是很难,我们也许会问“自己完全可以想出,但为什么我没有想到呢?”要回答这个问题,实际上牵涉到对揭发数学问题解决规律的深入研究。
综观历史来看,美籍匈牙利数学家乔治。
波利亚(George Polya,1887-1985)不仅对上述问题特别感兴趣,而且在该领域做出了许多奠基性的工作。
波利亚是法国科学院,美国科学院和匈牙利科学院的院士,1887年出生在匈牙利,青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、物理和哲学,获博士学位。
1914年在苏黎世著名的瑞士联邦理工学院任教。
1940年移居美国,1942年起任美国斯坦福大学教授。
他一生发表200多篇论文和许多专著。
他在数学的广阔领域内有精深的造诣,对实变函数、复变函数、组合论、概率论、数论、几何等若干分支领域都做出了开创性的贡献,一些术语和定理都以他的命名。
由于他在数学教育方面所取得的成就和对世界数学教育所产生的影响,在他93岁高龄时,还被ICME(国际数学教育大会)聘为名誉主席。
《怎样解题》(1944),《数学的发展》(1945)和《数学与猜想》(1961)这三本书就是他智慧的结晶。
这些书被译成很多国家的文字出版,其中《怎样解题》一书被译成17种文字,仅平装本就销售了100万册以上。
著名数学家范。
德。
瓦尔登1952年2月2日在瑞士苏黎世大学的会议致辞中说:“每个大学生,每个学者,特别是每个老师都应该都读读这本引人入胜的书”。
这些书成了世界范围内的数学教育名著,对数学教育产生了深刻的影响。
二、波利亚对数学教育的基本看法波利亚对于数学教育的目的、价值、方法非常关注。
他认为,“中小学生到底为什么要学习数学?要学什么样的数学?通过什么途径学好数学?”具体一点就是,在中小学阶段,是以“学数学”为主呢,还是以学如何“用数学”为主呢?这一点必须弄清楚。

波利亚“怎样解题”的思想,内容及实践结果波利亚“怎样解题”的思想,内容及实践结果乔治.波利亚(George Polya) 1887年出生在匈牙利,青年时期曾在布达佩斯、维也纳、哥廷根,巴黎等地攻读数学、物理和哲学,获博士学位。
1914年在苏黎世著名的瑞士联邦理工学院任教。
1940年移居美国,1942年起任美国斯坦福大学教授。
他一生发表达200多篇论文和许多专著,他在数学的广阔领域内有精深的造诣,对实变函数、复变函数、概率论、数论、几何和微分方程等若干分支领域都做出了开创性的贡献,留下了以他的名字命名的术语和定理波利亚致力于解题的研究,为了回答“一个好的解法是如何想出来的”这个令人困惑的问题,他专门研究了解题的思维过程,并把研究所得写成《怎样解题》一书。
这本书的核心是他分解解题的思维过程得到的一张《怎样解题》表。
在这张包括“弄清问题”、“拟定计划”、“实现计划”和“回顾”四大步骤的解题全过程的解题表中,对第二步即“拟定计划”的分析是最为引人入胜的。
他指出寻找解法实际上就是“找出已知数与未知数之间的联系,如果找不出直接联系,你可能不得不考虑辅助问题。
最终得出一个求解计划。
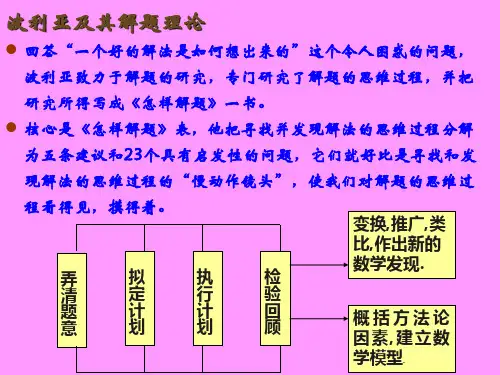
”他把寻找并发现解法的思维过程分解为五条建议和23个具有启发性的提示语,它们就好比是寻找和发现解法的思维过程的“慢动作镜头”,使我们对解题的思维过程看得见,摸得着。
波利亚的《怎样解题》表的精髓是启发你去联想。
联想什么?怎样联想?让我们看一看他在表中所提出的建议和提示性的问题吧。
“你以前见过它吗?你是否见过相同的问题而形式稍有不同?你是否知道与此有关的问题?你是否知道一个可能用得上的定理?看着未知数!试指出一个具有相同未知数或相似未知数的熟悉的问题。
这里有一个与你现在的问题有联系且早已解决的问题。
你能不能利用它?你能利用它的结果吗?你能利用它的方法吗?为了能利用它,你是否应该引入某些辅助元素?你能不能重新叙述这个问题?你能不能用不同的方式重新叙述它?┅ ┅”这些大量提示性的问题,不是问别人,而是问自己,实际是解题者的自我诘问,自我反省。
波利亚的解题理论一、波利亚的生平及主要著作对于我们数学学习者而言,大多都有过这样的经历:一道题,自己怎么想也想不出解法,而老师却给出了一个绝妙的解法。
这时候,我们最想知道“老师是怎么想出这个解法的”,如果这个解法不是很难,我们也许会问“自己完全可以想出,但为什么我没有想到呢?”要回答这个问题,实际上牵涉到对揭发数学问题解决规律的深入研究。
综观历史来看,美籍匈牙利数学家乔治。
波利亚(George Polya,1887-1985)不仅对上述问题特别感兴趣,而且在该领域做出了许多奠基性的工作。
波利亚是法国科学院,美国科学院和匈牙利科学院的院士,1887年出生在匈牙利,青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、物理和哲学,获博士学位。
1914年在苏黎世著名的瑞士联邦理工学院任教。
1940年移居美国,1942年起任美国斯坦福大学教授。
他一生发表200多篇论文和许多专著。
他在数学的广阔领域内有精深的造诣,对实变函数、复变函数、组合论、概率论、数论、几何等若干分支领域都做出了开创性的贡献,一些术语和定理都以他的命名。
由于他在数学教育方面所取得的成就和对世界数学教育所产生的影响,在他93岁高龄时,还被ICME(国际数学教育大会)聘为名誉主席。
《怎样解题》(1944),《数学的发展》(1945)和《数学与猜想》(1961)这三本书就是他智慧的结晶。
这些书被译成很多国家的文字出版,其中《怎样解题》一书被译成17种文字,仅平装本就销售了100万册以上。
著名数学家范。
德。
瓦尔登1952年2月2日在瑞士苏黎世大学的会议致辞中说:“每个大学生,每个学者,特别是每个老师都应该都读读这本引人入胜的书”。
这些书成了世界范围内的数学教育名著,对数学教育产生了深刻的影响。
二、波利亚对数学教育的基本看法波利亚对于数学教育的目的、价值、方法非常关注。
他认为,“中小学生到底为什么要学习数学?要学什么样的数学?通过什么途径学好数学?”具体一点就是,在中小学阶段,是以“学数学”为主呢,还是以学如何“用数学”为主呢?这一点必须弄清楚。
波利亚《怎样解题》波利亚(George Pólya)于1945年出版了一本名为《怎样解题》(How to Solve It)的书籍,这本书成为了解决问题的经典指南。
波利亚是一位知名的数学家,他在书中分享了他对问题解决过程的理解和方法。
《怎样解题》不仅适用于数学问题,也可以应用于各个领域。
解题的四个基本原则波利亚认为,解决问题有四个基本原则:理解问题、制定计划、执行计划和回顾。
下面将针对这四个原则进行详细讨论。
理解问题理解问题是解决问题的第一步。
对于有关问题的任何陈述,我们都需要理解其含义。
理解问题包括搞清楚问题的要求,识别问题中涉及到的关键数据和信息,并将问题进行分类。
分类问题可以帮助我们找出问题的模式和发现问题的规律。
在理解问题阶段,我们需要提出问题,并找出已知条件和未知数。
这个过程有助于我们建立解决问题的框架,并提供解决方案的线索。
制定计划在理解问题的基础上,我们需要制定一个解决问题的计划。
计划是解决问题的指导方针,可以帮助我们有条理地进行思考和行动。
制定计划的关键是找出解决问题的途径。
这可以通过思考类似的问题、试图将问题分解为更小的子问题以及利用问题中的条件和限制来实现。
制定计划时,我们还可以考虑使用图表、图形和模型来表示问题。
这有助于我们更好地理解问题,并找到解决问题的启示。
执行计划一旦我们制定了解决问题的计划,我们就要开始实施这个计划。
执行计划是解决问题的实质性步骤,需要我们运用适当的技能和方法。
在执行计划的过程中,我们要仔细记录和跟踪每一步骤,并确保以正确的方式执行。
如果在执行计划的过程中遇到问题,我们需要及时调整计划,找到新的方向。
回顾回顾是解决问题的最后一步。
在解决问题后,我们需要回顾整个解决过程,反思经验和教训,总结和归纳解决问题的方法和策略。
回顾过程可以帮助我们加深对问题解决过程的理解,并帮助我们提高解决问题的能力。
通过回顾,我们可以发现问题解决中的瑕疵和改进的空间,从而在下次面对类似问题时更好地应对。
波利亚解题理论如何拟定计划
波利亚教授提出的解题方法里,“拟定计划”这部分就像这样:
首先,你要把问题摸透——这就像是搞清楚故事的情节一样,得知道问题到底在问什么,有哪些已有的线索(也就是已知条件),我们要找的答案是什么(未知量)。
如果有图啊、示例啊,能帮你更好理解就别忘了利用起来。
接下来,脑筋动起来回忆一下学过的知识,想想哪些公式啦、法则啦、以前做过的题跟现在这个像不像?如果有类似的例子,那就太棒了,可以直接借鉴经验。
然后,试着把大难题拆分成几个小块儿,一块儿一块儿地啃总比一口吞容易。
就像是先解开一个小谜团,再接着下一个,最后串起来就是整个答案。
列个清单,把想到的各种解决办法都写下来,不怕多,就怕想不到。
有可能试试这个方法走不通,那就换种思路接着来,有点像探险家找寻宝藏时尝试各种路线。
最后,挑一个看着靠谱的方法,把它变成一步步的具体行动方案。
就像是画地图,标明每一步怎么走,走到哪算哪。
在动手之前,心里还得估摸估摸这个方案靠不靠谱,要是感觉不对劲,那就回头再修改修改。
所以呢,总的来说,拟定计划就是在充分理解问题的基础上,灵活运用知识,勇于尝试不同方法,并且步步为营地制定出一个实际可行的操作步骤。
波利亚四步解题法1. 什么是波利亚四步解题法?波利亚四步解题法(Polya’s Four-Step Problem Solving Method)是由匈牙利数学家乔治·波利亚(George Pólya)提出的一种解决问题的方法。
这个方法适用于各种领域的问题,包括数学、科学、工程等。
波利亚四步解题法的核心思想是通过有序、系统的方式来解决问题,以确保每个步骤都得到适当的考虑和分析。
这种方法强调了问题解决过程中的创造性思维和灵活性,而不仅仅是机械地应用公式和算法。
2. 波利亚四步解题法的四个步骤2.1 理解问题(Understand the problem)在解决任何问题之前,首先需要全面理解问题的要求和限制。
这包括明确问题所涉及的概念、条件和目标。
在这一步骤中,可以通过以下几个方面来帮助理解问题:•仔细阅读问题陈述,并将其转化为自己理解的语言。
•将关键信息提取出来,并进行归纳总结。
•确定问题的目标和要求,明确需要解决的具体内容。
理解问题的过程中,可以使用思维导图、流程图等工具来帮助整理和梳理思路。
2.2 制定计划(Devise a plan)在理解问题之后,接下来需要制定解决问题的计划。
这个步骤是一个关键的思考过程,它要求我们考虑使用哪些方法、公式或算法来解决问题。
以下是一些常见的解题策略:•找出类似的问题,并尝试将其应用到当前问题上。
•将大问题分解为小问题,并逐一解决。
•使用图表、模型或示意图来帮助理清思路。
制定计划时,可以尝试不同的方法和角度,寻找最适合自己的解题策略。
2.3 执行计划(Carry out the plan)在制定好计划之后,就可以开始执行计划了。
这一步骤是具体操作和计算的过程。
根据制定的计划,按照一步一步地进行操作,直到得出最终结果。
在执行计划时,需要注意以下几点:•确保每个步骤都正确无误地执行。
•保持记录和注释,以便追溯和复查。
•尝试不同的方法和技巧,以获得更好的结果。
波利亚的解题理论一、波利亚的生平及主要著作对于我们数学学习者而言,大多都有过这样的经历:一道题,自己怎么想也想不出解法,而老师却给出了一个绝妙的解法。
这时候,我们最想知道“老师是怎么想出这个解法的”,如果这个解法不是很难,我们也许会问“自己完全可以想出,但为什么我没有想到呢?”要回答这个问题,实际上牵涉到对揭发数学问题解决规律的深入研究。
综观历史来看,美籍匈牙利数学家乔治。
波利亚(George Polya,1887-1985)不仅对上述问题特别感兴趣,而且在该领域做出了许多奠基性的工作。
波利亚是法国科学院,美国科学院和匈牙利科学院的院士,1887年出生在匈牙利,青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、物理和哲学,获博士学位。
1914年在苏黎世著名的瑞士联邦理工学院任教。
1940年移居美国,1942年起任美国斯坦福大学教授。
他一生发表200多篇论文和许多专著。
他在数学的广阔领域内有精深的造诣,对实变函数、复变函数、组合论、概率论、数论、几何等若干分支领域都做出了开创性的贡献,一些术语和定理都以他的命名。
由于他在数学教育方面所取得的成就和对世界数学教育所产生的影响,在他93岁高龄时,还被ICME(国际数学教育大会)聘为名誉主席。
《怎样解题》(1944),《数学的发展》(1945)和《数学与猜想》(1961)这三本书就是他智慧的结晶。
这些书被译成很多国家的文字出版,其中《怎样解题》一书被译成17种文字,仅平装本就销售了100万册以上。
著名数学家范。
德。
瓦尔登1952年2月2日在瑞士苏黎世大学的会议致辞中说:“每个大学生,每个学者,特别是每个老师都应该都读读这本引人入胜的书”。
这些书成了世界范围内的数学教育名著,对数学教育产生了深刻的影响。
二、波利亚对数学教育的基本看法波利亚对于数学教育的目的、价值、方法非常关注。
他认为,“中小学生到底为什么要学习数学?要学什么样的数学?通过什么途径学好数学?”具体一点就是,在中小学阶段,是以“学数学”为主呢,还是以学如何“用数学”为主呢?这一点必须弄清楚。