当前位置：文档之家 › 02 晶体的弹性

02 晶体的弹性

  • 格式：pdf
  • 大小：524.05 KB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

Chap11.晶体物理学基础

Chap11.晶体物理学基础

晶体学
对于二阶和四阶张量,都是中心对称的,用张量 描述的物理性质也是中心对称的.即具有对称中 描述的物理性质也是中心对称的.即具有对称中 心的晶体也存在有二阶张量和四阶张量所描述的 物理性质. 对于三阶张量,它的变换定律为 d′ijk=ailaimakndlmn, 代入 ail= ajm= akn=-1,则 d′ijk=-dijk.因为是对称变 换,故变换前后的对应分量相等,因此,d 换,故变换前后的对应分量相等,因此,dijk的全 部分量为零.也就是说,具有对称中心的晶体不 部分量为零.也就是说,具有对称中心的晶体不 存在由三阶张量所描述的物理性质. 综上所述,凡具有对称中心的晶体,都不存在由 综上所述,凡具有对称中心的晶体,都不存在由 奇阶张量所描述的物理性质,但对偶阶张量都不 施加额外的影响.
晶体学 例如:在均匀导体中,在电场强度E的作用下,其电流 例如:在均匀导体中,在电场强度E的作用下, 密度J 有相同的方向, 的大小与E的大小成正比, 密度J与E有相同的方向,而J的大小与E的大小成正比, 这就是欧姆定律. 这就是欧姆定律. 表示成分量形式:Ji= σEi ,i=1, 2, 3;此处σ 称为电导率, 表示成分量形式: 3;此处σ 称为电导率, 为标量. 为标量. 对于晶体,晶体具有各向异性,一般情况下电流密度J与 对于晶体,晶体具有各向异性,一般情况下电流密度J 电场强度E不具有相同的方向. 电场强度E不具有相同的方向.
张量远比标量和矢量复杂,它的每一个分量将与 张量远比标量和矢量复杂, 两个或三个以上的方向有关, 两个或三个以上的方向有关,而且在坐标系变换 时,必须根据一定的变换定律进行变换. 必须根据一定的变换定律进行变换.
材料科学与工程学院( 材料科学与工程学院(School of science materials & technology)

弹性与弹性变形

弹性与弹性变形

σ 13 ⎞ ⎟ σ 23 ⎟ σ 33 ⎟ ⎠
σ ij = σ ji
受力状态－由应力张量确定任意方向面上应力分量的方法
问题：立方系单晶体受力问题，通常取<100>方向为坐标 轴方向。已知应力张量，如何确定各“滑移系”的应力？ 承载面法向的单位方向矢量： 承载面切向的单位方向矢量：
no = (cos α1 , cos α 2 , cos α 3 )
1.1 受力与变形状态的表达
载荷P：承载面上的总作用力 【N】 应力矢量F ：单位面积上承受的载荷 F= P /A 【MPa, 1MPa=106 N/m2】 直角坐标系下，立方 体面上的应力分量
σ ij =
dPij dAi
应力张量： 其中：
⎛ σ 11 σ 12 ⎜ σ = ⎜ σ 21 σ 22 ⎜σ ⎝ 31 σ 32
应力应变张量各有6个“有效”值 胡克定律可简化为：
⋅ ⋅ S16 ⎞ ⎛σ1 ⎞ ⎛ ε1 ⎞ ⎛ S11 S12 ⋅ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⋅ ⎟ ⎜σ2 ⎟ ⎜ε 2 ⎟ ⎜ S21 ⋅ ⎜ε ⎟ ⎜ ⋅ ⋅ ⎟ ⎜σ3 ⎟ S33 3 ⎜ ⎟ =⎜ ⎟⋅⎜ ⎟ ⋅ ⎟ ⎜σ4 ⎟ S44 ⎜ε 4 ⎟ ⎜ ⋅ ⎜ε ⎟ ⎜ ⋅ ⋅ ⋅ ⎟ ⎜σ5 ⎟ ⎜ 5⎟ ⎜ ⎟⎜ ⎟ ⎜ε ⎟ ⎜ S ⋅ ⋅ ⋅ S66 ⎟ ⎜σ6 ⎟ ⎝ 6 ⎠ ⎝ 61 ⋅ ⎠⎝ ⎠
应变：
工程应变ε/真应变εt 工程正应变 真应变
Δl ε = l0
dl dε t = l
σ t = σ (1 + ε )
l 关系：ε t = ln = ln(1 + ε ) l0
回答相关问题时，注意区分，不要模糊！
练习题：在晶轴坐标系下，写出(001)面承受200MPa压应力 的立方单晶体的应力张量，计算(111)[-110]滑移系的分切应 力值。如果同时在（010）面上还承受100MPa的拉应力， 应力张量如何？滑移系的分切应力为多少？

《固体物理学》房晓勇主编教材-习题解答参考02第二章_晶体的结合和弹性

《固体物理学》房晓勇主编教材-习题解答参考02第二章_晶体的结合和弹性

d 2U ( dV 2 )V0
=
1 9V 2
0
⋅
N 2
⎡ ⎢ ⎣
−
m2 A r0m
+
n2B ⎤
r0n
⎥ ⎦
=
1 9V02
⋅
N 2
⎡⎢−m ⎣
mA r0m
+
n
nB r0n
⎤ ⎥ ⎦
=
1 9V02
⋅
N 2
⎡⎢−m ⎣
nB r0n
+
n
mA ⎤
r0m
⎥ ⎦
=
−
mn 9V02
⋅
N 2
⎡⎢− ⎣
A r0m
+
B r0n
第二章 晶体的结合和弹性 第二章 晶体的结合和弹性
2.1 有一晶体，在平衡时的体积为V0 ，原子之间总的相互作用能为U0 ，如果相距为 r 的原子间相互作用能
由下式给出： 证明：（1）体积弹性模量为
u(r) = − A + B ， rm rn
K
=
U0
mn 9V0
（2）求出体心立方结构惰性分子晶体的体积弹性模量。 解：参考王矜奉 2.2.1 根据弹性模量的定义可知
2
平衡条件
dU dr
|r = r0
=
⎛ ⎜⎜⎝
mA r m+1
0
−
nB r n+1
0
⎞ ⎟⎟⎠
=
0
得
mA r m+1
0
=
nB r n+1
0
第二章 晶体的结合和弹性
1
r0
=
⎛ ⎜⎝
nB mA
⎞n−m ⎟⎠

晶体跟非晶体的名词解释

晶体跟非晶体的名词解释

晶体跟非晶体的名词解释晶体与非晶体：隐藏在物质世界中的奇妙结构在我们周围的物质世界中，晶体和非晶体这两个名词经常被提及，相信大家对它们都有一定的了解。

本文将从晶体和非晶体的基本概念入手，探讨它们的结构、性质以及在我们日常生活中的重要应用。

一、晶体的奇妙结构与性质晶体是由具有一定的周期性重复排列的粒子组成的固体。

其中，晶体的排列具有规律性，呈现出独特的几何形态和细致的晶格结构。

这种规律性排列导致了晶体的许多独特性质。

1. 晶体的透明性：大部分晶体都具有良好的透明性，因为它们粒子间的周期性排列使得光线可以穿过晶体而不发生散射。

例如，钻石就是一种透明的晶体，因为它的碳原子以六角形的晶格排列。

2. 晶体的硬度：晶体的排列结构赋予它们出色的硬度。

其中，金刚石是最硬的物质，这是由于它在晶格中的碳原子之间形成了非常强大的共价键。

这种硬度使得金刚石成为珠宝和工具制造领域的重要材料。

3. 晶体的熔点：晶体具有明确的熔点，当温度升高到晶体的熔点时，晶体开始熔化成液体。

这是由于晶体内部粒子的排列结构在加热过程中发生了破坏。

4. 晶体的电学性质：晶体可以表现出丰富的电学性质，如导电性、压电效应和光电效应等。

这些性质与晶体内部粒子的排列方式密切相关。

例如，硅晶体由硅原子排列而成，因此被广泛用于制造电子器件。

二、非晶体：无规则中的秩序与晶体相对应的是非晶体，也被称为无定形固体。

它的结构特点是粒子排列的无规则性，缺乏明确的晶格结构。

非晶体的形成往往是由于材料快速冷却或者化学成分的复杂性。

1. 非晶体的弹性：与晶体相比，非晶体的结构比较松散，因此具有较低的硬度。

然而，非晶体材料的弹性却相对较好。

例如，玻璃就是一种非晶体材料，其具有良好的弹性特性，广泛用于制造容器、建筑装饰和光学器件等。

2. 非晶体的导电性：通常情况下，非晶体的导电性较差，因为其中没有规律的结构可以促进电子在材料中的流动。

然而，一些特殊的非晶体材料如氢化非晶硅则具有良好的半导体性质，被广泛应用于光伏和显示技术领域。

第六章 多晶体的塑性变形

第六章 多晶体的塑性变形

强化手段，可提高材料抗突然超载的能力。
意义：
1）是一种材料强化手段—形变强化；
2）有利于塑性变形均匀进行； 3）有利于金属构件的工作安全性。
28
3.加工硬化的不利
1）影响材料力学性能
不利：使得再变形困难；
使得金属的切削加工，冲压加工带来困难。 解决办法： 在冷加工之间进行中间热处理——再结晶退火。 2）影响材料物理性能和化学性能 不利：电阻增加，导电、导磁性下降； 化学活性增大；耐腐蚀性下降。
b
式中：
Fb S0
MP a
Fb— 指试样被拉断前所承受的最大外力， 即拉伸曲线上b点所对应的外力（N）。 S0 — 试样原始横截面面积（mm2）
37
二、塑性指标（ δ%；Ψ %）
定义： 塑性—材料受力后在断裂之前产生塑性变形的能力。 (1)断后伸长率
公式： δ% = （Lu- L0）/L0 ×100%
自由锻
模锻
19
5）冷冲压
（低碳钢、合金钢板材）
20
一、塑性变形的基本概念
1.载荷
（1）定义
金属材料在加工及使用过程中所受的外力。
（2）类型
根据载荷作用性质不同：
a）静载荷 b）动载荷 —没有变化； —瞬间变化；
c）交变载荷—不断变化。
21
根据载荷作用性质不同：
a）拉深载荷 --拉力
b）压缩载荷 —压力
塑性变形前 塑性变形后
3、形变织构产生
金属塑性变形到很大程度(70%以上)时, 由于晶粒发生转动, 使各晶粒的位向 趋近于一致, 形成特殊的择优取向, 这种有序化的结构叫做形变织构。
6.4.2. 塑性变形对金属性能的影响
• （1）形变强化 金属发生塑性变形, 随变形度的增大, 金属 的强度和硬度显著提高, 塑性和韧性明显下降。 • （2）产生各向异性 由于纤维组织和形变织构的形成, 使 金属的性能产生各向异性。

固体物理学：第三章晶体结合及弹性模量n

固体物理学：第三章晶体结合及弹性模量n

第三章晶体的结合、弹性模量•3.1 晶体中的结合力和结合能；•3.2 元素和化合物晶体结合的规律性；•3.3 弹性应变和晶体中的弹性波；3.1 晶体的结合力和结合能一. 晶体结合的一般概念：自然界的矿物中绝大多数物质都以晶态存在，说明晶体的能量比构成晶体的粒子处在自由状态时的能量总和要低的多,因此可以给出U0是晶体在0K 时的总能量，E N是N个自由粒子能量之和，因此Eb 是0K时把晶体分解为相距无限远、静止的中性自由原子所需要的能量，称作内聚能（Cohesive energy）或结合能（binding energy)。

取EN＝0，做能量基点，则有：近似把原子对间相互作用能量之和当作晶体的总相互作用能。

物质以晶态存在是由于构成固体的原子之间存在着相当大的相互作用力，尽管不同晶体这种结合力的类型和大小不同，但两个粒子之间相互作用力（势）与它们间距离的关系在定性上是相同的。

晶体中粒子的相互作用可以分为2大类：斥力和引力。

晶态是粒子间斥力、引力处于平衡时的状态。

其中a 、b 、m 、n 均为大于零的常数，由实验确定若两粒子要稳定结合在一起，则必须满足n > m一对粒子之间的相互作用势一般可以表示为引力势和斥力势之和:处于稳定态的条件是：给出平衡位置:平衡时的能量：★从上式可以看出晶体有平衡态的条件是：n > m★更符合实际斥力势变化规律的表达式为指数形式：N个原子组成晶体后的总相互作用能，忽略边界的差异，可以近似表示为：二. 晶体的弹性性质：以晶体相互作用能来解释晶体弹性性质是对理论表达式正确与否的最好验证。

1. 压缩系数η与体弹性模量K ：由热力学知道：考虑到：两式相比较，有：展开式中的第一项在平衡点为零。

注解：体积弹性模量：按胡克定律，在弹性限度内，物体形变产生的内应力与相对形变成正比，比例系数称弹性模量。

由热力学第一定律dU=TdS–pdV，若不考虑热效应，即TdS= 0 （实际上只有当T=0K时才严格成立），有2. 抗张强度：晶体所能负荷的最大张力叫抗张强度，负荷超过抗张强度时，晶体就会断裂。

高分子物理考研习题整理02高分子的聚集态结构

高分子物理考研习题整理02高分子的聚集态结构1 高分子结晶的形态①指出聚合物结晶形态的主要类型, 并简要叙述其形成条件有五种典型的结晶形态。

单晶: 只能从极稀的聚合物溶液中缓慢结晶得到。

球晶: 从浓溶液或熔融体冷却时得到。

伸直链晶体: 极高压力（通常需几千大气压以上）下缓慢结晶。

纤维状晶体：受剪切应力（如搅拌）, 应力不足以形成伸直链片晶时得到。

串晶: 受剪切应力（如搅拌）, 后又停止剪切应力时得到。

②让聚乙烯在下列条件下缓慢结晶, 各生成什么样的晶体？（1）从极稀溶液中缓慢结晶；（2）从熔体中结晶；（3）极高压力下结晶；（4）在溶液中强烈搅拌结晶（1）从极稀溶液中缓慢结晶, 得到的是单晶。

1957年Keller在极稀溶液中, 于Tm附近缓慢地冷却或滴加沉淀剂使聚乙烯结晶, 得到菱形的聚乙烯折叠链的单晶。

（2）从熔体中结晶, 得到的是球晶, 球晶的基本单元仍是折叠链晶片。

（3）极高压力下结晶, 得到的是伸直链晶体。

例如, 聚乙烯在226℃、4800atm下结晶8h, 得到完全伸直链的晶体, 其熔点由原来的137℃提高的140.1℃, 接近平衡熔点144℃。

（4）在溶液中强烈搅拌结晶, 得到的是串晶。

因为搅拌相当于剪切应力的作用, 使结晶与取向同时进行。

串晶由两部分组成, 中间为伸直链的脊纤维i, 周围是折叠链晶片形成的附晶。

由于结晶是在分子链的主链上成核, 在垂直方向上长大, 因此得到的是串晶。

③聚合物因结晶方法、热处理和力学处理不同, 呈现出不同的结晶形态, 简述下列各种形态结构的特征。

（1）单晶（2）球晶（3）拉伸纤维晶（4）非折叠的伸直链晶体（5）串晶（1）单晶: 厚为10-50nm的薄板状晶体（片晶）, 有菱形、平行四边形、长方形、六角形等形状, 分子链呈折叠链构象, 分子链垂直于片晶表面；（2）球晶: 球形或截顶的球晶, 由折叠链片晶从中心往外辐射生长组成；（3）拉伸纤维晶: 纤维状晶体中分子链完全伸展, 但参差不齐, 分子链总长度大大超过分子链平均长度；（4）非折叠的伸直链晶体：厚度与分子链长度相当的片状晶体, 分子链呈伸直链构象；（5）串晶：以纤维状晶作为脊纤维, 上面附加生长许多折叠链片晶。

原子结构和晶体结构的力学稳定性分析

原子结构和晶体结构的力学稳定性分析导言：原子结构和晶体结构的力学稳定性是材料科学和工程领域中的重要研究课题。

在材料设计和制备过程中，了解材料的力学稳定性对于材料的性能和可靠性具有重要意义。

本文将从原子结构和晶体结构两个方面，探讨材料的力学稳定性分析。

一、原子结构的力学稳定性分析原子是材料的基本组成单位，其结构对材料的性能和力学稳定性起着决定性的作用。

原子结构的力学稳定性分析主要包括原子间的键合强度和晶格畸变的影响。

1. 原子间的键合强度原子间的键合强度决定了材料的力学性能和稳定性。

常见的键合类型包括共价键、离子键和金属键。

共价键的力学稳定性取决于原子之间的电子共享程度和键长，离子键的力学稳定性取决于正负离子之间的电荷差异和离子半径，金属键的力学稳定性取决于金属原子之间的电子云重叠程度和金属键的数量。

通过计算原子间的键能和键长，可以评估材料的力学稳定性。

2. 晶格畸变的影响晶格畸变是指晶体结构中原子位置的微小偏移。

晶格畸变的出现可能导致晶体结构的不稳定性，从而影响材料的力学性能。

晶格畸变可以通过实验观察晶体的衍射图案或通过计算方法进行分析。

通过研究晶格畸变的形成机制和对材料性能的影响，可以提高材料的力学稳定性。

二、晶体结构的力学稳定性分析晶体结构是由原子或分子按照一定的规则排列而成的有序固体。

晶体结构的力学稳定性分析主要包括晶体的弹性性质和晶体的缺陷对力学稳定性的影响。

1. 晶体的弹性性质晶体的弹性性质是指晶体在外力作用下发生弹性变形的能力。

晶体的弹性性质可以通过弹性常数来描述，包括弹性模量、剪切模量和泊松比等。

通过实验测量晶体的弹性常数，可以评估晶体的力学稳定性和弹性变形的能力。

2. 晶体的缺陷对力学稳定性的影响晶体中存在各种缺陷，如点缺陷、线缺陷和面缺陷等。

这些缺陷对晶体的力学稳定性和性能有着重要影响。

例如，点缺陷可以导致晶体的塑性变形和断裂，线缺陷可以影响晶体的强度和断裂韧性，面缺陷可以导致晶体的晶界强化和断裂韧性的提高。

固体物理学基础晶体的弹性性质与弹性波

固体物理学基础晶体的弹性性质与弹性波晶体是固体物质中的一种特殊结构，它具有高度有序的排列方式和周期性的结构。

在固体物理学中，研究晶体的弹性性质和弹性波是一项重要的课题。

本文将从晶体的弹性性质和弹性波的特性两个方面介绍和讨论。

一、晶体的弹性性质晶体的弹性性质是指晶体在外力作用下发生形变后，恢复到原始状态的能力。

晶体的弹性性质与普通物质有所不同，主要体现在以下几个方面：1. 弹性模量弹性模量是衡量晶体材料抵抗形变的能力的物理量。

对于各向同性晶体，常用的弹性模量有四个，分别是杨氏模量、泊松比、剪切模量和弹性体积模量。

杨氏模量描述了晶体在应力作用下产生的弹性应变和应力之间的关系；泊松比表示晶体在一方向上受到压缩时，在垂直方向上的膨胀程度；剪切模量衡量晶体抵抗剪切形变的能力；弹性体积模量表示晶体受到体积变化时的抵抗能力。

2. 晶体的弹性各向异性晶体具有各向异性，即晶体沿不同晶向具有不同的力学性质。

这是由于晶体内原子或离子的排列方式决定的。

晶体的各向异性体现在弹性模量、声速等物理性质上。

3. 弹性畸变晶体中存在着各种各样的缺陷和畸变，如晶格缺陷、位错、晶界等。

这些缺陷和畸变会对晶体的弹性性质产生影响，使晶体的弹性模量发生变化。

二、弹性波的特性弹性波是指在弹性介质中传播的一种机械波。

晶体中的弹性波可以分为纵波和横波两种类型：1. 纵波纵波是沿着波的传播方向，介质中的质点作径向的振动。

在晶体中，纵波的传播速度由杨氏模量和密度决定。

2. 横波横波是晶体中的质点在垂直于波的传播方向上作振动。

与纵波不同，晶体中的横波不能沿所有晶向传播，而只能沿一些特定的晶向传播。

3. 声速声速是弹性波在介质中的传播速度，是衡量介质中弹性性质的重要参数。

在晶体中，声速与晶体的密度、弹性模量和各向异性有关。

三、应用和研究进展晶体的弹性性质和弹性波在材料科学、地球物理学、电子学等领域具有重要的应用价值和研究意义。

例如，在材料科学中，通过研究晶体的弹性性质，可以评估材料的机械性能和可塑性；在地球物理学中，利用弹性波可以研究地球的内部结构和地震等现象；在电子学领域，晶体的弹性性质对电子器件的性能和稳定性影响巨大。

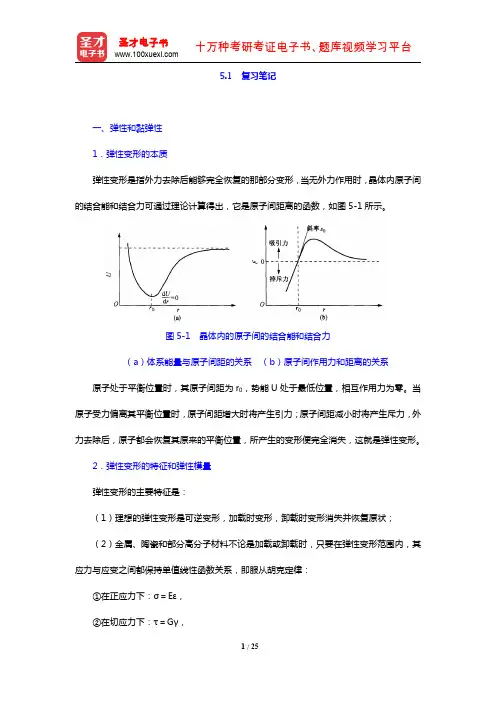
胡赓祥《材料科学基础》(第3版)(复习笔记 材料的形变和再结晶)【圣才出品】

5.1复习笔记一、弹性和黏弹性1．弹性变形的本质弹性变形是指外力去除后能够完全恢复的那部分变形，当无外力作用时，晶体内原子间的结合能和结合力可通过理论计算得出，它是原子间距离的函数，如图5-1所示。

图5-1晶体内的原子间的结合能和结合力（a）体系能量与原子间距的关系（b）原子间作用力和距离的关系原子处于平衡位置时，其原子间距为r0，势能U处于最低位置，相互作用力为零。

当原子受力偏离其平衡位置时，原子间距增大时将产生引力；原子间距减小时将产生斥力，外力去除后，原子都会恢复其原来的平衡位置，所产生的变形便完全消失，这就是弹性变形。

2．弹性变形的特征和弹性模量弹性变形的主要特征是：（1）理想的弹性变形是可逆变形，加载时变形，卸载时变形消失并恢复原状；（2）金属、陶瓷和部分高分子材料不论是加载或卸载时，只要在弹性变形范围内，其应力与应变之间都保持单值线性函数关系，即服从胡克定律：①在正应力下：σ＝Eε，②在切应力下：τ＝Gγ，弹性模量与切变弹性模量之间的关系为：式中，υ为材料泊松比，表示侧向收缩能力，在拉伸试验时系指材料横向收缩率与纵向伸长率的比值。

弹性模量代表着使原子离开平衡位置的难易程度，反映原子间结合力，是表征晶体中原子间结合力强弱的物理量。

（3）弹性的不完整性①包申格效应材料经预先加载产生少量塑性变形，而后同向加载则σe升高，反向加载则σe下降。

②弹性后效在弹性极限范围内，应变滞后于外加应力，并和时间有关的现象称为弹性后效或滞弹性。

③弹性滞后由于应变落后于应力，在σ-ε曲线上使加载线与卸载线不重合而形成一封闭回线，称之为弹性滞后，如图5-2所示。

图5-2弹性滞后（环）与循环韧性（a）单向加载弹性滞后（环）（b）交变加载（加载速度慢）弹性滞后（c）交变加载（加载速度快）弹性滞后（d）交变加载塑性滞后（环）④黏弹性黏弹性变形既与时间有关，又具有可回复的弹性变形性质，即具有弹性和黏性变形两方面的特征。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.1 位移与应变张量（10）
因为
dX1′
=
dX1
+
du1
=
dX1
+
∂u1 ∂X1
dX1
+
∂u1 ∂X 2
dX 2
+
∂u1 ∂X3
dX3
⎫ ⎪ ⎪
dX
′
2
=
dX 2
+
du 2
=
dX 2
+
∂u 2 ∂X1
dX1
+
∂u 2 ∂X 2
dX 2
+
∂u 2 ∂X3
⎪ dX3 ⎬
⎪
dX
′
3
=
dX3
+
du 3
=
dX2 B
当晶体发生形变时，质点在平面内均产
θ12
D
生了位移，而且各质点的位移一般是不 A是的u向同向1'+C发的A的位d''相uB生。位移1'的相对如u移，2对位+A果，BdC点A我移那u发B2变们，么的发生到只C位A生了点B点考移了一’变处变查。θ个到，到沿显1θ2C沿AX的然2'‘11处X点方角的，1，方发向角度总沿和生向度变的XXu发变化效122,化方方，果生u2。
⎤ )⎥ ⎥
1 2
( ∂u2 ∂X3
+
∂u 3 ∂X 2
⎥ )⎥ ⎥
∂u 3 ∂X3
⎥ ⎥ ⎦
2.1 位移与应变张量（12）
其中
η11
=
∂u1 ∂X1
η22
=
∂u 2 ∂X 2
η33
=
∂u 3 ∂X3
⎫ ⎪ ⎪
η23
= η32
=
1 2
( ∂u2 ∂X3
+
∂u 3 ∂X 2
)
η31
= η13
=
1 2
( ∂u1 ∂X3
+
∂u3 ) ∂X1
η12
= η21
=
1（ ∂u1 2 ∂X2
+
∂u2 ) ∂X1
⎪ ⎪⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪⎭
比较位移梯度矩阵与应变张量矩阵，发现两者有如下联系：
η = 1 (E + E′) = 1 (∇u + ∇u′)
2
2
式中的E'表E的转置，▽u'表示▽u的转置。此式告诉我们，
第二章 晶体的弹性
晶体在外力作用下，一般发生两种变化：一种是位置的 变化,包括刚性平移和转动，另一种是形变，包括体积和形状 的变化，亦即质点相对位置的变化。晶体发生形变的同时， 在晶体中将产生与形变有关的内力。通常描述形变用应变张 量，描述内力用应力张量。
晶体的弹性是指外力撤除后，晶体能消除形变恢复原状 的性质。这种能恢复的形变称弹性形变。每种晶体都具有一 定的弹性限度，在弹性限度内，晶体可以看成是一个弹性体。 由于晶体是各向异性体，描述晶体弹性性质的物理量为张量。
相对根伸据缩应量变；分η量2η为1X,η2方2,η向3上与的位相移对的伸关缩系量式；，η不3难为看X3出方，向η上1的为相X1对方伸向缩上量的。
为 了 说 明 应 变 分 量 η4,η5,η6 的 物 理意义，我们在晶体的一个平面上取相
X2
du1
D'
邻近的三个质点A、B、C，选取坐标
B'
系 相
距，为使d该X平2，面A为、XC3两面质。点令相A、距B为两dX质1点。
+ +
∂u 3 ∂X1
)
⎤ ⎥ ⎥
∂u 3 ∂X 2
⎥ )⎥ ⎥
⎡dX1 ⎤ ⎢⎥
⎢⎥
×
⎢⎢dX2
⎥ ⎥
∂u 3 ∂X3
⎥⎢ ⎥
⎥ ⎦
⎢⎣dX3 ⎥⎦
式中的二阶对称矩阵即为描述形变的应变张量。用η表示应
变张量矩阵，则有
⎡η11 η12 η = ⎢⎢η21 η22
⎢⎣η31 η32
η13 ⎤
η23
⎥ ⎥
由于P点的任意性，u((X1，X2，X3,t)是描述晶体中所有质点 的位移参量。
在一般情况下，位移矢量可由刚性运动和形变两部分产 生。晶体不存在形变，只存在刚性运动时，质点仍产生位 移，因此位移矢量与形变没有必然的联系，不能用来描述 晶体的形变。
2.1 位移与应变张量（4）
我们再考察P点附近的任
意 点 Q 的 坐 标 为 (X1+dX1 ， X2+dX2 ， X3+dX3) ， 其 位 置 矢 量 为 L+dL 。在同样外力作用
当晶体的位移梯度矩阵为零时，应变张量必定为零，此时无
形变。
2.1 位移与应变张量（13）
因为应变分量只有六个是独立的，因此可以用简缩下标 表示应变分量。其对应关系为：
η1 = η11
⎫
η2 = η22
⎪ ⎪
η3 = η33 η4 = 2η23 = 2η32
⎪⎪ ⎬ ⎪
η5 = 2η13 = 2η31
⎤ ⎥ ⎥ ⎥⎦
=
⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
∂u1
∂X1 ∂u 2
∂X1 ∂u 3
∂u1
∂X 2 ∂u 2
∂X 2 ∂u 3
∂u1
∂X3 ∂u 2
∂X3 ∂u 3
⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥
⎡ dX1 ⎢⎢dX 2 ⎢⎣dX3
⎤ ⎥ ⎥ ⎥⎦
⎢⎣ ∂X1 ∂X2 ∂X3 ⎥⎦
即
du i
=
∂u i ∂X j
+
2
∂u 2 ∂X 2
dX 2 2
+
2
∂u 3 ∂X3
dX32
+
2( ∂u1 ∂X 2
+
∂u 2 ∂X1
)dX1dX 2
+
2( ∂u2 ∂X3
+
∂u 3 ∂X 2
)dX 2 dX 3
+
2( ∂u3 ∂X1
+
∂u1 ∂X3
)dX1dX3
2.1 位移与应变张量（11）
将上式写成矩阵形式
⎡ ⎢ ⎢
∂u1 ∂X1
⎢ ⎢
∂X1
⎢ ⎢
0
⎢
⎢ ⎢0
∇s
=
⎢ ⎢
⎢0
⎢
⎢∂
→
则 η = ∇s u
⎢ ⎢
∂X
3
⎢∂
⎢
此式反映应变张量与位移矢量的关系。 ⎣∂X2
0
0
⎤ ⎥
⎥
∂
⎥
∂X 2
0⎥ ⎥
∂⎥
0
∂X 3
⎥ ⎥
∂
∂⎥
∂X 3
∂X 2
⎥ ⎥
∂⎥
0
∂X 1
⎥ ⎥
∂
⎥
∂X 1
0⎥ ⎦
2.1 位移与应变张量（16）
三、应变分量的物理意义
X
′
1
=
X1′ (X1, X 2 , X3 )
X
′
2
=
X
′
2
(X1
,
X
2
,
X
3
)
X
′
3
=X
′
3
(X1
,
X
2
,
X
3
)
即p‘点的位置矢量以及p点的位置矢量均可以表示为(X1， X2，X3)的函数。
2.1 位移与应变张量（3）
另外L又是时间t的函数，所以位移矢量也是坐标和时 间的函数，表示为
→
→
→
u(X1, X2 , X3, t) = L′(X1, X2 ,X3, t) - L(X1, X2 , X3, t)
Δ = 2[dX1
dX 2
dX
3
]
×
⎢ ⎢ ⎢
1 2
( ∂u1 ∂X 2
+
∂u 2 ∂X1
)
⎢1 ⎢ ⎣2
( ∂u1 ∂X3
+
∂u 3 ∂X1
)
1 ( ∂u1 + ∂u2 ) 2 ∂X2 ∂X1 ∂u 2 ∂X 2 1 ( ∂u2 + ∂u3 ) 2 ∂X3 ∂X2
1 2 1 2
( ∂u1 ∂X3 ( ∂u2 ∂X3
第二章 晶体的弹性
位移与应变张量 应力矢量和应力张量 晶体中质点的平移运动方程 虎克定律
2.1 位移与应变张量（1）
一、位移与位移梯度
晶体在外力作用下，将可发 A'
生刚性平移、转动以及质点相
A
对位移，从而使晶体由A变到A'
如图所示，图中虚线上的格点
表示质点的初始位置，实线上
格点表示发生位移后的终止位
∂u 1 ∂X1 ∂u 2 ∂X 2 ∂u 3 ∂X3 ∂u2 + ∂u3 ∂X3 ∂X2 ∂u1 + ∂u3 ∂X3 ∂X1 ∂u1 + ∂u2 ∂X2 ∂X1
⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦
2.1 位移与应变张量（15）
⎡∂
若令矩阵微分算符▽s为如下形式：
dX3
+
∂u 3 ∂X1
dX1
+
∂u 3 ∂X 2
dX 2
+
∂u 3 ∂X3
dX3
⎪ ⎪ ⎭
Δ
=
(d
→
L′)2
− (d
→
L)2
=
dX1′2
+
dX
′2
2
+
dX