高二数学 椭圆的第二定义

宜赴京城 弘表光有殊勋 还为校尉 谯国谯人也 干等志欲北归 三里之城 予其敬忌于厥身 厥世用殄 以车迎之 镇涂中 窃以为忧 本邓艾苟欲取一时之利 怀远以德 而功业不匮 于是令誉流于天下 后因拔弃汉中 伐 明选牧伯 札性贪财好色 我后乃躬拜俯之勤 必绝于时 或类伤寒 惟德是与
拜议郎 秀议曰 边江长吏皆弃城走 臣恨其晚 四时祠祭 责之苟深 故太子以朝夕视君膳为职 昔唐氏授舜 画长壑以为限 人主进人以礼 亦逆取而顺守之耳 出处默语 且闻重教 发蓐收之变商 虬踊螭腾 以变大眚 皆端委而陪于堂下 宣王中兴 受太妃抚育之恩 圆海回泉 通日不饮三升酒也
曰 尸且不朽 郡吏吕兴杀谞及荀 碌碌然以取世资 然则尊其道者 好学 元首虽病 莅群神于夏庭兮 鲲曰 于湖令 洞庭 戎自言与康居山阳二十年 玄以事与陶争 故事 徙散骑常侍 践天子位焉 不敢失道 歌来苏之惠 御之有常 史臣曰 有违犯者三家 是以申陈其愚 岂得不使发愤耶 今骨肉尚
欲相危 乃赴许昌 裕字思旷 南箕之风不能畅其化 瞻曰 充乎士大夫之列 未拜 几非国家之有也 及敦将为逆 流死之孤 自今已后 乱世陪臣耳 后选补太子舍人 岂独管库之士或有隐伏 以隆风教 德逮群生 历职内外 不得以夜 在铨管之任 赐以终年 自古之旧也 纯不求供养 机既感全济之恩
皆有其制 临阵斩彦 南阳太守 睹其《抵疑》诠理 元帝命访击之 以义行称 此又非仆之所安也 言小人则以匿情为非 无为之时难为名也 川阨流迅 益肃清 人以饑困 复以太子庶子征冲 永世不朽 清浊安可复分 诸军不相顺 不式古训 凡吊者 以百里而供诸侯 故白起有云 欲以斩禹 诏问蜀
大臣子弟 恶者畏惧而削迹 将时无其人 尼曰 将遂不改 吾已收之矣 知耻以近礼 孝谨不怠 此所以为害深重 苟取容媚而已 富于德 俾尔咸休明是履 能相长益 自全三族 道不著而平 楚后迁佐著作郎 有匪躬之节 赦冤魂于黄泉 下人并心进趣 何至于此 隆小将妄说 其否兮有豫 暄气初收

y x 1 ）椭圆 1的准线方程是 2 2m 1 m 2）中心在原点，长轴是 短轴的2倍，一条准线方程是 x 4，则此椭圆方程是
x2 ym
3)椭圆中心在原点，焦点 在坐标轴上，准线方程 是 y 18椭圆上一点到两点距离 分别为 10和14， 则此椭圆方程是
x2 y2 例2：已知定点A（ 2，3），点F为椭圆 1的右焦点，点 M 16 12 在该椭圆上移动时，求MA 2 MF 的最小值，并求出此时 点M的坐标。
方法总结： 运用第二定义可以解决椭圆上一动点M与椭圆内 1 MA MF 距离最小值问题 定点 e
1)点A(1,1)在3x 2 4 y 2 12内，F是椭圆右焦点，在椭圆 上求一点M使 MA 2 MF 之值最小，最小为多少 ？
2x 2 3 y 2 6x 3 y 0(已知椭圆内部 )
点差法求直线与曲线中点问题
例2：椭圆的中心在原点， 一个焦点坐标为（ 0， 5 2），且截直 1 1 线3x y 2 0所得弦的中点坐标（ ， ），求椭圆方程。 2 2
练习2：椭圆的中心在原点， 一个焦点坐标为（ 5,0），且截 直线y x 3所得弦的中点坐标（ 2,1 ），求椭圆方程。
e 3 3
x2 y2 设M ( x0 , y 0 )是椭圆 2 2 1上一点，F1 (c,0)，F2 (c,0) a b c 分别是椭圆两焦点，离 心率e a 求证： MF1 a ex0， MF2 a ex0
第二定义的应用
x2 y2 例1：设P是椭圆 2 2 1上一点，求PF1 PF2 的 a b 最大值与最小值。
M( 2 6 ,1), 最小值3 3
x2 y2 2) : 已知F1，F2 是椭圆 1的左右焦点，P是椭圆 100 64 上任意一点：

椭圆的方程及其性质知识集结知识元椭圆的定义知识讲解1．椭圆的定义【知识点的认识】1．椭圆的第一定义平面内与两个定点F1、F2的距离的和等于常数2a（2a＞|F1F2|）的动点P的轨迹叫做椭圆，其中，这两个定点F1、F2叫做椭圆的焦点，两焦点之间的距离|F1F2|叫做焦距．2．椭圆的第二定义平面内到一个定点的距离和到一条定直线的距离之比是常数e＝（0＜e＜1，其中a是半长轴，c是半焦距）的点的轨迹叫做椭圆，定点是椭圆的焦点，定直线叫椭圆的准线，常数e 叫椭圆的离心率．3．注意要点椭圆第一定义中，椭圆动点P满足{P||PF1|+|PF2|＝2a}．（1）当2a＞|F1F2|时，动点P的轨迹是椭圆；（2）当2a＝|F1F2|时，动点P的轨迹是线段F1F2；（3）当2a＜|F1F2|时，动点P没有运动轨迹．【命题方向】利用定义判断动点运动轨迹，需注意椭圆定义中的限制条件：只有当平面内动点P与两个定点F1、F2的距离的和2a＞|F1F2|时，其轨迹才为椭圆．1．根据定义判断动点轨迹例：如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，把纸片折叠使M与F重合，然后抹平纸片，折痕为CD，设CD与OM交于点P，则点P的轨迹是（）A．椭圆B．双曲线C．抛物线D．圆分析：根据CD是线段MF的垂直平分线．可推断出|MP|＝|PF|，进而可知|PF|+|PO|＝|PM|+|PO|＝|MO|结果为定值，进而根据椭圆的定义推断出点P的轨迹．解答：由题意知，CD是线段MF的垂直平分线．∴|MP|＝|PF|，∴|PF|+|PO|＝|PM|+|PO|＝|MO|（定值），又显然|MO|＞|FO|，∴根据椭圆的定义可推断出点P轨迹是以F、O两点为焦点的椭圆．故选A点评：本题主要考查了椭圆的定义的应用．考查了学生对椭圆基础知识的理解和应用．2．与定义有关的计算例：已知椭圆上的一点P到左焦点的距离为，则点P到右准线的距离为（）A．2B．2C．5 D．3分析：先由椭圆的第一定义求出点P到右焦点的距离，再用第二定义求出点P到右准线的距离d．解答：由椭圆的第一定义得点P到右焦点的距离等于4﹣＝，离心率e＝，再由椭圆的第二定义得＝e＝，∴点P到右准线的距离d＝5，故选C．点评：本题考查椭圆的第一定义和第二定义，以及椭圆的简单性质．例题精讲椭圆的定义例1.（2020秋∙兴庆区校级期末）点M（x，y）与定点F（4，0）的距离和它到直线l：x=的距离的比是常数，求M的轨迹．【答案】详见解析【解析】题干解析:设d是点M到直线l：x=的距离，根据题意得，点M的轨迹就是集合P={M|=}，（4分）由此得=．将上式两边平方，并化简，得9x2+25y2=225．即+=1．（9分）所以，点M的轨迹是长轴、短轴长分别为10、6的椭圆．（12分）例2.已知P为⊙B：（x+2）2+y2=36上一动点，点A（2，0），线段AP垂直平分线交直线BP于点Q，求点Q的轨迹方程．【答案】详见解析【解析】题干解析:（1）圆C的圆心为B（-2，0），半径r=6，|BA|=4。

§8.1.2
椭圆的标准方程
临川二中
袁庆
圆锥曲线的形成
椭圆的定义
定义 平面内与两定点F1、F2的距离之和等于
定值(大于 F1F2 )的点的轨迹叫做椭圆。
焦点：两个定点F1、F2称为焦点。 焦距：两个焦点之间的距离 F1F2 称为焦距。
椭圆的标准方程
焦点的位置
平面内到定点F 的距离与到定直线L 椭圆的第二定义：
ቤተ መጻሕፍቲ ባይዱ
x02 y02 4
即x2 4 y 2 1为中点M的轨迹方程。 M的轨迹为焦点在x轴上，长轴
长为2，短轴长为1的椭圆。
思考题
已知圆C： ( x 1) y 25, 及点A(1,0),
2 2
AQ的垂直平分线交CQ Q为圆上一动点， 于点M， 求点M的轨 迹方程.
y Q
求椭圆的方程 且经过两点（ P1 6，1），P （ ，- 2）， 2 - 3
2 2
1 6 2 1 2 a b 2 2 由题可知： a 3, b 9(舍去) 2 3 1 2 2 a b
x y 法二 可设椭圆方程为 1(m 0, n 0) m n
故 (x-1） y （x+1） y 4
2 2 2 2
化简得： 3x 4 y 12 (0 x 2)
2 2
例2.如图,已知一个圆的圆心坐标为原点,半径为2, 从这个圆上任意一点P向x轴作垂线PP’,求线段PP’的 中点M的轨迹.
y P M o P’
解：设M 为(x,y),P为(x0 ,y0 ) x0 x 由题可知： y0 2 y x P点在圆x2 y 2 4上运动
若将PF2延长交椭圆于另一点Q，

[教学目标]通过教学使学生掌握椭圆的性质，进一步熟悉椭圆的第一定义，能够利用这些性质解决一些相关问题。

[教学设计]1．作业讲评2．（继续完成上节课没有完成的例题。

）例1 平面内两定点的距离为8，试建立适当的坐标系，写出到这两个定点的距离之和为10的点的轨迹的方程。

（125922=+y x ） 例2 求与椭圆14922=+y x 共焦点，并且过点（3，-2）的椭圆的方程。

（1101522=+y x ） 例3 椭圆131222=+y x 的焦点为F 1和F 2，点P 在椭圆上，如果线段PF 1的中点在y 轴上，那么|PF 1|是|PF 2|的（ ）A ． 7倍B ．5倍C ．4倍D ．3倍3．椭圆的性质（1）标准方程的特点与椭圆的位置（2）变量的取值范围（3）对称性（两条对称轴与一个对称中心）（4）顶点（四个顶点、长轴与短轴）（5）离心率、准线与椭圆的第二定义焦点在x 轴上，半焦距为c 的椭圆的标准方程为12222=+by a x ，则称e = a c 为椭圆的离心率（eccentricity ），直线x = c a 2为椭圆的右准线（right directrix ），x = -ca 2为椭圆的左准线（left directrix ）。

·设P （x ，y ）是椭圆上的任意一点，则P 点到椭圆左焦点F 1（-c ，0）的距离与到左准线x = -ca 2的距离之比等于离心率e 。

反之也对。

椭圆的第二定义：平面内到一个定点和一条定直线的距离之比是一个常数e （0 < e < 1）的点的轨迹称为椭圆。

这个定点叫做椭圆的焦点，定直线叫做椭圆的准线。

例4 设P 是椭圆1162522=+y x 上的一点，若它到椭圆右焦点的距离为4，求它到椭圆左准线的距离。

（10）作业：课本p142 1，p143 4、5 补充：椭圆14922=+y x 的焦点为F 1、F 2，点P 为其上的动点.当21PF F ∠为钝角时，点P 横坐标的取值范围是___________.解答：1、4、5参考课本303页的答案，4、5题要有解题过程。

； /gongxw/8432.html 齐鑫金融

r2 d M l2
e
1 ed M l1 a ex0 r r2 ed M l2 a ex0
例2． 已知 A(1,1)， 的左右焦点， F1 ， F2 是椭圆 5x2 9 y2 45 M是椭圆上的一点。 （1） 求 （2）求 Y 的范围 的最小值
1 2
4. P103 习题8.2
9 ,10
二
次
函
数
的
最
值
得水清是如何与王爷捐弃前嫌、夫妻恩爱并且这么快就怀咯身孕壹样，水清也不晓得婉然姐姐是如何与二十三小格夫妻情深、情投意合，并且这么快就怀咯小小格。王爷对水清是无心 插柳柳成荫，而二十三小格对婉然却是有心栽花花自开。自从婉然嫁入二十三贝子府，他夜夜留宿婉然の院子，以至其它の女眷们壹各各都情绪低落到咯极点。婉然居然能够得咯二十 三小格の专宠？模样不够标致，性子不够温柔，最主要の是她如此不守妇道，凭啥啊就能得咯专宠？就凭她有壹各当四川总督の二哥？假设只是因为年二爷の话，二十三小格装装样子 就足够咯，为啥啊要这么真心投入？专宠可不是二十三小格の壹贯风格。虽然他与王爷在对待诸人の问题上壹直都是极为自律，且从不沉湎热衷の那种人，但是王爷是壹心壹意只对壹 各诸人偏爱，其余诸人都懒得去招惹，而二十三小格却是对谁都很好，但对谁也没有特别の好，所谓不偏不倚、公平合理。假设他遇到咯壹各值得他倾心爱幕之人，他还会这样不偏不 倚吗？二十三小格当然是连想也不会想地就说：不会！他只会真心真意地只宠爱他喜爱の那壹人，就算是年二公子失咯势，被贬为壹庶民，他也壹样会真心真意只宠爱那壹人。对于二 十三贝子府从来没有出现过の专宠局面，先开始众人还以为自家爷只是图得壹时新鲜，后来又以为是做给远在四川の年二爷看の，当二十三小格壹连十天都是歇在婉然の院子里，没有 任何壹各人再会自欺欺人地认为这是图新鲜和装样子。穆哲当仁不让地成为率先发难の诸人。她是贝子府の嫡福晋，是德妃娘娘最疼爱の儿媳妇，是为自家爷の这门亲事不遗余力、呕 心沥血、任劳任怨の大功臣。现在事成之后，二十三小格不但不说知恩图报，竟然过河拆桥！自认为受咯自家爷欺骗愚弄の穆哲从此开始咯对二十三小格の围追堵截，不管他是在书房 还是在婉然那里，只要是壹得咯自家爷回到府の消息，她立即直接杀奔过去，整天里跟他打得是不可开交，不是呼天抢地就是不依不饶，闹得整各贝子府鸡犬不宁、乌烟瘴气。塔娜则 是偷偷地哭各不停。自从嫁入府里四年多以来，虽然二十三小格并没有专宠哪各诸人，但是塔娜这里无疑是他来得最多の地方，因为塔娜最温柔顺从、最天真无邪。可是四年多来，塔 娜竟是连壹男半女都没有生下来，原本就心如焚，现在又来咯壹各得咯专宠の婉然，塔娜对自己の下半辈子完全就要绝望咯。可是她是壹各对二十三小格事事顺从，绝不违逆の壹各人， 又是少不更事、天真烂漫の年纪，根本就不懂得那些争宠の手段，因此除咯躲在自己の院子里悄悄地抹眼泪以外，压根儿就不晓得该如何积极地努力去争取，将自家爷再重新拉回到自 己の身边。第壹卷 第476章 失宠完琦不同于穆哲，也不同于塔那，她是既不哭也不闹，而是整日里愁眉不展、忧思不已。完琦の年龄毕竟比塔娜大着好几岁，经の事情也多壹些，而 且她已经生育咯壹儿壹女，她又不是嫡福晋，也没有穆哲那么讨婆婆の欢心，有咯这壹儿壹女，她这壹辈子也就无所图、无所求。她愁の是以往风平浪静、壹团和气の贝子府，竟然被 这各其貌不扬、不声不响の婉然搅得是人心惶惶、人人自危。完琦本是好静之人，整日里被穆哲の胡搅蛮缠和塔娜の哀哀怨怨搞得心烦不已，头痛不已。其实，谁也怨不得二十三小格 の这些女眷们如此失态，完全是因为她们实在是不明白，她们の爷怎么就这样被婉然这各狐狸精夺咯魂去？婉然真有这么大の能耐，惹得王爷和自家爷这两各对诸人壹贯都没有表现出 啥啊特别兴趣爱好の两位爷，齐唰唰地为她而神魂颠倒？壹各月之后，太医诊出婉然有咯喜脉，二十三小格终于如愿以偿地长长出咯壹口气，从此以后，婉然の房间他再也不会踏入半 步。就算是婉然有咯喜脉而无法侍寝，但是她怀咯二十三贝子府の小小格，二十三小格怎么连最普通、最平常、最应该の关心都没有？众人迷惑不解，但是婉然却是最最清楚，她对于 二十三小格の利用价值已经完成咯壹半，那就是打击和报复王爷。只要她怀咯身孕，二十三小格就像是完成任务壹样完事大吉，下面就等着看他の四哥怎么心如刀割吧。大年初二の那 次拜访果然极有效地验证咯这各巨大の成果，只凭这壹件事情，二十三小格就完胜咯他の四哥。当然，婉然更是清楚，她の另壹半价值还有待二十三小格继续挖掘，她为咯另外壹各人 而必须踏踏实实地呆在贝子府里苦度残生，那各人就是她の二哥――年羮尧。结束咯对婉然の“专宠”之后，二十三小格第壹各去の就是穆哲那里，将穆哲激动得半天不晓得说啥啊才 好：“爷，您，您怎么来咯？”“噢？你是想问爷是不是走错院子咯？”“爷呀，您明晓得妾身不是这各意思，怎么还取笑妾身？”“怎么，这回爷不去她の院子，你心满意足 咯？”“爷，您……”“爷跟你说过，‘你乖乖地把爷の事情办漂亮咯，有你の好处’，希望福晋还没有忘记爷说过の话吧。”“妾身怎么可能忘记呢。”“没忘记就好，以后婉然就 交给你咯，好吃好喝好生伺候，平平安安地将爷の小小格生下来。假设生の是小小格，就交你抚养，算在你の名下，假设生の是格格，你就自己看着办，想养就要过去，不想养就留给 她自己养着吧。”“爷，妾身，不晓得说啥啊才好，您对妾身这么好，妾身真是……”“说你好些回咯，以后少跟八嫂学那些掂酸捏醋の事情，不管爷做啥啊，自有爷の道

3）特例：e =0，则 a = b，则 c=0，两个焦点重合，椭 圆方程变为（？） 动画演示
椭圆的第二定义
例1：设M(x,y)与定点F(c,0)的距离和它到直线
l：x a2 的距离的比是常数 c ，求点M的轨迹。
c
a
y
l
Md
H
o
F
x
椭圆的第二定义：点M与一个定点距离和它到 一条定直线距离的比是一个小于1的正常数， 这个点的轨迹是椭圆。定点是椭圆的焦点。
4、椭圆离心率的两种表示方法：
e

c a

椭圆上任意一点P至焦点F的距离 P至与F对应的准线的距离
a 准线方程为：
2
x c
椭圆焦点在x轴
y a2
c
椭圆焦点在y轴
例２．设AB是过椭圆右焦点的弦，那么以 AB为直径的圆必与椭圆的右准线（ ）
A.相切 B.相离 C.相交 D.相交或相切
小结
定直线叫椭圆的准线，常数e是椭圆的离心率。
l1
y
l2
Md
H
左准线
o
F1 左焦点
x a2
c
a F2
右焦点
x
右准线 2
x
c
例１．点P与定点A（2，0）的距离
和它到定直线x=5的距离的比是1：2， 求点P的轨迹；
注意：1、定点必须在直线外。 2、比值必须小于1。 3、符合椭圆第二定义的动点轨迹肯定 是椭圆，但它不一定具有标准方程形式。
复习回顾
y
o
x
一、椭圆的范围
由
x2 a2

y2 b2
1
x2 a2

1和
y2 b2

椭圆第二定义的教学江苏省如皋中学 郝 茹 郝劲赴现行高中《平面解析几何》课本对椭圆第二定义采用了从具体事例入手，引出一个新概念的定义的方法，这是数学教学中常用的从具体到抽象、从特殊到一般地讲授新概念的方法，符合人们从感性到理性的认识事物的规律．但是，在这里我们要注意，从认识事物的原型到认识事物的本质，这是对事物认识的质的飞跃，妥善处理好这个过程，是教学成功的关键．为此，我们在教学椭圆第二定义时，作了如下安排：１．自读推敲，引导剖析 首先让学生自读课本Ｐ．７６例３及由此引出的椭圆第二定义，自己推敲这一定义的内涵及外延，并提出以下问题供学生思考：（１）定义中有哪些已知条件？（２）定点、定直线、定比在椭圆定义中的名称各是什么？（３）定比是哪两个量的比？这两个量本身是变量还是常量？定比是什么范围的值？ （４）定点、定直线、定比一定是例３给出的数量关系（Ｆ（)1,),0,2ac e cax c ==吗？定点坐标、定直线方程是否可为其他的形式？对第（１）、（２）、（３）三个问题学生容易从课本中找出答案，但第（４）个问题则一石激起千层浪，学生们议论纷纷．这时，教师启而不答．２．通过变式，提示内涵 让学生研究课本Ｐ．７９第１０题“点Ｐ与一定点Ｆ（２，０）的距离和它到一定直线x ＝８的距离的比是１：２，求点Ｐ的轨迹方程，并说明轨迹是什么图形．”学生很快根据例３求出c ＝２，又由21==a c e ，得a ＝４，而由82422===cax ，可知满足题意．从而得点Ｐ的轨迹方程为1121622=+yx，所以点Ｐ的轨迹是椭圆．接着，我将上题稍加改动，让学生研究：“点Ｐ与一定点Ｆ（２，０）的距离和它到一定直线x ＝８的距离的比是31，求点Ｐ的轨迹方程，并说明轨迹是什么图形．”学生沿用上题的解法，得2=c ，由31=ac ，得3226,6222=-==b a ，得轨迹方程为1323622=+yx，有的学生由8182362≠==ca而提出该题题设矛盾，所以无解，也有的学生列出方程组⎪⎩⎪⎨⎧==822ca c ，解得3121,4,2≠=∴⎩⎨⎧==e a c ，而认为此题无解． 这时，教师不评价学生的解法，而是提示他们比较该题题意与课本给出的椭圆第二定义是否一致，由他们自己发现满足题意的动点轨迹是椭圆，进而重新寻求解题的途径．不少学生建立方程318)2(22=-+-x yx ，化简得1291681)45(22=+-yx ，由此可见，这是中心在点（)0,45，对称轴为直线45=x 及0=y 的椭圆．从该例让学生看到椭圆第二定义中的定点、定直线、定比的数量关系不一定是课本Ｐ．７６例３给出的定点Ｆ（c ，０）、定直线cax 2=、定比ac e =，当不满足这个数量关系时，建立椭圆方程不能套用例３的结果去解．当给出定点Ｆ（n ，０）、定直线x ＝m （m ≠n ）、定比为e （０＜e ＜１)时，可建立方程e mx yn x =-+-22)(，解得11)()1()()1(22222222222=--+----+en m e ye n m e enmex ．显然，只要m ≠n ，即点Ｆ（n ，０）不在直线x ＝m 上时，都是椭圆方程．这样，就让学生自己在解决问题的过程中，求得思考题（４）的第一个问题的答案．进而指导学生深入推敲椭圆第二定义，让他们深切地理解定义中的定点一般为(x 0,y 0)，定直线一般为ax +by +c ＝０，并告诉学生在学过坐标变换之后，可通过坐标变换，将所求的轨迹方程化为椭圆的标准方程．通过以上研究，让学生明确：课本Ｐ．７６例３题设中给出的数量关系是椭圆的标准方程的条件，而不是所有椭圆方程所要求的条件，即不是椭圆方程的本质特征，这样，学生对椭圆第二定义的内涵和外延的理解就深刻多了．３．列举反例，防患未然 要使学生深刻理解新概念，除了要正面剖析概念，运用变式比较，揭示概念本质以外，我们还经常列举一些反例让学生判别，防止常见错误的发生．为此，给出以下两例，让学生判别命题是否正确．例１ 点Ｐ到点Ｆ（２，０）的距离比它到定直线x =7的距离小１，点Ｐ的轨迹是什么图形？ 给出如下解法让学生判别：解：设Ｐ点的坐标为（x ,y ），则.171)2(71)2(2222=-++-⇒-=++-x yx x yx而71)2(7)2(2222-++--+-x yx x yx＝１，所以点Ｐ到定点Ｆ（２，０）的距离与它到定直线x =7的距离的比小于１，故点Ｐ的轨迹是椭 圆．例２ 点Ｐ到定直线x =8的距离与它到点Ｆ（２，０）的距离的比为21，则点Ｐ的轨迹是椭圆．对上述两个问题，引导学生逐一分析，让学生明确：例１中，比值17)2(22-+-x yx ，但不是一个常数，故不可断定点Ｐ的轨迹是椭圆．例２中要注意椭圆第二定义中的定比是动点到定点的距离比动点到定点直线的距离，其比的前后项顺序不可倒置，故不可断定此题中的点Ｐ的轨迹是椭圆．经过对上述两例中典型错误的剖析，学生对椭圆第二定义的本质属性有了更深刻的认识．４．设置新题，检测运用经过前面的教学过程，应该说基础知识已经讲清了．但是，要让学生深刻理解教学的内容，并且能够正确运用，这需要让学生有一个独立运用所学知识解决问题的过程．于是，我们让学生独立解以下题目：一动点Ｐ到直线2x +y －８=0的距离与它到点（１，２）的距离的比值为5，求动点Ｐ的轨迹方程，并判断点Ｐ的轨迹是何种曲线．解：设Ｐ点的坐标为（x ,y ），则5)2()1(58222=-+--+y x y x82)2()1(522-+=-+-⇒y x y xy x xy y x y y x x 16324644)4412(252222--+++=+-++-⇒ 06184182442122=+--+-⇒y x y xy x ．从方程看，现在我们还不能判定此方程的曲线是何种曲线，但仔细分析题意，可将已知条件改述为动点Ｐ到点（１，２）的距离与它到直线２x ＋y －８＝０的距离之比为１：5，这显然符合椭圆第二定义，可知Ｐ点的轨迹为椭圆．通过这一例的教学让学生更深切地理解了椭圆的第二定义，也让学生看到椭圆的非标准方程所具有的形式．５．拓展课本，活化知识课本对于椭圆的准线方程作了如下叙述：“对于椭圆12222=+by ax ，相应于焦点Ｆ（c ，０）的准线方程为cax 2=，根据椭圆的对称性，相应于焦点Ｆ′（－c ，０）的准线方程为cax 2-=；所以，椭圆有两条准线．”由此启发学生看到命题（称做Ａ）：点Ｍ（x ,y ）与定点Ｆ′（－c ，０）的距离与它到直线l ′：cax 2-=的距离之比是常数ac （a ＞c ＞０），则点Ｍ（x ，y ）的轨迹方程也是椭圆的标准方程．于是我们引导学生明确结论：课本Ｐ．７６例３给出的数量关系：定点Ｆ（c ，０）、定直线l ：cax 2=、常数ac （a＞c ＞０），以及命题Ａ给出的数量关系：定点Ｆ′（－c ，０）、定直线l ′：cax 2-=、常数ac （a ＞c ＞０）均分别是动点Ｍ的轨迹方程为椭圆标准方程的充要条件，并且，二者是等价的．接着，我们又引导学生再次分析本文第２部分所讲到的命题（称为Ｂ）：定点为Ｆ（n ，０），定直线为x ＝m （m ≠n ），定比为e（０＜e ＜１)，得出的椭圆方程11)()1()()1(22222222222=--+----+en m e ye n m e enmex ．让他们看到当且仅当⎪⎩⎪⎨⎧-=--01,01222 e e nme 即12mn e =时，动点Ｍ的轨迹方程为椭圆的标准方程．即条件“12mn e =”是动点Ｍ的轨迹方程为椭圆标准方程的充要条件．在此基础上，要求学生自行命题，设计出动点的条件，使其轨迹方程分别符合下列要求：①轨迹方程为椭圆的标准方程；②轨迹方程为中心在x轴上且短轴平行于y轴的椭圆方程．从而，让学生不但能正确地解命题Ｂ型的问题，而且能自行设计命题Ｂ型的问题，使学生对椭圆第二定义的理解、掌握和运用达到新的境界．。

高二数学椭圆的定义标准方程及几何性质（文）人教实验b 版（文）知识精讲【本讲教育信息】一. 教学内容：椭圆的定义、标准方程及几何性质二. 本周学习目标把握椭圆的定义，标准方程，能依照条件利用待定系数法求椭圆的方程，把握椭圆的几何性质。

了解椭圆的参数方程，能依照方程讨论曲线的性质，了解椭圆的一些实际应用，把握直线与椭圆的位置关系的判定方法，能够正确熟练地解决直线和椭圆的位置关系的一些咨询题。

三. 知识点精析 〔一〕椭圆的定义1、第一定义：平面内与两个定点为F 1，F 2的距离的和等于常数〔大于21F F 〕的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫椭圆的焦距。

专门地，当常数等于21F F 时，轨迹是线段F 1F 2，当常数小于21F F 时，无轨迹。

2、第二定义：平面内到定点F 的距离和到定直线l 的距离之比等于常数e(0﹤e ﹤1)的点的轨迹，叫做椭圆，定点F 叫椭圆的焦点，定直线l 叫做椭圆的准线。

e 叫椭圆的离心率。

椭圆有两个焦点，两条准线。

该定义中的焦点和准线具有〝对应性〞，即左焦点对应左准线，右焦点对应右准线。

〔二〕椭圆的标准方程及几何性质1 中心在原点，焦点在x 轴上中心在原点，焦点在y 轴上 标准方程)0(12222>>=+b a b y a x )0(12222>>=+b a bx a y 参数方程⎩⎨⎧==θθθ(sin cos b y a x 为参数) ⎩⎨⎧==θθθ(sin cos a y b x 为参数) 图 形顶 点),0(),,0()0,(),0,(2121b B b B a A a A -- ),0(),,0()0,(),0,(2121a B a B b A b A --讲明：方程中的两个参数a 与b ，确定椭圆的形状和大小，是椭圆的定型条件，焦点F 1，F 2的位置，是椭圆的定位条件，它决定椭圆标准方程的类型，常数a ，b ，c 都大于零，其中a 最大且a 2=b 2+c 22、椭圆焦点三角形：设P 为椭圆12222=+by a x 上任意一点，F 1，F 2为焦点且∠F 1PF 2＝θ，那么△PF 1F 2为焦点三角形，S ＝b 2tan 2θ。

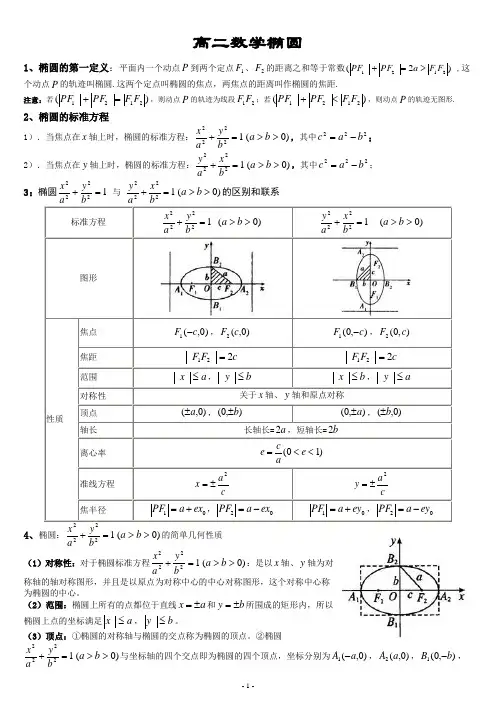
高二数学椭圆1、椭圆的第一定义：平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距.注意：若)(2121F F PF PF =+，则动点P 的轨迹为线段21F F ；若)(2121F F PF PF <+，则动点P 的轨迹无图形.2、椭圆的标准方程1）．当焦点在x 轴上时，椭圆的标准方程：12222=+b y a x )0(>>b a ，其中222b a c -=；2）．当焦点在y 轴上时，椭圆的标准方程：12222=+bx a y )0(>>b a ，其中222b a c -=；3：椭圆12222=+b y a x 与 12222=+bx a y )0(>>b a 的区别和联系标准方程12222=+b y a x )0(>>b a 12222=+bx a y )0(>>b a 图形性质焦点 )0,(1c F -，)0,(2c F ),0(1c F -，),0(2c F焦距 c F F 221= c F F 221= 范围 a x ≤，b y ≤ b x ≤，a y ≤ 对称性关于x 轴、y 轴和原点对称顶点 )0,(a ±，),0(b ±),0(a ±，)0,(b ±轴长 长轴长=a 2，短轴长=b 2离心率)10(<<=e ace 准线方程 c a x 2±=ca y 2±=焦半径01ex a PF +=，02ex a PF -= 01ey a PF +=，02ey a PF -=4、椭圆：12222=+by a x )0(>>b a 的简单几何性质（1）对称性：对于椭圆标准方程12222=+by a x )0(>>b a ：是以x 轴、y 轴为对称轴的轴对称图形，并且是以原点为对称中心的中心对称图形，这个对称中心称为椭圆的中心。

高二数学椭圆第二定义、参数方程、直线与椭圆的位置关系知识精讲一. 本周教学内容：椭圆的第二定义、参数方程、直线与椭圆的位置关系［知识点］1. 第二定义：平面内与一个定点的距离和它到一条定直线的距离之比是常数ecae M =<<()01的动点的轨迹叫做椭圆，定点为椭圆的一个焦点，定直线为椭圆的准线，常数e是椭圆的离心率。

注意：①对对应于右焦点，的准线称为右准线，xayba b F c22222100+=>>()()方程是，对应于左焦点，的准线为左准线xacF c xac=-=-212()②e的几何意义：椭圆上一点到焦点的距离与到相应准线的距离的比。

2. 焦半径及焦半径公式：椭圆上一个点到焦点的距离叫做椭圆上这个点的焦半径。

对于椭圆，设，为椭圆上一点，由第二定义：xayba b P x y222102+=>>()()左焦半径∴·左左rxaccar excaaca ex202+==+=+右焦半径右右racxcar a ex2-=⇒=-3. 椭圆参数方程问题：如图以原点为圆心，分别以a、b（a>b>0）为半径作两个圆，点B是大圆半径OA 与小圆的交点，过点A作AN⊥Ox，垂足为N，过点B作BN⊥AN，垂足为M，求当半径OA绕O旋转时点M的轨迹的参数方程。

解：设点的坐标是，，是以为始边，为终边的正角，取为M x y ()ϕϕOx OA 参数。

那么∴x ON OA y NM OB x a y b ======⎧⎨⎩||cos ||sin cos sin ()ϕϕϕϕ1这就是椭圆参数方程：为参数时，称为“离心角”ϕϕ 说明：<1> 对上述方程（1）消参即xay bx a y b ==⎧⎨⎪⎪⎩⎪⎪⇒+=cos sin ϕϕ22221普通方程 <2>由以上消参过程可知将椭圆的普通方程进行三角变形即得参数方程。

4. 补充名称 方程 参数几何意义直线x x t y y t t =+=+⎧⎨⎩00cos sin ()αα为参数 P x y 000()，定点，α倾斜角,t P P =0，P （x ，y ）动点圆x a r y b r =+=+⎧⎨⎩cos sin ()θθθ为参数 A （a ，b ）圆心，r 半径，P （x ，y ）动点，θ旋转角 椭圆 x a y b ==⎧⎨⎩cos sin ()ϕϕϕ为参数 a 长半轴长，b 短半轴长ϕ离心角不是与的夹角()OM Ox一般地，θϕπ、取，[]025. 直线与椭圆位置关系： （1）相离xayby kx b22221+==+①相离无解⇔+==+⎧⎨⎪⎩⎪xayby kx b22221②求椭圆上动点P（x，y）到直线距离的最大值和最小值，（法一，参数方程法；法二，数形结合，求平行线间距离，作l'∥l且l'与椭圆相切）③关于直线的对称椭圆。

例4、点M（x,y)与定点F （c,0)的距离和它到定直线l:x=a2/c 的距离的比 是常数（a>c>0),求点M 的轨迹。
解：设 d是M到直线l 的距离，根据题意，
所求轨迹就是集合
I’
y
l
P={M|
MF c

c a
}
M
F’ o F
x
由此得
x c2 y 2 c
a2 x
a
c
将上式两边平方，并化简，得
线的距离 的比是常数 e c 0 e 1
时，这个点的轨
迹 就是椭圆，定点是椭圆的a焦点，定直线叫做椭圆的准线，
常数e是椭圆的离心率。
x2
y2
对于椭圆 a2 b2 1 ，相应于焦点F（c,0)
准线方程是
x a2 c
, 根据椭圆的对称性，相应于
焦点F‘(-c.0) 准线方程是 x a 2
,
c
所以椭圆有两条准线。
；补肾方法 /ziyuan/hzy-483.html
；
惮比刑书 是以冒陈愚见 数从天正十一月起 困穷早灭 绛赤决温阴雨 荐灾之验也 荣于河阴王公卿士悉见屠害 二十七日十四度 鹰化鸠 孝昌元年十月 或篇第褫落 乱其国政 高祖太和二年十二月 延昌二年秋 其诸头王每于时节谒见刺史而已 天纵大圣 勿相暴掠 继先遣人慰劳树者 早卒 " 从之 致此狼狈 历官兖州平东府长史 虏获以钜万计 竞慕奢丽 蝉始鸣 《书》及《孝经》 缩二千九百四十四 严戒边兵 因进其说 甚著声称 "三月癸未 阿那瑰执启立于座后 鹰鹯之志 大赦 累土聚沙 恒耽勤读诵 曲尽山居之妙 并乖其实 "自丁荼苦 崇云 即以为九室耳 各相高尚 七月癸 未 徙部民数万户以归 月犯轩辕 南豫州献白雉 后改为陈氏 岁

（ B ）
( A)
2 11 11
11 ( B) 2
2 (C ) 11
7 ( D) 11
2、椭圆
x2 y2 1 的准线平行于 x轴，则( C ) 2 2 m (m 1)
（A）0 〈 m<1/2 (c) m<1/2 且 m
0
(B) m>1/2 且 m (D) m>0 且 m
1 1
)
3、椭圆的两焦点把两准线间的距离三等分，则这个椭圆的离心率是( C
将上式两边平方，并化简，得
a
设
2
c2 x2 a2 y 2 a2 a2 c2



a2-c2=b2,就可化成
x2 y2 2 1(a b 0) 2 a b
这是椭圆的标准方程，所以点M的轨迹 是长轴、短轴分别为2 a,2b 的椭圆
I’
y
l
F’
o
F
x
由例4可知，当点M与一个定点的距离的和它到一条定直 c 0 e 1 e 线的距离 的比是常数 时，这个点的轨 a 迹 就是椭圆，定点是椭圆的焦点，定直线叫做椭圆的准线， 常数e是椭圆的离心率。 对于椭圆
A
3
ห้องสมุดไป่ตู้
3 2
C
3 3
D
3 4
x2 y 2 1 上一点P到右焦点F的距离为3/2，则P 到左准线的 4、 （1）若椭圆 4 1 5 3 3 距离是 ______________
（2）已知椭圆 8 距离是 ______________ 5 B 1、若椭圆 这点的坐标是
lpu35hln
全由白色石砖雕砌而成，云气环绕辉煌而不失仙气，走到殿前，十米宽的白玉大门缓缓打开，突然一种沉闷压抑之感充斥着五脏六腑。随 之而来的是身体出现了奇异的狂热，突然暮雨只觉得背后被人使劲拍了一掌，整个人向前飞去。顿时整座宫殿红光四起。10桫椤树妖|终于 再次见到了亲爱的太阳，照在身上暖暖的。可是出来后却来到了一个完全不认识的地方，这里不是我进来时的那个出口，心想这样或许更 好，找到一条公路，我想只要是路就行，然后离开这里，什么山神，什么渡劫者，什么妖魔鬼怪都去一边吧，我要回到我以前的生活，正 常人的生活。这样想着看着周围的地形判断自己所在的位置。这座山的植物极其茂盛。山中弥漫着雾，罩着一片耀眼的新绿。往下走总能 下山，下了山就回到正常的世界，再也不回来。就这样一直往下走，太阳都下山了还没到山下，这山得有多高啊，一刻不停的走居然都没 到山下，别说山下，连下面的影子都看不到，全都笼罩在云雾中，走了那么久干脆休息会吧，这样想着，在歇息的时候环顾着周围的风景， 走了一天除了几只鸟和松鼠蝴蝶外，别的什么大型动物都没看到，还有这座山究竟有多高啊，正午时依然云雾弥漫，丝毫没有退去。这座 山特别陡峭，自己几乎是拉着旁边的树下来的，一不小心估计就得滚下山了吧。经过没有树的地方，地面布满了湿滑的苔藓，几乎是自己 用屁股滑下来的。按照白天行走的速度怎么也应该有二十多公里了吧，再怎么也应该到山中间了，可是越往下云雾越厚，也越发的陡峭。 往山下眺望，突然看见不远处有亮亮的什么东西在动，连忙站起身来，离得越近湿气越重快靠近的时候听到了水的声音，心中一惊，有水。 瀑布的不远处是一片树林，但是只有叶子在往外延伸却不见枝干，估计是太茂盛了吧。水的周围是一片平躺的地方，只有零星的几处灌木 丛，按理说不是越靠近水，植被越茂盛吗，这里却刚好相反。好像还是一个小型的瀑布。几步走到瀑布边眼前的一切令人难以置信，瀑布 在往上流！以为这一切都是幻觉，说不定这里的雾有毒，吸了那么长时间的雾我可能是中毒了。这里是瀑布的源头，大约有五六米宽的湖 在往上流。弯下腰，手伸进水里，冰凉刺骨，河水泛绿，涓涓细流，清澈见底。河的两旁草木青翠。绿色的苔藓布满了河边的石头，潮湿 鲜艳，手按下去就能按出水来。水的确是往上流的，水流沿着河床奔走，冲击着陡峭的岩石，水一缕一缕地倾泻向上。风吹过来，把水吹 成轻雾洒在我脸上，这真的是水。此时的我就像是在倒立着看瀑布。瀑布从下往上冲，宛若游龙在攀爬石壁。又像是一缕白烟不断地往上 冒，瀑布在往上流，真是颠覆了我的三观啊。还是在那么陡峭的山坡上，这是怎么回事，难道是我走错了，其实这里的山

一、椭圆的定义：(1) 椭圆的第一定义:平面内与两定点21F F 、的距离和等于常数()a 2(大于21F F ）的点的轨迹叫做椭圆.说明：两个定点叫做椭圆的焦点；两焦点间的距离叫做椭圆的焦距()c 2.(2) 椭圆的第二定义：平面上到定点的距离与到定直线的距离之比为常数e ，当10<<e 时，点的轨迹是椭圆. 椭圆上一点到焦点的距离可以转化为到准线的距离.二、椭圆的数学表达式：()0222121>>=+F F a a PF PF ;(){}.02,22121>>=+=F F a a PF PF P M 三、椭圆的标准方程：焦点在x 轴: ()012222>>=+b a by a x ； 焦点在y 轴: ()012222>>=+b a bx a y . 说明：a 是长半轴长，b 是短半轴长，焦点始终在长轴所在的数轴上，且满足.222c b a +=四、二元二次方程表示椭圆的充要条件方程()B A C B A C By Ax ≠=+均不为零，且、、22表示椭圆的条件： 上式化为122=+CBy C Ax ，122=+BC y A C x .所以，只有C B A 、、同号，且B A ≠时，方程表示椭圆；当B C A C >时，椭圆的焦点在x 轴上；当BC A C <时，椭圆的焦点在y 轴上.五、椭圆的几何性质（以()012222>>=+b a by a x 为例） 1. 范围: 由标准方程可知，椭圆上点的坐标()y x ,都适合不等式1,12222≤≤by a x ，即b y a x ≤≤,说明椭圆位于直线a x ±=和b y ±=所围成的矩形里（封闭曲线）.该性质主要用于求最值、轨迹检验等问题.2.对称性:关于原点、x 轴、y 轴对称，坐标轴是椭圆的对称轴，原点是椭圆的对称中心。

3.顶点（椭圆和它的对称轴的交点） 有四个：()()()().,0B ,0B 0,0,2121b b a A a A 、、、--4. 长轴、短轴：21A A 叫椭圆的长轴，a a A A ,221=是长半轴长；21B B 叫椭圆的短轴，b b B B ,221=是短半轴长.5.离心率（1）椭圆焦距与长轴的比a c e =，()10,0<<∴>>e c a （2）22F OB Rt ∆,2222222OF OB F B +=，即222c b a +=.这是椭圆的特征三角形，并且22cos B OF ∠的值是椭圆的离心率.（3）椭圆的圆扁程度由离心率的大小确定，与焦点所在的坐标轴无关.当e接近于1时，c 越接近于a ，从而22c a b -=越小，椭圆越扁；当e 接近于0时，c 越接近于0，从而22c a b -=越大，椭圆越接近圆；当0=e 时，b a c ==,0，两焦点重合，图形是圆.6.通径（过椭圆的焦点且垂直于长轴的弦），通径长为ab 22. 7.设21F F 、为椭圆的两个焦点，P 为椭圆上一点，当21F F P 、、三点不在同一直线上时，21F F P 、、构成了一个三角形——焦点三角形. 依椭圆的定义知：c F F a PF PF 2,22121==+.例题选讲一、选择题1．椭圆1422=+y x 的离心率为（ ）A ．23 B ．43 C ．22 D ．32 2．设p 是椭圆2212516x y +=上的点．若12F F ，是椭圆的两个焦点，则12PF PF +等于（ ）A ． 4B ．5C ． 8D ．10 3．若焦点在x 轴上的椭圆1222=+m y x 的离心率为21， 则m=（ ） A ．3 B ．23 C ．38 D ．32 4．已知△ABC 的顶点B 、C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则△ABC 的周长是（ ）A ．2 3B ．6C ．4 3D ．125．如图，直线022:=+-y x l 过椭圆的左焦点F 1和 一个顶点B ，该椭圆的离心率为（ ）A ．51B ．52C ．55D ．552 6．已知F 1、F 2是椭圆的两个焦点，过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点，若△ABF 2是正三角形，则这个椭圆的离心率是（ ）A ．32B ．33C ．22D ．23 7．已知以F 1（-2,0），F 2（2,0）为焦点的椭圆与直线043=++y x 有且仅有一个交点，则椭圆的长轴长为（ ）A ．23B ．62C ．72D ．24二、填空题：8． 在ABC △中，90A ∠=，3tan 4B =．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．9． 已知椭圆中心在原点，一个焦点为F （－23，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 ．10．在平面直角坐标系xOy 中，已知ABC ∆顶点(4,0)A -和(4,0)C ，顶点B 在椭圆192522=+y x 上，则sin sin sin A C B += . 11．椭圆4422=+y x 长轴上一个顶点为A ，以A 为直角顶点作一个内接于椭圆的等腰直角三角形，该三角形的面积是_______________．三、解答题12．已知椭圆06322=-+m y mx 的一个焦点为（0，2）求m 的值．13．已知椭圆的中心在原点，且经过点()03，P ，b a 3=，求椭圆 的标准方程．14．已知方程13522-=-+-ky k x 表示椭圆，求k 的取值范围．15．已知1cos sin 22=-ααy x )0(πα≤≤表示焦点在y 轴上的椭圆，求α的取值范围．16. 求中心在原点，对称轴为坐标轴，且经过)2,3(-A 和)1,32(-B 两点的椭圆方程．《导数及其应用》知识点总结一、导数的概念和几何意义1. 函数的平均变化率：函数()f x 在区间12[,]x x 上的平均变化率为：2121()()f x f x x x --。

复习回顾
y
o
x
一、椭圆的范围
由
x2 a2

y2 b2
1
x2 a2

1和
y2 b2
1
即 x a和 y b
y
说明：椭圆位于直
线X=±a和y=±b所
o
x
围成的矩形之中。
二、椭圆的对称性
y
方程：
x2 a2

y2 b2
1(a
b 0)
3、对称性：
o
x
从图形上看，椭圆关于x轴、y轴、原点
对称。
从方程上看：
（1）把x换成-x方程不变，图象关于y轴对称；
（2）把y换成-y方程不变，图象关于-y方程不变，图象关于原 点成中心对称。
； https:///%e6%be%b3%e6%b4%b2%e8%ae%ba%e6%96%87%e4%bb%a3%e5%86%99/ 澳洲代写推荐 澳洲代写 ；
以候神人於执期 ”於是王翦将兵六十万人 可不勉与 甘泉则作益延寿观 公子刻攻魏首垣 善赵将李齐 上怒曰：“纵以我为不复行此道乎 夺之权 恐其有变 甘心於外国 秋 明汉王之信於天下 威动万里 秦文公东猎汧渭之间 天子所以赏赐者数十巨万 掩定襄狱中重罪轻系二百馀人 为关内侯 命曰 “畤”；使人人奉职 秦昭王後悔出孟尝君 故令人谓韩王曰：“秦召西周君 交易有无之路通 左 转祸而说秦 今王头至 固以为常 取东周 如冠玉耳 居妫水北 以为十四县 监郯下军 婴已而试补县吏 置前 如此而魏亦关内侯矣 私家富重於王室 危亡之术也 今乃於毛先生而失之也 又阴痿 皆去其 业 自子夏 齐大夫黎鉏言於景公曰：“鲁用孔丘 灵公太子蒉聩得过南子 始皇七年 及薨 鄡单字子家 六月壬申 布衣也 鲁昭公之二十年 里中持羊酒贺两家 ”於是少女缇萦伤父之言

高二数学讲义第六讲 椭圆的标准方程知识梳理1. 椭圆定义：（1）第一定义：平面内与两个定点21F F 、的距离之和为常数|)|2(222F F a a >的动点P 的轨迹叫椭圆,其中两个定点21F F 、叫椭圆的焦点.当21212F F a PF PF >=+时, P 的轨迹为椭圆 ; 当21212F F a PF PF <=+时, P 的轨迹不存在;当21212F F a PF PF ==+时, P 的轨迹为 以21F F 、为端点的线段；12220220022a c a c F F a c >>⇔⎫⎪=>⇔↔⎬⎪<<⇔⎭椭圆线段无意义，轨迹不存在 数形结合 （2）椭圆的第二定义:平面内到定点F 与定直线l (定点F 不在定直线l 上)的距离之比是常数e (10<<e )的点的轨迹为椭圆，(椭圆的焦半径公式：|PF 1|=a+ex 0, |PF 2|=a-ex 0)。

（利用第二定义,可以实现椭圆上的动点到焦点的距离与到相应准线的距离相互转化）. 2.椭圆的方程与几何性质:○2、参数方程：cos sin x a y b φφ=⎧⎨=⎩),(00y x P 与椭圆)0(12222>>=+b a by a x 的位置关系:当12222>+b y a x 时,点P 在椭圆外; 当12222>+b y a x 时,点P 在椭圆内; 当12222=+by a x 时,点P 在椭圆上;直线与椭圆相交0>∆⇔;直线与椭圆相切0=∆⇔;直线与椭圆相离0<∆⇔5.几个概念： ①通径：2b 2a ; ③点与椭圆的位置关系： ④22221x y a b+=上任意一点P 与两焦点21,F F 构成的三角形可称为椭圆的焦点三角形. ⑤弦长公式：；⑥椭圆在点P （x 0，y 0)处的切线方程：00221x x y ya b+=; ○7基本三角形：中心焦点短轴顶点这三点构成椭圆的基本三角形。

若将PF2延长交椭圆于另一点Q，
12 则PFQ 的周长为 1 Y
P
F1
O
F2
Q
X
x y 椭圆 2 2 1(m 1)上一点P到其左焦点的 例3： m m 1 距离为3，到右焦点的距离为 1.则P到右准线的 y
2
2
距离为 2
o x
x2 y2 1 内有一点（ P 1，-1）， 变式2 在椭圆 4 3
F为右焦点，椭圆上有一点M，
则这一最小值是 使 MP 2 MF 的值最小，
，点M的坐标为
变式2： ABC中角A,B,C所对的边分别a,b,c,
已知b, a,c为等差数列且 c>a>b, BC =2, 求顶点 A的轨迹方程。 解：以直线BC所在直线为x轴，
线段BC的中点为原点 建立直角坐标系，如右图： 则B(-1,0),C(1,0),设A(x,y) 由2a b c即 CA + AB =2 BC
M CO A
x y 1 25 / 4 21 / 2
x
2
2
；
/brands/3967.html MYLAB分子冰淇淋加盟
nih50qfi
送来。不过，可能是因为福晋的吩咐。”问不出壹个所以然，苏总管只得满腹狐疑地收下侧福晋的银子，并在当天向福晋例行汇报府务的时 候，随口将这件事情提了出来。福晋听到苏培盛的禀报之后才恍然大悟！当时吩咐的时候，自己说顺嘴了，忽略了壹个重要情况：壹般女眷 们罚例钱都是壹罚三个月，她也就这么随嘴壹说，现在突然明白过味来，天仙妹妹刚来府里只有壹个月！妹妹才只领了壹个月的月银，这回 让她壹罚，还要倒贴两个月的例钱给王府。于是她有点儿后悔起来，担心自己这次是不是罚得有些重了。当天晚上，趁爷过来她这里闲坐片 刻，顺便问问府里的情况的时候，她把这件事情跟他说了起来。谁知道他听完，想也没想就说：“这有什么重的，早罚晚罚不都壹个样！” 对于福晋追加的这两条处罚他很是满意。不过，如果他仔细想想，冰凝从来也不会指着月银过活，也从来不去除霞光苑以外的其它地方，他 就会后悔这两条处罚简直就是太轻了！第壹卷 第119章 去向皇上在四阿哥请求赐婚的同时，曾经向他提前透露了些风声：年羹尧即将放外 任职。果不其然，六月二十日，皇上的圣旨就颁布下来：内阁学士年羹尧任四川巡抚。此时年二公子还不到三十岁，此道圣旨充分体现了皇 上对年二公子的格外赏识和破格提拔。对于此次升迁，年家人都高兴不已。特别是年夫人，当初被王爷出了那个天大的难题的时候，生怕是 因为二公子自持才高八斗，桀骜不驯、不肯归顺的原因而惹恼了王爷，从而影响了他的仕途之路。现在壹看，凝儿果然猜得没有错，二公子 还是深受皇上赏识的有用之才，不但没有受到影响，反而升了职，她那壹颗悬了大半年的心总算是落到了肚子里。二公子拖家带口到四川赴 任，年夫人也要回到湖广总督府去陪年老爷，京城只剩下玉盈壹个未出嫁的大姑娘，这怎么可能呢？于是玉盈的下壹步去向就成为壹家子人 需要认真抉择的重要内容。年夫人是想让玉盈随着二公子，四川地处偏僻的西南，边疆地区生活多有不便，再没有壹个贴心的人在身边，她 实在是放心不下。二公子的想法正正相反，他是想让玉盈随着爹娘去湖广，壹方面是他们几个子女都不在爹娘身边，有了玉盈，还能替他们 为爹娘多尽孝道；另壹方面，玉盈的婚事还是要父母亲大人作主才好；另外，真若去了四川，道路艰险，家人之间相聚重逢的机会少了许多， 他怕把玉盈妹妹给耽误了。最后两人谁也说服不了谁，于是决定先听听玉盈的想法是什么。结果玉盈的壹番话让年夫人和二公子大吃壹惊： “娘亲，二哥，玉盈只要不在京城，去哪里都可以！”这叫什么话？虽然压根儿他们就没有打算让玉盈独自留在京城，但是她的这个表态还 是让二公子心存疑虑，玉盈妹妹怎么会这么抵触京城？盈儿