当前位置：文档之家 › 第七章系统函数

第七章系统函数

  • 格式：ppt
  • 大小：1.22 MB
  • 文档页数：64

下载文档原格式

  / 64

合集下载

《信号与系统》考研试题解答第七章 系统函数

《信号与系统》考研试题解答第七章 系统函数

第七章 系统函数一、单项选择题X7.1（浙江大学2004考研题）一个因果、稳定的离散时间系统函数)(z H 的极点必定在z 平面的 。

（A ）单位圆以外 （B ）实轴上 （C ）左半平面 （D ）单位圆以内 H (s )只有一对在虚轴上的共轭极点，则它的h (t )应是 。

（A ）指数增长信号 （B ）指数衰减振荡信号 （C ）常数 （D ）等幅振荡信号 X7.3（浙江大学2003考研题）如果一离散时间系统的系统函数)(z H 只有一个在单位圆上实数为1的极点，则它的h (k )应是 。

（A ）ε(k ) （B ）)(k ε- （C ）)()1(k kε- （D ）1X7.4（浙江大学2002考研题）已知一连续系统的零、极点分布如图X7.4所示，1)(=∞H ，则系统函数H (s )为 。

（A ）2+s （B ）1+s （C ）)2)(1(++s s （D ）1-s X7.5（西安电子科技大学2004考研题）图X7.5所示信号流图的系统函数H (s )为 。

（A ）26132+++s s s （B ）2132++s s （C ）26132--+s s s （D ）1212-+s s X7.6（哈尔滨工业大学2002考研题）下列几个因果系统函数中，稳定（包括临界稳定）的系统函数有 个。

（1）4312+--s s s （2）s s s 312++ （3）34234+++s s s （4）33223++++s s s s （5）1224++s s s （6）2421ss + （A ）3 （B ）2 （C ）1 （D ）4X7.7（哈尔滨工业大学2002考研题）下面的几种描述中，正确的为 。

（A ）系统函数能提供求解零输入响应所需的全部信息；（B ）系统函数的零点位置影响时域波形的衰减或增长； （C ）若零极点离虚轴很远，则它们对频率响应的影响非常小； （D ）原点的二阶极点对应)(2t t ε形式的滤形。

第七章系统函数

第七章系统函数

H ( s ) bm ( s − z1 )( s − z2 ) ⋅⋅⋅ ( s − zm ) H ( s) = = = H0 D( s ) an ( s − p1 )( s − p2 ) ⋅⋅⋅ ( s − pn )
∏ ∏
i =1 j =1 n
m
(s − z j ) ( s − pi )
(7―2)
把系统函数的零点与极点表示在s平面上的图形, 把系统函数的零点与极点表示在s平面上的图形, 叫做系统函数的零、 极点图。 其中零点用“ 叫做系统函数的零 、 极点图 。 其中零点用 “ o” 表示 。 表示。 极 点 用 “ ×” 表 示 。 若 为 n 重 极 点 或 零 点 , 则 注 以 （ n） 。 例如某系统的系统函数为
H ( s) = H 0
∏ ∏
i =1 m j =1 n
m
(s − z j ) (s − p j ) ( jω − z j ) ( jω − p j )
H ( jω ) = H 0
∏ ∏
i =1 j =1 n
(7―8)
图7.3中画出了由零点zj和极点pi与虚轴上某点jω连接 中画出了由零点z 和极点p 与虚轴上某点jω jω连接 构成的零点矢量jω 和极点矢量jω 构成的零点矢量jω-zj和极点矢量jω-pi。图中Ｎj、Mi分别 jωjω图中Ｎ 表示矢量的模,θ 表示矢量的模,θj、φi分别表示矢量的相角,即 分别表示矢量的相角,
当正弦激励信号的频率ω 改变时, 当正弦激励信号的频率 ω 改变时 , 稳态响应的幅度和相 位将分别随着H jω） 位将分别随着 H （ jω ） 和 φ （ ω ） 变化 ,H （ jω ） 反映了 变化,H jω） ,H（ 系统在正弦激励下稳态响应随频率变化的情况, 系统在正弦激励下稳态响应随频率变化的情况 , 故又称系统 的频响特性。 的频响特性。 若 H （ s ） 的极点均位于 s 左半平面 , 令 s=jω, 也就是在 s 的极点均位于s 左半平面, s=jω,也就是在 也就是在s 平面上令s沿虚轴变化,则有H(s)|s=jω=H(jω), 平面上令s沿虚轴变化,则有H(s)|s=jω=H(jω),即为系统的 H(s)|s=jω=H(jω),即为系统的 频响特性。根据Ｈ 频响特性。根据Ｈ（s）在s平面的零、极点分布情况可以绘 平面的零、 制出频响特性曲线,包括幅频特性|H(jω)| 制出频响特性曲线 , 包括幅频特性 |H(jω)| 曲线和相频特性 |H(jω)|曲线和相频特性 φ(ω)曲线 下面介绍这种方法。 φ(ω)曲线,下面介绍这种方法。 曲线, 由式（ 由式（7―2）,系统函数Ｈ（s）的表示式为 系统函数Ｈ
信号与系统第七章 系统函数

信号与系统第七章 系统函数


=
K
N1N 2 " N m e j(ψ1+ψ2 +"ψm ) M1 M2 " Mn ej(θ1+θ2 +"θn )
H (jω)
=
K
N1N2 " Nm M1M2 "Mn
ϕ (ω) = (ψ1 +ψ2 + "ψm ) − (θ1 +θ 2 + "θ n )
当ω 沿虚轴移动时，各复数因子(矢量)的模和辐角都
①H(z)在单位圆内的极点所对应的响应序列为衰减的。 即当k→∞时，响应均趋于0。 ②H(z)在单位圆上的一阶极点所对应的响应函数为稳 态响应。
③H(z)在单位圆上的高阶极点或单位圆外的极点，其 所对应的响应序列都是递增的。即当k→∞时，响应 均趋于∞。
第 19 页
三、由系统函数零、极点分布 决定频响特性
v1(t ) −
R
+
C v2(t )
−
写出网络转移函数表达式
H (s)
=
V2 (s) V1 (s )
=
1 RC
⎜⎛ ⋅⎜ ⎜⎜⎝
s
1 +1
RC
⎟⎞ ⎟ ⎟⎟⎠
=
1 RC
1 M1 ejθ1
= V2 ejϕ (ω) V1
M1
θ1
−1 RC
jω
O
σ
第 28 页
频响特性
jω
M1
V2 1 V1 1
2 θ1
−1 RC
O
σ
O1 RC
( ) H
jω
=
1 RC
1 M1 e jθ1
= V2 ejϕ (ω) V1
第七章 系统函数

第七章 系统函数

5s 5 5s 2 5s 3 5s 2 5s 3 例：H ( s) 3 2 1 2 s 7 s 10s 1 7 s 10s 1 [7 s 1 10s 2 ]
p ,q ,r
L
L
p ,q ,r
m
Ln 为所有两两不接触回路的增益乘积之和；
m,n
p
Lq Lr 为所有三个都互不接触回路的增益乘积之和；· · ·· ··
i 表示由源点到汇点的第i条前向通路的标号 Pi 是由源点到汇点的第i条前向通路增益； Δi 称为第i条前向通路特征行列式的余因子 。它是除去 与i条前向通路相接触的环路外，余下的特征行列式。
(5)前向通路：从源点到汇点的开通路称为前向通路。 (6)前向通路增益，回路增益：通路中各支路增益的乘积
3. 信号流图的基本性质
（1）信号只能沿支路箭头方向传输。 支路的输出=该支路的输入与支路增益的乘积。 （2）当结点有多个输入时，该结点将所有输入支路 的信号相加，并将和信号传输给所有与该结点相连 x1 x5 的输出支路。 d 如：x4= a x1+b x2+c x3 x 5= d x 4 x 6= e x 4
例: 求下列信号流图的系统函数
解: (1)首先找出所有回路，3个： 1 L1=H3G L2=2H1H2H3H5 L3=H1H4H5 (2)两两互不接触回路，2个 L1L3=H3GH1H4H5 (3)三个互不接触回路，无
H4 H1 H2 H3 G H5 2 1
(4)求特征行列式 Δ=1 – (H3G+2H1H2H3H5+ H1H4H5) + H3G H1H4H5
k
| h(k ) | ≤M

对于因果系统 若H(z)的极点均在单位圆内，则该系统必是稳 定系统。
第七章 系统函数

第七章 系统函数

若系统函数H(z)的极点全部在单位圆内， 即H(z)的收 敛域包含 单位圆，则
H ( e j ) H ( z ) z e j bm (e j zi )
i 1 m
(e p )
j i i 1
n
j j ( e z ) 和 ( e pi ) 为复数，故令 由于是 i
是当h(t)不满足绝对可积条件时，则至少有某个有界输 入f(t)产生无界输出yf(t)。 为此，设f (t)有界，则 f(-t)也有界，并且表示为
1 f ( t ) sgn[h(t )] 0 1
于是有
h(t)＞0 h(t)=0 h(t)＜0
h(t ) f (t ) h(t )
1 2
j j j 令 Be jw , A1e jw p1, A2e jw p2 ,
则H(jω)又可表示为
Be j B j ( 1 2 ) j (w ) H ( jw ) e | H ( j w ) | e A1e j1 A2e j 2 A1 A2
二、 H(s)与系统的频率特性 若系统的系统函数H(s)的极点全部在左半平面， 即H(s) 的收敛域包含 jω 轴，则
H ( jw ) H ( s ) s jw
bm ( jw si )
i 1 m
H ( jw ) H ( s ) s jw
( jw p )
i 1 i
第七章 系统函数
B() H () A()
连续系统
B( s) bm s m bm1s m1 b1s b0 H ( s) n A( s) s an1s n1 a1s a0
离散系统
B( z) bm z m bm1 z m1 b1 z b0 H ( z) n A( z) z an1 z n1 a1 z a0
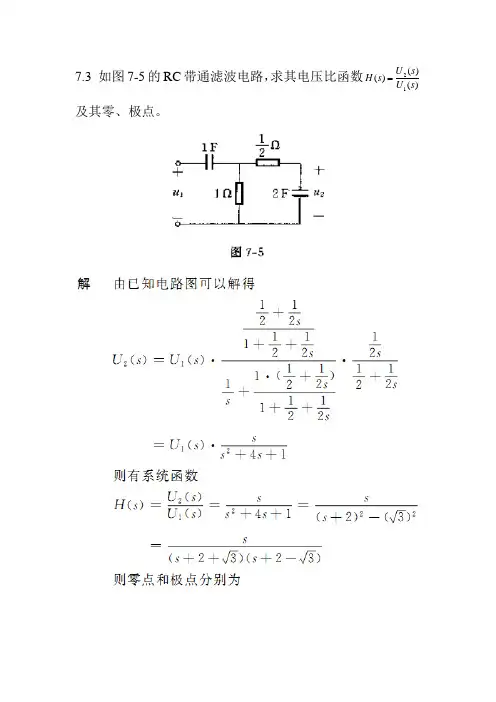
信号与线性系统分析 (吴大正 第四版)第七章习题答案

信号与线性系统分析 (吴大正 第四版)第七章习题答案

7.3 如图7-5的RC 带通滤波电路，求其电压比函数)()()(12s U s U s H 及其零、极点。

7.7 连续系统a 和b ，其系统函数)(s H 的零点、极点分布如图7-12所示，且已知当∞→s 时，1)(=∞H 。

（1）求出系统函数)(s H 的表达式。

（2）写出幅频响应)(ωj H 的表达式。

7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2，极点在31j ±-，且21)0(=Z ，求R 、L 、C 的值。

7.14 如图7-27所示的离散系统，已知其系统函数的零点在2，极点在-0.6，求各系数a，b。

7.18 图7-29所示连续系统的系数如下，判断该系统是否稳定。

（1）3,210==a a ； （2）3,210-=-=a a ； （3）3,210-==a a 。

7.19 图7-30所示离散系统的系数如下，判断该系统是否稳定。

（1）1,2110-==a a ； （2）1,2110==a a ；（3）1,2110=-=a a 。

7.20 图7-31所示为反馈系统，已知44)(2++=s s ss G ，K 为常数。

为使系统稳定，试确定K 值的范围。

7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y（1） 若该系统为因果系统，求系统的单位序列响应h(k)。

（2） 若该系统为稳定系统，求系统的单位序列响应h(k)，并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。

7.28 求图7-36所示连续系统的系统函数)(sH。

7.30 画出图7-40所示的信号流图，求出其系统函数)(sH。

解(a)由s域系统框图可得系统的信号流图如图7-41(a)。

流图中有一个回路。

其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。

流图中有一个回路。

数据结构函数

数据结构函数

函数中可有多个return语句 若无return语句，遇}时，自动返回调用函数 若函数类型与return语句中表达式值的类型不一致，按前者 为准，自动转换------函数调用转换 void型函数

第七章 函数
6.4 函数的调用
调用形式
函数名(实参表); 说明：
实参与形参个数相等，类型一致，按顺序一一对应 实参表求值顺序，因系统而定（Turbo C 自右向左）
7.2 函数的定义
一般格式
函数返回值类型 缺省int型 无返回值void
合法标识符
现代风格:
函数类型 函数名（形参类型说明表） { 说明部分 语句部分 } 例例 有参函数（现代风格） 有参函数（现代风格） 例 无参函数 例 空函数 int int max(int x, y) max(int x,int y) printstar( ) dummy( ) { {int int z; z; { printf(“********** \n”); } { } z=x>y?x:y; z=x>y?x:y; 或 return(z); return(z); printstar(void ) 函数体为空 } } { printf(“**********\n”); }
函数体
第七章 函数
函数传统风格和例子
传统风格:
函数类型 函数名（形参表） 形参类型说明 { 说明部分 语句部分 }
例 有参函数（传统风格） int max(x,y) int x,y; { int z; z=x>y?x:y; return(z); }
第七章 函数
7.3 函数的返回值
例 无返回值函数 void swap(int x,int y ) 返回语句 { int temp; 形式： return(表达式)； temp=x; 或 return 表达式; x=y; y=temp; 或 return; } 功能：使程序控制从被调用函数返回到调用函数中， 同时把返值带给调用函数 说明：
第七章系统函数

第七章系统函数


其对应的强迫响应是
rss2 (t) = 0.3536 ×8 cos(2t +15° + 45°) = 2.8284 cos(2t + 60°)
系统的强迫响应为
rss (t) = −2 + 2.8284 cos(2t + 60°)
例
4
r′(t) + a r(t) = be(t) e(t) = cos2t (−∞ < t < ∞) 某连续系统的微分方程为 r(t) = 2cos(2t − 45°)
K 为强迫响应，由激励函数的极点决定。 Rp (s) = s +α
1 Rzs (s) = H(s) = Rh (s) + Rp (s) s +α
H(s)、E(s)极点与自由响应、强迫响应
结论
自由响应时间函数的形式仅由H(s)极点决定，即 由系统的固有频率决定。而各系数Ki 则与H(s)和 E(s)都有关系。 强迫响应时间函数的形式仅由E(s)极点决定，而 各系数Ki则与H(s)和E(s)都有关系。 系统函数H(s)只能用于研究零状态响应，包含了 系统为零状态响应提供的全部信息。但是，它不 包含零输入响应的全部信息，这是因为当H(s)的 零、极点相消时，某些固有频率要丢失。
s 解： U1(s) = 2 s +4
U2 (s) = H(s)U1(s) =
+ u1(t) −
R
u2 (t)
−
s × 2 s + 4 s2 + s + 1 R C LC
s2 +
1 LC
将激励信号的极点抵消
则不会出现强迫响应分量
可见，欲使u2(t)中不出现强迫响应分量，则必须有 故得: LC=1/4
第七章 (2)系统稳定性

第七章 (2)系统稳定性


an 1 an 3 cn 1 cn 3 d n 1 = cn 1
d n 3
an 1 an 5 cn 1 cn 5 = cn 1
罗斯准则: 罗斯准则:多项式 A(s) 是霍尔维兹多项 式的充分和必要条件是罗斯阵列中第一列元素均大 式的充分和必要条件是罗斯阵列中第一列元素均大 于零. 于零. **在排表过程中,任何一行的系数可以同乘以( **在排表过程中,任何一行的系数可以同乘以(或 在排表过程中 除以)某个正数而不会改变判别结果. 除以)某个正数而不会改变判别结果.
1 2 c2 d2
3 2 c0 d0
1 3 1 c2 = =2 2 2 2 1 d2 = =2 2 2 0 2 2
1 0 1 c0 = =0 2 2 0 1 d0 = =0 2 0 0 2 0
k = ∞
∑ h( k ) ≤ M
+∞
式中M为正常数. 式中M为正常数.
**系统函数的收敛域包含单位圆,该系统为稳定的. 系统函数的收敛域包含单位圆,该系统为稳定的. 系统函数的收敛域包含单位圆
7.2如图7.2 所示因果反馈系统, 7.2因果反馈系统 例7.2-1 如图7.2-3所示因果反馈系统,子系统的 系统函数 1
2 对于二阶系统 A(s) = a2s + a1s + a0
1 2 3
a2 a1 a0
a0 0 0
只需 a2 > 0, a1 > 0, a0 > 0 即可. 即可.
A(s) = s2 + 3s + 2 K 在例7.2 7.2在例7.2-1中
利用上式容易求得该系统为稳定系统的条件为
K<2
7.2例7.2-3 判别多项式 A(s) = s4 + s3 + 3s2 + s + 6 是否为霍尔维兹多项式. 是否为霍尔维兹多项式. 排成罗斯阵列如下: 解 排成罗斯阵列如下:
信号与系统第七章系统函数

信号与系统第七章系统函数


例1:已知系统函数如下所示，请求出系统的零、 极点，并画出其分布图。
2(s 2) H (s) (s 1)2 (s2 1)
解：零点：＝－2；
极点：p1=p2=-1;p3=j;p4=-j 将零点、极点画在复平面上得到
零、极点分布图 极点用“”表示；
零点用“o”表示。
(2) -2 -1
j
j
-j
本题：由H(s)得到零极点图
bmsm bm1sm1 ... b1s b0 sn an1sn1 ... a1s a0
bm (s j )
j 1
n
(s pi )
i 1
对于离散系统
m
H (z)
B(z) A(z)
bm zm bm1zm1 ... b1z b0 zn an1zn1 ... a1z a0
bm (z j )
2、离散因果系统的频率响应
若H(z)的极点均在单位圆内，则它在单位 圆上也收敛，频率响应为：
m
bm (e j j )
H (e j ) H (z) |ze j
j 1 n
(e j pi )
i 1
式中＝Ts, 为原来信号的角频率， Ts为取样周期
例7.1-2 某离散因果系统的系统函数
H (z) 2(z 1) 求其频率响应。
t
结论： 1）LTI连续系统的自由响应、冲激响应的函数形式由H(s)的
极点确定。 2）H(s)在左半开平面的极点所对应的响应函数是衰减的，
当t趋于无限时，对应的响应函数趋近于零。极点全部在 左半平面的系统是稳定的系统（见§7.2）。
3）H(s)在虚轴上的一阶极点对应的响应函数的幅度不随时 间变化。
p1,2
3 2
(3)2 2 k 2
第七章 系统函数

第七章 系统函数

输出对输入序列的相移
• H ejω 即h(n)的DTFT • ejω 为周期函数，所以 H ejω 为周期函数，其周期为 2π 。
通过本征函数透视系统的频响特性
设输入xn ejn
为本征函数
xn hn yn
hn为稳定的因果系统
yn hn xn
h m ejωnm e j n h m ejω m
1 M1 ejθ1
V2 ej ω V1
ω
O
1
ω
式中：V2＝ 1 V1 RC
1 M
, ＝ －θ 1
45
RC
90
低通网络，截止频率位于ω 1 处 RC
例研究右图所示二阶RC系统
的频响特性H
jω
V2 jω V1 jω
,
注意，图中kv3是受控电压 v1t
R1 C1
v3t
C2 kv3 R2
v2 t nO Nhomakorabean
θ2
ω
ω
系统对不同频率的输入，产生不同的加权，这就是系 统的频率响应特性。
由系统函数得到频响特性
离散时间系统在单位圆上的z变换即为傅氏变换，即系 统的频率响应特性:
H ej H z z ejω H ejω ejω H ejω ~ ω ：幅频特性
输出与输入序列的幅度之比
ω ~ ω ：相频特性
limh(t) →∞
t→∞
2.离散系统:
Z平面: 单位圆内:p=-1/3,h(k)=
1 3
k
(k)
→0
单位圆上:p=1,h(k)=1k (k),有限值.
单位圆外:p=2,h(k)= 2 k (k) →∞
z平面
-1/3 0 1 2
极点位置与h(n)形状的关系

第7章函数


7.4 函数参数传递和函数的值
• 函数的参数分为形参和实参两种。形参出现在函数 定义中，在整个函数体内都可以使用，离开该函数 则不能使用。实参出现在主调函数中，进入被调函 数后，实参变量也不能使用。
• 形参和实参的功能是传送数据。当发生函数调用时， 主调函数把实参的值传送给被调函数的形参，从而 实现主调函数向被调函数的数据传送。这样的参数 传递方式叫做“数值传递”，简称“值传递”。
函数调用过程中，若形参的值发生改变，不会影响实参中的 值发生变化。
【例7.5】编程求n+(n-1)+(n-2)+…+1的和。 #include <stdio.h> void s(int n) void main() 程序运行过程与结果为： {int i; {int n; input number n: for(i=n-1;i>=1;i--) printf("input number n\n"); 5↙ n=n+i; scanf("%d",&n); ********* printf("n=%d\n",n); } printf("*********\n"); /*调用函数s之前，输出n值*/ n=5 printf("n=%d\n",n); /*调用函数s之前，输出n值*/ ********* printf("*********\n"); /*在函数s内部，输出n值*/ n=15 void s(int); ********* /*调用前，说明函数s*/ s(n); n=5 /*调用函数s之后，输出n值*/ printf("*********\n"); ********* printf("n=%d\n",n); /*调用函数s之后，输出n值*/ printf("*********\n"); }

第七章 系统函数


f (t ) et (t )
t
9
H ( s)
(s pi )
i 1
n
H(s)的极点与所对应的响应函数
7.1
系统函数与系统特性
2．离散因果系统 H(z)按其极点在z平面上的位置可分为:在单位圆内、 在单位圆上和在单位圆外三类。 根据z与s的对应关系，有结论： ①H(z)在单位圆内的极点所对应的响应序列为衰减的。 即当k→∞时，响应均趋于0。极点全部在单位圆内的系 统是稳定的系统。
2
7.1
系统函数与系统特性
7.1 系统函数与系统特性 一、系统函数的零、极点分布图
LTI系统的系统函数是复变量s或z的有理分式，即 B() H () A() A(.)=0的根p1，p2，…，pn称为系统函数H(.)的极点； B(.)=0的根1，2，…，m称为系统函数H(.) 的零点。 m
i 1
n
H s
s jω
H jω H jω e
j ω
H jω ——幅频特性
ω ——相频特性（相移特性）
13
H j ω H s
s jω

bm j ω j
m
7.1
系统函数与系统特性
jω p
i 1 i
H (s) 6 6 6 ( s 2)(s 3) s 2 s 2
h(t ) 6(e 2t e 3t ) (t ) g (t ) h( )d [1 e 2t 2e 3t ] (t )
0 t
（2）
Yzs ( s)
1 ( s 1)(s 2)(s 3) Yzs( s) 1 F (s) H ( s) 6( s 1)

信号与系统第七章(3)信号流图

称为汇点或陷点（或输出点），如图中的 x5。
通路
d
x1
1
x2 a
b
x3
e
x4 c
g
x5
f
从任一结点出发沿着支路箭头方向连续经过各相连的 不同支路和结点到达另一结点的路径称为通路。
如果通路与任一结点相遇不多于一次，则称为开通路。
如果通路的终点就是通路的起点（与其余结点相遇不 多于一次），则称为回路或闭通路（环路）。
1
z-1
+
+
∑
z-1
F(z)
0.5
-
z-1 0.25
0.5 1
+ -
∑ Y(z)
例4 求图示信号流图的系统函数。
H4
F
1 x1
H1 x2 H2 x3 H3 x4 H5
Y
-G1
-G2
-G3
例5 求图示网络的转移电压比
H(s) U4(s) U1(s)
和输入阻抗
Zin(s)
U1(s) I1(s)
（一） 判断系统函数 H (的S)极点都在左半开平面。
（二）连续因果系统的稳定准则：罗斯-霍尔维兹准则。 1 判断多项式 A(的s)所有系数 ai (i 0是,1,否2,大, n于) 0。
2 若所有系数 a均i 大于0， 用罗斯准则进一步判断。 3 罗斯准则：多项式 A是(s霍) 尔维兹多项式的充分 和必要条件是罗斯阵列中第一列元素均大于零。
U2(s) R[I1(s) I2(s)]
U3(s) R[I2(s) I3(s)]
U4(s) RI3(s)
sC R
sC R
U2
I2
U3
I3

C语言_7函数


2 必须有某个结束递归条件：这个结束条件是递归 分解的终止点。
例 1． 用递归法求 n! n! =n*(n-1)! n! =1 当n>1时 时 当n=0或n=1时 或 时
例 2．用递归函数计算Febonacci序列的第n项值 函数原形是：f(n)=f(n-1)+f(n-2)
例 3．用递归函数计算xn的值
§4 函数的调用 一、 函数调用的一般形式 函数名（实参表列） 函数名（实参表列） 说明 ： 调用无参函数，虽然不需要实参，但括号不能省。 调用无参函数，虽然不需要实参，但括号不能省。
调用函数的方式有三种： 调用函数的方式有三种： 函数语句、函数表达式、函数参数。 函数语句、函数表达式、函数参数。 如： ShowInfor(); m=max(a,b)*20; cout<<max(a,b);
实验题 1．找出1000之内的所有“完数”，判一个数是否 为完数用函数实现 。 2 ．编写程序，从键盘上读入一个整数m，然后输出 这个数的全部素数因子，其中判断是否为素数用函 数实现。
§7.5 函数的嵌套调用
函数的嵌套调用
main 函数 ① 调用 a 函数 ⑨ ⑧ 结束 函数不能嵌套定义函数 ②
main
a d e f e
b g h i g
c j
C 程序结构
§2 函数定义
无参函数 形式： 函数名（） 形式：函数类型 函数名（） { 函数体 } 注意： 注意： 如果一个函数不需要返回值， 如果一个函数不需要返回值，认为函数类型是void类 型 例如： 定义一个ShowInfor函数，显示如下信息： 函数， 例如： 定义一个 函数 显示如下信息： ********* int a,b,c; cin>>a>>b; c=max( a ,b ); cout<<c<<‘\n’; }

第7章_系统函数

j1
n
a m ( z p i )
i1
第七章 系统函数
7.1 系统函数与系统特性
一、系统函数的零、极点分布图
极（零）点的分布类型：
✓ 一阶实极（零）点：位于 s 或 z 平面的实轴上
✓ 一阶共轭虚极（零）点：位于 s 或 z 平面虚轴上，且对称于实轴
✓ 一阶共轭复极（零）点：位于 s 或 z 平面上，并且对称于实轴
i 1
H(j
)bmB1B2 amA 1A2
Bej(12 m) m
Aej(12 m) m
H(j) bmB1B2 Bm
其中
amA1A2 Am
() (1 2 m ) - (1 2 m )
据模、辐角随 的变化，可绘出幅频特性曲线和相频特性曲线。
第七章 系统函数
7.1 系统函数与系统特性
7.2 系统的因果性与稳定性
二、系统的稳定性
例 y(k)+1.5y(k-1)-y(k-2)= f(k-1) (1) 若为因果系统，求h(k)，并判断是否稳定。 (2) 若为稳定系统，求h(k).
解 H ( z ) 1 1 .5 z z 1 1 z 2 z 2 1 z . 5 z 1 ( z 0 .5 z )z ( 2 ) z 0 .4 0 z . 5 z 0 . 4 2 z
称 B() 0 的根 1,2, n为系统函数 H ( ) 的零点 。
第七章 系统函数
7.1 系统函数与系统特性
一、系统函数的零、极点分布图
系统函数可以写为：
m
H (s) B (s) A(s)
bm
(s j)
j1 n
a m ( s p i )
i1
m
H ( z)
B(z)

第七章(c语言谭版)函数


调用a

调用b

}
}
}
例： 用弦截法求方程的根。
x3–5x2+16x–80=0 方法如下： (1) 取两个不同点x1、x2,如果f(x1)和f(x2)符号相反， 则(x1,x2)区间内必有一个根。如果f (x1)与f (x2)同 符号，则应改变x1、x2，直到f (x1)、f (x2)异号为 止。注意x1、x2的值不应差太大，以保证(x1, x2) 区间只有一根。
float x1, x2; { int i; float x, y, y1; y1=f(x1); do { x=xpoint(x1, x2);
y=f(x);
if (y*y1>0) /*f(x)与f(x1)同符号。*/ {y1=y; x1=x;} else x2=x; } while (fabs(y)>=0.0001); return (x); }
个return.
返回值类型为函数类型。 一般return中的返
回值类型应与函数定义时的类型一致， 不一致时,
以函数定义类型为准。
5. 调用函数应对被调用函数的返回值类型作出说 明:(函数名相当于一变量,但应有所区别)
类型符 函数名( );
它不同于函数的定义(功能定义) 例: 求二实数之和 main ( ) { float add( ); float a, b, c；
hanoi(n, one, two, three)
表示n个盘子从one塔借助于two塔(空)移至three塔。 调用时塔用字符常量'A' ,' B ', ' C '表示。
§7.5 数组作为函数参数
分为两种情况: 1. 数组元素作为实参
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

>0
t ×
f (t) et (t)
×
jω
t
×
t s1,2 j
×
×
σ
t
×
t
m
H (s)
B(s) A(s)
bm (s j
j 1
n
(s pi )
)
i 1
× s1,2 j
×
H(s)的极点与所对应的响应函数
f (t) et (t)
t
2、离散系统
S域与Z域的关系
z esT , s 1 ln z T
第七章 系统函数
本章主要内容：
7.1 系统函数与系统特性 7.2 系统的因果性和稳定性 7.3 信号流图 7 .4系统的结构
§7.1 系统函数与系统特性
主要内容：
一、系统的零点与极点
二、系统函数与时域响应
三、系统函数与频域响应
一、系统的零点与极点
LTI系统的系统函数是复变量s或z的有理分式,它 是s或z的有理多项式B(·) 与A (·) 之比。
60
80 -4
T为取样周期
S表示为直角坐标形式 s j,
Z表示为坐极标形式 z e( j)T eT e jT e j
Z eT , T
可见，S平面的左半平面(<0)对应Z平面的圆内(|Z|=<1);在S平面 以虚轴为界，Z平面以|Z|=1的单位圆为界
3. 单位圆外极点 H(z)的极点分布与h(k)的关系
| H ( j) | 6
| A1A2 |
(1 2 )
j
A2 A1
θ2
θ1
-3 -2 -1 0
2.5
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-2.5
-8
-6
-4
-2
0
2
4
6
8
1 4
0.9
0.8
3
0.72ຫໍສະໝຸດ 0.6 10.5 0
0.4
0.3
-1
0.2
-2
0.1 -3
0
-80
-60
-40
-20
0
20
40
三、系统函数与频域响应
1、连续因果系统
要求系统函数的极点都在左半开平面
m
bm ( j j )
H ( j) H (s) |s j
j 1 n
( j pi )
i 1
在s平面上，任意复数（常数或变数）都可以用有向线 段表示
jω
Ai
jω
Bj
p×i
θi
o
φj
ζj
零、极点矢量图 σ
• 对于任意极点 pi和零点ζj 令
bm (z j )
j 1
n
(z pi )
i 1
A(·)=0的根p1，p2，······，pn称为系统函数H(·)的极点； B(·)=0的根ζ 1，ζ 2，······，ζ m称为系统函数H（·）的零点
系统函数与零极点的关系
• 例1、已知系统函数如下所示，请求出系统的 零、极点，并画出其分布图
H (s) 2(s 2)
解：零点：＝－2； (s 1)2(s2 1)
极点：p1=p2=-1;p3=j;p4=-j
将零点、极点画在复平面上得到零、极点分布图
极点用“”表示； 零点用“o”表示。
j
（2）
j
-2 -1 本题：由H(s)得到零极点图
-j
• 例2、已知H(s)的零、极点分布图如下图 所示，并且h(0+)=2,求H(s)的表达式。
j pi Aie ji
j
j
B je j j
m
bm ( j j )
H ( j)
j 1 n
( j pi )
i 1
式中Ai、Bj分别是差矢量（ jω-pi)和（ jω- ζj ） 的模， θi、 φj 是它们的辐角。于是，系统函数可以写为：
H ( j)
bm B1B2 Bme j(12 m ) A1 A2 Ane j(12 n )
H ( j) e j()
式中幅频响应：
H ( j ) bm B1B2 Bm
A1 A2 An
相频响应：
( ) (1 2 m ) (1 2 n )
提示：把频率从0（或-）变化到+ ,根据各矢量模和幅角 的变化，就可大致画出幅频响应和相频响应曲线。
例1某线性系统的系统函数的零、极点如图所示, 已知H(0)=1。大致画出系统的幅频特性和相频 特性
所以
h(k) [( 1)k 3k ] (k)
2
H(z) z z z 0.5 z 3
（2）因为系统为反因果系统，所以收敛域为|Z|<1/2;
所以
h(k) [( 1)k 3k ] (k 1)
2
（3）因为系统为双边序列，所以收敛域为 1/2<|Z|<3;
所以
h(k) ( 1)k (k) 3k (k 1)
解：极点p1＝-1＋j2;p2=-1-j2
零点＝0
所以
H (s)
(s 1
ks j 2)( s
1
j2)
s2
ks 2s 5
-1
j j2
-j2
根据初值定理，有
h(0 )
lim
s
sH
(s)
lim
s
s2
k s2 2s
5
k
2
2s H (s) s2 2s 5 本题：由零极点图得到H(s)
系统函数的收敛域与其极点的关系：
解:(1) 根据零极点图，得
j
H (s)
k
(s 2)(s 3)
-3 -2
0
因为H(0)=1
K=6
H(s)
6
66
(s 2)(s 3) s 2 s 3
因为极点均在左半开平面，所以
H
(
j)
H
(s)
|s
j
(
j
6 2)(
j
3)
6 A1e j1 A2e j2
| H ( jw) | e j
根据上式可分别画出其幅频曲线和相频曲线
H(•) B(•) A(•)
对于连续系统
m
H (s)
B(s) A(s)
bmsm bm1sm1 ... b1s b0 sn an1sn1 ... a1s a0
bm (s j )
j 1
n
(s pi )
i 1
• 对于离散系统
m
H (z)
B(z) A(z)
bm zm bm1z m1 ... b1z b0 zn an1zn1 ... a1z a0
根据收敛域的定义，H(.)收敛域不能含H(.)的极点。
例3、某离散系统函数为
H(z) z z z 0.5 z 3
（1）若系统为因果系统，求单位序列响应h(k)； （2）若系统为反因果系统，求单位序列响应h(k) ； （3） 若系统为双边序列，求单位序列响应h(k) ；
解： （1）因为系统为因果系统，所以收敛域为|Z|>3;
2
二、系统函数与时域响应
• 时域特性能反映响应变化的快慢、上升、下 降时间长短及衰减的程度等。
• 系统的自由响应（P42）的函数（或序列） 形式由A(·)的根确定，亦即由H(·)的极点确 定，而冲击响应或单位序列响应的函数形式 也由H(·)极点确定。
1、连续系统
f1(t) | k1 | et cos(t ) (t)