信号与线性系统分析(吴大正第四版)第七章习题答案

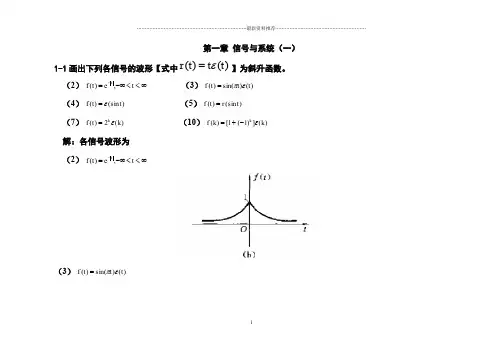
第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t（5）)trf=(sin)(t（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

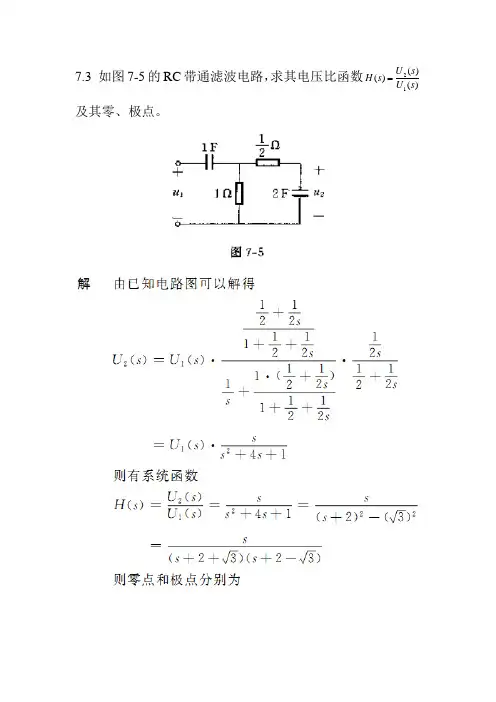
7.3 如图7-5的RC 带通滤波电路，求其电压比函数)()()(12s U s U s H 及其零、极点。

7.7 连续系统a 和b ，其系统函数)(s H 的零点、极点分布如图7-12所示，且已知当∞→s 时，1)(=∞H 。

（1）求出系统函数)(s H 的表达式。

（2）写出幅频响应)(ωj H 的表达式。

7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2，极点在31j ±-，且21)0(=Z ，求R 、L 、C 的值。

7.14 如图7-27所示的离散系统，已知其系统函数的零点在2，极点在-0.6，求各系数a，b。

7.18 图7-29所示连续系统的系数如下，判断该系统是否稳定。

（1）3,210==a a ； （2）3,210-=-=a a ； （3）3,210-==a a 。

7.19 图7-30所示离散系统的系数如下，判断该系统是否稳定。

（1）1,2110-==a a ； （2）1,2110==a a ；（3）1,2110=-=a a 。

7.20 图7-31所示为反馈系统，已知44)(2++=s s ss G ，K 为常数。

为使系统稳定，试确定K 值的范围。

7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y（1） 若该系统为因果系统，求系统的单位序列响应h(k)。

（2） 若该系统为稳定系统，求系统的单位序列响应h(k)，并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。

7.28 求图7-36所示连续系统的系统函数)(sH。

7.30 画出图7-40所示的信号流图，求出其系统函数)(sH。

解(a)由s域系统框图可得系统的信号流图如图7-41(a)。

流图中有一个回路。

其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。

流图中有一个回路。

第一章信号与系统（二）1-1画出下列各信号的波形【式中r(t)t（t）】为斜升函数。

(2)f(t) et t（3）f(t)sin( t) (t)(4)f (t) (sint)（5）f(t)r(sin t)(7)f(t) 2k (k)（10f(k) [1 ( 1)k] (k)）解：各信号波形为（2）f（t） e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。

(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。

1-4写出图1-4所示各序列的闭合形式表达式。

1-5判别下列各序列是否为周期性的。

如果是，确定其周期。

Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示，画出下列各函数的波形。

(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解：各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示，画出下列各序列的图形。

目　录第1章　信号与系统1.1　复习笔记1.2　课后习题详解1.3　名校考研真题详解第2章　连续系统的时域分析2.1　复习笔记2.2　课后习题详解2.3　名校考研真题详解第3章　离散系统的时域分析3.1　复习笔记3.2　课后习题详解3.3　名校考研真题详解第4章　傅里叶变换和系统的频域分析4.1　复习笔记4.2　课后习题详解4.3　名校考研真题详解第5章　连续系统的s域分析5.1　复习笔记5.2　课后习题详解5.3　名校考研真题详解第6章　离散系统的z域分析6.1　复习笔记6.2　课后习题详解6.3　名校考研真题详解第7章　系统函数7.1　复习笔记7.2　课后习题详解7.3　名校考研真题详解第8章　系统的状态变量分析8.1　复习笔记8.2　课后习题详解8.3　名校考研真题详解第1章　信号与系统1.1　复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象，其图像为信号的波形。

根据信号的不同特性，可对信号进行不同的分类：确定信号与随机信号；周期信号与非周期信号；连续时间信号与离散时间信号；实信号与复信号；能量信号与功率信号等。

二、信号的基本运算1加法和乘法f1（t）±f2（t）或f1（t）×f2（t）两信号f1（·）和f2（·）的相加、减、乘指同一时刻两信号之值对应相加、减、乘。

2．反转和平移（1）反转f（－t）f（－t）波形为f（t）波形以t＝0为轴反转。

图1-1（2）平移f（t＋t0）t0＞0，f（t＋t0）为f（t）波形在t轴上左移t0；t0＜0，f（t＋t0）为f（t）波形在t轴上右移t0。

图1-2平移的应用：在雷达系统中，雷达接收到的目标回波信号比发射信号延迟了时间t0，利用该延迟时间t0可以计算出目标与雷达之间的距离。

这里雷达接收到的目标回波信号就是延时信号。

3．尺度变换f（at）若a＞1，则f（at）波形为f（t）的波形在时间轴上压缩为原来的；若0＜a＜1，则f（at）波形为f（t）的波形在时间轴上扩展为原来的；若a＜0，则f（at）波形为f（t）的波形反转并压缩或展宽至。

7-1解 对于（a)图 (1）流图性质简化：21bx E x +=312dx ax x +=()32dx bx E a ++= ⇒ abdx aE x -132+=123ex cx x +=()22bx E e cx ++=()abdx aE be c eE -13+++=()()ab aE be c eE ab d be c x ---1113++=⎪⎭⎫⎝⎛+ R x =3所以 bedcd ab ace bed cd ab bea ac abe e E R H -------11+=++==（2)按梅森公式：图（a)有三个环路,环路增益为：edb cd ab 所以ebd cd ab ---1=∆图（a ）有二条前向通路,通路增益为ac e ，且与各环路都相接触,即各特征行列式的余子式都为1，1=i ∆ 。

所以按梅森公式bedcd ab ace E R H ---1+==对于图(b ） （1)流图性质简化:221dx bE x +=()221112dx bE c aE cx aE x ++=+= ⇒ cdcbE aE x -1212+=2ex R = 所以 11-ae H cd =21-cbeH cd= （2）按梅森公式：图(b ）有一个环路，环路增益为：cd对输入1E 有一条前向通路,通路增益为ae ，所以11-aeH cd =对输入2E 有一条前向通路，通路增益为cbe ，所以21-cbeH cd=7—2解()()()()()()()()()⎪⎩⎪⎨⎧++=++=t e t e t t t t e t e t t 21212211142783λλλλλ--()()()t t t r 1132λλ+=7—3解（1）模拟框图：题7—3解图1状态方程与输出方程：()()()()()()⎩⎨⎧+=+=+n e n n n n n 21221311λλλλλ-- ()()n n y 1λ= （2）模拟框图：题7-3解图2状态方程与输出方程：()()()()()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧++=+=+=+=+4-3-4-2-7-3-111143214433221n e n e n n n n n n n n n n n λλλλλλλλλλλ ()()()()()()()()4-3-4-2-7-3-143214n e n e n n n n n n y ++=+=λλλλλ7—4解（1)系统函数可以改写为子系统相乘和相加形式如下()⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛++⨯⨯=5121115s s s s H -， ()53426521++++=s s s s H - 由上两式可以画出级联和并联形式流图()t e 1-()t 1-1-（a ）()t e ()t r （b ）题7—4解图1(2）系统函数可以改写为子系统相乘和相加形式如下()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++=41311111s s s s H -- ()438323161+++++=s s s s H -- 由上两式可以画出级联和并联形式流图()t e 1-()t 1-1-（a)()t e ()t r 1-（b ）题7—4解图27—5解（a ）两条前向通路,三个环路，通路和环路间都接触.41321521413211H H H H H H H H H H H H H H ---+=（b)一条前向通路，三个环路,通路与所有环路都接触，有两个不接触环路。

信号与系统习题解析C1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t（5）)trf=(sin)(t（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f（5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

第一章 信号与系统1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （4）k j k f 34e )(π= （5）)sin(2cos 3)(5t t t f π+=1-6 已知信号)(t f 的波形如图1-6所示，画出下列各函数的波形。

（5）)21(t f - （7）dtt df )( （8）dx x f t⎰∞-)(解：1-7 已知序列)(k f 的图形如图1-7所示，画出下列各序列的图形。

（1）)()2(k k f ε- （3）)]4()()[2(---k k k f εε1-10 计算下列各题。

（5）dt t tt )2()]4sin([2++⎰∞∞-δπ（6）dt t )2()2t (2δ⎰∞∞-+（7）dt t t t )1()12t 2('23-+-+⎰∞∞-δ1-23 设系统的初始状态为)0(x ，激励为)(⋅f ，各系统的全响应)(⋅y 与激励和初始状态的关系如下，试分析各系统是否是线性的。

（1）⎰+=-ttdx x xf x e t y 0)(sin )0()( （2）⎰+=tdx x f x t f t y 0)()0()()(1-23 设系统的初始状态为)0(x ，激励为)(⋅f ，各系统的全响应)(⋅y 与激励和初始状态的关系如下，试分析各系统是否是线性的。

（1）⎰+=-ttdx x xf x e t y 0)(sin )0()( （2）⎰+=tdx x f x t f t y 0)()0()()(1-27 某LTI 连续系统，其初始状态一定。

已知当激励为)t (1y 时，其全响应为0)cos()(1≥+-=t t t e t y π若初始状态不变，当激励为)(2t f 时，其全响应为0)cos(2)(2≥=t t t y π，若初始状态不变，当激励为)(3t f 时，求其全响应。

第二章2-1 已知描述系统的微分方程和初始状态如下，试求其零输入响应。

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t （7）)t(k=f kε)(2（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t（7）)t=(kf kε(2)（10）)f kεk=(k+-((])1)1[1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第2讲第一章信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t （5）)f=t(sin)(tr（7）)(2)(k t f k ε=（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

第7章系统函数一、填空题1．若某信号f（t）的单边拉氏变换为，请写出该信号的傅里叶变换。

【答案】【解析】如果F（s）在虚轴上有k 重w 0的极点，由公式得该信号的傅里叶变换1(1)0021()()()(1)!k k s jw K j F s w w j w k w πδπδ--='+-=-+-。

2．为使线性时不变离散因果系统是稳定的，其系统函数H（s）的极点必须在s 平面的。

【答案】左半平面【解析】因果系统的z 域在极点右面，稳定系统的z 域必须包括虚轴，所以极点在左半平面。

3．离散系统的信号流图如图7-1所示，则H（z）＝＝。

图7-1【答案】【解析】根据信号流图4．线性时不变离散因果系统的系统函数，判断系统是否稳定（填是或否）。

【答案】是【解析】21()(0.1)(0.5)z z H z z z ++=--其极点为120.1,0.5ρρ==，因为两极点均在单位圆之内，故系统是稳定系统。

二、分析计算题1．描述线性非时变系统的微分方程为（1）写出系统函数H（s）的表达式；（2）欲使系统稳定，试确定k 的取值范围。

答：（1）时域到频域2()(2)()6()3()s Y s k Y s Y s X s -++=，2Y(s)3H(s)=X(s)(2)6s k =-++。

（2）当2k =-时，极点在虚轴上，为临界稳定系统；当2k <-，极点在左半平面，为稳定系统。

2．如图7-2所示系统中，已知且（1）求子系统H 2（s）；（2）欲使子系统H 2（s）为稳定系统，试确定k 的取值范围。

图7-2答：（1）如图221()()()()[()()()]()Y s E s Y s H s k E s Y s H s H s =+-+12121()()21()()()kH s H s H s kH s H s -==-+整理得，121()13()2[1()]2(3)kH s s K H s kH s s K +++==-+-（2）极点为k－3，当k－3＜0时，系统稳定，即，K＜3。