材料力学应力状态
- 格式:doc
- 大小:110.50 KB
- 文档页数:7


材料力学应力状态关键词:单元体的取法,莫尔应力圆的前提有那么一个单元体后(单元体其中的一对截面上主应力=0(平面)或平衡(空间),也就是单元体的一对截面为主平面),才有这么一个隔离体,才有那么一个莫尔应力圆和表达式也就是:取的单元体不同,则单元体的应力特点不一样,从而用截面法求任意截面上的应力取隔离体列平衡方程时,隔离体的受力特点不同,从而球出来的表达式也不同,只有这种表达式才适合莫尔应力圆。
因此拿到一个单元体后,不要急着应用莫尔应力圆,要先看它的特点适合不适合莫尔应力圆,也就是σα和τα的表达式球出来以后还是不是下面的这个公式。
特别还要记住,这个公式里的夹角α是斜截面的外法线与σx作用平σy的形式。
比如,面的外法线之间的夹角,这样公式中才是σx—当α表示的是斜截面的外法线与σ1所在平面的夹角,那么公式就是σ1—σ2的形式;不论是谁减谁,应力圆的性状都不变;1.首先,先有主平面和主应力的概念,剪应力为0的平面为主平面,主平面上的正应力为主应力;2.然后,由于构件受力情况的不同,各点的应力状态也不一样,可以按三个主应力中有几个不等于零而将一点处的应力状态划分为三类:∙单向应力状态:只有一个主应力不等于零,如受轴向拉伸和压缩的直杆及纯弯曲的直杆内各点的应力状态。
∙二向应力状态(平面应力状态):有两个主应力不等于零,如受扭的圆轴,低压容器器壁各点的应力状态。
∙三向应力状态:三个主应力都不等于零,如高压容器器壁内各点的应力状态。
3.然后,根据受力宏观判断是单轴应力状态还是平面应力状态还是三轴应力状态,取单元体关键,单元体取的不同,单元体上的应力也不同,做莫尔圆的繁简程度也不同,对于平面应力状态,当然要用主应力=0的那个截面参与单元体截取;4.单轴应力状态、平面应力状态、三轴应力状态是由主应力等于零的个数决定的,不受单元体取法的影响,也不是看单元体的三对截面上是否都存在正应力;比如单轴应力状态下,也可以取出一个单元体,让这个单元体的各平面上都有正应力和切应力,但是它仍然是单轴应力状态;同样,平面应力状态下,也可以取出一个单元体,让其各平面上都有正应力和剪应力,但它仍然是平面应力状态;5.按不同方位截取的单元体,尽管作用在这些单元体上的应力不同,但是在它们之间却存在着一定的关系:因为二者表示的是同一点的应力状态,因而可以从一个单元体上的应力求出另一个与其方向不同的单元体上的应力。

材料力学应力状态分析材料力学是研究物质内部力学性质和行为的学科,其中应力状态分析是材料力学中的重要内容之一。
应力状态分析是指对材料内部受力情况进行分析和研究,以揭示材料在外力作用下的应力分布规律和应力状态特征,为工程设计和材料选用提供依据。
本文将从应力状态的基本概念、分类和分析方法等方面展开讨论。
首先,我们来介绍一下应力状态的基本概念。
应力是指单位面积上的力,是描述物体内部受力情况的物理量。
在材料力学中,通常将应力分为正应力和剪应力两种基本类型。
正应力是指垂直于截面的应力,而剪应力是指平行于截面的应力。
在实际工程中,材料往往同时受到多种应力的作用,因此需要对应力状态进行综合分析。
其次,我们将对应力状态进行分类。
根据应力的作用方向和大小,可以将应力状态分为拉应力状态、压应力状态和剪应力状态三种基本类型。
拉应力状态是指材料内部受到拉力作用的状态,压应力状态是指材料内部受到压力作用的状态,而剪应力状态是指材料内部受到剪切力作用的状态。
这三种应力状态在工程实践中都具有重要的意义,需要我们进行深入的分析和研究。
接下来,我们将介绍应力状态分析的方法。
应力状态分析的方法有很多种,常用的有应力分析法、应变分析法和能量方法等。
应力分析法是通过应力分布的计算和分析来揭示应力状态的特征,应变分析法则是通过应变分布的计算和分析来揭示应力状态的特征,而能量方法则是通过能量原理和平衡条件来揭示应力状态的特征。
这些方法各有特点,可以根据具体情况选择合适的方法进行分析。
最后,我们需要注意的是,在进行应力状态分析时,需要考虑材料的本构关系、边界条件和载荷情况等因素,以确保分析结果的准确性和可靠性。
同时,还需要注意应力状态分析的结果对工程实践的指导意义,以便更好地指导工程设计和材料选用。
总之,材料力学应力状态分析是一个复杂而重要的课题,需要我们进行深入的研究和分析。
只有深入理解应力状态的特征和规律,才能更好地指导工程实践,为实际工程问题的解决提供科学依据。






材料力学应力状态
关键词:单元体的取法,莫尔应力圆的前提
有那么一个单元体后(单元体其中的一对截面上主应力=0(平面)或平衡(空间),也就是单元体的一对截面为主平面),才有这么
一个隔离体,才有那么一个莫尔应力圆和表达式
也就是:取的单元体不同,则单元体的应力特点不一样,从而用截面法求任意截面上的应力取隔离体列平衡方程时,隔离体的受力特点不同,从而球出来的表达式也不同,只有这种表达式才适合
莫尔应力圆。
因此拿到一个单元体后,不要急着应用莫尔应力圆,要先看它的特点适合不适合莫尔应力圆,也就是σα和τα的表达式球出来以后还是
不是下面的这个公式。
特别还要记住,这个公式里的夹角α是斜截面的外法线与σx
作用平
σy的形式。
比如,面的外法线之间的夹角,这样公式中才是σx—
当α表示的是斜截面的外法线与σ1所在平面的夹角,那么公式就是σ1—σ2的形式;不论是谁减谁,应力圆的性状都不变;
1.首先,先有主平面和主应力的概念,剪应力为0的平面为主平面,主平面上的正应力为主应力;
2.然后,由于构件受力情况的不同,各点的应力状态也不一样,可以按三个主应力中有几个不等于零而将一点处的应力状态划分为三类:
∙单向应力状态:只有一个主应力不等于零,如受轴向拉伸和压缩的直杆及纯弯曲的直杆内各点的应力状态。
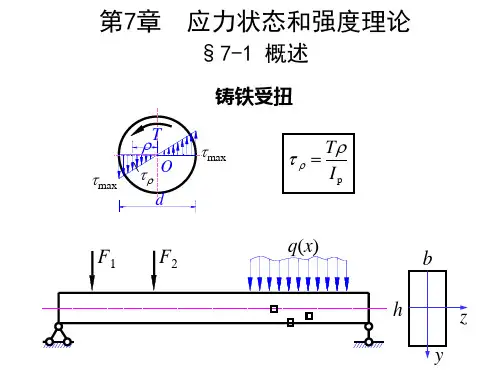
∙二向应力状态(平面应力状态):有两个主应力不等于零,如受扭的圆轴,低压容器器壁各点的应力状态。
∙三向应力状态:三个主应力都不等于零,如高压容器器壁内各点的应力状态。
3.然后,根据受力宏观判断是单轴应力状态还是平面应力状态还是三轴应力状态,取单元体关键,单元体取的不同,单元体上的应力也不同,做莫尔圆的繁简程度也不同,对于平面应力状态,当然要用主应力=0的那个截面参与单元体截取;
4.单轴应力状态、平面应力状态、三轴应力状态是由主应力等于零的个数决定的,不受单元体取法的影响,也不是看单元体的三对截面上是否都存在正应力;比如单轴应力状态下,也可以取出一个单元体,让这个单元体的各平面上都有正应力和切应力,但是它仍然是单轴应力状态;同样,平面应力状态下,也可以取出一个单元体,让其各平面上都有正应力和剪应力,但它仍然是平面应力状态;
5.按不同方位截取的单元体,尽管作用在这些单元体上的应力不同,但是在它们之间却存在着一定的关系:因为二者表示的是同一点的应力状态,因而可以从一个单元体上的应力求出另一个与其方向不同的单元体上的应力。
6.既然怎么取单元体不影响一点的应力状态:无论你怎么取,应力状态就在那里,不会发生变化,那么就可以取主平面所确定的单元体或者有主平面参与的单元体,研究起来方便点,可以用莫尔应力圆来研究。
不管怎么取单元体,只要知道了它各个面上的应力,那么总可以作出莫尔圆:
(即:依次作出单元体与三对平面分别垂直的这些截面的应力圆;那么就有三个应力圆;三个应
力圆包起来就是任意截面的;
特别注意:一点出的截面有无数个,全方位都有,一般是先做与单元体各个截面垂直的那三组截面;----------括号内的说法是错误的,因为先做与单元体的三个截面分别垂直的这三组截面的应力圆的前提是,单元体的三个平面是主平面,其上只有主应力,这样才能使得取出的隔离体上在一个方向上是只有正应力(某一个主应力),这对正应力平衡,从而简化成了平面应力状态的莫尔圆;因此若取出的单元体是那种三对截面上既有正应力又有剪应力的,便不能用这种简单的方法了,那时将会很复杂,就是另外的隔离体和受力状态了,重新列平衡方程,得到新的表达式;就不是莫尔应力圆的圆的方程的表达式了。
7
表面的一点A截取单元体时,把所用的一对横截面和一对径向纵截面,改成一对与轴
线成45°和一对与轴线成135°的斜截面来代替(下图中的a),那么截出的单元体及
其上面所作用的应力将变成如图c所示的那样,它完全改变了原来所截取的单元体上
的应力情况(图b所示的)。
应当指出,按不同方位截取的单元体,尽管作用在这些单
元体上的应力不同,但是在它们之间却存在着一定的关系:因为二者表示的是同一点
的应力状态,因而可以从一个单元体上的应力求出另一个与其方向不同的单元体上的
应力。
一般情况下,在单元体的三对相互垂直的平面上既作用有正应力,也作用有剪应力。
如果在单元体的各个平面上只作用有正应力,而没有剪应力,则称这样的平面为主平面,称作用在主平面上的正应力为主应力。
由于主平面上没有剪应力,用由三对主平面构成的单元体来表示一点的应力状态便于对各种受力构件的应力状态进行比较。
所以,在表示-点的应力状态时,就不任意截取单元体了,而是截取由三个主平面构成的单元体,即一点的应力状态用该点的三个主应力来表示(如上右图)。
三个主应力分别用σ1、σ2和σ3来表示,它们是按代数值大小的顺序排列的,即σ1>σ2>σ3>,其中σ可为负值,也可等于零。
如上左图c所示的三个主应力σ1是拉应力,σ2是零,σ3是压应力。