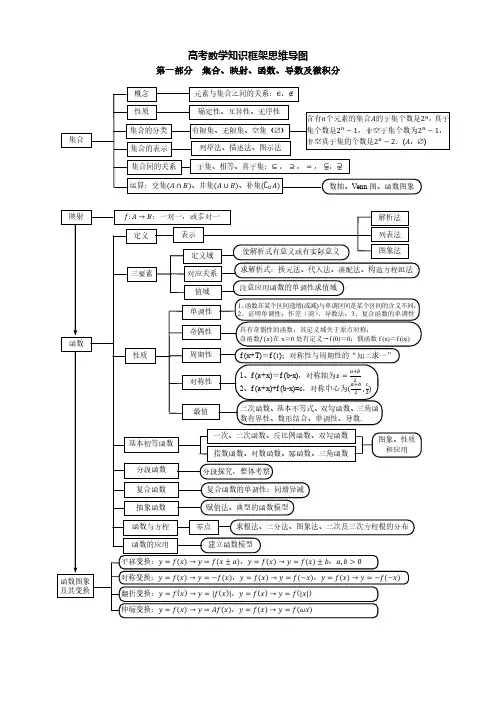
【思维导图】一元函数微分学-

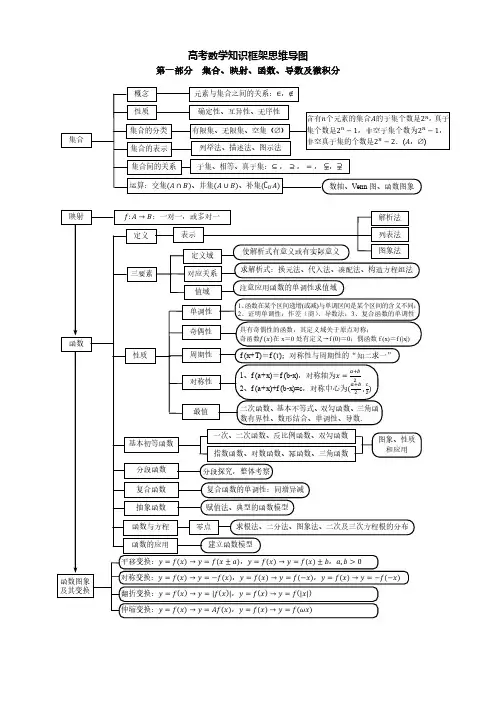
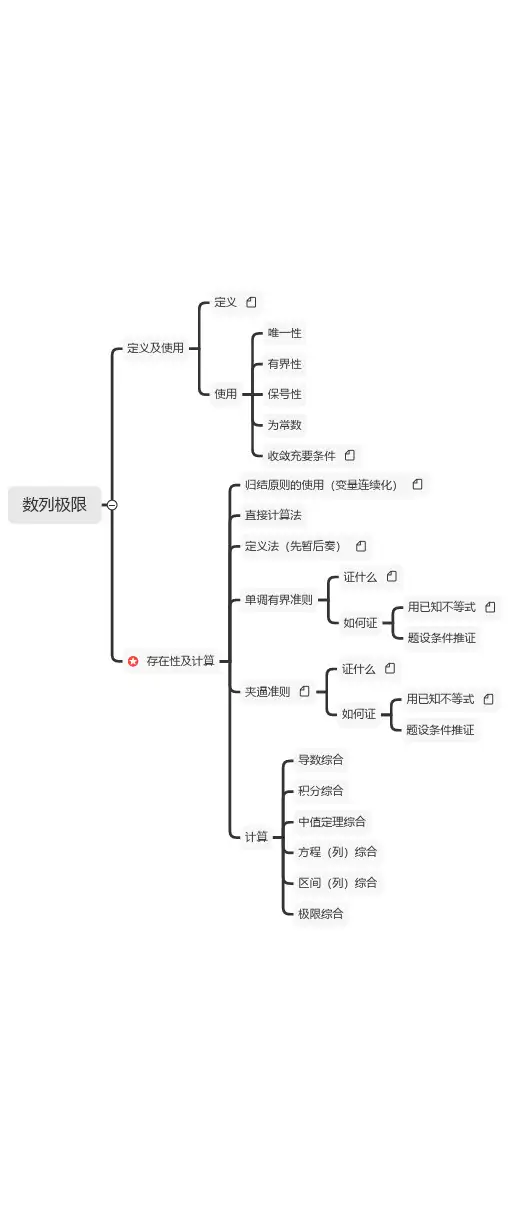
第二章 一元函数微分学一．与导数的定义有关的考点 先回顾导数的定义： 设函数()x f y =在()x U内有定义，如果极限()()x x x f x f x x 000lim--→存在，则称()x f y =在x 0处可导，x 0称为函数()x f 的可导点，且称上述极限值为函数()x f 在x 0处的导数，记为：|0x dx dy x =或|0x dx dfx =；或简记为()x f 0'． 注意导数的本质是瞬时变化率，它还有另外两种常见的等价定义： 1．()x f 0'=()()xf x f x x x ∆-∆+→∆000lim；2．()()()00lim.x fh f f x hx xx →+-'=；要特别关注0x =处的导数有特殊形式：()()()00lim.x f x f f x→-'=（更特别地，()()()()()000lim.00x f x f f f x→-'==如。

要知道两个重要的结论：1.可导必连续；2。

函数()x f y =在x 0处可导的充要条件是()()//00.f x f x -+=对于分段函数在分段点处的可导性，一定从要考察其左、右导出发.例1．已知()x f 0'=A ，试求下列极限的值 （1）()());(lim000A xf x f x x x -=∆-∆-→∆（2）。

()());4(3lim000A xx f x f x x x =∆∆--∆+→∆例2．研究函数()||x x f =在0=x 处的可导性. 解：因为()()()/000lim lim 1000x x f x f x f x x---→→---===-- 同理，可求得()10/=+f .由于()()00//f f +-≠，所以()||x x f =在0=x 处不可导。

（记住这个结论）练习：设()()2,0,1,0.axe xf x b x x ⎧≤⎪=⎨->⎪⎩在0x =处可导，求,a b 的值. 解：（一）因为()f x 在0x =处可导，从而()f x 在0x =处也连续.所以，()()0lim lim ,x x f x f x -+→→=即 1.b = （二）()()()/00010limlim ;0ax x x f x f e fa x x---→→--===- ()()()()22/001120limlim lim 2.0x x x f x f x x xfx xx+--+→→→----====-- 由()()//00f f -+=，得2a =-.例3． 已知()x x f 2=，试求()x f 在2=x 处的导数.解：因为2224lim lim(2)42x x x x x →→-=+=-，所以，()2 4.f '=由此例可见，在导数存在的情况下，求导问题就归结为求一个0型的极限.故求导就是求极限，不必多举例，今后很少针对具体函数计算在一点处的导数值. 如把函数在一点x 0处可导的概念推广到一个区间，则可得到导函数的概念.大家要牢记基本导数表（共十五、六条）。

§3 一元函数微积分3.1 微分一元函数可记为)(x y y = 或 )(x F y =在它的连续区域内，如图附-20所示，自变量若从x 增加到x x ∆+，便称x ∆为自变量x 的增量。

相应地，自变量从)(x y 增加到)(x x y ∆+，称)()(x y x x y y -∆+=∆为函数增量。

y x ∆∆、既可以是正的，也可以是负的。

几个函数的y x ∆∆、间关系如下：B Ax y += []x A B Ax B x x A y ∆=+-+∆+=∆)()( 2Ax y = 222)(2)(x A x Ax Ax x x A y ∆+∆=-∆+=∆x y sin = x x x x x x x y ∆+-∆=-∆+=∆sin cos )1(cos sin sin )sin( x e y = )1(-=-=∆∆∆+x x x x x e e e e y 例中B A ,均是常量。

自变量增量0→∆x 时，称为自变量微分，改记成dx 。

dx 是无穷小量，但不是零。

在连续区域内，自变量增量取微分dx 时，函数增量0→∆y ，称为函数微分，记成dy ，它也是无穷小量，可正，可负。

dy 与dx 间关系为)()(x y dx x y dy -+= 几个实例如下：B Ax y += Adx dy =2Ax y = dx dx x A dy )2(+=x y s i n= dx x dx x dy sin cos )1(cos sin +-= xe y = )1(-=dxxee dy数学中可以证明，对无穷小量dx ，有Ax Bdx Ax →+ 简书为 Ax Bdx Ax =+ 1cos →dx 简书为 1cos =dx dx dx →sin 简书为 dx dx =sin dx dx →tan 简书为 dx dx =tan e dx dx→+1)1( 简书为 ...718281828.2)1(1==+e dx dx例题6. 试证 dx dx dx ==tan sin 。

高一数学函数思想导图总结高一数学函数思想导图总结一、函数的基本概念1. 函数的定义：函数是一种特殊的关系，它把一个数集的每个元素都对应到另一个数集的唯一元素。

2. 自变量与因变量：自变量是已知的数值，在函数中起到输入的作用；因变量是待求的数值，在函数中起到输出的作用。

3. 函数的图像：函数的图像是自变量和因变量之间的对应关系在平面上的表示，可通过给定的函数表达式绘制出来。

二、函数的性质1. 定义域和值域：定义域是自变量的取值范围，值域是因变量的取值范围。

2. 奇偶性：奇函数满足 f(-x) = -f(x)，偶函数满足 f(-x) = f(x)，可以通过函数的图像来判断其奇偶性。

3. 单调性：函数的单调性描述了函数图像上的任意两点之间的高低变化趋势，可以通过函数的导数来判断。

4. 周期性：周期函数满足 f(x+T) = f(x)，其中 T 为正数，函数的图像在一定区间内重复出现。

三、基本函数1. 常数函数：f(x) = c，其中 c 为常数，函数图像平行于 x 轴。

2. 一次函数：f(x) = kx + b，其中 k 和 b 均为常数，函数图像是一条直线。

3. 二次函数：f(x) = ax^2 + bx + c，其中 a、b 和 c 为常数，函数图像是抛物线。

4. 绝对值函数：f(x) = |x|，函数图像在原点处有拐点。

5. 幂函数：f(x) = x^n，其中 n 为整数，函数图像的形状与 n的正负相关。

6. 指数函数：f(x) = a^x，其中 a 为正常数且不等于 1，函数图像在点 (0, 1) 处经过。

四、复合函数1. 复合函数的定义：将两个或多个函数相互结合，得到一个新函数，新函数的自变量是原函数的因变量。

2. 复合函数的运算：复合函数的运算按照从内到外的顺序进行，即先求内函数值再求外函数值。

3. 复合函数的性质：复合函数的定义域由内外函数的定义域决定，复合函数的周期取内外函数周期的最小公倍数。