流体静力平衡方程

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

行星流体静力平衡-概述说明以及解释1.引言1.1 概述在宇宙中，行星是一个独特且神秘的存在。

它们由各种不同的物质组成，拥有独特的形态和性质。

在行星内部，存在着大量的流体，包括液态和气态物质，这些流体在行星内部通过各种力学过程相互作用。

本文将探讨行星内部流体的静力平衡条件，揭示行星结构和演化的一些奥秘。

通过深入研究行星内部的流体力学基础和流体静力平衡条件，我们可以更好地理解行星的形成和演化过程，为人类认识宇宙和地球提供更深层次的认识。

1.2 文章结构本文主要分为引言、正文和结论三个部分。

在引言部分，将对行星流体静力平衡的概念进行概述，介绍文章的结构和目的，为读者提供了解本文内容的指引。

在正文部分，将首先介绍流体力学基础知识，包括流体静力学的基本概念和原理。

然后将探讨行星内部结构的特点，揭示行星内部流体的分布和运动规律。

最后，重点讨论流体静力平衡条件在行星内部的作用和影响。

在结论部分，将对本文的主要内容进行总结，探讨流体静力平衡条件在实际应用中的意义和展望未来的研究方向。

最后，简要总结全文，为读者留下深刻印象。

1.3 目的本文的目的是探讨行星内部的流体静力平衡条件，通过深入研究流体力学基础和行星内部结构，分析行星内部的力学平衡状态。

通过本文的研究，我们希望能够更深入理解行星的形成和演化过程，为地球科学领域提供新的视角和理论支持。

同时，通过对行星内部的流体静力平衡条件的探讨，可以为未来行星探测和地质研究提供一定的参考依据，推动相关领域的发展和进步。

2.正文2.1 流体力学基础流体力学是研究流体运动及其力学性质的学科，是物理学中的一个重要分支。

流体是指没有固定形状且可以流动的物质，例如水、空气等。

在流体力学中，我们通常使用一些重要的概念和理论来描述流体的运动和性质。

首先，我们需要了解流体的性质。

流体具有体积的连续性和不可压缩性。

体积的连续性原理表明，在没有外力作用的情况下，流体的体积始终保持不变。

而不可压缩性则意味着流体的密度在运动中保持不变。

静力学方程和伯努利方程静力学方程和伯努利方程是流体力学中两个重要的方程，它们在解决各种流体力学问题中起到关键的作用。

本篇文章将对这两个方程进行全面的介绍和解释，并指导读者如何应用它们解决实际问题。

静力学方程是描述静止流体的力学行为的基本方程之一。

它由两个部分组成，即压力方程和液体静力平衡方程。

压力方程是指在静止的流体中，压力随深度增加而增加的原理。

我们知道，液体会受到重力的作用，所以液体的底部压力要高于顶部的压力。

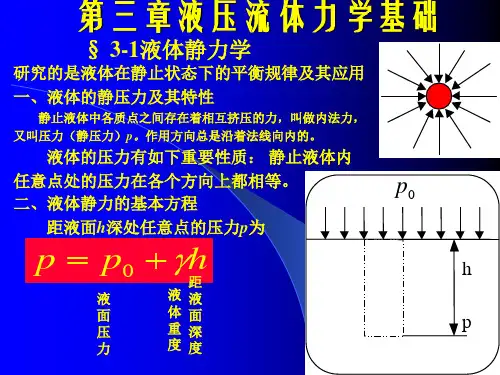
液体的压力可以用公式P = ρgh表示，其中P表示液体某一深度处的压力，ρ表示液体的密度，g表示重力加速度，h表示液体的深度。

这个公式告诉我们，液体的压力是与液体的深度和密度有关的。

液体静力平衡方程描述了在静止的流体中，压力的分布情况。

根据这个方程，当液体处于静止状态时，液体内部各点的压力相等。

这个方程在求解许多与静止流体有关的问题时非常有用，比如确定液体的压力、液体对固体的支撑力等。

伯努利方程是描述流体在不同位置间能量转换和流速变化的理论基础。

它是通过对流体的能量守恒和质量守恒进行推导得到的。

伯努利方程可以用于解决许多与流体力学有关的实际问题，比如水管流速与压力的关系、飞机飞行的升力产生机制等。

伯努利方程是由下面的公式表示的：P + 1/2ρv^2 + ρgh = 常数其中P表示液体的压力，ρ表示液体的密度，v表示液体的流速，g表示重力加速度，h表示液体的高度。

这个方程告诉我们，在流体运动过程中，流体的压力、速度和高度之间存在着一种关系，即当流体速度增加时，压力会降低，而当流体速度降低时，压力会增加。

通过静力学方程和伯努利方程，我们可以解决很多与流体力学有关的实际问题。

比如，当我们需要计算液体的压力、流速、流量等时，可以利用这两个方程来求解。

此外，在设计和优化各种流体系统时，也可以应用这两个方程来指导工程实践。

总之，静力学方程和伯努利方程是流体力学中两个重要的方程。

它们不仅能够解释流体的基本力学行为，还能够指导我们解决与流体有关的实际问题。

流体静力学方程的适用条件(一)流体静力学方程的适用条件引言流体静力学是研究流体在静力平衡状态下的行为规律的学科，描述了流体静力学方程的适用条件对于理解和解决流体的静态问题非常重要。

适用条件在研究流体静力学方程的适用条件时，需要考虑以下几个方面：1.静态平衡条件–流体必须处于静力平衡状态，即没有加速度和剪切力的存在。

–流体内部各点之间的压强相等，即存在等压面。

这要求流体没有外力或外压作用。

2.宏观尺度–流体静力学方程适用于宏观尺度，即适用于大尺度上对流体进行整体平均的情况。

–该方程不适用于涉及微观尺度或有明显界面效应的情况。

3.不可压缩性–流体静力学方程假设流体是不可压缩的，即流体密度在空间和时间上保持不变。

–在某些特殊情况下，对于可压缩流体，可以通过适当的近似方法将其视为不可压缩流体进行处理。

4.没有动力学效应–流体静力学方程适用于没有动力学效应的情况，即流体中没有涡旋运动或渗透流存在。

总结流体静力学方程的适用条件主要包括静态平衡、宏观尺度、不可压缩性和没有动力学效应等。

在理解和应用流体静力学方程时，我们必须考虑这些条件，并根据具体情况进行适当的近似和简化。

这些适用条件是我们研究和解决流体静态问题的基础。

以上是针对流体静力学方程的适用条件的相关介绍，希望能对读者有所帮助。

应用范围流体静力学方程的适用条件在很多领域都有广泛的应用，包括但不限于以下几个方面：1.工程液压学–在液压系统中，通过流体静力学方程可以计算液压系统中的压力分布、液体高度等参数。

–这有助于优化液压系统的设计和运行，提高系统的效率和安全性。

2.建筑水力学–在水资源工程中，流体静力学方程可用于计算大坝、堤坝和水闸等结构的承压能力。

–这可以帮助工程师评估工程结构的稳定性，并制定相应的安全措施。

3.管道输送–在管道系统中，流体静力学方程可用于计算流体在管道中的流速和压力分布。

–这对于优化管道输送系统的设计和运行非常重要，能够提高流体的输送效率和节约能源。

静力学平衡方程静力学平衡方程静力学平衡方程是物理学中一个重要的概念，是力学中用于描述物体所受外力作用下的静止状态的基本定理。

在数学上，这个方程被表达为：ΣF = 0其中ΣF表示作用在物体上的所有力的矢量和，等于零表示物体处于静止状态。

这个方程包含了牛顿第一定律，即一个物体如果受到的合力为零，则其将保持静止或匀速直线运动。

在工程学和物理学中，这个方程被广泛应用于杠杆、支撑结构、桥梁等工程中。

工程师通过运用这个方程来计算物体能否保持平衡，以及所需要的支撑结构大小和材料强度等参数。

杠杆原理杠杆原理是静力学平衡方程中应用最为广泛的应用之一，特别是在机械和结构工程中。

杠杆按位置分为一类，二类和三类。

在一类杠杆中，力和支点的位置关系导致了杠杆的刚性比较小，所以在外力相等的情况下，较小力的杆杆就可以产生比较大的力矩，从而达到平衡的效果。

例如，一个人试图从一个杆子上旋起一个沉重的箱子。

这个箱子对于人来说可能是太重了，但当他用一个搬运杆来支撑这个箱子时，他只需要用比箱子重的更小的力来旋转搬运杆，从而达到平衡的效果。

支撑结构另一个重要的应用是支撑结构。

在物理学和工程学中，支撑结构是指支撑物体并通过承受一定负载来保持稳定平衡的任何物体。

举个例子，一个高楼需要一定的支撑结构来承受地心引力以及风力等对建筑的作用力。

支撑结构必须满足静力学平衡方程，使支撑物体的重力和其他作用力等于零。

通过分析材料的强度和平衡方程，工程师可以计算出所需的支撑结构大小和材料强度，从而设计出完美的支撑结构。

桥梁桥梁结构也需要应用静力学平衡方程来保持稳定。

桥梁通常是由高低不平的地面或水体中跨过而设计的。

在设计桥梁时，需要考虑桥梁的重量、材料强度和内部支撑结构，以确保桥梁稳定平衡。

在桥梁支撑结构的设计中，静力学平衡方程是一个重要的工具。

通过计算桥墩、悬挂和支撑结构对于承受负载所产生的力和力矩，工程师可以确定支撑结构的安全度，从而设计桥梁的内部结构。

总结在物理学和工程学中，静力学平衡方程是至关重要的一个概念。

工程流体力学中的液体受力分析工程流体力学是研究流体在各种工程系统中的力学行为的学科。

液体是流体力学研究的主要对象之一，液体受力分析是工程流体力学中的重要内容。

液体受力分析通过研究液体的受力机制，可以帮助我们理解液体在不同工程系统中的行为，并为工程设计提供依据。

本文将深入探讨液体受力分析的相关内容。

首先，液体受力分析的基础是流体静力学。

在静力学中，我们研究不可压缩流体在静止状态下的力学行为。

液体受力分析的首要任务是确定液体所受的压力力和重力力。

液体受力分析通常涉及到用到的两个基本公式：静力平衡方程和亥姆霍兹自由能方程。

静力平衡方程描述了液体处于平衡状态时各个位置的受力平衡条件。

根据静力平衡方程，液体内部的压力在各个方向上都是均匀的，且沿任意曲线方向的压力的变化率与液体的密度以及加速度大小成正比。

这个方程对于液体的受力分析起到了重要的作用。

亥姆霍兹自由能方程是对液体受力分析的另一个重要工具。

亥姆霍兹自由能方程描述了液体在稳态条件下的能量守恒规律。

根据亥姆霍兹自由能方程，液体的总能量等于机械能、热能和化学能之和。

液体受力分析需要通过这个方程来分析液体在不同工程系统中的能量变化和能量转换过程。

液体受力分析在很多工程应用中都有广泛的应用。

例如，在水坝工程中，液体受力分析可以帮助工程师确定水坝的稳定性和抗风浪能力，为水坝的设计提供科学依据。

又如，在管道系统设计中，液体受力分析可以帮助工程师确定管道中液体的流动速度和压力分布，提高管道系统的运行效率和安全性。

液体受力分析还可以应用于水力发电站、河流和海洋结构工程、水泵和风扇系统等领域。

在这些工程中，液体受力分析可以帮助工程师确定液体的流动特性、阻力、压力分布和能量损失等，从而优化系统设计。

总而言之，液体受力分析是工程流体力学中的重要内容，通过研究液体的受力机制，可以帮助我们理解液体在不同工程系统中的行为，并为工程设计提供依据。

液体受力分析的基础是流体静力学，主要包括静力平衡方程和亥姆霍兹自由能方程。