当前位置：文档之家 › 圆周角定理课件(PPT 17页)

圆周角定理课件(PPT 17页)

  • 格式：ppt
  • 大小：453.00 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

数学九年级上第三篇第四节《圆周角》课件

数学九年级上第三篇第四节《圆周角》课件
数学九年级上第三篇第四节《圆周 角》课件
目录
• 圆周角基本概念与性质 • 圆周角定理及其推论 • 弧长与扇形面积计算 • 圆锥曲线中圆周角应用 • 拓展延伸：其他几何图形中圆周角应用 • 总结回顾与课堂练习
01 圆周角基本概念与性质
圆周角定义及特点
圆周角定义
顶点在圆上，并且两边都和圆相 交的角叫做圆周角。
圆周角性质总结
01
02
03
性质1
在同圆或等圆中，如果两 个圆周角相等，那么它们 所对的弧也相等。
性质2
在同圆或等圆中，如果两 条弧相等，那么它们所对 的圆周角也相等。
性质3
在同圆或等圆中，同弧或 等弧所对的圆周角相等， 都等于这条弧所对的圆心 角的一半。
02 圆周角定理及其推论
圆周角定理内容
ห้องสมุดไป่ตู้圆周角定义
圆柱、圆锥等立体图形中圆周角应用
圆柱中的圆周角
圆柱侧面展开图是一个矩形，其相邻两边夹角即为圆周角。利用圆周角定理可解决圆柱中 的相关问题。
圆锥中的圆周角
圆锥侧面展开图是一个扇形，其圆心角即为圆锥的顶角，而圆周角则为顶角的一半。利用 这些性质可解决圆锥中的相关问题。
圆周角定理在立体图形中的应用
在解决立体图形的问题时，可利用圆周角定理将问题转化为平面问题，从而简化计算过程 。
设扇形半径为r cm，则根据扇 形面积计算公式有 (45° × π × r²) / 360 = 24cm²，解得 r≈4.37cm（保留两位小数）。 再根据弧长计算公式，弧长 = 45° × 4.37cm × π / 180 ≈ 3.43cm（保留两位小数）。
04 圆锥曲线中圆周角应用
圆锥曲线基本概念回顾
典型例题解析

圆周角定理 课件

圆周角定理 课件
圆周角定理
1.圆周角定理
文字
语言
圆上一条弧所对的圆周角等于它所对的圆心角的一半
图形
语言
符号
在☉O 中, BC 所对的圆周角和圆心角分别是∠BAC,∠
1
语言
BOC,则有∠BAC= ∠BOC
作用
确定圆中两个角的大小关系
2
名师点拨定理中的圆心角与圆周角一定是对着同一条弧,它们才
有上面定理中所说的数量关系.
证明:∵BC是☉O的直径,DA∽Rt△BAC.
∴∠BAD=∠ACB.
∵ = , ∴∠FBA=∠ACB,
∴∠BAD=∠FBA.
∴△ABE为等腰三角形.
∴AE=BE.
反思1.有关圆的题目中,圆周角与它所对的弧经常相互转化,即欲
证明圆周角相等,可转化为证明它们所对的弧相等;要证明线段相
∴ 所对圆心角是360°-150°=210°,
1
2
∴ 所对圆周角∠BCD= × 210°= 105°.
答案:105°
反思同弦或等弦所对的圆周角不一定相等.当弦是直径时,同弦或
等弦所对的圆周角相等,都等于90°;当弦不是直径时,该弦将圆周分
成两条弧:优弧和劣弧,若圆周角的顶点同在优弧上或同在劣弧上,
作用
确定圆弧或圆心角的度数
【做一做 2】 如图,两个同心圆中, 的度数是 30°,
且大圆的半径 = 4, 小圆的半径 = 2, 则 的度数是________.
解析: 的度数等于∠AOB,又 的度数也等于∠AOB,则
的度数是30°.
答案:30°
3.圆周角定理的推论
【做一做1】 如图,在☉O中,若∠BAC=25°,则∠BOC等于(
A.25°

圆周角定理 课件

圆周角定理 课件

如图 2－1－2，△ABC 的角平分线 AD 的延长 线交它的外接圆于点 E.
图 2－1－2 (1)证明：△ABE∽△ADC； (2)若△ABC 的面积 S＝12AD·AE，求∠BAC 的大小．
【思路探究】 (1)通过证明角相等来证明三角形相似． (2)利用(1)的结论及面积相等求 sin∠BAC 的大小，从而 求∠BAC 的大小． 【自主解答】 (1)由已知条件，可得∠BAE＝∠CAD. 因为∠AEB 与∠ACB 是同弧上的圆周角，所以∠AEB＝ ∠ACD. 故△ABE∽△ADC.
(2)因为△ABE∽△ADC，所以AABE＝AADC，即 AB·AC＝ AD·AE.
又 S＝12AB·ACsin∠BAC 且 S＝12AD·AE， 故 AB·ACsin∠BAC＝AD·AE， 则 sin∠BAC＝1，又∠BAC 为三角形内角，所以∠BAC ＝90°.
1．解答本题(2)时关键是利用 AB·AC＝AD·AE 以及面积 S ＝12AB·ACsin∠BAC 确定 sin∠BAC 的值．
圆周角定理
1．圆周角定理及其推论 (1)圆周角定理：圆上一条弧所对的 圆周角 等于它所 对的 圆心角 的一半． (2) 推 论 1 ： 同弧或等弧 所 对 的 圆 周 角 相 等 ； 同圆或等圆 中，相等的圆周角所对的 弧 也相等． (3)推论 2： 半圆 (或 直径 )所对的圆周角是直角；90° 的圆周角所对的弦是 直径 ．
在圆中，直径是一条特殊的弦，其所对的圆周角是直角， 所对的弧是半圆，利用此性质既可以计算角大小、线段长度 又可以证明线线垂直、平行等位置关系，还可以证明比例式 相等．
如图 2－1－5，已知等腰三角形 ABC 中，以腰 AC 为直
径作半圆交 AB 于点 E，交 BC 于点 F，若∠BAC＝50°，则

圆周角定理 课件

圆周角定理 课件
先由三角形相似得线段成比例,再求其长度.
解:(1)∵AE平分∠BAC,
∴∠BAD=∠EAC.
又∵∠B=∠E,∴△ABD∽△AEC.
∵∠B=∠E,∠BAE=∠BCE,
C,
∴

=CE2.=ED·
∴
AE,

∴16=2AE,∴AE=8.
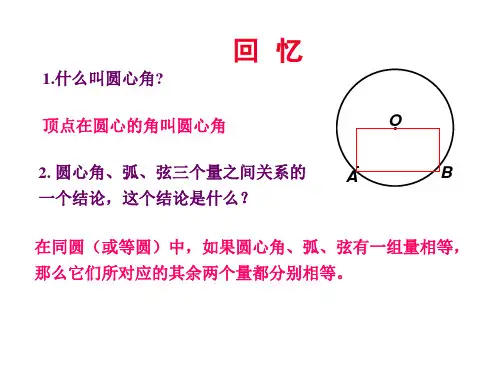
圆周角定理
题型一
求线段的长
【例1】 如图,△ABC的三个顶点都在☉O上,∠BAC的平分线与
BC边和☉O分别交于点D,E.
(1)指出图中相似的三角形,并说明理由;
(2)若EC=4,DE=2,求AD的长.
分析:(1)本题证明两个三角形相似,要用三角形相似的判定定理,
而其中角的条件由同弧所对的圆周角相等得出;(2)要求线段长度,
又∵AD⊥BC,∴Rt△BDA∽Rt△BAC.
∴∠BAD=∠ACB.
∵ = , ∴∠FBA=∠ACB,
∴∠BAD=∠FBA.
∴△ABE为等腰三角形.
∴AE=BE.
题型三
易错辨析
易错点:误认为同弦或等弦所对圆周角相等而致错
【例3】 如图,若∠BAD=75°,则∠BCD=
错解:∵∠BAD和∠BCD所对的弦都是BD,
∴AD=AE-DE=6.
反思求圆中线段长时,常先利用圆周角定理及其推论得到相似三
角形,从而得到成比例线段,再列方程求得线段长.
题型二
证明线段相等
【例 2】 如图,BC 为圆 O 的直径,AD⊥BC, =
, 和相交于. 求证: = .
证明:∵BC是☉O的直径,
∴∠BAC为直角.
上,同弦或等弦所对的圆周角相等;若一个圆周角的顶点在优弧上,
另一个圆周角的顶点在劣弧上,则同弦或等弦所对的圆周角不相等,

《圆周角》课件精品 (公开课)2022年数学PPT全

《圆周角》课件精品 (公开课)2022年数学PPT全
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解圆周角的概念，会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理解 决简单的几何问题.（重点、难点） 3.理解掌握圆周角定理的推论及其证明过程和运用. （难点）
导入新课
复习引入
（5）√
A B
（6）√
二 圆周角定理及其推论
测量与猜测
如图，连接BO,CO,得圆心角∠BOC.试猜想∠BAC与 ∠BOC存在怎样的数量关系.
BAC1BOC 2
推导与论证
圆心O在∠BAC 的一边上
圆心O 在∠BAC
的 内部
圆心O在∠BAC 的外部
n圆心O在∠BAC的一边上（特殊情形）
OA=OC ∠A= ∠C ∠BOC= ∠ A+ ∠C
证明猜想
∵ 弧BCD和弧BAD所对的圆心角的和是周角， ∴∠A＋∠C＝180°， 同理∠B＋∠D＝180°，
归纳总结
推论：圆的内接四边形的对角互补.
想一想
图中∠A与∠DCE的大小有何关系？
∵ 弧BCD和弧BAD所对的圆心角的和是周角，
∴∠A＋∠C＝180°，
D
同理∠B＋∠D＝180°， A
延长BC到点E，有
2∠BOC. 求证：∠ACB=2∠BAC.
证明： ACB1AOB,
2
1
BAC BOC,
O
2
∠AOB=2∠BOC，
A
C B
∴∠ACB=2∠BAC
9.船在航行过程中，船长通过测定角数来确定是否遇到
暗礁，如图，A、B表示灯塔，暗礁分布在经过A、B两

圆周角优秀课件

圆周角优秀课件
1.圆周角定义:顶点在圆上,并且两边都和圆相 交的角叫圆周角.
2.半圆或直径所对的圆周角等于90° 90°的圆周角所对的弦是直径
3.在同圆(或等圆)中，同弧或等弧所对的圆周角相 等,同弧或等弧所对的圆周角等于圆心角的一半；相 等的圆周角所对的弧相等。
在同圆或等圆中，如果两个圆周角相等， 它们所对弧一定相等吗？为什么？
2
∠BAD＋∠CAD＝ 1∠ BOD＋ 1∠COD
2
2
即∠BAC= 1 ∠BOC 2
3.第三种情况：
A
证明：作射线AO交⊙O于D。
由第1种情况得 ∠CAD＝ 1 ∠ COD
2
O C
DB
∠BAD＝
1 2
∠ BOD
∠CAD－∠BAD＝ ห้องสมุดไป่ตู้ ∠ COD－ 1 ∠BOD
2
2
即∠BAC= 1 ∠BOC 2
归纳总结
A
E B
C D
E
●O
C
A⌒C所对的圆周角∠ AEC ∠ ABC
∠ ADC的大小有什么关系？
B
规律：都相等，都等于圆心角∠AOC的一半
D
结论：同弧或等弧所对的圆周角相等。
练习:
1、如图，在⊙O中，ABC=50°，
则∠AOC等于（ D）
A、50°；
B、80°；
C、90°；
D、100°
A
BO C
2、如图，△ABC是等边三角形，动点P
圆周角定理
C
在同圆或等圆中，同弧(或等弧）所对 的圆周角相等；同弧(或等弧）所对的 圆周角等于圆心角的一半．
D A
O·
B E
推论
C2
C1
C3
直径（或半圆）所对的圆周角是 直角， 90°的圆周角所对的弦是 A

人教版数学九年级上册 第24章 圆 24.1.4 圆周角 课件(共16张PPT)优质课件PPT

人教版数学九年级上册 第24章 圆 24.1.4 圆周角 课件(共16张PPT)优质课件PPT
2.与圆周角有关的问题： 弦的条件需转化成弧 的条件。
•
我们很容易遭遇逆境，也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间，如果不前进，不会自我激励的话，就注定只能被这个世界抛弃。自我激励能力是人自我调节系
统中重要的组成部分，主要表现在对于在压力或者困境中，个体自我安慰、自我积极暗示、自我调节的能力，在个体克服困难、顶住压力、勇对挑战等情况下，都发挥着关键性的作用。具备
D
的圆周角”的数量关系，就转化为圆
内接四边形的对角之间的数量关系，
也就是本节课的主题。
探究性质
B
O
A
C
D
圆内接四边形ABCD的对角 有什么数量关系？
通过学生自己动手画图、测量、 猜想，最后证明结论，探究得出 圆内接四边形的性质
B
性质：
50
圆内接四边形的对角互补.
O
延伸：
A
130 50C D
圆内接四边形的任意一个 外角等于它的内对角.
自我激励能力的人，富有弹性，经常表现出反败为胜、后来居上、东山再起的倾向，而缺乏这种能力的人，在逆境中的表现就大打折扣，表现为过分依赖外界的鼓励和支持。一个小男孩在自
家的后院练习棒球。在挥动球棒前，对自己大喊：“我是世界上最棒的棒球手！”然后扔出棒球，挥动……但是没有击中。接着，他又对自己喊：“我是世界上最棒的棒球手！”扔出棒球，
难对于脑力运动者来说，不过是一场场艰辛的比赛。真正的运动者总是盼望比赛。如果把困难看作对自己的诅咒，就很难在生活中找到动力，如果学会了把握困难带来的机遇，你自然会动力
O A OB
C
C
AB 2.半圆(或直径)所
O
对的圆周角是直
O
角, 90的圆周角

课件3：一 圆周角定理

课件3：一 圆周角定理

再见
点评：当题目结论与比例式有关时,可考虑证明三角形相似．
3．在⊙O 内有一个内接四边形 ABCD，AC 与 BD 交于点 E， 求证：ABEE＝ABDC.
︵︵ 证明：由AB＝AB， 得∠ADE＝∠ACB. 又∠AED＝∠BEC，
∴△AED∽△BEC，即ABEE＝ABDC.
4．如图所示，已知⊙O中，∠AOB＝2∠BOC，求 证∠ACB＝2∠BAC. 分析：利用圆周角定理证明． 证明：∵∠ACB＝∠AOB， ∠AOB＝2∠BOC， ∴∠ACB＝∠BOC. 又∵∠BAC＝∠BOC， ∴∠ACB＝2∠BAC.
►变式BC＝4 cm,则OD ＝__2_c_m____． 2.如图所示,圆O上一点C在直径AB上的射影为D,CD＝4,BD＝8,圆 O的半径r＝___5_____．
题型二 证明问题
例2 已知AD是△ABC的高，AE是△ABC的外接圆的直径，求证： ∠BAE＝∠DAC. 分析：题目中出现圆的直径，想到直径所对的圆周角是直 角．因此，连接BE，得到∠ABE＝90°.同时，在△ABE与 △ADC中，又有同弧所对的圆周角∠C与∠E相等，从而结论 得以证明． 证明：如图，连接BE.
一 圆周角定理
圆周角定理 圆上一条弧所对的圆周角等于它所对的圆心角的一半.
圆心角定理
圆心角的度数等于它所对弧的度数. 推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所 对的弧也相等. 推论2
半圆（或直径）所对的圆周角是直角;900的圆周角所对的 弦是直径
题型一 角、弦、弧长计算
例1 在半径为5 cm的圆内有长为5 cm的弦AB,求此弦所对 的圆周角. 解析：如图所示，
【正解】根据题意画出大致示意图如图所示，∠AOB 为弦 AB 所对的圆心角，∠C 和∠D 是弦 AB 所对的圆周角． ∵AB＝OA＝OB， ∴△AOB 为等边三角形， ∴∠AOB＝60°，∴∠C＝30°，∴∠D＝150°， ∴弦 AB 所对的圆心角为 60°，所对的圆周角为 30°或 150°. 易错点：对圆周角的概念理解不清 【疑难点辨析】顶点在圆上且两边都和圆相交的角叫做圆周角，一 条弦所对的圆周角应有两种情况．

圆周角定理PPT课件

圆周角定理PPT课件
关系？
n 为了解决这个问题,我们先探究同弧所对的圆周角和 圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
精选2021最新课件
5
探究同一条弧所对的圆周角和圆心角的关系
1、分别量一量图23.1.10中弧AB所对的两 个圆周角的度数比较一下. 再变动点C在 圆周上的位置，看看圆周角的 度数有没有变化. 你发 现其中有什么规律吗？
C
O.
A
B
顶点在圆上
两边都与圆相交
这样的角叫圆周角。
精选2021最新课件
3
问题探讨：
判断下列图形中所画的∠P是否为圆周角？并说明理
由。
P
P
P
P 不是
顶点不 在圆上。
是
顶点在圆上， 两边和圆相 交。
不是
两边不和 圆相交。
精选2021最新课件
不是 有一边和圆 不相交。
4
类比圆心角 探知 圆周角
• 在同圆或等圆中,同弧或等弧所对的圆心角相等. • 在同圆或等圆中,同弧或等弧所对的圆周角有什么
B
n老师提示:能否转化为1的情况? n过点B作直径BD.由1可得:
AD C
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
2
●O
∴ ∠ABC = ∠1 AOC.
2
B
同弧所对的圆周角等于它所对
你能写出这个命题吗?
的圆心角的一半.
精选2021最新课件
11
圆周角和圆心角的关系 A
C
• 如果圆心不在圆周角的一边上,结果 会怎样?
四边形ABCD的对角线把4个内角分成8个角，
这些角中哪些是相等的角？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 = 2 ∠AOD,∠CBD 1 = 2 ∠COD,
●
C O B
1 ∠ABC = ∠AOC. 2
一条弧所对的圆周角等于它所 一条弧所对的圆周角等于它所 圆周角 对的圆心角的一半. 圆心角的一半 对的圆心角的一半.
议一议
圆周角定理 圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 的大小关系是 一条弧所对的圆周角等于它所对的圆心角 圆周角等于它所对的圆心角的一 圆周角定理 : 一条弧所对的圆周角等于它所对的圆心角的一 1 半.
A E
●
驶向胜利 的彼岸
A E B D
C
O
C
B D
在同圆内,同弧或等弧所对的 在同圆内 同弧或等弧所对的 圆周角相等. 圆周角相等
圆周角定理: 在同一圆内,同弧或等弧所对的圆周角相等 同弧或等弧所对的圆周角相等, 在同一圆内 同弧或等弧所对的圆周角相等 都等于该弧所对的圆心角的一半;相等的圆周 都等于该弧所对的圆心角的一半 相等的圆周 角所对的弧相等． 角所对的弧相等．
●
O D C A
●
O C B
O C
D
70o
B
４．如图：四边形ＡＢＣＤ内接于⊙Ｏ，则 ∠BAD = 如图：四边形ＡＢＣＤ内接于⊙Ｏ，则 ＡＢＣＤ内接于
∠BOD =
例２．ＡＢ是⊙Ｏ的直径，ＢＤ是⊙Ｏ的弦，延 长ＢＤ到点Ｃ，使ＣＤ＝ＢＤ，连接ＡＣ． 判断ＡＢ与ＡＣ的大小有什么关系？为什么？
Ａ
Ｂ
Ｄ
Ｃ
如图：已知ＢＣ为 如图：已知ＢＣ为⊙Ｏ的直径，ＡＤ⊥ＢＣ， ＢＣ 的直径，ＡＤ⊥ ，ＡＤ 垂足为Ｄ，ＢＦ ＡＤ于Ｅ，且 Ｄ，ＢＦ交 垂足为Ｄ，ＢＦ交ＡＤ于Ｅ，且ＡＥ＝ＢＥ． ︵ ︵ 求证：ＡＢ＝ＡＦ （１）求证：ＡＢ＝ＡＦ 3 （２）若sin∠ＦＢＣ＝ , AB = 4 5 , 求AD的长。 ∠
即
Cቤተ መጻሕፍቲ ባይዱ
∠ABC = ∠AOC.
A 2 C
●
A
A C B
●
●
O
O
O
B
B
想一想
圆周角定理:探索2 圆周角定理:探索2
当球员在B,D,E处射门时, 当球员在B,D,E处射门时, B,D,E处射门时 他所处的位置对球门AC 他所处的位置对球门AC 分别形成三个张角∠ 分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角 ∠ADC,∠AEC.这三个角 的大小有什么关系?. 的大小有什么关系?.
1 = 2∠AOD,∠CBD 1 = 2 ∠COD,
●
C O
1 ∴ ∠ABC = ∠AOC. 2
一条弧所对的圆周角等于它所 一条弧所对的圆周角等于它所 圆周角 对的圆心角的一半. 圆心角的一半 对的圆心角的一半.
B
议一议
圆周角和圆心角的关系 圆周角和圆心角的关系
驶向胜利 的彼岸
如果圆心不在圆周角的一边上,结果会怎样? 如果圆心不在圆周角的一边上,结果会怎样? 3.当圆心(O) 圆周角(∠ABC)的外部时, (O)在 (∠ABC)的外部时 3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角 ∠ABC与圆心角∠AOC的大小关系会怎样? A ABC与圆心角∠AOC的大小关系会怎样? 与圆心角 的大小关系会怎样 老师提示:能否也转化为1的情况? 老师提示:能否也转化为1的情况? 过点B作直径BD.由 可得: 过点B作直径BD.由1可得: BD. ∠ABD ∴
想一想
类比圆心角探知圆周角 类比圆心角探知圆周角 探知
A C
●
驶向胜利 的彼岸
圆周角有什么关系 在同圆或等圆中,相等的弧所对的圆周角有什么关系？ 同圆或等圆中 相等的弧所对的圆周角有什么关系？
A A C B B B
●
C
●
O
O O
为了解决这个问题, 为了解决这个问题,我们先探究一条弧所对的圆周 角和圆心角之间有的关系. 角和圆心角之间有的关系.
●
议一议
圆周角和圆心角的关系 圆周角和圆心角的关系
驶向胜利 的彼岸
如果圆心不在圆周角的一边上,结果会怎样? 如果圆心不在圆周角的一边上,结果会怎样? 2.当圆心(O) 圆周角(∠ABC)的内部时, (O)在 (∠ABC)的内部时 2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角 ∠ABC与圆心角∠AOC的大小关系会怎样? A ABC与圆心角∠AOC的大小关系会怎样? 与圆心角 的大小关系会怎样 D 老师提示:能否转化为1的情况? 老师提示:能否转化为1的情况? 过点B作直径BD.由 可得: 过点B作直径BD.由1可得: BD. ∠ABD
23.1.3. 圆周角和圆心角的关系 -圆周角定理
圆周角的定义: 顶点在圆周上,两边和圆相交的角叫做圆周角 两边和圆相交的角叫做圆周角. 顶点在圆周上 两边和圆相交的角叫做圆周角
A
.
B O C
探究活动：有关圆周角的度数
1． 探究半圆或直径所对的圆周角 ． 等于多少度？ 等于多少度？ 的圆周角所对的弦是否是直径？ ２.900的圆周角所对的弦是否是直径？
例题
如图:AB,AC是⊙O的两条弦 延长 到D,使 的两条弦,延长 例1:如图 如图 是 的两条弦 延长CA到 使 ∠ADB = 40o , 求∠BOC的度数。 AD=AB.若 若 B D O
A
C
随堂练习
练习
1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 1.如图, ,∠BOC=50° 的大小. 如图
B C A
●
驶向胜利 的彼岸
O
２．如图，在⊙O中，AB＝AC，∠ＡＢＣ＝ °. 如图， 中 ＝ ， ＡＢＣ＝70° ＢＯＣ度数 度数. 求∠ＢＯＣ度数
︵
︵
(第 2 题)
猜一猜
驶向胜利 的彼岸
３.如图,在⊙O中,∠BAD=50°,求∠C的大小. 如图, ,∠BAD=50° 的大小. A D A
B E
线段AB是 线段AB是⊙O的直径，点C是⊙O AB 的直径， 上任意一点（ 上任意一点（除点A、B）， 那 么，∠ACB就是直径AB所对的圆 周角.想想看， 周角.想想看，∠ACB会是怎么样 的角？为什么呢？ 的角？为什么呢？
结论： 结论：
半圆或直径所对的圆周角都相等，都等于 半圆或直径所对的圆周角都相等， 90°（直角）。反过来也是成立的，即90° 90° 直角）。反过来也是成立的， 90° ）。反过来也是成立的 的圆周角所对的弦是圆的直径
议一议
圆周角和圆心角的关系 圆周角和圆心角的关系
驶向胜利 的彼岸
1.首先考虑一种特殊情况： 首先考虑一种特殊情况： 圆心(O) 圆周角(∠ABC)的一边(BC)上时, (O)在 (∠ABC)的一边(BC)上时 当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角 A ∠ABC与圆心角∠AOC的大小关系. ABC与圆心角∠AOC的大小关系. 与圆心角 的大小关系 C ∵∠AOC是△ABO的外角， ∵∠AOC是 ABO的外角， 的外角 ∴∠AOC=∠B+∠A. O ∵OA=OB， ∵OA=OB， ∴∠A=∠B. B ∴∠AOC=2∠B. 1 一条弧所对的圆周角 圆周角等于它所 一条弧所对的圆周角等于它所 即 ∠ABC = ∠AOC. 2 对的圆心角的一半. 圆心角的一半 对的圆心角的一半.
5
Ａ Ｅ Ｏ
Ｆ
Ｂ
Ｄ
Ｃ
独立作业
挑战自我
驶向胜利 的彼岸
P52 P74