5.3频数与频率
- 格式:doc
- 大小:399.00 KB
- 文档页数:2


5 .3 频数与频率[教学目标](一)教学知识点1.掌握频数、频率的概念.2.会求一组数据的频数与频率.(二)能力训练要求1.通过统计数据,制成各种图表,增强学生对生活中所见到的统计图表进行数据处理和评判的主动意识.2.培养学生利用图表获取信息的能力,使学生能初步把数字信息、图形和语言之间相互转化,并作出合理推断.(三)情感与价值观要求培养学生实事求是的科学态度,并通过对数据的整理,提高学生的责任心与耐心细致的工作态度.[教学重点]频率与频数的概念,选择数据表示方式.[教学难点]各种统计图表的绘制,识别各种图表所含的信息,各自优缺点.[教学方法]合作探讨法[教具准备]挂图或小黑板[教学过程]Ⅰ.导入新课上节课我们主要学习了数据的收集,并探讨了抽样调查时要注意的问题.(1)样本的大小.(2)样本的代表性.(3)样本的广泛性.使所抽取的样本尽可能准确地反映总体的真实情况.本节课我们继续学习统计初步中反映数据出现频繁程度的两个量频数与频率.Ⅱ.讲授新课1.例题讲解同学们,你们平时最喜爱的体育运动是什么?你最喜爱的体育明星是谁?下面是小亮式是什么?你能设计出一个比较好的表示方式吗?小组相互交流,共同探讨.出示挂图(二) [师]此种表示方式的优点是什么?[生]简单明了,一眼可以看出哪个最多、哪个最少.[师]此种表示方式的优点是什么?[生]直观,一目了然.不仅可以很快判断出哪个最多,哪个最少,还可比较出差别是否悬殊很大.[师]从上表可以看出,A 、B 、C 、D 出现的次数有的多,有的少,或者说它们出现的频繁程度不同.我们称每个对象出现的次数为频数。
.而每个对象出现的次数与总次数的比值为频率。
如:A 的频数为23,A 的频率为5023. B 的频数为8,B 的频率为254. C 的频数为13,C 的频率为5013. D 的频数为6,D 的频率为253. Ⅲ . 1、做一做:(课本 P186)2.议一议:(见课本 P186)小明、小亮从同一本书中分别随机抽取了6页,在统计了1页、2页、3页、4页、5页、6页的“的”和“了”出现的次数后,分别求出了它们出现的频率,并绘制了下图图5-1[生]频率在0.05至0.06之间变化的字是“的”字.“了”字的频率在0.005至0.015之间变化.[师]你认为该书中“的”和“了”两个字使用的频率哪个高?[生]我认为是“的”字.Ⅳ.课时小结本节课主要学习了如下内容.1.频数与频率两个基本概念.2.会求一组数据的频数与频率,并会选择合理的表示方式来表示数据.例用频数分布直方图、图表、扇形区域分布图等表示所收集的数据情况.Ⅴ.课后作业习题5.3 1.2.[联系拓广] P188 第 3、4 题[教学反思]。

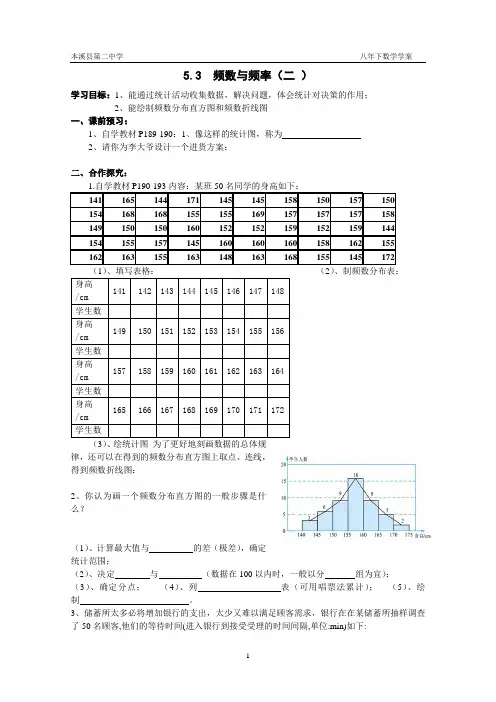
5.3 频数与频率(二)学习目标:1、能通过统计活动收集数据,解决问题,体会统计对决策的作用;2、能绘制频数分布直方图和频数折线图一、课前预习:1、自学教材P189-190:1、像这样的统计图,称为2、请你为李大爷设计一个进货方案:二、合作探究:律,还可以在得到的频数分布直方图上取点、连线,得到频数折线图:2、你认为画一个频数分布直方图的一般步骤是什么?(1)、计算最大值与的差(极差),确定统计范围;(2)、决定与(数据在100以内时,一般以分组为宜);(3)、确定分点;(4)、列表(可用唱票法累计);(5)、绘制。
3、储蓄所太多必将增加银行的支出,太少又难以满足顾客需求,银行在在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:15 20 18 3 25 34 6 0 17 24 23 30 35 42 37 24 21 1 1412 34 22 13 34 8 22 31 24 17 33 4 14 23 32 33 28 42 2514 22 31 42 34 26 14 25 40 14 24 11(1)这组数据的极差是;(2)可以将数据分为组,组距为;(3)确定分点;(4)列频数分布表;(5)绘频数分布直方图。
学习小结:画频数分布直方图(折线图)要注意些什么?三、反馈练习1、一个样本含有下面10个数据:52,51,49,50,47,48,50,51,48,53,则最大的值是_________,最小的值是_________,如果组距为1.5,则应分成________组.(30′)2、某技校对所属文秘专业的90名学生进行打字速度测试,测试结果见表格与频数分布直方图.请补全表格与频数分布直方图(30′)3、某地区抽调了一部分市民进行了一次法制观念知识竞赛,竞赛成绩(得分取整数)进行整理后分成五组,并绘制成频率分布直方图,请解答下列问题:(40′)(1)抽取了多少人参加竞赛?(2)60.5-70.5这一分数段的频数、频率分别是多少?(3)这次竞赛成绩的中位数落在哪个分数段内?.(4)根据统计图,请你提出一个问题,并回答你所提出的问题.四、反思:。

课题:§5.3频数与频率(二)【学习目标】1.了解频数分布的意义,会得出一组数据的频数分布2.会绘制频数分布直方图与频数分布折线图.3.初步经历数据的收集与处理的过程,发展初步的统计意识和数据处理能力.【学习重点】学会绘制出一组数据的频数分布直方图、频数分布折线图.【学前准备】如何收集与处理数据.(1)(2)(3)(4)【师生探究、合作交流】看课本P189页你能否帮卖雪糕的李大爷设计一种方案,确定各种牌子的雪糕应进多少?想一想: 小丽统计了近一星期李大爷平均每天能卖出的A、B、C、D、E五个牌子雪糕的数量。
雪糕数量频数频率A 131 131 0.253B 182 182 0.351C 68 68 0.131D 39 39 0.075E 98 98 0.190合计518 518 1.000根据上表绘制一张频数分布直方图.(如下)分析:根据小丽的统计结果,A占总数的,B占总数的 ,C占总数的,D占总数的,E占总数的为李大爷设计一个进货方案,两种雪糕卖出的较多,可以多进些,种雪糕卖出的少,可以少进些。
确定进货的总数,还应考虑,当天气温情况.做一做[例]学校要为同学们订制校服,为此小明调查了他们班50名同学的身高,结果(单位 cm).如下:141 165 144 171 145145 158 150 157 150 154 168 168 155 155169 157 157 157 158 149 150 150 160 152152 159 152 159 144 154 155 157 145 160160 160 158 162 155 162 163 155 163 148163 168 155 145 172填写下表,并将上述数据用适当的统计图表示出来.小亮的做法.将数据分成一下几组,并得到相应各组的学生人数:144 cm以下 145~149 cm 150~154 cm 155~159 cm3 6 9 16160~164 cm 165~169 cm 170 cm以上9 5 2根据上表绘制出频数分布直方图:当收集的数据连续取值时,我们通常将数据分组,然后再绘制频数分布直方图. 绘制连续型频数分布直方图的步骤:(1)计算极差(最大值与最小值的差);(2)决定组距(每个小组的两个端点之间的距离)与组数;当数据在100个以内时,通常分成5-12组,组距通常取整数(3)确定分点;(4)列频数分布表;(5)画频数分布直方图.为了更好地刻画数据的总体规律,我们还可以在得到的频数分布直方图上取点、连线,得到如下的频数分布折线图.比较一下各种统计图各自的优缺点.表一:.表二,优点. :.缺点:. .图5-3、图5-4能直观形象地将数据表示出来,而且能刻画出数据的总体规律.中间人数较集中,两边较少.【课堂小结】1.如何整理所收集的数据.2.将数据用适当的统计图表示出来.(1)表格形式.(2)频数分布直方图(3)频数分布折线图.3.各种统计图、表的优缺点.4.根据统计图表信息,提出合理化建议.【课后作业】P193页1, 习题5.4 2.。



《5.3.1频数与频率》问题导读—评价单1.知识与能力:①理解频数、频率等概念,并能读懂相应的频数分布直方图和频数折线图;②体会用样本估计总体的思想.2.过程与方法:①能根据数据处理的结果,作出合理的判断和预测.②进一步发展学生的统计思想3.情感态度与价值观:培养学生用科学的态度进行统计活动.(三)学习重、难点重点:理解频数、频率的概念并绘制出相应的统计图表,从而作出合理的判断和预测。
难点:正确列出统计图有。
(四)学习流程预习教材第 184 至 186 页内容后,完成下列问题。
1.频数的定义:频率的定义:频数与频率的关系:2.调查我们班每一位同学喜欢下列六门学科中的哪一门?并用枚举法表示出来,(如用P表示政治,C表示表示语文,M表示数学,E表示英语,Ph表示物理,S表示体育),这种数据表示方式好不好?如果让你直观的表现出哪科喜欢的人数多或少,有什么办法?3.想一想,你认为那个汉字的使用频率最高?设计一个简单的调查方案,粗略地估计一下它的使用频率,并将调查结果在全班交流。
4.设计“通过预习本节内容你未解决的问题有:自我评价:小组评价:教师评价:各位同学,请在预习的基础上,将生成的问题系统思考后,在小组内充分交流,并在单位时间内认真完成下列问题,经过合作探究后准备多元化展示. “问题”展示问题1:频数一般都有什么样的特征,那频率呢?问题2:东东连续记录了10天以来爸爸每天看报纸的时间,结果如下(单位:分)12,20,16,20,22,18,19,16,20,23,那么出现频率最高的时间是,它出现的频数是,频率是。
问题3:将一组数据分为5组,列出频数分布表,其中第一组的频数是2 0,频率是0.2,第二组的频率为0.3,那么这组数据共有数据个,第三、四、五组的频率之和为,第二组的频数为。
问题4:学习拓展P61 1问题5:课本P187 1问题6:学习拓展P61 4从今天的课程中,你学到了什么知识?小组评价:教师评价:班级:姓名:基础演练1.在频数分布表中,各小组的频数之和()A 小于数据总数B 等于数据总数C 大于数据总数D 不能确定2.下列说法正确的有()A 频数越大,频率越大B 频数越小,频率越大C 总数一定的情况下,频数越大,频率越大D 总数一定的情况下,频数越小,频率越大3.已知样本18,20,20,18,16,23,21,20,22,19,17,18,22,19,21,22,19,20,20,21,那么频率为0.2的范围是()A 16~18B 18~20C 20~22D 22~244.在某校九年级的一次化学测试中,化学测试成绩在80—84分之间的同学有84人,在频率分布表中的频率为0.35,则全校九年级共有学生_______人5.某中学一位同学调查了八年级60名学生观看自己最喜爱的电视节目的情况,其中有10人爱看动画片,15人爱看连续剧,23人爱看体育节目,12人爱看新闻节目.在上面问题中,________分别为各节目出现的频数,其中爱看动画片的频率约为________能力拓展某市对当年初中升高中数学考试成绩进行抽样分析,试题满分100分,将所得成绩(均为整数)整理后,绘制了如图所示的统计图,根据图中所提供的信息,回答下列问题:(1)共抽取了多少名学生的数学成绩进行分析?(2)如果80分以上(包括80分)为优生,估计该年的优生率为多少?(3)该年全市共有22000人参加初中升高中数学考试,请你估计及格(60分及60分以上)人数大约为多少小组评价:教师评价:。

5.3频数与频率课前准备重点:频数与频率的概念,选择数据表示方式。
难点:各种统计图表的绘制,识别各种图表所含的信息及它们各自的优点。
学习准备1.什么是普查?什么是抽样调查?2.什么情况采用普查?什么情况采用调查?课中导学阅读感知阅读课本184-185页,回答下列问题1.在小明的调查结果中A出现了次,与总次数的比值是,由于A出现次数比例比较大,我们可直观看出,但B与A谁出现的次数多,我们能直观看出吗?2.小丽根据小亮的结果制成的图(如图1),是否可以直观看出B和D谁出现的次数多呢?这个图有什么优点?从图1可以看出,A、B、C、D出现的次数有多有少,或者说它们出现的频繁程度不同。
我们称每个对象出现的次数为,而每个对象出现的次数与总次数的比值为。
3.分别计算A、B、C、D的频数与频率。
A的频数为A的频率为;B的频数为B的频率为;C的频数为C的频率为;D的频数为D的频率为;思考:频数与频率有什么关系?合作探究设计一个方案,了解你们班同学最喜欢的科目是哪科,为什么喜欢?(1)分析:先列表,再统计,调查探讨最喜欢的原因。
调查不爱学的那门科目的原因。
列表如下:(2)你还能用阅读感知中图1的形式表示上面的数据吗?请在下面完成。
练习巩固调查你们学校300名同学喜欢足球、篮球、乒乓球、羽毛球的情况,并在调查到50名、100名、150名、200名、250名、300名时分别计算喜欢4种球的频率,并绘制如教材186页图5-5的图,随着调查次数的增加,喜欢足球的频率是如何变化的?你能估计调查500名同学时,喜欢足球的频率是多少吗?反思感悟本节课主要学习了:1. 与 两个基本概念。
2. 会求一组数据的 与 ,并会选择合理的表示方式来表示数据。
课后巩固1. 已知数据:,3,2,31π,-2其中无理数出现的频率为( ) A20% B40% C 60% D 80% 2. 如图2,是1998年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于60的国家个数是( ) A 4 B 8 C 10 D 12 3.王老师为了了解本班学生课业负担情况在班中随机调查了10名学生,他们每人上周平均每天完成家庭作业所用的时间分别是(单位:小时):1.5,2,2,2,2.5,2.5,2.5,2.5,3,3.5,,则这10个数据中2.5出现的频数是 ,频率是 ;2出现的频数是 ,频率是 ;1.5频数是 ,频率是 ;3.5频数是 ,频率是 ;3现的频数是 ,频率是 ; 4.某中学为了了解学生的课外阅读情况。


5.3 频数与频率(第二课时)一、教学目标(一)知识与技能:经历数据收集,进行简单的数据整理,由推理过程感受抽样的必要性;能根据数据绘制相应的频数分布直方图和频数分布折线图。
(二)过程与方法:经历收集、处理数据的过程,进一步了解频数与频率在实际生活中的应用,通过绘图,进一步掌握数形结合的思想方法。
(三)情感与能力:能根据数据处理的结果,做出合理的判断和预测,从而解决实际问题,并在这一过程中体会统计对决策的作用。
经历自主探究、合作交流等学习方式的学习及激励评价,让学生在学习中锻炼能力,培养良好的情感、态度和价值观。
(四)教学重点:绘制频数分布直方图和频数分布折线图。
(五)教学难点:将一组数据正确地进行分组并列频数分布直方图。
二、教材分析本节内容选于《义务教育课程标准实验教科书—数学》(北师大版)八年级(下)第五章第3节,本章在已学习“数据的代表”的基础上,以理解频数、频率的概念为核心内容,为下一节课学习“数据的波动”作好准备。
前3册的学习中,学生已经初步经历了一些数据收集的过程,获得了一些数据收集与处理的活动经验。
但对于数据收集的方法,学生尚多是凭借一些生活的经验,对此缺乏一种理性的思考。
为此,本章将介绍数据收集的两种常用方法-----普查和抽样调查,并希望通过实际问题的讨论,让学生明确两种方式的特点,从而能够具体情境的要求中选用适当的调查方式。
在八年级上学期,学生已经研究过刻画数据“平均水平”的几个尺度,具备了一定的数据处理的能力。
但仅有“平均水平”,还难以准确地刻画一组数据。
为此,本节又介绍了刻画数据几个量——频数与频率。
本节课重在学生自己动脑、动手,培养创造精神和探究意识,因而在教学中,教师要热情鼓励学生自主探究和大胆创新,对每一位同学作品给予鼓励和足够的重视。
三、学生情况分析1、学生已在八上初步学习了“数据的代表”等基本知识,同时结合农村初中学生实际,探讨生活中的实际问题。
深入三峡坝区调查个体户经营情况,进行数据收集与处理。
频数与频率优秀教案篇1:频数与频率优秀教案频数与频率优秀教案教学目标(一)教学知识点1.如何收集与处理数据.2.会绘制频数分布直方图与频数分布折线图.3.了解频数分布的意义,会得出一组数据的频数分布.(二)能力训练要求1.初步经历数据的收集与处理的过程,发展学生初步的统计意识和数据处理能力.2.通过经历调查、统计、研讨等活动,发展学生实践能力与合作意识.(三)情感与价值观要求通过学习,培养学生勇于提出问题,大胆设计,勇于探索与解决问题的能力.教学重点1.了解频数分布的意义,会得出一组数据的频数分布直方图、频数分布折线图.2.数据收集与处理.教学难点1.决定组距与组数.2.数据分布规律.教学方法交流探讨式教具准备投影片教学过程Ⅰ.导入新课[师]请大家一起回忆一下,我们如何收集与处理数据.[生]1.首先通过确定调查目的`,确定调查对象.2.收集有关数据.3.选择合理的数据表示方式统计数据.4.根据所收集的数据进行数据计算.根据特征数字,估计总体情况,设计可行的计划与方案,并不断实施与改进方案.[师]这位同学总结得很好.你能否帮卖雪糕的李大爷设计一种方案,确定各种牌子的雪糕应进多少?[生]首先应开展调查.统计一下李大爷每天卖出的A、B、C、D、E五个牌子雪糕的数量.篇2:频数与频率-频数与频率(第二课时)湖北省丹江口市丹赵路中学设计:王世涛教学内容课题名称频数与频率学科数学总课时数1版本名称湖南教育出版社年级八年级册次上册单元章节名称第四章页码119面执教者陈毅学习目标:1、知识与技能(1)了解频数与频率的概念。
(2)会进行统计活动,并计算频率。
2、过程与方法(1)让学生从现实生活实例中抽象出频数与频率的概念。
(2)让学生经历统计活动的过程,理解整理数据的方法及必要性。
3、情感、态度与价值观通过实践操作、巩固学生对各种图表信息的识别与获取信息的能力,增强学生对生活中所见的统计图表进行数据处理和评判意识。
5.3频数与频率2课前准备重点:1.了解频数分布的意义,会得出一组数据的频数分布直方图、频数分布折线图。
2.数据收集与处理。
难点:1.决定组距与组数。
2.数据分布规律。
学习准备1.什么是频数和频率?什么是平均数?2.什么是条形统计图?什么是折线统计图?课中导学阅读感知1.阅读课本189-192页,回答下列问题像图1这样的统计图称为。
思考:频数分布直方图有什么联系和区别?2.(1)同学们想一想,你同父母一起去商店买衣服时,看到有些衣服上标有M、S、L、XL、XXL等号码吗,标志是什么?是否与身高有关?(2)厂家做衣服订尺寸也不是按所有人的尺寸定做,而是按某个范围分组批量生产,如何确定组距与级数呢?合作探究小组合作:参照小亮的做法,总结一下绘制连续型频数分布直方图的一般步骤:(1)计算最大值和最小值的,确定统计量的范围;(2)决定和。
(3)确定分点,为了保持组距相等,往往会把最小值减小一点作为最左端的分点,把最大值加大一点作为最右端的分点,两边上组距也可以与其他组距不相等。
(4)列频数分布表;(5)画频数分布直方图。
练习巩固某次数学能力测试中,八(1)班48名同学的测试成绩(单位:分)如下:60,64,67,66,65,69,64,67,63,65,63,67,70,70,76,78,75,74,77,76,78,75,78,74,73,79,80,75,76,76,73,70,78,78,76,75,75,85,81,80,82,84,81,89,95,92,85,86。
如果将同学们成绩x(分)分成合格(60≤x<75),良好(75≤x<90),优秀(x≥90)三类,那么请你求出三类成绩等级的频数,并绘制成相应的频数分布直方图品种图1反思感悟1. 如何整理所收集的数据2. 如何频数分布直方图和频数折线图。
课后巩固1.某校为了了解九年级学生的体能情况随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在15-20次之间的频率是( ) A0.1 B0.17 C0.33 D0.42.九年级(10班共50名学生,图3是该班体育成模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数)。
5.3频数与频率(一)(课本P184~188)学习目标:1、理解频数、频率等概念;2、会对一组数据进行统计,并绘制出相应的统计图表;3、能根据数据处理的结果,作出合理的判断与预测。
中心问题:如何对调查收集的数据进行处理?预习过程:一、基础知识回顾:1.通过前面的学习,我们可以知道:普查可以直接获得总体情况,但有时总体中个体数目较,普查的工作量;有时受客观条件的限制,无法对所有个体进行普查;有时调查具有破坏性,(填“允许”或“不允许”)普查。
此时,可以采用调查。
通过样本的特征数字可以总体情况。
二、新知识产生过程:1、在课本第184页的例子中,这种数据统计方式(填“好”或“不好”).因为这种表示方法。
我们可以画表示2、每个对象出现的叫做频数,每个对象出现的与的比值叫做频率。
例如:在“I love China”中字母“i”出现的频数为,频率为。
在实际统计过程中,我们常常用写“”字的方式来统计,因为一个“”字表示的频数为。
3.完成课本P186 “议一议”三、例题学习:例1 要反映一天内气温的变化情况,宜采用()A、条形统计图B.扇形统计图C.频数分布图D.折线统计图(三)巩固练习四、巩固练习:1、今年3月份,某市教育局倡导中小学开展“4312”(“4312”即“四操”、“三球”、“一跑”“二艺”活动的简称)艺体普及活动。
某校学生会为了了解全校同学对“4312”中部分项目的喜爱情况,随机调查了200名同学(每名同学仅选一项最喜爱的项目),并根据调查结果制作了频数分布表:(1)请补全频数分布表。
(2)在这次抽样调查中,最喜爱哪个体育项目的同学最多?最喜爱哪个体育项目的同学最少:(3)根据以上调查,试估计该校1620名同学中最喜爱健美操的人数。
5.3 频数与频率
学习目标
1.掌握频数、频率的概念.
2.会求一组数据的频数与频率.
3.了解频数分布的意义,会得出一组数据的频数分布.
教学重点
频率与频数的概念,选择数据表示方式. 会得出一组数据的频数分布直方图、频数分布折线图.
教学难点
决定组距与组数.数据分布规律. 绘制各种统计图表,识别各种图表所含的信息,各自优缺点.
导学:
下面是小亮调查的八(1)班50位同学喜欢的足球明星,结果如下:(投影片)
根据上面结果,你能很快说出该班同学最喜欢的足球明星吗?他的数据表示方式是什么?
这些数据没有经过统计、整理,必须把A、B、C、D的个数全部数清,才能比较出哪位球星是该班同学最喜欢的.数据越多越不方便,所以我认为小亮的数据表示方式不太好.
[师]你能设计出一个比较好的表示方式吗?小组相互交流,共同探讨.
[生]我们小组用如下方式表示
[师]从上表能够看出,A、B、C、D出现的次数有的多,有的少,或者说它们出现的频繁水准不同.我们称每个对象出现的次数为频数(absolute,frequency).而每个对象出现的次数与总次数的比值为频率(relative frequency).
[师]分别计算A、B、C、D的频数与频率.
A的频数为23,A的频率为______B的频数为______,B的频率为______C的频数为______,C的频率为______D的频数为______,D的频率为______
练习
1.在对n个数据实行整理的频率分布表中,各组的频数与频率之和分别等于()
A.n,1
B.n,n
C.1,n
D.1,1
2.扇形统计图中,扇形A.B.C.D的面积之比为2∶1∶4∶5,则最大扇形的圆心角为()
A.80°
B.100°
C.120°
D.150°
3.某地上半年每月的平均气温是5℃,8℃,12℃,18℃,24℃,30℃,为了表示出气温变化的情况能够把它绘制成()
A.扇形统计图
B.折线统计图
C.条形统计图
D.以上都能够
4.一个样本含有下面10个数据:52,51,49,50,47,48,50,51,48,53,则最大的值
是_________,最小的值是_________,如果组距为1.5,则应分成________组.
5.在数据55,66,23,33,22,65,84,87,23,24,88中,大于等于50而小于等于70
的数共有_________个
6.在扇形统计图中,有两个扇形的圆心角度数之比为3∶4,且较小扇形表示24本课本书,
则较大扇形表示________本课本书.
7.一组数据共50个,分别落在5个小组内,第一.二.三.四组的数据分别为2.8.15.20,则第五小组的频数和频率分别为________._________.
8.如图是两户居民家庭全年各项支出的统计图.根据统计图,下列对两户教育支出占全年总
支出的百分比作出的判断中,准确的是()
A.甲户比乙户大
B.乙户比甲户大
C.甲.乙两户一样大
D.无法确定
哪一户大
9.某中学一位同学调查了八年级60名学生观看自己最喜爱的电视节目的情
况,其中有10人爱看动画片,15人爱看连续剧,23人爱看体育节目,12人爱
看新闻节目.在上面问题中,__________________________分别为各节目出
现的频数,其中爱看动画片的频率约为__________________________.
10.在扇形统计图中,其中有一个扇形的圆心角为108°,那么这个扇形所表示的
部分占总体的百分比是___________.
11.某市有5类学校,各类学校占总校数的百分比如下:
学校幼儿园小学中学特殊教育高等院校
百分比36%32%22%4%6%
(1)计算各类学校对应的扇形圆心角度数;
(2)画扇形统计图来表示上面的信息;
(3)哪两类学校较多?各占百分比是多少?
(4)若高等院校有42所,则该市共有学校多少所?中学有多少所?
小结与反思:
_______________________________________________________________________________ _______________________________________________________________________________。