2016届山西省忻州一中、长治二中、康杰中学、临汾一中联考高三(上)第一次月考生物试卷【解析版】

山西省忻州一中、长治二中、康杰中学、临汾一中2016届高三上学期第一次联考试题第Ⅰ卷(单项选择题，每题2分共50分)1．下表所列原核细胞与真核细胞的比较，正确的是372的有机产物，其中脱下的氨基酸均以游离态正常存在。

下列该过程产生的全部有机物中有关原子、基团或肽键数目的叙述，错误的是A．肽键数目减少6个B．氢原子数目增加12个C．氨基和羧基分别增加3个D．氧原子数目增加6个3．正常人体内的胰岛素、呼吸酶和抗体，这三类物质都是A．在胰岛B细胞中合成B．通过胞吐的方式释放C．与特定的分子结合后发挥作用D．在细胞间进行信息交流4．下列与细胞器相关的叙述中，正确的是A．蓝藻细胞中有的酶在核糖体上合成后，再由内质网和高尔基体加工B．分泌蛋白合成旺盛的细胞中，高尔基体膜成分的更新速度快C．溶酶体能吞噬并杀死侵入细胞的病毒或病菌，但不能分解衰老的细胞器D．植物细胞叶绿体产生的A TP主要用于主动运输等过程5．下列关于染色体和染色质的叙述中，错误的是A．染色质是细胞核中容易被碱性染料染成深色的物质B．基因可能存在于染色体上，也可能存在于其他场所C．蓝藻细胞在进行有丝分裂时不出现染色体D．染色体和染色质是同一种物质在不同时期的两种状态6．将小鼠红细胞放入一定浓度的KNO3 溶液中，红细胞体积随时间变化如图，有关叙述正确的是A．KNO3 溶液的起始渗透压小于红细胞内液的起始渗透压B．与B点相比，A点对应时刻红细胞内液的渗透压较大C．AB段失水使红细胞内液的渗透压大于KNO3 溶液，从而出现BC段的变化D．B点对应的时刻，KNO3 溶液与红细胞内液的渗透压相等7．下列关于酶的叙述正确的是A．酶是由腺细胞合成的具有催化作用的有机物B．所有酶用双缩脲试剂进行检测都可以呈现紫色反应C．酶分子在催化反应完成后立即被降解成氨基酸D．消化酶在消化腺细胞内合成并分泌到细胞外的过程中共穿过0层磷脂双分子层8．A TP是细胞内流通的能量“通货”，下列关于ATP的说法中，错误的是①参与ATP形成的元素包括C、H、O、N、P②在叶绿体中，A TP的移动方向是由叶绿体的囊状结构到叶绿体基质③洋葱表皮细胞中能形成ATP的细胞器有线粒体和叶绿体④A TP是各种活细胞内普遍存在的一种高能磷酸化合物，是细胞内唯一的直接能源物质A．①③B．③④C．②③D．②④9．夏季晴朗的中午，某些植物因为蒸腾过于强烈而出现气孔关闭的现象，这是植物对环境变化的一种适应，此时这些植物叶肉细胞内C3、C5、[H]、ATP的含量短期变化分别是A．降低、升高、升高、升高B．升高、降低、降低、降低C．降低、升高、降低、降低D．升高、降低、升高、升高10．图1是“质壁分离和复原实验”的部分操作图，图2是“叶绿体中色素分离”的结果，以下相关说法不．正确的是A．盖玻片下最好是成熟的植物组织细胞B．实验中用吸水纸引流常需要重复几次C．图2中b代表的是叶绿素bD．出现图2结果的原因可能是研磨时没加碳酸钙11．如图是化合物在生物体内转移的过程，下列分析正确的是A．①产生的[H]可在②过程中将五碳化合物还原B．[H]经⑤转移到水中，其过程需CO2参与C．能形成ATP的过程有①②④⑤⑥⑦D．晴天时小麦①过程比在阴雨天时旺盛12．小鼠体细胞培养过程中，发现细胞分为3种类型：甲类细胞核DNA量为4a，乙类细胞核DNA量为2a，丙类细胞核DNA量为2a～4a。

2016届高三年级第一次四校联考英语试题命题:长治二中忻州一中临汾一中康杰中学（考试时间120分钟，满分150分）第Ⅰ卷第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the man probably like?A. Playing basketball.B. Rock-climbing.C. Swimming.2. What does the man mean?A. Jane is eager to return home.B. Jane is on her way home.C. Jane won’t spend Christmas at home.3. What can we learn from the conversation?A. The man missed the lecture completely.B. The man was late for the lecture.C. The man doesn’t attend the lecture.4. Why doesn’t the girl lend a pen to the boy?A. She does not have any pens.B. She left her pen at home.C. She has only one pen and has to use it.5. What does the woman do?A. An engineer.B. An official.C. A teacher．第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

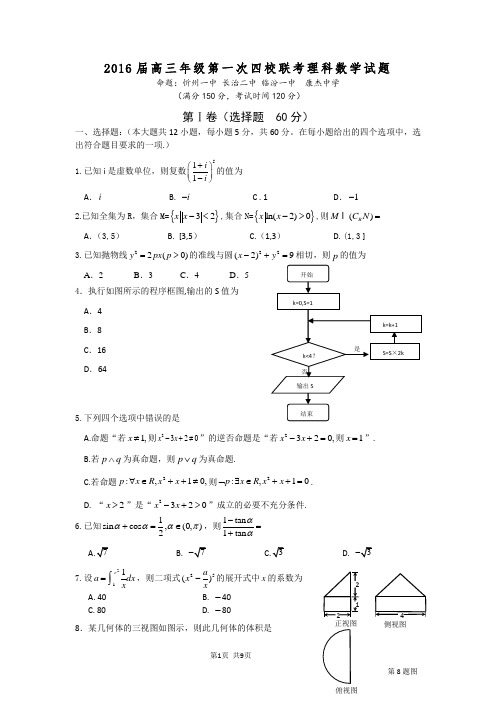
侧视图正视图2016届高三年级第一次四校联考理科数学试题命题：忻州一中 长治二中 临汾一中 康杰中学（满分150分，考试时间120分）第Ⅰ卷（选择题 60分）一、选择题：（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，选出符合题目要求的一项.）1.已知i 是虚数单位，则复数511i i +⎛⎫⎪-⎝⎭的值为A ．i B. i - C . 1 D ．1- 2.已知全集为R ，集合M={}32x x -<,集合N={}ln(2)0x x ->,则()R MC N =A ．（3,5） B. [3,5） C.（1,3） D .(1,3 ] 3.已知抛物线22(0)y px p =>的准线与圆22(2)9x y -+=相切，则p 的值为 A ．2B ．3C ．4D ．5 4．执行如图所示的程序框图,输出的S 值为A ．4B ．8C ．16D ．645.下列四个选项中错误的是A.命题“若1,x ≠则2320x x -+≠”的逆否命题是“若2320,x x -+=则1x =”.B.若p q ∧为真命题，则p q ∨为真命题.C.若命题2:,10,p x R x x ∀∈++≠则2:,10p x R x x ⌝∃∈++=.D. “2x >”是“2320x x -+>”成立的必要不充分条件. 6.已知1sin cos ,(0,)2αααπ+=∈，则1tan 1tan αα-=+B. D. 7.设211e a dx x=⎰，则二项式25(ax x -的展开式中x 的系数为A. 40B. -40C. 80D. -808．某几何体的三视图如图示，则此几何体的体积是A ．20π3B ．6πC ．10π3D ．16π39．函数()2cos()(0)3f x x πωω=+>的图像与x 轴交点的横坐标构成一个公差为2π的等差数列，要得到函数()2sin g x x ω=的图像，只需将函数()f x 的图像A ．向左平移12π个单位长度 B ．向右平移6π个单位长度 C ．向右平移512π个单位长度 D ．向左平移3π个单位长度10．一盒中有白、黑、红三种颜色的小球各一个，每次从中取出一个，记下颜色后放回，当三种颜色的球全部取出时停止取球，则恰好取5次球时停止取球的概率为 A.1481B.2081 C. 2281 D. 258111.在ABC ∆中,角,,A B C 所对的边分别为,,,a b c S 表示ABC ∆的面积，若cos cos sin a B b A c C +=，2221()4S b c a =+-，则B =A ．30 B ．45 C ．60 D ．9012. 已知定义在R 上的奇函数()f x ，其导函数为()f x '，当(0,)x ∈+∞时，恒有()()xf x f x '<-.若()()g x xf x =,则满足(1)(12)g g x >-的实数x 的取值范围是A ．(0,1)B ．(,0)(1,)-∞+∞ C ．(0,)+∞ D ．(,0)-∞第Ⅱ卷（非选择题 90分）二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的相应位置上) 13. 若12,e e 是两个不共线的单位向量，若12e e -与12ke e +垂直，则实数k = ．14．设变量x ，y 满足36020,3x y x y y +-≥⎧⎪--≤⎨⎪≤⎩则变量1y z x =+的最大值为 ．15. 三棱锥P ABC -的四个顶点均在同一球面上，其中△ABC 为等边三角形，PA ⊥平面ABC ，22PA AB a ==,则该球的体积是 ．16. 若对于曲线()x f x e x =--（e 为自然数对数的底数）的任意切线1l ，总存在曲线()2cos g x ax x =+的切线2l ，使得12l l ⊥，则实数a 的取值范围为 ．三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤，并把解答写在答卷纸的相应位置上)17. (本小题满分12分)已知数列{}n a 的前n 项和n S 满足：2,n S an bn =+且121,3a a ==（1）求数列{}n a 的通项公式; （2）记11n n n b a a +=⋅，求数列{}n b 的前n 项和n T .18．(本小题满分12分) 如图，三棱柱111ABC A B C -中， 1AA ⊥面ABC ， BC AC ⊥,2BC AC ==,13AA =,D 为AC 的中点.（1）求证： 1AB //面1BDC ； （2）求二面角1C BD C --的余弦值.19. (本小题满分12分) 在一次抽奖活动中，有甲、乙等6人获得抽奖的机会。

2015-2016学年山西省忻州一中、长治二中、康杰中学、临汾一中高三（上）第一次联考数学试卷（文科）一、选择题（60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B铅笔涂黑答题纸上对应题目的答案标号.）1．已知集合A={x|y=x﹣1}，B={y|y=x2﹣1}，则A∩B=（）A．∅B．{（0，﹣1），（1，0）} C．[﹣1，+∞）D．{0，1}2．已知=（5，6），=（sinα，cosα），已知向量且∥，则tanα=（）A．B．﹣C．D．﹣3．若复数z满足（z+1）i=2﹣i，则复数z的共轭复数在复平面上所对应点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限4．从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，这个点在圆x2+y2=2016内部的概率是（）A．B．C．D．5．已知双曲线的渐近线方程为y=±x，且经过点（4，1），则双曲线的标准方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．各顶点都在一个球面上的正四棱柱的高是2，体积是16，则这个球的表面积是（）A．16π B．20π C．24π D．32π7．设等差数列{a n}的公差是d，其前项和是S n，若a1=d=1，则的最小值是（）A．B．C．2+D．2﹣8．已知a，b∈R+，函数f（x）=alog2x+b的图象经过点（4，1），则+的最小值为（）A．6﹣2B．6 C．4+2D．89．对一名学生数学成绩统计了8次，第i次统计得到的数据为a i，具体如下表所示：在对上述统计数据的分析中，一部分计算见如图所示的算法流程图（其中是这8个数据的平均数），则输出的S的值是（）A．9 B．8 C．7 D．610．对任意的实数x都有f（x+2）﹣f（x）=2f（1），若y=f（x﹣1）的图象关于x=1对称，且f（0）=2，则f（2015）+f（2016）=（）A．0 B．2 C．3 D．411．一个几何体的正视图和俯视图如图所示，其中俯视图是边长为2的正三角形及其内切圆，则侧视图的面积为（）A．6+π B． C．6+4πD．12．函数f（x）=，若方程f（x）=﹣x+a有且只有两个不等的实数根，则实数a的取值范围为（）A．（﹣∞，0）B．[0，1）C．（﹣∞，1）D．[0，+∞）二、填空题（本大题共4小题，每小题5分，共20分）13．函数f（x）=xe x的图象在x=1处的切线方程为．14．若x，y满足约束条件，则z=2x+y的最大值为．15．已知抛物线y2=﹣2px（p＞0）的准线与圆（x﹣5）2+y2=25相切，则p的值为．16．函数f（x）=sinx﹣acosx的图象的一条对称轴是x=，则g（x）=asinx+cosx=Asin （ωx+φ）（A＞0，ω＞0，|φ|≤）的初相是．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．在△ABC中，角A、B、C的对边分别为a、b、c．已知a+b=5，c=，且．（1）求角C的大小；（2）求△ABC 的面积．18．已知在四棱锥S ﹣ABCD 中，四边形ABCD 是菱形，SD⊥平面ABCD ，P 为SB 的中点，Q 为BD 上一动点．AD=2，SD=2，∠DAB=．（Ⅰ）求证：AC⊥PQ；（Ⅱ）当PQ∥平面SAC 时，求四棱锥P ﹣AQCD 的体积．19．（Ⅰ）如表所示是某市最近5年个人年平均收入表节选．求y 关于x 的回归直线方程，并估计第6年此市的个人年平均收入（保留三位有效数字）．其中x i y i =421， x i 2=55附1： =， =﹣（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表：完成上表，并回答：是否有95%以上的把握认为“收入与接受培训时间有关系”． 附2：附3：K2=．（n=a+b+c+d）20．已知椭圆C满足：过椭圆C的右焦点F（，0）且经过短轴端点的直线的倾斜角为．（Ⅰ）求椭圆C的方程；（Ⅱ）设O为坐标原点，若点A在直线y=2上，点B在椭圆C上，且OA⊥OB，求线段AB长度的最小值．21．己知函数f（x）=（a+1）lnx+x﹣，其中a∈R．（I）求f（x）的单调区间；（Ⅱ）若在[1，e]上存在x0，使得f（x0）＜0成立，求a的取值范围．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一个计分.【选修4-1几何证明选讲】22．如图，过圆外一点P的直线交圆O于A、B两点，PE是圆O的切线，CP平分∠APE，分别与AE、BE交于点C，D．求证：（1）CE=DE；（2）=．【选修4─4：坐标系与参数方程选讲】23．设平面直角坐标系原点与极坐标极点重合，x轴正半轴与极轴重合，若已知曲线C的极坐标方程为ρ2=，点F1、F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．（Ⅰ）求曲线C的标准方程和直线l的普通方程；（Ⅱ）若点P为曲线C上的动点，求点P到直线l的最大距离．【选修4-5：不等式选讲】24．设函数f（x）=|2x﹣1|，x∈R．（Ⅰ）求不等式|f（x）﹣2|≤5的解集；（Ⅱ）若g（x）=的定义域为R，求实数m的取值范围．2015-2016学年山西省忻州一中、长治二中、康杰中学、临汾一中高三（上）第一次联考数学试卷（文科）参考答案与试题解析一、选择题（60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B铅笔涂黑答题纸上对应题目的答案标号.）1．已知集合A={x|y=x﹣1}，B={y|y=x2﹣1}，则A∩B=（）A．∅B．{（0，﹣1），（1，0）} C．[﹣1，+∞）D．{0，1}【考点】交集及其运算．【专题】集合．【分析】分别求解函数的定义域和值域化简集合A，B，然后取交集得答案．【解答】解：A={x|y=x﹣1}，∴A=R，由y=x2﹣1≥﹣1，得B={y|y=x2﹣1}=[﹣1，+∞），则A∩B=[﹣1，+∞），故选：C．【点评】本题考查交集及其运算，考查了函数的定义域和值域的求法，是基础题．2．已知=（5，6），=（sinα，cosα），已知向量且∥，则tanα=（）A．B．﹣C．D．﹣【考点】平面向量共线（平行）的坐标表示．【专题】平面向量及应用．【分析】根据两个向量平行的坐标表示，直接代入公式求解即可．【解答】解： =（5，6），=（sinα，cosα），∥，∴5cosα=6sinα，∴tanα=，故选：A．【点评】本题考查了两个向量平行的坐标表示，平行问题是一个重要的知识点，在高考题中常常出现，常与向量的模、向量的坐标表示等联系在一起，要特别注意垂直与平行的区别．3．若复数z满足（z+1）i=2﹣i，则复数z的共轭复数在复平面上所对应点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】复数代数形式的乘除运算；复数的代数表示法及其几何意义．【专题】数系的扩充和复数．【分析】由（z+1）i=2﹣i，利用复数代数形式的乘除运算求出z，则z的共轭复数可求，进一步求出复数z的共轭复数在复平面上所对应点的坐标，则答案可求．【解答】解：∵（z+1）i=2﹣i，∴．则．∴复数z的共轭复数在复平面上所对应点的坐标为：（﹣2，2），位于第二象限．故选：B．【点评】本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．4．从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，这个点在圆x2+y2=2016内部的概率是（）A．B．C．D．【考点】列举法计算基本事件数及事件发生的概率．【专题】概率与统计．【分析】从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，基本事件总数n=5，再用列举法求出这个点在圆x2+y2=2016内部，包含的基本事件个数，由此利用等可能事件概率计算公式能求出这个点在圆x2+y2=2016内部的概率．【解答】解：从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，基本事件总数n=5，这个点在圆x2+y2=2016内部，包含的基本事件有：（20，30），（10，10），共2个，∴这个点在圆x2+y2=2016内部的概率p=．故选：B．【点评】本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．5．已知双曲线的渐近线方程为y=±x，且经过点（4，1），则双曲线的标准方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1【考点】双曲线的简单性质．【专题】计算题；圆锥曲线的定义、性质与方程．【分析】设双曲线方程为y2﹣x2=λ，代入点（4，1），求出λ，即可求出双曲线的标准方程．【解答】解：设双曲线方程为y2﹣x2=λ，代入点（4，1），可得1﹣=λ，∴λ=﹣3，∴双曲线的标准方程是=1．故选：C．【点评】本题考查双曲线的标准方程，考查学生的计算能力，正确设出双曲线的方程是关键．6．各顶点都在一个球面上的正四棱柱的高是2，体积是16，则这个球的表面积是（）A．16π B．20π C．24π D．32π【考点】球的体积和表面积．【专题】空间位置关系与距离．【分析】先求出正四棱柱的底面边长，再求其对角线的长，就是外接球的直径，然后求出球的表面积．【解答】解：各顶点都在一个球面上的正四棱柱高为2，体积为16，它的底面边长是：2，所以它的体对角线的长是：2，球的直径是：2，所以这个球的表面积是：4π（）2=20π故选：B．【点评】本题考查正四棱柱的外接球的表面积．考查计算能力，是基础题7．设等差数列{a n}的公差是d，其前项和是S n，若a1=d=1，则的最小值是（）A．B．C．2+D．2﹣【考点】等差数列的性质．【专题】等差数列与等比数列．【分析】利用等差数列的通项公式及其前n项和公式可得：a n=n，S n=，于是=，再利用基本不等式的性质即可得出．【解答】解：a n=1+（n﹣1）=n，S n=，∴===，当且仅当n=4时取等号．∴的最小值是．故选：A．【点评】本题考查了等差数列的通项公式及其前n项和公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．8．已知a，b∈R+，函数f（x）=alog2x+b的图象经过点（4，1），则+的最小值为（）A．6﹣2B．6 C．4+2D．8【考点】基本不等式在最值问题中的应用．【专题】不等式的解法及应用．【分析】利用函数的图象经过的点，得到a、b关系式，然后求出最值．【解答】解：a，b∈R+，函数f（x）=alog2x+b的图象经过点（4，1），可得2a+b=1，则+=（+）（2a+b）=2+2+≥=8，当且仅当b=2a=时取等号，表达式的最小值为8．故选：D．【点评】本题考查基本不等式在最值中的应用，考查计算能力．9．对一名学生数学成绩统计了8次，第i次统计得到的数据为a i，具体如下表所示：在对上述统计数据的分析中，一部分计算见如图所示的算法流程图（其中是这8个数据的平均数），则输出的S的值是（）A．9 B．8 C．7 D．6【考点】程序框图．【专题】计算题；算法和程序框图．【分析】由题意及程序框图知，该程序框图的功能是输出这8个数据的方差，由公式结合题设中的数据计算出方差，选出正确选项．【解答】解：该程序框图的功能是输出这8个数据的方差，因为这8个数据的平均数==104，故其方差 [（100﹣104）2+（101﹣104）2+（103﹣104）2+（103﹣104）2+（104﹣104）2+（106﹣104）2+（107﹣104）2+（108﹣104）2]=7，输出的S的值为7．故选C【点评】本题考查循环结构，理解题意，由框图得出本题所研究问题的算法是解题的关键．10．对任意的实数x都有f（x+2）﹣f（x）=2f（1），若y=f（x﹣1）的图象关于x=1对称，且f（0）=2，则f（2015）+f（2016）=（）A．0 B．2 C．3 D．4【考点】抽象函数及其应用．【专题】函数的性质及应用．【分析】根据条件判断函数f（x）是偶函数，结合条件关系求出函数的周期，进行转化计算即可．【解答】解：y=f（x﹣1）的图象关于x=1对称，则函数y=f（x）的图象关于x=0对称，即函数f（x）是偶函数，令x=﹣1，则f（﹣1+2）﹣f（﹣1）=2f（1），即f（1）﹣f（1）=2f（1）=0，即f（1）=0，则f（x+2）﹣f（x）=2f（1）=0，即f（x+2）=f（x），则函数的周期是2，又f（0）=2，则f（2015）+f（2016）=f（1）+f（0）=0+2=2，故选：B．【点评】本题主要考查函数值的计算，根据抽象函数关系判断函数的周期性和奇偶性是解决本题的关键．11．一个几何体的正视图和俯视图如图所示，其中俯视图是边长为2的正三角形及其内切圆，则侧视图的面积为（）A．6+π B． C．6+4πD．【考点】由三视图求面积、体积．【专题】计算题；空间位置关系与距离．【分析】几何体是三棱柱与球的组合体，判断三棱柱的高及底面三角形的边长，计算球的半径，根据侧视图是矩形上边加一个圆，分别计算矩形与圆的面积再相加．【解答】解：由三视图知：几何体是三棱柱与球的组合体，其中三棱柱的高为2，底面三角形的边长为2，根据俯视图是一个圆内切于一个正三角形，球的半径R==1，几何体的侧视图是矩形上边加一个圆，矩形的长、宽分别为2，3，圆的半径为1，侧视图的面积S=2×3+π×12=6+π．故选：A．【点评】本题考查了由正视图与俯视图求侧视图的面积，判断数据所对应的几何量及求得相关几何量的数据是解题的关键．12．函数f（x）=，若方程f（x）=﹣x+a有且只有两个不等的实数根，则实数a的取值范围为（）A．（﹣∞，0）B．[0，1）C．（﹣∞，1）D．[0，+∞）【考点】根的存在性及根的个数判断．【专题】数形结合；函数的性质及应用．【分析】由题知f（x）为分段函数，当x＜0时，由f（x）=f（x+1）可知f（x）为周期函数；当x大于等于0时函数为增函数，而方程f（x）=﹣x+a有且只有两个不相等的实数根即f（x）与y=﹣x+a由两个交点，在同一坐标系中画出函数f（x）的图象与函数y=﹣x+a 的图象，利用数形结合，易求出满足条件实数a的取值范围．【解答】解：函数f（x）=的图象如图所示，作出直线l：y=a﹣x，向左平移直线l观察可得函数y=f（x）的图象与函数y=﹣x+a的图象有两个交点，即方程f（x）=﹣x+a有且只有两个不相等的实数根，即有a＜1，故选：C．【点评】本题考查学生综合运用函数和方程的能力，以及让学生掌握数形结合的数学思想．二、填空题（本大题共4小题，每小题5分，共20分）13．函数f（x）=xe x的图象在x=1处的切线方程为2ex﹣y﹣e=0 ．【考点】利用导数研究曲线上某点切线方程．【专题】导数的综合应用．【分析】先求出切点的坐标，然后求出x=1处的导数，从而求出切线的斜率，利用点斜式方程即可求出切线方程．【解答】解：∵f（x）=xe x，∴f′（x）=e x+xe x，∴f′（1）=2e，又f（1）=e，∴曲线y=f（x）在点（1，f（1））处的切线方程为y﹣e=2e（x﹣1），即2ex﹣y﹣e=0．【点评】本题主要考查了利用导数研究曲线上某点切线方程，考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，正确求导和运用点斜式方程是解题的关键，属于中档题．14．若x，y满足约束条件，则z=2x+y的最大值为12 ．【考点】简单线性规划．【专题】不等式的解法及应用．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，求最大值．【解答】解：作出不等式组对应的平面区域如图：（阴影部分）．由z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最大，此时z最大．由，解得，即A（3，6），代入目标函数z=2x+y得z=2×3+6=6+6=12．即目标函数z=2x+y的最大值为12．故答案为：12．【点评】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．15．已知抛物线y2=﹣2px（p＞0）的准线与圆（x﹣5）2+y2=25相切，则p的值为20 ．【考点】抛物线的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】由题意可得圆心（5，0）到直线x=的距离等于半径5，即|5﹣|=5，由此求得p的值．【解答】解：∵抛物线y2=﹣2px（p＞0）的准线x=与圆（x﹣5）2+y2=25相切，∴圆心（5，0）到直线x=的距离等于半径5，即|5﹣|=5，求得p=20 或p=0（舍去），故答案为：20．【点评】本题主要考查抛物线的标准方程和简单性质，直线和圆的位置关系，属于基础题．16．函数f（x）=sinx﹣acosx的图象的一条对称轴是x=，则g（x）=asinx+cosx=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤）的初相是．【考点】三角函数中的恒等变换应用；y=Asin（ωx+φ）中参数的物理意义．【专题】函数思想；综合法；三角函数的图像与性质．【分析】化简得f（x）=sin（x﹣θ），由对称轴得f（）=±求出a，代入g（x）化简可得答案．【解答】解：f（x）=sinx﹣acosx=sin（x﹣θ），（θ为辅助角），∵x=是f（x）的一条对称轴，∴sin﹣acos=±，即﹣﹣=±，化简得a2﹣2a+1=0，解得a=1，∴g（x）=sinx+cosx=sin（x+），∴g（x）的初相为．故答案为：．【点评】本题考查函数的对称性，考查辅助角公式和两角和差的正弦及余弦公式的运用，考查运算能力，属于基础题和易错题．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．在△ABC中，角A、B、C的对边分别为a、b、c．已知a+b=5，c=，且．（1）求角C的大小；（2）求△ABC的面积．【考点】解三角形；二倍角的余弦；余弦定理．【专题】计算题．【分析】（1）由三角形的内角和定理及诱导公式化简已知的等式，再根据二倍角的余弦函数公式化简，合并整理后得到关于cosC的方程，求出方程的解得到cosC的值，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数；（2）利用余弦定理表示出c2=a2+b2﹣2abcosC，再根据完全平方公式变形后，将a+b，c及cosC的值代入求出ab的值，然后再由ab，sinC的值，利用三角形的面积公式即可求出三角形ABC的面积．【解答】解：（1）∵A+B+C=180°，∴=90°﹣，由得：，∴，整理得：4cos2C﹣4cosC+1=0，解得：，∵0°＜C＜180°，∴C=60°；（2）由余弦定理得：c2=a2+b2﹣2abcosC，即7=a2+b2﹣ab，∴7=（a+b）2﹣3ab=25﹣3ab⇔ab=6，∴．【点评】此题属于解三角形的题型，涉及的知识有：诱导公式，二倍角的余弦函数公式，余弦定理，三角形的面积公式，以及完全平方公式的运用，熟练掌握公式及定理是解本题的关键．18．已知在四棱锥S﹣ABCD中，四边形ABCD是菱形，SD⊥平面ABCD，P为SB的中点，Q为BD上一动点．AD=2，SD=2，∠DAB=．（Ⅰ）求证：AC⊥PQ；（Ⅱ）当PQ∥平面SAC时，求四棱锥P﹣AQCD的体积．【考点】棱柱、棱锥、棱台的体积；空间中直线与直线之间的位置关系．【专题】综合题；转化思想；综合法；立体几何．【分析】（Ⅰ）证明AC⊥平面SBD，即可证明：AC⊥PQ；（Ⅱ）当PQ∥平面SAC时，设AC∩BD=O，取BO的中点Q，即可求四棱锥P﹣AQCD的体积．【解答】（Ⅰ）证明：∵四边形ABCD是菱形，∴AC⊥BD，∵SD⊥平面ABCD，∴SD⊥AC，∵BD∩SD=D，∴AC⊥平面SBD，∵PQ⊂平面SBD，∴AC⊥PQ；（Ⅱ）解：设AC∩BD=O，取BO的中点Q，∴PQ∥SO，∵SO⊂平面SAC，PQ⊄平面SAC，∴PQ∥平面SAC，连接PO，则PO∥SD，且PO=SD=1，PO⊥平面ABCD，∵S四边形AQCD=S菱形ABCD=，∴V四棱锥P﹣AQCD=S四边形AQCD═．【点评】本题考查线面垂直的判定与性质，考查四棱锥P ﹣AQCD 的体积，考查学生分析解决问题的能力，属于中档题．19．（Ⅰ）如表所示是某市最近5年个人年平均收入表节选．求y 关于x 的回归直线方程，并估计第6年此市的个人年平均收入（保留三位有效数字）．其中x i y i =421，x i 2=55附1： =， =﹣（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表：完成上表，并回答：是否有95%以上的把握认为“收入与接受培训时间有关系”．附2：附3： K 2=．（n=a+b+c+d ）【考点】独立性检验的应用． 【专题】概率与统计．【分析】（1）根据已知数据求出回归直线方程，将x=6代入，可估计第6年此市的个人年平均收入；（2）通过所给的数据计算K 2观测值，同临界值表中的数据进行比较，可得到结论． 【解答】解：（1）由已知中数据可得： =3， =26.4， ∵x i y i =421，x i 2=55，∴====2.5，=﹣=26.4﹣7.5=18.9，∴=2.5x+18.9， 当x=6时， =33.9．即第6年此市的个人年平均收入约为33.9千元；（2）某行业个人平均收入与接受专业培训时间关系得到2×2列联表：根据列联表中的数据，得到K 2的观测值为 K 2=≈4.762＞3.841．故我们有95%的把握认为“收入与接受培训时间有关系”．【点评】本题考查的知识是回归分析和独立性检验，计算量较大，属于中档题．20．已知椭圆C 满足：过椭圆C 的右焦点F （，0）且经过短轴端点的直线的倾斜角为．（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为坐标原点，若点A 在直线y=2上，点B 在椭圆C 上，且OA⊥OB，求线段AB 长度的最小值．【考点】椭圆的简单性质．【专题】方程思想；待定系数法；圆锥曲线的定义、性质与方程．【分析】（Ⅰ）设椭圆方程为+=1（a＞b＞0），运用直线的斜率公式，求出a，b，即可求椭圆C的方程；（Ⅱ）先表示出线段AB长度，再利用基本不等式，求出最小值．【解答】解：（Ⅰ）设椭圆方程为+=1（a＞b＞0），由题意可得c=，设短轴的端点为（0，﹣b），可得=tan=1，解得b=，∴a==2，∴椭圆方程为+=1；（Ⅱ）设A（t，2），B（x0，y0），x0≠0，则∵OA⊥OB，∴•=0，∴tx0+2y0=0，∴t=﹣，∵x02+2y02=4，∴|AB|2=（x0﹣t）2+（y0﹣2）2=（x0+）2+（y0﹣2）2=x02+y02++4=x02+++4=++4（0＜x02≤4），因为+≥4（0＜x02≤4），当且仅当=，即x02=4时等号成立，所以|AB|2≥8．∴线段AB长度的最小值为2．【点评】本题考查椭圆的方程与性质，考查基本不等式的运用，考查学生的计算能力，属于中档题．21．己知函数f（x）=（a+1）lnx+x﹣，其中a∈R．（I）求f（x）的单调区间；（Ⅱ）若在[1，e]上存在x0，使得f（x0）＜0成立，求a的取值范围．【考点】利用导数研究函数的单调性；函数恒成立问题．【专题】导数的综合应用．【分析】（Ⅰ）先求出函数的单调区间，通过讨论a的范围，确定函数的单调性；（Ⅱ）通过讨论a的范围，得到f（x）在[1，e]的单调性，求出[1，e]的最小值即可求出a的范围．【解答】解：（Ⅰ）函数f（x）的定义域是（0，+∞），f′（x）=+1+=，①a≥0时，f′（x）＞0在（0，+∞）恒成立，∴f（x）在（0，+∞）递增；②a＜0时，令f′（x）＞0，解得：x＞﹣a，令f′（x）＜0，解得：x＜﹣a，∴f（x）在（0，﹣a）递减，在（﹣a，+∞）递增；（Ⅱ）①由（Ⅰ）得：﹣a≤1即a≥﹣1时：f（x）在[1，e]递增，若在[1，e]上存在x0，使得f（x0）＜0成立，只需f（1）=1﹣a＜0即可，解得：a＞1；②若1＜﹣a＜e即﹣e＜a＜﹣1时：f（x）在[1，﹣a）递减，在（﹣a，e]递增，若在[1，e]上存在x0，使得f（x0）＜0成立，只需f（﹣a）＜0即可，即（a+1）ln（﹣a）+（﹣a）+1＜0，即ln（﹣a）＞1﹣，而1＜﹣a＜e，则0＜ln（﹣a）＜1，1﹣＞1，∴ln（﹣a）＞1﹣，无解；③若﹣a≥e，即a≤﹣e时：f（x）在[1，e]递减，若在[1，e]上存在x0，使得f（x0）＜0成立，只需f（e）＜0即可，即（a+1）+e﹣＜0，解得：a＜﹣；综上：a＞1或a＜﹣．【点评】本题考查了函数的单调性、最值问题，考查导数的应用，分类讨论思想，是一道中档题．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一个计分.【选修4-1几何证明选讲】22．如图，过圆外一点P的直线交圆O于A、B两点，PE是圆O的切线，CP平分∠APE，分别与AE、BE交于点C，D．求证：（1）CE=DE；（2）=．【考点】相似三角形的判定．【专题】证明题；数形结合；综合法；推理和证明．【分析】（1）由弦切角定理得∠A=∠BEP，由角平分线性质得到∠ECD=∠EDC，由此能证明EC=ED．（2）由已知条件推导出△PBD∽△PEC，△PDE∽△PCA，由此能证明=．【解答】证明：（1）∵PE是圆O的切线，∴∠A=∠BEP，∵PC平分∠APE，∴∠A+∠CPA=∠BEP+∠DPE，∵∠ECD=∠A+∠CPA，∠EDC=∠BEP+∠DPE，∴∠ECD=∠EDC，∴EC=ED．（2）∵∠PDB=∠EDC，∠EDC=∠ECD，∠PDB=∠PCE，∴∠BPD=∠EPC，∴△PBD∽△PEC，∴，同理，△PDE∽△PCA，∴，∴=．【点评】本题考查两条线段相等的证明，考查线段比值相等的证明，是基础题，解题时要认真审题，注意弦切角定理和三角形相似的性质定理的合理运用．【选修4─4：坐标系与参数方程选讲】23．设平面直角坐标系原点与极坐标极点重合，x轴正半轴与极轴重合，若已知曲线C的极坐标方程为ρ2=，点F1、F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．（Ⅰ）求曲线C的标准方程和直线l的普通方程；（Ⅱ）若点P为曲线C上的动点，求点P到直线l的最大距离．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【专题】方程思想；转化思想；坐标系和参数方程．【分析】（I）利用即可把曲线C的极坐标方程化为直角坐标方程；消去参数即可得到直线l的普通方程．（II）设P，θ∈[0，2π），则点P到直线l的距离d==，再利用三角函数的单调性即可得出．【解答】解：（I）曲线C的极坐标方程为ρ2=，化为直角坐标方程：3x2+4y2=12，即=1．直线l 的参数方程为（t 为参数，t ∈R ），化为普通方程：x ﹣1﹣y=0．（II ）设P，θ∈[0，2π），则点P 到直线l 的距离d==≤=，其中α=arctan ．∴点P 到直线l 的最大距离是．【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式、三角函数的单调性，考查了推理能力与计算能力，属于中档题．．【选修4-5：不等式选讲】24．设函数f （x ）=|2x ﹣1|，x ∈R ．（Ⅰ）求不等式|f （x ）﹣2|≤5的解集；（Ⅱ）若g （x ）=的定义域为R ，求实数m 的取值范围．【考点】绝对值不等式的解法；函数的定义域及其求法．【专题】三角函数的图像与性质．【分析】（Ⅰ）不等式|f （x ）﹣2|≤5，即|2x ﹣1|≤7，即﹣7≤2x﹣1≤7，由此求得不等式的解集．（Ⅱ）由题意可得f （x ）+f （x ﹣1）+m≠0 恒成立，即|x ﹣|+|x ﹣|≠﹣恒成立．根据绝对值的意义求得|x ﹣|+|x ﹣|的最小值为1，可得﹣＜1，由此求得m 的范围．【解答】解：（Ⅰ）不等式|f （x ）﹣2|≤5，即﹣5≤f（x ）﹣2≤5，即﹣3≤f（x ）≤7，即|2x ﹣1|≤7，即﹣7≤2x﹣1≤7，求得﹣3≤x≤4，故不等式的解集为{x|﹣3≤x≤4}．（Ⅱ）若g （x ）=的定义域为R ，则f （x ）+f （x ﹣1）+m≠0 恒成立，即|2x ﹣1|+|2（x ﹣1）﹣1|≠﹣m ，即|x ﹣|+|x ﹣|≠﹣恒成立．根据绝对值的意义，|x﹣|+|x﹣|表示数轴上的x对应点到、对应点的距离之和，它的最小值为1，故﹣＜1，求得m＞﹣2．【点评】本题主要考查绝对值的意义，绝对值不等式的解法，函数的恒成立问题，体现了转化的数学思想，属于中档题．。

12016届高三年级第二次四校联考数学（理）试题2015.12命题：康杰中学 临汾一中 忻州一中 长治二中【满分150分，考试时间为120分钟】一、选择题(5×12＝60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号)1．已知集合{}|1M x x =>，集合{}2|20N x x x =-<，则M N I 等于 A ．{}|12x x << B ．{}|01x x << C ． {}|02x x <<D ．{}|2x x >2．i 是虚数单位，若21ia bi i+=++(,)a b R ∈，则lg()a b +的值是 A ．2-B ．1-C ．0D ．123. 阅读右边的程序框图，运行相应的程序．若输入x 的值为1，则输出S 的值为A. 64B. 73C. 512D. 5854. 已知等比数列{}n a 中，各项都是正数，且1321,,22a a a 成等差数列，则91078a aa a +=+A. 1+B. 1-3+D.3-5. 已知|a |＝1，|b r |＝2，且()a a b ⊥-r r，则向量a r 与向量b r 的夹角为A.6π B. 4π C.3πD.23π6. 某学校组织学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[)[)20,40,40,60[)[)60,80,80,100,若低于60分的人数是15人,则该班的学生人数是2A ．45B ．50C ．55D ．607. "0"a ≤是“函数()=(-1)f x ax x 在区间(0,+)∞内单调递增”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件8. 某三棱锥的三视图如图所示,该三棱锥的表面积是A．28+ B．60+ C．56+D ．30+9.将函数()sin y x x x R =+∈的图像向左平移()0m m >个 单位长度后,所得到的图像关于y 轴对称,则m 的最小值是A. 6π B.12πC. 3πD.56π10. 已知()()()()10210012101111x a a x a x a x +=+-+-++-L ，则8a 等于A ．－5B ．5C ．90D ．18011. 设抛物线2:3(0)C y px p =>的焦点为F ，点M 在C 上， 5MF =，若以MF 为直径的圆过点(0,2)，则C 的方程为A ．2248y x y x==或 B ．2228y x y x ==或C ．22416y x y x ==或D ．22216y x y x ==或 12. 已知函数21()(0)2xf x x e x =+-<与()()2ln g x x x a =++的图象上存在关于y 轴对称的点，则a 的取值范围是A．⎛-∞ ⎝ B．(-∞ C．⎛ ⎝ D．⎛⎝二、填空题:（本大题共4小题，每小题5分，共20分。

2016届高三年级第一次四校联考文科数学试题命题： 忻州一中 康杰中学 临汾一中 长治二中(考试时间120分钟 满分150分)一、选择题(5×12＝60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号. ) 1. 已知集合}{{}211A x y x B y y x ==-==-，，则B A = A ．∅B ．{}(0,1),(1,0)-C ．[)1,-+∞D ．{}0,12. 已知(5,6)(sin ,cos )a b αα==，，已知向量且//a b ，则tan α=A ．65B ．65-C ．56D ．56-3. 若复数z 满足(1)2z i i +=-，则复数z 的共轭复数在复平面上所对应点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限4. 从(40,30)， (50,10)， (20,30) ， (45,5) ， (10,10)这5个点中任取一个点，这个点在圆222016x y +=内部的概率是A ．53B ．52 C ．51 D ．545. 已知双曲线的渐近线方程为x y 21±=，且经过点(4,1)，则双曲线的标准方程是A ．112322=-y x B ．112322=-x y C ．131222=-y x D ．131222=-x y 6. 各顶点都在一个球面上的正四棱柱的高是2，体积是16，则这个球的表面积是 A ．π16 B ．π20 C ．π24 D ．π327. 设等差数列{}n a 的公差是d ，其前项和是n S ，若11==d a ，则8n nS a +的最小值是 A ．29B ．27C ．2122+D ．2122- 8. 已知,a b R +∈，函数2()log f x a x b =+的图像经过点(4,1)，则12a b+的最小值为A．6- B ．6 C．4+D ．8 9. 对一名学生数学成绩统计了8次，第i 次统计得到的数据为i a ，具体如下表所示：在对上述统计数据的分析中，一部分计算见如图所示的算法流程图 (其中a 是这8个数据的平均数)，则输出的S 的值是A ．9B ．8C ． 7D ．610. 对任意的实数x 都有(2)()2(1),f x f x f +-=若(1)y f x =-的图像 关于1x =对称，且(0)2,f =则(2015)(2016)f f +=A ．0B ．2C ． 3D ．4 11. 一个几何体的正视图和俯视图如图所示，其中俯视图是边长为2 3的正三角形，且圆与三角形内切，则侧视图的面积为A ．6＋πB ．43＋πC ．6＋4πD ．43＋4π12. 函数21(0)()(1)(0)x x f x f x x ⎧-≥=⎨+<⎩若方程a x x f +-=)(有且只有两个不等的实数根，则实数a的取值范围为 A ．(-∞,0)B ．[0,1)C ．(-∞,1)D ．[0,+∞)二、填空题（本大题共4小题，每小题5分，共20分）13. 函数()x f x xe =的图象在1x =处的切线方程为 ▲ .14. 若,x y 满足约束条件22030,3x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩则2z x y =+的最大值为 ▲ .15. 已知抛物线22(0)y px p =->的准线与圆22(5)25x y -+=相切，则p 的值为 ▲ .16. 函数()x f =x a x cos sin 3- 的图象的一条对称轴是35π=x ，则 ()sin cos sin()(0,0,)2g x a x x A x A πωϕωϕ=+=+>>≤的初相是 ▲ .三、解答题(本大题共8小题，共70分. 解答应写出文字说明、证明过程或演算步骤. ) 17. (本小题满分12分)在△ABC 中，A 、B 、C 的对边分别为a 、b 、c ，已知a ＝7，b ＋c ＝5，且4sin 2 B ＋C 2－cos2A ＝72.(Ⅰ)求角A 的大小； (Ⅱ)求△ABC 的面积． 18. (本小题满分12分)已知在四棱锥ABCD S -中，四边形ABCD 是菱形，SD ⊥平面ABCD ,P 为SB的中点，Q 为BD 上一动点.2,2,.3AD SD DAB π==∠=(Ⅰ)求证：PQ AC ⊥；(Ⅱ)当PQ //平面SAC 时，求四棱锥AQCD P -的体积. 19. (本小题满分12分)(Ⅰ)如图所示是某市最近5年个人年平均收入表节选. 求y 关于x 的回归直线方程，并估计第6年此市的个人年平均收入（保留三位有效数字）.（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到22⨯列联表：完成上表，并回答：是否有%95以上的把握认为“收入与接受培训时间有关系”．附2：20. (本小题满分12分)0k0.4550.7082.7063.8416.635已知椭圆C 满足：过椭圆C的右焦点F 且经过短轴端点的直线的倾斜角为4π.（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为坐标原点，若点A 在直线2y =上，点B 在椭圆C 上，且OA OB ⊥，求线段AB 长度的最小值. 21. (本小题满分12分)已知函数()(1)ln ,af x a x x x=++-其中.a R ∈ （Ⅰ）求()f x 的单调区间；（Ⅱ）若在[]1,e 上存在0x ，使得0()0f x <成立，求a 的取值范围.请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一个计分. 22. (本小题满分10分)选修4—1几何证明选讲如图，过圆外一点P 的直线交圆O 于A 、B 两点，PE 是圆O 的切线，CP 平分 ∠APE ，分别与AE 、BE 交于点D C ,. 求证：（Ⅰ） DE CE =； （Ⅱ）.CA PECE PB= 23. (本小题满分10分)选修4─4：坐标系与参数方程选讲 设平面直角坐标系原点与极坐标极点重合，x 轴正半轴与极轴重合，若已知曲线C 的极坐标方程为222123cos 4sin ρθθ=+，点F 1、F 2为其左、右焦点，直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+=t y t x 22221(t 为参数，R t ∈).（Ⅰ）求曲线C 的标准方程和直线l 的普通方程；（Ⅱ）若点P 为曲线C 上的动点，求点P 到直线l 的最大距离. 24. (本小题满分10分)选修4—5：不等式选讲(Ⅱ)若1()()(1)g x f x f x m=+-+的定义域为R ，求实数m 的取值范围.。

2016届高三年级第一次四校联考政治试题答案①选择题：1—5CBDCC 6—10ABCDC 11—15BDBCC 16—20BBAAC 21—24BAAC25.（8分）①收入是消费的基础和前提。

进一步释放我国居民的信息消费潜力，必须保持经济的稳定增长，增加居民收入。

②收入差距是影响社会总体消费水平的重要因素。

应该促进城乡协调发展，缩小收入差距，提高我国居民的总体信息消费水平。

③生产决定消费。

要丰富文化产品供给，满足人们多样化的信息消费需求。

④消费观念影响消费行为，消费者要转变消费观，注重协调消费，增加对信息产品的消费。

（每点2分）26.（10分）①价值规律促使商品生产者提高劳动生产率，降低生产成本。

创客的一大优势就在于以更低的成本，创造出更多的适销对路的高质量产品。

（2分）②普通大众作为市场经济活动的参加者，成为平等的创新者，得益于大众创业、万众创新的良好市场环境。

（2）③创客面向市场，推出新产品满足多样化市场需求，发挥了市场在资源配置中的决定性作用。

（3分）④从创客发起地看，市场体制健全，市场秩序规范，市场体系完善，是创客之燎原的重要土壤。

(3分)27.（8分）参考答案：中国共产党要坚持全心全意为人民服务的宗旨；坚持以人为本、执政为民的执政理念；坚持科学执政、民主执政、依法执政，重视扶贫开发工作，为扶贫开发工作制定科学的方针、政策；在扶贫开发工作中发挥总揽全局、协调各方的领导核心作用。

（每点2分）28.（1）（8分）①N市政府关心民生、服务于民，做到了权为民所用、情为民所系、利为民所谋。

（或政府宗旨及工作原则）（2分）②N市政府通过及时公开政府信息，自觉接受人民监督权，以提高政府工作的透明度和工作效率，做到审慎用权、依法决策、科学决策和民主决策。

（2分）③N市政府通过深化体制改革，转变政府职能来提高政府依法行政和服务经济社会发展的能力和水平，提高政府工作人员的业绩。

（2分）④N市政府通过加大政府在宏观调控、市场监管等方面的责任，履行其组织社会主义经济建设的职能，维护了广大人民群众的根本利益。

山西省康杰中学、临汾一中、忻州一中、长治二中2016届上学期第二次联考文数试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.已知}{0322≤--=x x x A ，{}32+==x y y B ，则=⋂B A （ ）A.⎡⎣B.C. ⎤⎦D. ⎡⎣2.若复数z 满足12)1(-=+i i z ，则复数z 的虚部为（ ） A.1- B. 0 C. i D. 1 3.已知平面向量a ，b 满足()3a a b ⋅+=，且2a =，1b =，则向量a 与b 夹角的正弦值为（ ）A. 12-B.C. 12D.4.甲乙两人有三个不同的学习小组A ，B ，C 可以参加，若每人必须参加并且仅能参加一个学习小组，则两人参加同一个小组的概率为（ ） A.31 B. 41 C. 51 D. 165.执行如图所示的程序框图，若输出的结果为3，则可输入的实数x 值的个数为（ ）A. 1B.2 C.3 D. 46.已知双曲线1:2222=-by a x C )0,0(>>b a ，右焦点F 到渐近线的距离为2，F 到原点的距离为3，则双曲线C 的离心率e 为（ ）A.35 B. 553 C. 36 D. 26 7.某三棱锥的三视图如图所示，该三棱锥的表面积是 （ ）A ．28＋6 5B ．30＋6 5C ．56＋12 5D ．60＋12 58.已知数列2008，2009，1，－2008，…这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2014项之和2014S 等于（ ） A ．1B ．4 018C ．2 010D ．09.已知三棱锥ABC P -，在底面ABC ∆中，060A ∠=，BC =，ABC PA 面⊥，2=PA ，则此三棱锥的外接球的体积为（ ）A B. C.D. 8π 10.已知函数()f x 满足：①定义域为R ；②x R ∀∈，都有)()2(x f x f =+；③当[1,1]x ∈-时，()||1f x x =-+，则方程x x f 2log 21)(=在区间[3,5]-内解的个数是（ ） A ．5B ．6C ．7D ．811.已知函数()()sin 2f x x φ=+ (其中φ是实数)，若()()6f x f π≤对x R ∈恒成立，且()(0)2f f π>，则()f x 的单调递增区间是（ ）A. ,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ B. ,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C. 2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D. ,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦12.函数32231(0)()(0),ax x x x f x e x ⎧++≤⎪=⎨>⎪⎩在[]2,3-上的最大值为2，则实数a 的取值范围是（ ）A. 1[ln 2,)3+∞B. 1[0,ln 2]3C. (,0]-∞D. 1(,ln 2]3-∞二、填空题（每题4分，满分20分，将答案填在答题纸上）13.已知()ln 1,(0,)f x ax x x =+∈+∞（a R ∈），()f x '为()f x 的导函数，(1)2f '=，则a =14.若,x y 满足约束条件20210220x y x y x y +-≤⎧⎪-+≤⎨⎪-+≥⎩，则3z x y =+的最大值为15.抛物线22(0)x py p =>的焦点为F ，其准线与双曲线221x y -=相交于,A B 两点，若△ABF 为等边三角形，则p ＝16.在ABC ∆中，角C B A 、、所对的边分别为c b a 、、，且c A b B a 21cos cos =-，当)tan(B A -取最大值时，角B 的值为三、解答题 （本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）已知等比数列{}n a 的各项均为正数， 11a =，公比为q ；等差数列{}n b 中，13b =，且{}n b 的前n 项和为n S ，233227,S a S q a +==. （Ⅰ）求{}n a 与{}n b 的通项公式； （Ⅱ）设数列{}n c 满足32n nc S =，求{}n c 的前n 项和n T . 18.（本小题满分12分）如图，在直三棱柱111C B A ABC -中，底面是正三角形，点D 是11B A 中点，2AC =，21=CC ．（Ⅰ）求三棱锥1BDC C -的体积; （Ⅱ）证明：11BC C A ⊥.19.（本小题满分12分）某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：为了研究计算的方便，工作人员将上表的数据进行了处理，2010,5t x z y =-=-得到下表2：（Ⅰ）求z 关于t 的线性回归方程；（Ⅱ）通过（Ⅰ）中的方程，求出y 关于x 的回归方程；（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？（附：对于线性回归方程ˆˆˆybx a =+，其中1221ˆˆˆ,ni ii nii x y nx yb ay bx xnx ==-⋅==--∑∑）20.（本小题满分12分）如图，圆C 与x 轴相切于点)0,2(T ，与y 轴正半轴相交于两点,M N （点M 在点N 的下方），且3MN =． （Ⅰ）求圆C 的方程；（Ⅱ）过点M 任作一条直线与椭圆22184x y +=相交于两点A B 、，连接AN BN 、，求证：ANM BNM ∠=∠．21.（本小题满分12分） 已知函数1()ln f x a x x=-（a R ∈）. （Ⅰ）若()()2h x f x x =-，当3a =-时，求()h x 的单调递减区间； （Ⅱ）若函数()f x 有唯一的零点，求实数a 的取值范围.选做题：请考生从第22、23、24三题中任选一题作答。

2015-2016学年山西省忻州一中、长治二中、康杰中学、临汾一中高三（上）第一次联考数学试卷（文科）参考答案与试题解析一、选择题（60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B铅笔涂黑答题纸上对应题目的答案标号.）1．已知集合A={x|y=x﹣1}，B={y|y=x2﹣1}，则A∩B=（）A．∅B．{（0，﹣1），（1，0）} C．[﹣1，+∞）D．{0，1}【考点】交集及其运算．【专题】集合．【分析】分别求解函数的定义域和值域化简集合A，B，然后取交集得答案．【解答】解：A={x|y=x﹣1}，∴A=R，由y=x2﹣1≥﹣1，得B={y|y=x2﹣1}=[﹣1，+∞），则A∩B=[﹣1，+∞），故选：C．【点评】本题考查交集及其运算，考查了函数的定义域和值域的求法，是基础题．2．已知=（5，6），=（sinα，cosα），已知向量且∥，则tanα=（）A． B．﹣C． D．﹣【考点】平面向量共线（平行）的坐标表示．【专题】平面向量及应用．【分析】根据两个向量平行的坐标表示，直接代入公式求解即可．【解答】解：=（5，6），=（sinα，cosα），∥，∴5cosα=6sinα，∴tanα=，故选：A．【点评】本题考查了两个向量平行的坐标表示，平行问题是一个重要的知识点，在高考题中常常出现，常与向量的模、向量的坐标表示等联系在一起，要特别注意垂直与平行的区别．3．若复数z满足（z+1）i=2﹣i，则复数z的共轭复数在复平面上所对应点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】复数代数形式的乘除运算；复数的代数表示法及其几何意义．【专题】数系的扩充和复数．【分析】由（z+1）i=2﹣i，利用复数代数形式的乘除运算求出z，则z的共轭复数可求，进一步求出复数z的共轭复数在复平面上所对应点的坐标，则答案可求．【解答】解：∵（z+1）i=2﹣i，∴．则．∴复数z的共轭复数在复平面上所对应点的坐标为：（﹣2，2），位于第二象限．故选：B．【点评】本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．4．从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，这个点在圆x2+y2=2016内部的概率是（）A． B． C． D．【考点】列举法计算基本事件数及事件发生的概率．【专题】概率与统计．【分析】从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，基本事件总数n=5，再用列举法求出这个点在圆x2+y2=2016内部，包含的基本事件个数，由此利用等可能事件概率计算公式能求出这个点在圆x2+y2=2016内部的概率．【解答】解：从（40，30），（50，10），（20，30），（45，5），（10，10）这5个点中任取一个点，基本事件总数n=5，这个点在圆x2+y2=2016内部，包含的基本事件有：（20，30），（10，10），共2个，∴这个点在圆x2+y2=2016内部的概率p=．故选：B．【点评】本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．5．已知双曲线的渐近线方程为y=±x，且经过点（4，1），则双曲线的标准方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1【考点】双曲线的简单性质．【专题】计算题；圆锥曲线的定义、性质与方程．【分析】设双曲线方程为y2﹣x2=λ，代入点（4，1），求出λ，即可求出双曲线的标准方程．【解答】解：设双曲线方程为y2﹣x2=λ，代入点（4，1），可得1﹣=λ，∴λ=﹣3，∴双曲线的标准方程是=1．故选：C．【点评】本题考查双曲线的标准方程，考查学生的计算能力，正确设出双曲线的方程是关键．6．各顶点都在一个球面上的正四棱柱的高是2，体积是16，则这个球的表面积是（）A．16πB．20πC．24πD．32π【考点】球的体积和表面积．【专题】空间位置关系与距离．【分析】先求出正四棱柱的底面边长，再求其对角线的长，就是外接球的直径，然后求出球的表面积．【解答】解：各顶点都在一个球面上的正四棱柱高为2，体积为16，它的底面边长是：2，所以它的体对角线的长是：2，球的直径是：2，所以这个球的表面积是：4π（）2=20π故选：B．【点评】本题考查正四棱柱的外接球的表面积．考查计算能力，是基础题7．设等差数列{a n}的公差是d，其前项和是S n，若a1=d=1，则的最小值是（）A． B． C．2+ D．2﹣【考点】等差数列的性质．【专题】等差数列与等比数列．【分析】利用等差数列的通项公式及其前n项和公式可得：a n=n，S n=，于是=，再利用基本不等式的性质即可得出．【解答】解：a n=1+（n﹣1）=n，S n=，∴===，当且仅当n=4时取等号．∴的最小值是．故选：A．【点评】本题考查了等差数列的通项公式及其前n项和公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．8．已知a，b∈R+，函数f（x）=alog2x+b的图象经过点（4，1），则+的最小值为（）A．6﹣2B．6 C．4+2D．8【考点】基本不等式在最值问题中的应用．【专题】不等式的解法及应用．【分析】利用函数的图象经过的点，得到a、b关系式，然后求出最值．【解答】解：a，b∈R+，函数f（x）=alog2x+b的图象经过点（4，1），可得2a+b=1，则+=（+）（2a+b）=2+2+≥=8，当且仅当b=2a=时取等号，表达式的最小值为8．故选：D．【点评】本题考查基本不等式在最值中的应用，考查计算能力．9．对一名学生数学成绩统计了8次，第i次统计得到的数据为a i，具体如下表所示：在对上述统计数据的分析中，一部分计算见如图所示的算法流程图（其中是这8个数据的平均数），则输出的S的值是（）A．9 B．8 C．7 D．6【考点】程序框图．【专题】计算题；算法和程序框图．【分析】由题意及程序框图知，该程序框图的功能是输出这8个数据的方差，由公式结合题设中的数据计算出方差，选出正确选项．【解答】解：该程序框图的功能是输出这8个数据的方差，因为这8个数据的平均数==104，故其方差[（100﹣104）2+（101﹣104）2+（103﹣104）2+（103﹣104）2+（104﹣104）2+（106﹣104）2+（107﹣104）2+（108﹣104）2]=7，输出的S的值为7．故选C【点评】本题考查循环结构，理解题意，由框图得出本题所研究问题的算法是解题的关键．10．对任意的实数x都有f（x+2）﹣f（x）=2f（1），若y=f（x﹣1）的图象关于x=1对称，且f（0）=2，则f（2015）+f（2016）=（）A．0 B．2 C．3 D．4【考点】抽象函数及其应用．【专题】函数的性质及应用．【分析】根据条件判断函数f（x）是偶函数，结合条件关系求出函数的周期，进行转化计算即可．【解答】解：y=f（x﹣1）的图象关于x=1对称，则函数y=f（x）的图象关于x=0对称，即函数f（x）是偶函数，令x=﹣1，则f（﹣1+2）﹣f（﹣1）=2f（1），即f（1）﹣f（1）=2f（1）=0，即f（1）=0，则f（x+2）﹣f（x）=2f（1）=0，即f（x+2）=f（x），则函数的周期是2，又f（0）=2，则f（2015）+f（2016）=f（1）+f（0）=0+2=2，故选：B．【点评】本题主要考查函数值的计算，根据抽象函数关系判断函数的周期性和奇偶性是解决本题的关键．11．一个几何体的正视图和俯视图如图所示，其中俯视图是边长为2的正三角形及其内切圆，则侧视图的面积为（）A．6+πB． C．6+4π D．【考点】由三视图求面积、体积．【专题】计算题；空间位置关系与距离．【分析】几何体是三棱柱与球的组合体，判断三棱柱的高及底面三角形的边长，计算球的半径，根据侧视图是矩形上边加一个圆，分别计算矩形与圆的面积再相加．【解答】解：由三视图知：几何体是三棱柱与球的组合体，其中三棱柱的高为2，底面三角形的边长为2，根据俯视图是一个圆内切于一个正三角形，球的半径R==1，几何体的侧视图是矩形上边加一个圆，矩形的长、宽分别为2，3，圆的半径为1，侧视图的面积S=2×3+π×12=6+π．故选：A．【点评】本题考查了由正视图与俯视图求侧视图的面积，判断数据所对应的几何量及求得相关几何量的数据是解题的关键．12．函数f（x）=，若方程f（x）=﹣x+a有且只有两个不等的实数根，则实数a的取值范围为（）A．（﹣∞，0）B．[0，1）C．（﹣∞，1）D．[0，+∞）【考点】根的存在性及根的个数判断．【专题】数形结合；函数的性质及应用．【分析】由题知f（x）为分段函数，当x＜0时，由f（x）=f（x+1）可知f（x）为周期函数；当x大于等于0时函数为增函数，而方程f（x）=﹣x+a有且只有两个不相等的实数根即f（x）与y=﹣x+a由两个交点，在同一坐标系中画出函数f（x）的图象与函数y=﹣x+a 的图象，利用数形结合，易求出满足条件实数a的取值范围．【解答】解：函数f（x）=的图象如图所示，作出直线l：y=a﹣x，向左平移直线l观察可得函数y=f（x）的图象与函数y=﹣x+a的图象有两个交点，即方程f（x）=﹣x+a有且只有两个不相等的实数根，即有a＜1，故选：C．【点评】本题考查学生综合运用函数和方程的能力，以及让学生掌握数形结合的数学思想．二、填空题（本大题共4小题，每小题5分，共20分）13．函数f（x）=xe x的图象在x=1处的切线方程为2ex﹣y﹣e=0．【考点】利用导数研究曲线上某点切线方程．【专题】导数的综合应用．【分析】先求出切点的坐标，然后求出x=1处的导数，从而求出切线的斜率，利用点斜式方程即可求出切线方程．【解答】解：∵f（x）=xe x，∴f′（x）=e x+xe x，∴f′（1）=2e，又f（1）=e，∴曲线y=f（x）在点（1，f（1））处的切线方程为y﹣e=2e（x﹣1），即2ex﹣y﹣e=0．【点评】本题主要考查了利用导数研究曲线上某点切线方程，考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，正确求导和运用点斜式方程是解题的关键，属于中档题．14．若x，y满足约束条件，则z=2x+y的最大值为12．【考点】简单线性规划．【专题】不等式的解法及应用．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，求最大值．【解答】解：作出不等式组对应的平面区域如图：（阴影部分）．由z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最大，此时z最大．由，解得，即A（3，6），代入目标函数z=2x+y得z=2×3+6=6+6=12．即目标函数z=2x+y的最大值为12．故答案为：12．【点评】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．15．已知抛物线y2=﹣2px（p＞0）的准线与圆（x﹣5）2+y2=25相切，则p的值为20．【考点】抛物线的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】由题意可得圆心（5，0）到直线x= 的距离等于半径5，即|5﹣|=5，由此求得p的值．【解答】解：∵抛物线y2=﹣2px（p＞0）的准线x= 与圆（x﹣5）2+y2=25相切，∴圆心（5，0）到直线x= 的距离等于半径5，即|5﹣|=5，求得p=20 或p=0（舍去），故答案为：20．【点评】本题主要考查抛物线的标准方程和简单性质，直线和圆的位置关系，属于基础题．16．函数f（x）=sinx﹣acosx的图象的一条对称轴是x=，则g（x）=asinx+cosx=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤）的初相是．【考点】三角函数中的恒等变换应用；y=Asin（ωx+φ）中参数的物理意义．【专题】函数思想；综合法；三角函数的图像与性质．【分析】化简得f（x）=sin（x﹣θ），由对称轴得f（）=±求出a，代入g（x）化简可得答案．【解答】解：f（x）=sinx﹣acosx=sin（x﹣θ），（θ为辅助角），∵x=是f（x）的一条对称轴，∴sin﹣acos=±，即﹣﹣=±，化简得a2﹣2a+1=0，解得a=1，∴g（x）=sinx+cosx=sin（x+），∴g（x）的初相为．故答案为：．【点评】本题考查函数的对称性，考查辅助角公式和两角和差的正弦及余弦公式的运用，考查运算能力，属于基础题和易错题．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．在△ABC中，角A、B、C的对边分别为a、b、c．已知a+b=5，c=，且．（1）求角C的大小；（2）求△ABC的面积．【考点】解三角形；二倍角的余弦；余弦定理．【专题】计算题．【分析】（1）由三角形的内角和定理及诱导公式化简已知的等式，再根据二倍角的余弦函数公式化简，合并整理后得到关于cosC的方程，求出方程的解得到cosC的值，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数；（2）利用余弦定理表示出c2=a2+b2﹣2abcosC，再根据完全平方公式变形后，将a+b，c及cosC的值代入求出ab的值，然后再由ab，sinC的值，利用三角形的面积公式即可求出三角形ABC的面积．【解答】解：（1）∵A+B+C=180°，∴=90°﹣，由得：，∴，整理得：4cos2C﹣4cosC+1=0，解得：，∵0°＜C＜180°，∴C=60°；（2）由余弦定理得：c2=a2+b2﹣2abcosC，即7=a2+b2﹣ab，∴7=（a+b）2﹣3ab=25﹣3ab⇔ab=6，∴．【点评】此题属于解三角形的题型，涉及的知识有：诱导公式，二倍角的余弦函数公式，余弦定理，三角形的面积公式，以及完全平方公式的运用，熟练掌握公式及定理是解本题的关键．18．已知在四棱锥S﹣ABCD中，四边形ABCD是菱形，SD⊥平面ABCD，P为SB的中点，Q为BD上一动点．AD=2，SD=2，∠DAB=．（Ⅰ）求证：AC⊥PQ；（Ⅱ）当PQ∥平面SAC时，求四棱锥P﹣AQCD的体积．【考点】棱柱、棱锥、棱台的体积；空间中直线与直线之间的位置关系．【专题】综合题；转化思想；综合法；立体几何．【分析】（Ⅰ）证明AC⊥平面SBD，即可证明：AC⊥PQ；（Ⅱ）当PQ∥平面SAC时，设AC∩BD=O，取BO的中点Q，即可求四棱锥P﹣AQCD的体积．【解答】（Ⅰ）证明：∵四边形ABCD 是菱形， ∴AC ⊥BD ， ∵SD ⊥平面ABCD ， ∴SD ⊥AC ， ∵BD ∩SD=D ， ∴AC ⊥平面SBD ， ∵PQ ⊂平面SBD ， ∴AC ⊥PQ ；（Ⅱ）解：设AC ∩BD=O ，取BO 的中点Q ， ∴PQ ∥SO ，∵SO ⊂平面SAC ，PQ ⊄平面SAC ， ∴PQ ∥平面SAC ，连接PO ，则PO ∥SD ，且PO=SD=1，PO ⊥平面ABCD ， ∵S 四边形AQCD =S 菱形ABCD =，∴V 四棱锥P ﹣AQCD =S 四边形AQCD ═．【点评】本题考查线面垂直的判定与性质，考查四棱锥P ﹣AQCD 的体积，考查学生分析解决问题的能力，属于中档题．19．（Ⅰ）如表所示是某市最近5年个人年平均收入表节选．求y 关于x 的回归直线方程，并估计第6年此市的个人年平均收入（保留三位有效数字）．其中x i y i =421，x i 2=55附1： =， =﹣（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表：完成上表，并回答：是否有95%以上的把握认为“收入与接受培训时间有关系”．附2：附3： K 2=．（n=a+b+c+d ）【考点】独立性检验的应用． 【专题】概率与统计．【分析】（1）根据已知数据求出回归直线方程，将x=6代入，可估计第6年此市的个人年平均收入；（2）通过所给的数据计算K 2观测值，同临界值表中的数据进行比较，可得到结论． 【解答】解：（1）由已知中数据可得： =3， =26.4， ∵x i y i =421，x i 2=55，∴====2.5，=﹣=26.4﹣7.5=18.9，∴=2.5x+18.9， 当x=6时， =33.9．即第6年此市的个人年平均收入约为33.9千元；（2）某行业个人平均收入与接受专业培训时间关系得到2×2列联表：根据列联表中的数据，得到K 2的观测值为 K 2=≈4.762＞3.841．故我们有95%的把握认为“收入与接受培训时间有关系”．【点评】本题考查的知识是回归分析和独立性检验，计算量较大，属于中档题．20．已知椭圆C满足：过椭圆C的右焦点F （，0）且经过短轴端点的直线的倾斜角为．（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为坐标原点，若点A 在直线y=2上，点B 在椭圆C 上，且OA ⊥OB ，求线段AB 长度的最小值． 【考点】椭圆的简单性质．【专题】方程思想；待定系数法；圆锥曲线的定义、性质与方程． 【分析】（Ⅰ）设椭圆方程为+=1（a ＞b ＞0），运用直线的斜率公式，求出a ，b ，即可求椭圆C 的方程；（Ⅱ）先表示出线段AB 长度，再利用基本不等式，求出最小值． 【解答】解：（Ⅰ）设椭圆方程为+=1（a ＞b ＞0），由题意可得c=，设短轴的端点为（0，﹣b ）， 可得=tan=1，解得b=，∴a==2，∴椭圆方程为+=1；（Ⅱ）设A（t，2），B（x0，y0），x0≠0，则∵OA⊥OB，∴•=0，∴tx0+2y0=0，∴t=﹣，∵x02+2y02=4，∴|AB|2=（x0﹣t）2+（y0﹣2）2=（x0+）2+（y0﹣2）2=x02+y02++4=x02+++4=++4（0＜x02≤4），因为+≥4（0＜x02≤4），当且仅当=，即x02=4时等号成立，所以|AB|2≥8．∴线段AB长度的最小值为2．【点评】本题考查椭圆的方程与性质，考查基本不等式的运用，考查学生的计算能力，属于中档题．21．己知函数f（x）=（a+1）lnx+x﹣，其中a∈R．（I）求f（x）的单调区间；（Ⅱ）若在[1，e]上存在x0，使得f（x0）＜0成立，求a的取值范围．【考点】利用导数研究函数的单调性；函数恒成立问题．【专题】导数的综合应用．【分析】（Ⅰ）先求出函数的单调区间，通过讨论a的范围，确定函数的单调性；（Ⅱ）通过讨论a的范围，得到f（x）在[1，e]的单调性，求出[1，e]的最小值即可求出a的范围．【解答】解：（Ⅰ）函数f（x）的定义域是（0，+∞），f′（x）=+1+=，①a≥0时，f′（x）＞0在（0，+∞）恒成立，∴f（x）在（0，+∞）递增；②a＜0时，令f′（x）＞0，解得：x＞﹣a，令f′（x）＜0，解得：x＜﹣a，∴f（x）在（0，﹣a）递减，在（﹣a，+∞）递增；（Ⅱ）①由（Ⅰ）得：﹣a≤1即a≥﹣1时：f（x）在[1，e]递增，若在[1，e]上存在x0，使得f（x0）＜0成立，只需f（1）=1﹣a＜0即可，解得：a＞1；②若1＜﹣a＜e即﹣e＜a＜﹣1时：f（x）在[1，﹣a）递减，在（﹣a，e]递增，若在[1，e]上存在x0，使得f（x0）＜0成立，只需f（﹣a）＜0即可，即（a+1）ln（﹣a）+（﹣a）+1＜0，即ln（﹣a）＞1﹣，而1＜﹣a＜e，则0＜ln（﹣a）＜1，1﹣＞1，∴ln（﹣a）＞1﹣，无解；③若﹣a≥e，即a≤﹣e时：f（x）在[1，e]递减，若在[1，e]上存在x0，使得f（x0）＜0成立，只需f（e）＜0即可，即（a+1）+e﹣＜0，解得：a＜﹣；综上：a＞1或a＜﹣．【点评】本题考查了函数的单调性、最值问题，考查导数的应用，分类讨论思想，是一道中档题．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一个计分.【选修4-1几何证明选讲】22．如图，过圆外一点P的直线交圆O于A、B两点，PE是圆O的切线，CP平分∠APE，分别与AE、BE交于点C，D．求证：（1）CE=DE；（2）=．【考点】相似三角形的判定．【专题】证明题；数形结合；综合法；推理和证明．【分析】（1）由弦切角定理得∠A=∠BEP，由角平分线性质得到∠ECD=∠EDC，由此能证明EC=ED．（2）由已知条件推导出△PBD∽△PEC，△PDE∽△PCA，由此能证明=．【解答】证明：（1）∵PE是圆O的切线，∴∠A=∠BEP，∵PC平分∠APE，∴∠A+∠CPA=∠BEP+∠DPE，∵∠ECD=∠A+∠CPA，∠EDC=∠BEP+∠DPE，∴∠ECD=∠EDC，∴EC=ED．（2）∵∠PDB=∠EDC，∠EDC=∠ECD，∠PDB=∠PCE，∴∠BPD=∠EPC，∴△PBD∽△PEC，∴，同理，△PDE∽△PCA，∴，∴=．【点评】本题考查两条线段相等的证明，考查线段比值相等的证明，是基础题，解题时要认真审题，注意弦切角定理和三角形相似的性质定理的合理运用．【选修4─4：坐标系与参数方程选讲】23．设平面直角坐标系原点与极坐标极点重合，x 轴正半轴与极轴重合，若已知曲线C 的极坐标方程为ρ2=，点F 1、F 2为其左、右焦点，直线l 的参数方程为（t 为参数，t ∈R ）．（Ⅰ）求曲线C 的标准方程和直线l 的普通方程；（Ⅱ）若点P 为曲线C 上的动点，求点P 到直线l 的最大距离． 【考点】参数方程化成普通方程；简单曲线的极坐标方程． 【专题】方程思想；转化思想；坐标系和参数方程．【分析】（I ）利用即可把曲线C 的极坐标方程化为直角坐标方程；消去参数即可得到直线l 的普通方程．（II ）设P，θ∈[0，2π），则点P 到直线l 的距离d==，再利用三角函数的单调性即可得出．【解答】解：（I ）曲线C 的极坐标方程为ρ2=，化为直角坐标方程：3x 2+4y 2=12，即=1．直线l 的参数方程为（t 为参数，t ∈R ），化为普通方程：x ﹣1﹣y=0．（II ）设P，θ∈[0，2π），则点P 到直线l 的距离d==≤=，其中α=arctan．∴点P 到直线l 的最大距离是．【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式、三角函数的单调性，考查了推理能力与计算能力，属于中档题．．【选修4-5：不等式选讲】24．设函数f（x）=|2x﹣1|，x∈R．（Ⅰ）求不等式|f（x）﹣2|≤5的解集；（Ⅱ）若g（x）=的定义域为R，求实数m的取值范围．【考点】绝对值不等式的解法；函数的定义域及其求法．【专题】三角函数的图像与性质．【分析】（Ⅰ）不等式|f（x）﹣2|≤5，即|2x﹣1|≤7，即﹣7≤2x﹣1≤7，由此求得不等式的解集．（Ⅱ）由题意可得f（x）+f（x﹣1）+m≠0 恒成立，即|x﹣|+|x﹣|≠﹣恒成立．根据绝对值的意义求得|x﹣|+|x﹣|的最小值为1，可得﹣＜1，由此求得m的范围．【解答】解：（Ⅰ）不等式|f（x）﹣2|≤5，即﹣5≤f（x）﹣2≤5，即﹣3≤f（x）≤7，即|2x﹣1|≤7，即﹣7≤2x﹣1≤7，求得﹣3≤x≤4，故不等式的解集为{x|﹣3≤x≤4}．（Ⅱ）若g（x）=的定义域为R，则f（x）+f（x﹣1）+m≠0 恒成立，即|2x﹣1|+|2（x﹣1）﹣1|≠﹣m，即|x﹣|+|x﹣|≠﹣恒成立．根据绝对值的意义，|x﹣|+|x﹣|表示数轴上的x对应点到、对应点的距离之和，它的最小值为1，故﹣＜1，求得m＞﹣2．【点评】本题主要考查绝对值的意义，绝对值不等式的解法，函数的恒成立问题，体现了转化的数学思想，属于中档题．。