高中数学学业水平备考逐题突破-立体几何大题

(名师选题)（精选试题附答案）高中数学第八章立体几何初步经典大题例题单选题1、已知三棱锥P−ABC，其中PA⊥平面ABC，∠BAC=120°，PA=AB=AC=2，则该三棱锥外接球的表面积为（）A．12πB．16πC．20πD．24π答案：C分析：根据余弦定理、正弦定理，结合球的性质、球的表面积公式进行求解即可.根据题意设底面△ABC的外心为G，O为球心，所以OG⊥平面ABC，因为PA⊥平面ABC，所以OG//PA，设D是PA中点，因为OP=OA，所以DO⊥PA，因为PA⊥平面ABC，AG⊂平面ABC，所以AG⊥PA，因此OD//AG，PA=1，因此四边形ODAG是平行四边形，故OG=AD=12由余弦定理，得BC=√AB2+AC2−2AB⋅AC⋅cos120°=√4+4−2×2×2×(−1)=2√3，2⇒AG=2，由正弦定理，得2AG=√3√32所以该外接球的半径R满足R2=(OG)2+(AG)2=5⇒S=4πR2=20π，故选：C．小提示：关键点睛：运用正弦定理、余弦定理是解题的关键.2、如图所示的正方形SG1G2G3中，E ， F分别是G1G2，G2G3的中点，现沿SE，SF，EF把这个正方形折成一个四面体，使G1，G2，G3重合为点G，则有（）A．SG⊥平面EFG B．EG⊥平面SEFC．GF⊥平面SEF D．SG⊥平面SEF答案：A解析：根据正方形的特点，可得SG⊥FG，SG⊥EG，然后根据线面垂直的判定定理，可得结果.由题意：SG⊥FG，SG⊥EG，FG∩EG=G，FG，EG⊂平面EFG所以SG⊥平面EFG正确，D不正确；.又若EG⊥平面SEF，则EG⊥EF，由平面图形可知显然不成立；同理GF⊥平面SEF不正确；故选：A小提示：本题主要考查线面垂直的判定定理，属基础题.3、若一个正方体的体对角线长为a，则这个正方体的全面积为（）A ．2a 2B ．2√2a 2C ．2√3a 2D ．3√2a 2答案：A分析：设正方体的棱长为x ，求出正方体的棱长即得解.解：设正方体的棱长为x ，则√3x =a ，即x 2=13a 2，所以正方体的全面积为6x 2=6×13a 2=2a 2． 故选：A4、《九章算术·商功》中，将四个面都为直角三角形的四面体称为鳖臑．如图，在鳖臑ABCD 中，AB ⊥平面BCD ，AC ⊥CD ，AC ＝BC ＋CD ＝2，当△BCD 的面积最大时，鳖臑ABCD 的表面积为（ ）A ．√3+√62B ．3+√62C ．2+√3+√62D ．3+√3+√62答案：D分析：根据题意可证明CD ⊥BC ，从而说明三角形BCD 是直角三角形，求得BD ，进而求得四个直角三角形的面积，可得答案.由题意可知：AB ⊥平面BCD ，CD ⊂平面BCD ，故AB ⊥CD ,又AC ⊥CD ，AC ∩AB =A,AB,AC ⊂平面ABC ，故CD ⊥平面ABC ，BC ⊂平面ABC ，故CD ⊥BC ,所以S △BCD =12BC ⋅CD ≤12×(BC+CD 2)2=12 ,当且仅当BC =CD =1时取得等号， 故BD =√1+1=√2 ,由AB ⊥平面BCD ，可知AB ⊥BD,AB ⊥BC ,故AB=√AC2−BC2=√4−1=√3 ,所以S△ABD=12AB⋅BD=√62,S△ABC=12AB⋅BC=√32,S△BCD=12BC⋅CD=12,S△ACD=12AC⋅CD=1,所以鳖臑ABCD的表面积为√62+√32+12+1=3+√3+√62，故选：D5、锐角△ABC中，角A、B、C所对的边分别为a、b、c，若a=7、b=8，m⃑⃑ =(12,cosA)，n⃑=(sinA，−√32)，且m⃑⃑ ⊥n⃑，则△ABC的面积为（）A．√3B．3√3C．5√3D．10√3答案：D分析：先由向量垂直得到A=π3，利用余弦定理求出c=3或c=5，利用锐角三角形排除c=3，从而c=5，利用面积公式求出答案.由题意得：12sinA−√32cosA=0，故tanA=√3，因为A∈(0,π2)，所以A=π3，由余弦定理得：cosA=64+c 2−492×8c =12，解得：c=3或c=5，当c=3时，最大值为B，其中cosB=49+9−642×7×3<0，故B为钝角，不合题意，舍去；当c=5时，最大值为B，其中cosB=49+25−642×7×5>0，故B为锐角，符合题意，此时S△ABC=12bcsinA=12×8×5×√32=10√3.故选：D6、过半径为4的球O表面上一点M作球O的截面，若OM与该截面所成的角是30°，则O到该截面的距离是（）A．4B．2√3C．2D．1答案：C分析：作出球的截面图，根据几何性质计算，可得答案.作出球的截面图如图：设A为截面圆的圆心，O为球心，则OA⊥截面，AM在截面内，即有OA⊥AM，=2 ,故∠OMA=30∘,所以OA=4×12即O到该截面的距离是2，故选：C7、如图，点N为正方形ABCD的中心，ΔECD为正三角形，平面ECD⊥平面ABCD,M是线段ED的中点，则A．BM=EN，且直线BM,EN是相交直线B．BM≠EN，且直线BM,EN是相交直线C．BM=EN，且直线BM,EN是异面直线D．BM≠EN，且直线BM,EN是异面直线答案：B解析：利用垂直关系，再结合勾股定理进而解决问题．如图所示， 作EO ⊥CD 于O ，连接ON ，过M 作MF ⊥OD 于F ．连BF ，∵平面CDE ⊥平面ABCD ．EO ⊥CD,EO ⊂平面CDE ，∴EO ⊥平面ABCD ，MF ⊥平面ABCD ，∴ΔMFB 与ΔEON 均为直角三角形．设正方形边长为2，易知EO =√3, ON =1 EN =2，MF =√32,BF =52,∴BM =√7．∴BM ≠EN ，故选B ．小提示：本题考查空间想象能力和计算能力， 解答本题的关键是构造直角三角形．8、在正方体ABCD −A 1B 1C 1D 1中，E 为线段A 1B 1的中点，则异面直线D 1E 与BC 1所成角的余弦值为（ ）A ．√55B ．√105C ．√155D ．2√55答案：B分析：连接AD 1，AE ，得到AD 1//BC 1，把异面直线D 1E 与BC 1所成角转化为直线D 1E 与AD 1所成角，取AD 1的中点F ，在直角△D 1EF 中，即可求解.在正方体ABCD −A 1B 1C 1D 1中，连接AD 1，AE ，可得AD 1//BC 1，所以异面直线D 1E 与BC 1所成角即为直线D 1E 与AD 1所成角，即∠AD 1E 为异面直线D 1E 与BC 1所成角，不妨设AA 1=2，则AD 1=2√2，D 1E =AE =√5，取AD 1的中点F ，因为D 1E =AE ，所以EF ⊥AD 1，在直角△D 1EF 中，可得cos∠AD 1E =D 1F D 1E =√2√5=√105. 故选：B.9、若直线a //平面α，A ∉α，且直线a 与点A 位于α的两侧，B ，C ∈a ，AB ，AC 分别交平面α于点E ，F ，若BC =4，CF =5，AF =3，则EF 的长为（ ）A ．3B ．32C ．34D ．23答案：B分析：根据线面平行可得线线平行，从而可求EF =32. ∵BC //α，BC ⊂平面ABC ，平面ABC ∩α=EF ，∴EF //BC ，∴AF AC =EF BC ，即35+3=EF 4，∴EF =32. 故选：B.10、如图在正三棱锥S −ABC 中，M,N 分别是棱SC,BC 的中点，Q 为棱AC 上的一点，且AQ =12QC ，MN ⊥MQ ，若AB =2√2，则此正三棱锥S −ABC 的外接球的体积为（ ）A ．12πB ．4√33πC ．8√3πD ．4√3π 答案：D分析：根据题意证明SA,SB,SC 两两垂直，将三棱锥放入棱长为2的正方体，两者外接球体积相同，求得正方体外接球体积即可得出答案.因为在△SBC 中，M,N 分别是棱SC,BC 的中点，所以MN //SB ，因为MN ⊥MQ ，所以SB ⊥MQ ，因为三棱锥S −ABC 为正三棱锥，所以SB ⊥AC （对棱垂直），又因为MQ,AC ⊂面SAC ，MQ ∩AC =Q ，所以SB ⊥面SAC ，因为SA,SC ⊂面SAC ，所以SB ⊥SA,SB ⊥SC ，在Rt △SAB 中，SA 2+SB 2=AB 2，因为三棱锥S −ABC 为正三棱锥，所以△SBC 是等腰三角形，△ABC 是等边三角形，所以SB =SC ，AB =AC ,所以SA 2+SC 2=AC 2，即SA ⊥SC ，所以SA,SB,SC 两两垂直，将此三棱锥放入正方体中，此正方体的面对角线长等于AB 长，为2√2,则该正方体棱长为2，外接球半径R =√(22)2+(2√22)2=√3，正方体外接球体积V =43πR 3=43π×(√3)3=4√3π,此正三棱锥S −ABC 的外接球体积和正方体外接球体积相同，为4√3π.故选：D填空题11、如图所示，过三棱台上底面的一边A1C1，作一个平行于棱BB1的截面，与下底面的交线为DE．若D、E分别是AB、BC的中点，则V A1B1C1−DBEV A1B1C1−ABC=______．答案：37分析：证得S△A1B1C1=14S△ABC，然后结合棱台与棱柱的体积公式即可求出结果.因为BB1//平面DEC1A1，且平面BB1C1C∩平面DEC1A1=C1E，所以BB1//C1E，又因为B1C1//BE，所以四边形BB1C1E为平行四边形，所以B1C1=BE，且E分别是BC的中点，所以B1C1=1 2BC，同理A1B1=12AB，因此S△A1B1C1=14S△ABC，设上底面的面积为S，高为ℎ，则下底面的面积为4S，所以V A1B1C1−DBEV A1B1C1−ABC =13(S+√S⋅4S+4S)ℎ=37，所以答案是：37.12、两个平面最多可以将空间分为___________部分.答案：4分析：根据两个平面的位置关系分别计算出它们将空间分成的部分数即可得解. 两个平面的位置关系有平行和相交两种，当两个平面平行时，它们可将空间分成3部分，当两个平面相交时，它们可将空间分成4部分，所以两个平面最多可以将空间分为4部分.所以答案是：413、在四棱锥P-ABCD中，PA⊥平面ABCD，底面四边形ABCD为矩形．请在下面给出的5个条件中选出2个作为一组，使得它们能成为“在BC边上存在点Q，使得△PQD为钝角三角形”的充分条件___________．（写出符合题意的一组即可）①PA=2；②BC=3；③BC=√5；④AB=√2；⑤AB=1.答案：②④或②⑤或③⑤分析：设PA=a,AB=b,AD=c，BQ=x(0≤x≤c)，则CQ=c−x，计算出PQ2，DQ2，PD2，若在BC边上存在点Q，使得△PQD为钝角三角形，则PQ2+DQ2<PD2，解不等式再根据已知条件可得答案.设PA=a,AB=b,AD=c，BQ=x(0≤x≤c)，则CQ=c−x，因为PA⊥平面ABCD，底面四边形ABCD为矩形，所以PA⊥AQ，则PQ2=PA2+AQ2=PA2+AB2+BQ2=a2+b2+x2，DQ2=CD2+CQ2=b2+(c−x)2，PD2=PA2+AD2=a2+c2，若在BC边上存在点Q，使得△PQD为钝角三角形，则PQ2+DQ2<PD2，即a2+b2+x2+b2+(c−x)2<a2+c2，整理得x2−cx+b2<0(0<x<c)，要使不等式有解，只需c2−4b2>0，即只需BC>2AB即可，因为①PA=2；②BC=3；③BC=√5；④AB=√2；⑤AB=1，所以②④或②⑤或③⑤.所以答案是：②④或②⑤或③⑤.14、所有棱长均为2的正三棱锥的体积为______.答案：23√2##2√23分析：棱长均为2的正三棱锥，分别求出棱锥的底面面积和高，代入棱锥体积公式，即可得到答案. 当三棱锥棱长均为2时，正三棱锥即为正四面体，如图，正四面体的底面积S=√34×22=√3，正四面体的高ℎ=PO=√PA2−AO2=√22−(23×√32×2)2=2√63，故正四面体的体积V=13⋅S⋅ℎ=2√23.所以答案是：2√2315、已知球O的半径为43,点A,B,C,D均在球面上，若△ABC为等边三角形，且其面积为√3,则三棱锥D−ABC的最大体积是___________.答案：2√33分析：根据三角形面积求出边长，即可求出三角形外接圆半径，继而可求出高的最大值，求出体积.设△ABC外接圆的圆心为O1,由△ABC是面积为√3的等边三角形，得12⋅|AB|2⋅sin60∘=√3,解得AB=2，则|O1B|=12×|AB|sin60∘=2√33.当三棱棱锥D−ABC体积最大时，球心O在DO1上，因此有|OO1|=√|OB|2−|O1B|2=23,所以|DO1|的最大值为43+23=2，三棱锥D−ABC的最大体积为V=13⋅S△ABC⋅|DO1|=13×√3×2=2√33.所以答案是：2√33.小提示：本题考查三棱锥的外接球问题，解题的关键是建立好勾股关系求出高.解答题16、如图，在正方体ABCD−A1B1C1D1中，E为BB1的中点．（Ⅰ）求证：BC1//平面AD1E；（Ⅱ）求直线AA1与平面AD1E所成角的正弦值．答案：（Ⅰ）证明见解析；（Ⅱ）23.分析：（Ⅰ）证明出四边形ABC1D1为平行四边形，可得出BC1//AD1，然后利用线面平行的判定定理可证得结论；也可利用空间向量计算证明；（Ⅱ）可以将平面扩展，将线面角转化，利用几何方法作出线面角，然后计算；也可以建立空间直角坐标系，利用空间向量计算求解 . （Ⅰ）[方法一]：几何法 如下图所示：在正方体ABCD −A 1B 1C 1D 1中，AB //A 1B 1且AB =A 1B 1，A 1B 1//C 1D 1且A 1B 1=C 1D 1， ∴AB //C 1D 1且AB =C 1D 1，所以，四边形ABC 1D 1为平行四边形，则BC 1//AD 1， ∵BC 1⊄平面AD 1E ，AD 1⊂平面AD 1E ，∴BC 1//平面AD 1E ； [方法二]:空间向量坐标法以点A 为坐标原点，AD 、AB 、AA 1所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系A −xyz ，设正方体ABCD −A 1B 1C 1D 1的棱长为2，则A (0,0,0)、A 1(0,0,2)、D 1(2,0,2)、E (0,2,1)，AD 1⃑⃑⃑⃑⃑⃑⃑ =(2,0,2)，AE ⃑⃑⃑⃑⃑ =(0,2,1)，设平面AD 1E 的法向量为n ⃑ =(x,y,z )，由{n →⋅AD 1→=0n →⋅AE →=0，得{2x +2z =02y +z =0， 令z =−2，则x =2，y =1，则n →=(2,1,−2).又∵向量BC 1⃑⃑⃑⃑⃑⃑⃑ =(2,0,2),BC 1⃑⃑⃑⃑⃑⃑⃑ ·n ⃑ =2×2+0×1+2×(−2)=0, 又∵BC 1⊄平面AD 1E ，∴BC 1//平面AD 1E ； （Ⅱ）[方法一]：几何法延长CC 1到F ，使得C 1F =BE ，连接EF ，交B 1C 1于G ， 又∵C 1F//BE ，∴四边形BEFC 1为平行四边形，∴BC 1//EF ， 又∵BC 1//AD 1,∴AD 1//EF ,所以平面AD 1E 即平面AD 1FE , 连接D 1G ，作C 1H ⊥D 1G ,垂足为H ,连接FH ,∵FC 1⊥平面A 1B 1C 1D 1,D 1G ⊂平面A 1B 1C 1D 1,∴FC 1⊥D 1G ， 又∵FC 1∩C 1H =C 1,∴直线D 1G ⊥平面C 1FH , 又∵直线D 1G ⊂平面D 1GF ,∴平面D 1GF ⊥平面C 1FH ,∴C 1在平面D 1GF 中的射影在直线FH 上,∴直线FH 为直线FC 1在平面D 1GF 中的射影，∠C 1FH 为直线FC 1与平面D 1GF 所成的角，根据直线FC 1//直线AA 1，可知∠C 1FH 为直线AA 1与平面AD 1G 所成的角. 设正方体的棱长为2，则C 1G =C 1F =1,D 1G =√5,∴C 1H =√5=√5,∴FH =√1+(√5)2=√5,∴sin∠C 1FH =C 1H FH=23,即直线AA 1与平面AD 1E 所成角的正弦值为23.[方法二]：向量法接续（I)的向量方法，求得平面平面AD 1E 的法向量n ⃑ =(2,1,−2)，又∵AA 1⃑⃑⃑⃑⃑⃑⃑ =(0,0,2),∴cos <n ⃑ ,AA 1⃑⃑⃑⃑⃑⃑⃑ >=n ⃑ ⋅AA 1⃑⃑⃑⃑⃑⃑⃑⃑ |n ⃑ |⋅|AA 1⃑⃑⃑⃑⃑⃑⃑⃑ |=−43×2=−23， ∴直线AA 1与平面AD 1E 所成角的正弦值为23.[方法三]：几何法+体积法如图，设B 1C 1的中点为F ，延长A 1B 1,AE,D 1F ，易证三线交于一点P ． 因为BB 1∥AA 1,EF ∥AD 1，所以直线AA 1与平面AD 1E 所成的角，即直线B 1E 与平面PEF 所成的角． 设正方体的棱长为2，在△PEF 中，易得PE =PF =√5,EF =√2， 可得S △PEF =32．由V 三棱锥B 1−PEF =V 三棱锥P−B 1EF ，得13×32⋅B 1H =13×12×1×1×2， 整理得B 1H =23． 所以sin∠B 1EH =B 1H B 1E =23．所以直线AA 1与平面AD 1E 所成角的正弦值为23．[方法四]：纯体积法设正方体的棱长为2，点A 1到平面AED 1的距离为h ， 在△AED 1中，AE =√5,AD 1=2√2,D 1E =3， cos∠AED 1=D 1E 2+AE 2−AD 122D 1E⋅AE=2×3×√5=√55， 所以sin∠AED 1=2√55，易得S △AED 1=3．由V E−AA 1D 1=V A 1−AED 1，得13S △AD 1A 1⋅A 1B 1=13S △AED 1⋅ℎ，解得ℎ=43， 设直线AA 1与平面AED 1所成的角为θ，所以sinθ=ℎAA 1=23．【整体点评】（Ⅰ）的方法一使用线面平行的判定定理证明，方法二使用空间向量坐标运算进行证明； （II ）第一种方法中使用纯几何方法，适合于没有学习空间向量之前的方法，有利用培养学生的集合论证和空间想象能力，第二种方法使用空间向量方法，两小题前后连贯，利用计算论证和求解，定为最优解法；方法三在几何法的基础上综合使用体积方法，计算较为简洁；方法四不作任何辅助线，仅利用正余弦定理和体积公式进行计算，省却了辅助线和几何的论证，不失为一种优美的方法. 17、已知正方体ABCD −A ′B ′C ′D ′.(1)G 是△BA ′C ′的重心，求证：直线DG ⊥平面BA ′C ′；(2)若AB =1，动点E ､F 在线段AD ､D ′C ′上，且DE =D ′F =a ，M 为AB 的中点，异面直线EF 与DM 所成的角为arccos√210，求a 的值.答案：(1)证明见解析(2)√24分析：（1）根据空间向量，以B ′A ′⃑⃑⃑⃑⃑⃑⃑⃑ =i ,B ′B ⃑⃑⃑⃑⃑⃑⃑ =j ,B ′C ′⃑⃑⃑⃑⃑⃑⃑⃑ =k ⃑ 为基底，用基底向量表示其他向量，根据向量的数量积为0判断线线垂直，进而证明线面垂直.（2）以空间直角坐标系，写成点的坐标，根据向量的夹角与异面直线夹角间的关系，列出方程即可求解.（1）证明：设B ′A ′⃑⃑⃑⃑⃑⃑⃑⃑ =i ,B ′B ⃑⃑⃑⃑⃑⃑⃑ =j ,B′C ′⃑⃑⃑⃑⃑⃑⃑⃑ =k ⃑ ， 显然i ⋅j =0，j ⋅k ⃑ =0，k ⃑ ⋅i =0，因为G 是△BA ′C ′的重心，所以B ′G ⃑⃑⃑⃑⃑⃑⃑ =13(i +j +k ⃑ ),故DG ⃑⃑⃑⃑⃑ =B ′G ⃑⃑⃑⃑⃑⃑⃑ −B ′D ⃑⃑⃑⃑⃑⃑⃑ =B ′G ⃑⃑⃑⃑⃑⃑⃑ −(B ′B ⃑⃑⃑⃑⃑⃑⃑ +BA ⃑⃑⃑⃑⃑ +AD ⃑⃑⃑⃑⃑ )=13(i +j +k ⃑ )−(j +i +k )=−23(i +j +k ⃑ ) A ′C ′⃑⃑⃑⃑⃑⃑⃑⃑ =k ⃑ −i ；DG ⃑⃑⃑⃑⃑ ⋅A ′C ′⃑⃑⃑⃑⃑⃑⃑⃑ =−23(k ⃑ 2−i 2)=0，得DG ⃑⃑⃑⃑⃑ ⊥A ′C ′⃑⃑⃑⃑⃑⃑⃑⃑ ， 同理DG ⃑⃑⃑⃑⃑ ⋅A ′B ⃑⃑⃑⃑⃑⃑⃑ =0，得DG ⃑⃑⃑⃑⃑ ⊥A ′B⃑⃑⃑⃑⃑⃑⃑ . 因为A ′C ′⃑⃑⃑⃑⃑⃑⃑⃑ 不平行于A ′B⃑⃑⃑⃑⃑⃑⃑ ，所以直线DG ⊥平面BA ′C ′. （2）以D 为坐标原点，射线DA 、DC 、DD ′分别是x 轴､y 轴､z 轴的正半轴，建立空间直角坐标系，于是E(a,0,0),F(0,a,1),M (1,12,0)，则EF⃑⃑⃑⃑⃑ =(−a,a,1),DM ⃑⃑⃑⃑⃑⃑ =(1,12,0).于是cos⟨EF⃑⃑⃑⃑⃑ ,DM ⃑⃑⃑⃑⃑⃑ ⟩=|EF⃑⃑⃑⃑⃑ ⋅DM ⃑⃑⃑⃑⃑⃑⃑ ||EF⃑⃑⃑⃑⃑ |⋅|DM ⃑⃑⃑⃑⃑⃑⃑ |=12a √52⋅√2a 2+1=√210，解得a =√24，所以a 的值为√24.18、如图所示，在四棱锥P −ABCD 中，底面ABCD 为正方形，E 为侧棱PC 的中点.（1）求证：经过A 、B 、E 三点的截面平分侧棱PD ；（2）若PA ⊥底面ABCD ，且PA =AD =2，求四面体ABEP 的体积. 答案：（1）证明见解析；（2）23.分析：（1）设截面ABE 与侧棱PD 交于点F ，连结EF,AF ，证明CD//EF.即得F 为PD 的中点，即截面ABE 平分侧棱PD ；（2）取PB 中点H ，连EH ，证明EH ⊥平面PAB ，即得解. （1）证明：设截面ABE与侧棱PD交于点F，连结EF,AF.因为底面ABCD为矩形，所以AB//CD.又AB⊄平面PCD，且CD⊂平面PCD，所以AB//平面PCD.又AB⊂平面ABE，且平面ABE∩平面PCD=EF，所以AB//EF.又因为AB//CD，所以CD//EF.因为E为PC的中点，所以F为PD的中点，即截面ABE平分侧棱PD. （2）∵PA⊥平面ABCD，BC⊆平面ABCD，∴BC⊥PA，又BC⊥AB，∴BC⊥平面PAB.取PB 中点H ，连EH ， ∵E 是PC 中点，∴EH//BC ，即EH =1且EH ⊥平面PAB ， 又Rt △PAB 的面积S =12PA ⋅AB =2.∴四面体ABEP 的体积V =V E−PAB =13⋅S ⋅EH =23.小提示：方法点睛：求几何体的体积常用的方法有：（1）规则的公式法；（2）不规则的割补法；（3）等体积法. 要根据已知条件灵活选择方法求解.19、如图，在正三棱柱ABC −A 1B 1C 1中，D 为棱AA 1的中点．若截面△BC 1D 是面积为6的直角三角形，求此三棱柱的表面积．答案：24√2+4√3分析：设AD =b,AB =a ，根据△BC 1D 是面积为6的直角三角形，由{BD 2+C 1D 2=BC 1212⋅BD ⋅C 1D =6求解.解：设AD =b,AB =a ，则BD =C 1D =√a 2+b 2，BC 1=√a 2+4b 2．由题意得{BD 2+C 1D 2=BC 12,12⋅BD ⋅C 1D =6, 即{a 2+b 2+a 2+b 2=a 2+4b 2,a 2+b 2=12,解得{a =2√2,b =2, 从而S 表=4×3×2√2+2×2√2×2√2×√34=24√2+4√3．。

专题07立体几何初步考点一：简单几何体的表面积和体积1．（2023·北京）已知三棱柱111ABC A B C -的体积为12，则三棱锥111A A B C -的体积为（）A ．3B ．4C ．6D ．8【答案】B【详解】三棱锥111A A B C -与三棱柱111ABC A B C -等底等高，则三棱锥111A A B C -的体积是三棱柱111ABC A B C -体积的13，即三棱锥111A A B C -的体积为4.故选：B2．（2023·河北）将一块棱长为60cm 的正方体石块，磨制成一个球形石块，则最大球形石块的体积是（取π3=）（）A ．3864000cmB ．3108000cm C ．310800cm D ．35400cm 【答案】B【详解】由题意可得，该问题相当于求正方体内切球体积，易知当石块直径等于正方体棱长时其体积最大，即最大球形石块的半径为30cm ，根据球的体积公式可得33334π430cm 108000cm 3V r ==⨯=.故选：B3．（2023春·福建）已知球体O 的半径为2，则球体O 的表面积为（）A ．4πB ．8πC ．16πD ．32π【答案】C【详解】设球体O 的半径为R ，所以2R =由球体O 的表面积公式可得24π16πS R ==.故选：C.4．（2022·北京）如图，在直三棱柱111ABC A B C -中，ABC 是等腰直角三角形．若14,3AB AC AA ===，则该直三棱柱的体积为（）A ．6B ．12C ．18D ．24【详解】因为在直三棱柱111ABC A B C -中，ABC 是等腰直角三角形，14,3AB AC AA ===，则BAC ∠为直角，故可得：11111114432422AB BC B A C A C V S AA AB AC AA -=⋅=⨯⨯⨯=⨯⨯⨯= ,故选：D5．（2022春·天津）已知圆锥的底面半径是1，高是2，则这个圆锥的体积为（）A ．2π3B ．πC ．4π3D ．2π【答案】A【详解】由题意知，圆锥底面积为2π1πS =⨯=，圆锥的高2h =，则圆锥的体积为311π2332πV Sh ==⨯⨯=.故选：A6．（2021·北京）如图，在三棱锥P ABC -中，23PC ABC AC BC AC BC PC ⊥⊥===平面，，，，则三棱锥P ABC -的体积为（）A ．1B ．2C ．6D ．12【答案】B【详解】解：因为PC ABC ⊥平面，所以PC 即为三棱锥 P ABC -高，所以11223232P ABC V -=⨯⨯⨯⨯=.故选：B.7．（2021春·天津）如图，圆柱O O '的底面半径是2，高是3，则这个圆柱的体积是（）A ．πB ．3πC ．4πD ．12π【答案】D【详解】由圆柱的体积公式可得，该圆柱的体积为：2π2312π⨯⨯=.8．（2023·山西）在三棱锥A BCD -中，AB ⊥平面BCD ，4AB CD ==，则三棱锥A BCD -的外接球的表面积的最小值为（）A ．16πB ．32πC ．112π3D ．64π【答案】B【详解】设底面BCD 的外接圆的半径为r ，,(0,π)CBD θθ∠=∈，则在BCD △中，4CD =，可得42sin r θ=，所以2sin r θ=，设底面三角形的外心为1O ，过1O 作底面BCD 的垂线，由于AB ⊥平面BCD ，故所作垂线与AB 的中垂线的交点即为三棱锥A BCD -外接球的球心，设外接球的半径为R ，而1122O O AB ==，则外接球的半径为221124422sin R O O O B θ=+=+≥，即当sin 1θ=即BC BD ⊥时，三棱锥的外接球的半径取得最小值22，此时三棱锥A BCD -的外接球表面积取得最小值：24π(22)32π⨯=,故选：B9．（2022春·浙江）某广场设置了一些石凳供大家休息，每个石凳都是由正方体截去八个一样的四面体得到的（如图，从棱的中点截）.如果被截正方体的棱长是4（单位：dm ），那么一个石凳的体积是（单位：3dm ）.【答案】1603【详解】正方体的体积为3464=，正方体截去的八个四面体是全等的正三棱锥，截去的一个正三棱锥的体积为114222323⨯⨯⨯⨯=，则石凳的体积为416064833-⨯=.故答案为：1603.10．（2022春·贵州）已知长方体的三条棱长分别为1，2，6，则该长方体外接球的表面积为．（结果用含π的式子表示）【答案】9π【详解】由题意得，长方体的体对角线即为外接球直径，设外接球半径为R ，则126322R ++==，则外接球的表面积为249R ππ=.故答案为：9π.11．（2021春·福建）半径为1的球的体积为．【答案】43π【详解】根据球的体积公式344V 33R ππ==．【点睛】球的体积公式34V 3Rπ=12．（2021秋·青海）如图，在圆柱内有一个球，该球与圆柱的上下底面及母线均相切，已知圆柱的底面半径为3，则圆柱的体积为．【答案】54π【详解】设圆柱的底面半径为r ，球的半径为R ．由条件有：3R r ==，圆柱的高为2R ，所以圆柱的体积为23π22π54πr R r ⨯==．故答案为：54π考点二：空间点、直线、平面的位置关系1．（2023·北京）四棱锥P ABCD -如图所示，则直线PC （）A ．与直线AD 平行B ．与直线AD 相交C ．与直线BD 平行D ．与直线BD 是异面直线【答案】D【详解】根据异面直线的定义，不同在任何一个平面内的两条直线叫做异面直线，可以判断直线PC 与直线AD 、直线BD 是异面直线.故选：D.2．（2023·河北）已知m ，n 是两条不同的直线，α是平面，则下列四个结论中正确的是（）A ．若m α⊥，n α⊥，则//m nB ．若//m α，//n α，则//m nC ．若m α⊥，m n ⊥，则//n αD ．若m ，n 与α所成的角相等，则//m n【答案】A【详解】由线面垂直的性质定理可得垂直于同一平面的两直线平行，即A 正确；若//m α，//n α，可知m ，n 的位置关系可以是平行、相交或异面，即B 错误；若m α⊥，m n ⊥，则直线n 可以在平面α内，所以C 错误；由线面角的定义可知，若m ，n 与α所成的角相等，则m ，n 的位置关系可以是平行、相交或异面，即D 错误.故选：A3．（2023·山西）已知三条不重合的直线m ，n ，l ，三个不重合的平面α，β，γ，则（）A ．若//m n ，n ⊂α，则//m αB ．若l α⊥，m β⊂，l m ⊥，则//αβC ．若αγ⊥，βγ⊥，l αβ⋂＝，则l γ⊥D ．若m α⊂，n ⊂α，//m β，//n β，则//αβ【答案】C【详解】对于A 中，若//m n ，n ⊂α，则//m α或m α⊂，所以A 项不正确；对于B 中，若l α⊥，m β⊂，l m ⊥，则//αβ或α与β相交，所以B 项不正确；对于C 中，设,a b αγβγ== ，在平面γ内任取一点P ，作,PA a PB a ⊥⊥，垂足分别为,A B ，由面面垂直的性质定理，可得,PA l PB l ⊥⊥，又因为PA PB P = ，可得l γ⊥，所以C 项正确；对于D 中，若m α⊂，n ⊂α，//m β，//n β，只有,m n 相交时，才有//αβ，所以D 项不正确.故选：C.4．（2023·江苏）已知直线l 平面α，直线m ⊂平面α，则l 与m 不可能（）A ．平行B ．相交C ．异面D ．垂直【答案】B【详解】直线l 平面α，直线m ⊂平面α，则l 与m 可能平行，异面和垂直，若l 与m 相交，l m A = ，则∈A l ，A m ∈，直线m ⊂平面α，故A α∈，即l 与α有交点，这与题设矛盾.故选：B5．（2023春·浙江）下列说法正确的是（）A ．一个平面里有三个不同的点到另一个平面的距离都相等，则这两个面平行B ．和同一条直线都相交的两条直线一定相交C ．经过空间中三个点有且只有一个平面D ．经过两条相交直线有且只有一个平面【答案】D【详解】对于A,一个平面里有三个不同的点到另一个平面的距离都相等，则这两个面可能相交也可能平行，例如在正方体中,平面11CDD C 中的点1,,C C M 到平面11ADD A 的距离均相等，但是平面11CDD C 与平面11ADD A 相交，不平行，故A 错误，对于B,和同一条直线都相交的两条直线不一定相交，例如正方体中,CD AB 均与BC 相交，但是,CD AB 不相交，故B 错误，对于C ，经过空间中三个不共线的点有且只有一个平面，故C 错误，对于D,两条相交直线可以确定一个平面,因此经过两条相交直线有且只有一个平面，故D 正确，故选：D6．（2023春·福建）已知四棱锥S ABCD -底面为正方形，SD ⊥平面ABCD ，则（）A ．SB SC ⊥B ．SD AB ⊥C ．SA ⊥平面ABCD D ．//SA 平面SBC【答案】B【详解】对于A 选项，因为SD ⊥平面ABCD ，BC ⊂平面ABCD ，则BC SD ⊥，因为四边形ABCD 为正方形，则BC CD ⊥，因为SD CD D = ，SD 、CD ⊂平面SCD ，所以，BC ⊥平面SCD ，因为SC ⊂平面SCD ，则BC SC ⊥，故SBC ∠为锐角，A 错；对于B 选项，因为SD ⊥平面ABCD ，AB ⊂平面ABCD ，则SD AB ⊥，B 对；对于C 选项，若SA ⊥平面ABCD ，且SD ⊥平面ABCD ，则SA 、SD 平行或重合，矛盾，假设不成立，C 错；对于D 选项，若//SA 平面SBC ，则SA 与平面SBC 无公共点，这与SA 平面SBC S =矛盾，假设不成立，D 错.故选：B.7．（2023·广东）已知α和β是两个不同平面，A ://αβ，B :α和β没有公共点，则A 是B 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】C【详解】两个平面平行的定义是：两个平面没有公共点，则这两个平面平行，因此A 是B 的充要条件．故选：C ．8．（2023春·新疆）已知直线a 和两个不重合的平面,αβ，则下列命题正确的是（）A ．若,a a αβ⊂∥，则αβ∥B ．若,a a αβ⊥⊥，则αβ⊥C ．若,a a αβ∥∥，则αβ∥D ．若,a a αβ⊥∥，则αβ⊥【答案】D【详解】若,a a αβ⊂∥，则,αβ不一定平行，还可以相交，故A 错误；若,a a αβ⊥⊥，则αβ∥，故B 错误；若,a a αβ∥∥，则,αβ不一定平行，还可以相交，故C 错误；若,a a αβ⊥∥，则必存在直线b α⊂，且//b a ，而a β⊥，所以b β⊥，所以αβ⊥，故D 正确.故选：D9．（2022·北京）在空间中，设,m n 是不同的直线，,αβ是不同的平面，则下形命题中真命题是（）A ．若//,//m n αα，则//m nB ．若,m n αα⊥⊥，则//m nC ．若//,//m m αβ，则//αβD ．若//,m m αβ⊂，则//αβ【答案】B【详解】若//,//m n αα，则//m n 或m 与n 相交或m 与n 是异面直线，故A 错误；若,m n αα⊥⊥，则//m n ，故B 正确；若//,//m m αβ，则//αβ或α与β相交，故C 错误；若//,m m αβ⊂，则//αβ或α与β相交，故D 错误.故选：B.10．（2022秋·广东）已知直线m 与平面α，则下列结论成立的是（）A ．若直线m 垂直于平面α内的一条直线，则m α⊥B ．若直线m 垂直于平面α内的两条直线，则m α⊥C ．若直线m 平行于平面α内的一条直线，则//m αD ．若直线m 与平面α没有公共点，则//m α【答案】D【详解】对于A 选项，若直线m 垂直于平面α内的一条直线，则//m α或m 与α相交（不一定垂直）或m α⊂，A 错；对于B 选项，若直线m 垂直于平面α内的两条直线，则m 与α的位置关系不确定，B 错；对于C 选项，若直线m 平行于平面α内的一条直线，则//m α或m α⊂，C 错；对于D 选项，若直线m 与平面α没有公共点，则//m α，D 对.故选：D.11．（2022春·广西）如图，正方体1111ABCD A B C D -中，,E F 分别是1111,B C D C 的中点，则下列结论正解的是（）A ．EF BD ⊥B ．EF BD ∥C ．EF 与BD 相交D ．EF 与11B D 相交【答案】B【详解】由,E F 分别是1111,B C D C 的中点可得11EF B D ∥，又易得11B D BD ∥，则EF BD ∥.12．（2022春·贵州）如图，在正方体1111ABCD A B C D -中，直线1A B 与1D C 的位置关系是（）A ．相交B ．平行C ．异面不垂直D ．异面垂直【答案】B【详解】在正方体1111ABCD A B C D -中，11//BC A D 且11BC A D =，所以四边形11BCD A 为平行四边形，所以11//A B D C .故选：B13．（2021秋·浙江）已知平面,αβ和直线l ，则下列说法正确的是（）A ．若//,//l l αβ，则//αβB ．若//,l l αβ⊂，则//αβC ．若,l l αβ⊥⊂，则αβ⊥D ．若,l l αβ⊥⊥，则αβ⊥【答案】C【详解】解：对于A 选项，若//,//l l αβ，则//αβ或相交，故A 选项不正确；对于B 选项，若//,l l αβ⊂，则//αβ或相交，故B 选项不正确；对于C 选项，若,l l αβ⊥⊂，则αβ⊥，为面面垂直的判定定理，故C 选项正确；对于D 选项，若,l l αβ⊥⊥，则//αβ，故D 选项不正确.故选：C.14．（2021春·贵州）如图，正方体1111ABCD A B C D -中，E 为1DD 的中点，则下列直线中与平面AEC 平行的是（）A ．1AD B ．1AA C ．1BD D ．EO【详解】解：对于A ，因为直线1AD 与平面AEC 交于点A ，故不平行；对于B ，因为直线1AA 与平面AEC 交于点A ，故不平行；对于C ，在正方体1111ABCD A B C D -中，因为E 为1DD 的中点，O 为BD 的中点，所以1EO BD ∕∕，又EO ⊂平面AEC ，1BD ⊄平面AEC ，所以1BD ∕∕平面AEC ；对于D ，因为EO ⊂平面AEC ，故不平行.故选：C.15．（2021秋·贵州）如图，在正方体ABCD -A 1B 1C 1D 1中，直线1BC 与平面DAA 1D 1的位置关系是（）A ．直线1BC 与平面11DAA D 平行B ．直线1BC 与平面11DAAD 垂直C ．直线1BC 与平面11DAAD 相交但不垂直D ．直线1BC 在平面11DAA D 【答案】A【详解】连接1AD ，由正方体的性质可得11//AB D C 且11AB D C =，所以11ABC D 为平行四边形，所以11//AD BC ，又因为1AD ⊂平面11DAA D ，1BC ⊄平面11DAA D ，所以1//BC 平面11DAA D ，故选：A16．（多选）（2021·湖北）已知l ，m 是平面α外的两条不同的直线，则下列命题中正确的是（）A ．若//l α，//m α，则//l mB ．若l α⊥，//m α，则l m ⊥C ．若l α⊥，l m ⊥，则//m αD ．若l m ⊥，//m α，则l α⊥【答案】BC【详解】解：对于A ，直线l 和m 可以相交或者异面，故A 错，对于B,//m α，假设//m n ，n ⊂α，又l α⊥，故l n ⊥，则l m ⊥，故B 对,对于C,因为l α⊥，l m ⊥，又m α⊄，则//m α，故C 对,对于D,直线l 可以与平面α平行，故D 错.故选：BC .17．（2023·北京）如图，在正方体1111ABCD A B C D -中，Ω是正方形ABCD 及其内部的点构成的集合．给出下列三个结论：①P ∀∈Ω，11A P A A ≥；②P ∃∈Ω，11A P B C ∥；③P ∀∈Ω，1A P 与1B C 不垂直．其中所有正确结论的序号是．【答案】①②③【详解】对于①，1A A ⊥平面ABCD ，∴∀∈ΩP ，11A P A A ≥，故①正确；对于②，当P 到达D 点时，11A P B C ∥，1111,// = DC A B A B DC ,11∴A B CD 是平行四边形，11∴A D B C ∥,11∴A P B C ∥,∴∃∈ΩP ，11A P B C ∥，故②正确；对于③，1111,,⊥⊥∴⊥ B C BC B C AB B C 平面11ABC D过1A 作平面11ABC D 的平行面11A B EF 与平面ABCD 的交线EF 在正方形ABCD 外，∴∀∈ΩP ，1A P 与1B C 不垂直,故③正确.故答案为：①②③.18．（2022春·广西）如图，在三棱锥P -ABC 中，PA ⊥底面ABC ，90ACB ∠=︒，则这个三棱锥的四个面中，是直角三角形的个数有个.【答案】4【详解】由于PA ⊥平面ABC ，所以,,PA AB PA AC PA BC ⊥⊥⊥，所以三角形PAB 和三角形PAC 是直角三角形.由于90ACB ∠=︒，所以BC AC ⊥，三角形ABC 是直角三角形.由于AC PA A ⋂=，所以BC ⊥平面PAC ，所以BC PC ⊥，所以三角形PBC 是直角三角形.所以三棱锥四个面中，是直角三角形的个数有4个.故答案为：419．（2021·北京）如图，在正方体1111-ABCD A B C D 中，E 是1BC 的中点.给出下列三个结论：①111//BC ADD A 平面；②1BC DE ⊥；③线段1BC 的长度大于线段DE 的长度.其中所有正确结论的序号是.【答案】①②③【详解】连接1AD 、BD 、1DC ，并设正方体的棱长为a .对于①，由于11//BC AD ，可知1//BC 平面11ADD A ，①正确；对于②，由于1BD DC =，又E 是1BC 的中点，易知1BC DE ⊥，②正确；对于③，BD 、1DC 、1BC 是正方体的面对角线，可知11BD DC BC ==，因此1BDC 是等边三角形，而DE 是等边三角形边上的高线，因此1||||BC DE >，③正确.故答案为：①②③考点三：异面直线所成角1．（2023春·湖南）如图，在正方体1111ABCD A B C D -中，异面直线AC 与11B D 所成的角为（）A ．6πB ．4πC ．3πD ．2π【答案】D【详解】由题意，正方体中得11//B D BD ，故异面直线AC 与11B D 所成的角，即正方形对角线AC 与BD 的夹角2π，故选：D2．（2023·云南）在正方体1111ABCD A B C D -中，异面直线AC 与1A D 所成角的大小为（）A ．π6B ．π4C ．π3D ．π2【答案】C【详解】连结1B C 、1AB ，如下图：在正方体1111ABCD A B C D -中，11//A B DC 且11A B DC =；∴四边形11A B CD 为平行四边形，则11//A D B C ；又 在正方体1111ABCD A B C D -中，1AB C 为等边三角形，∴1ACB ∠就是异面直线AC 与1A D 所成角,1π3ACB ∠=，∴异面直线AC 与1A D 所成角的大小为π3.故选：C.3．（2021春·河北）如图，在正方体1111ABCD A B C D -中，E F ，分别是AB ，1CC 的中点，则异面直线EF 与11AC 所成角的余弦值是（）A ．34B ．32C ．24D ．68【答案】B【详解】取BC 的中点M ，连接ME ，MF ．1111ABCD A B C D - 为正方体，11//AC AC ∴．又M ，E 分别是BC ，AB 的中点，//AC ME ∴，∴异面直线EF 与11AC 所成的角为FEM ∠．设正方体的棱长为2，1CC ⊥ 平面ABCD ，2,2,5EM BC CE === ，6EF ∴=,2,MF =2ME =，在FEM △中，222cos 2ME EF MF FEM ME EF +-∠=⋅26232226+-==⨯⨯．故选：B4．（2021秋·浙江）如图，正方体1111ABCD A B C D -中，,E F 分别为棱1111,C D A D 的中点，则异面直线DE 与AF 所成角的余弦值是（）A ．45B ．35C ．31010D ．1010【答案】A【详解】取11A B 的中点N ，连接,,EN FN AN由,E N 分别为1111,C D A B 的中点，则11//EN A D 且11EN A D =在正方体中11//AD A D 且11AD A D =,所以//EN AD 且EN AD=所以四边形ANED 为平行四边形，所以//AN DE则FAN ∠（或其补角）为异面直线DE 与AF 所成角.设正方体的棱长为2，则在ANF 中，11122NF D B ==,415AN AF ==+=所以2225524cos 25255AF AN FN FAN AF AN +-+-∠===⋅⨯⨯故选：A5．（2021春·福建）如图的正方体1111ABCD A B C D -中，异面直线1AA 与BC 所成的角是（）A ．30°B ．45°C ．60°D ．90°【答案】D【详解】在正方体1111ABCD A B C D -中，1AA ⊥平面ABCD ，BC ⊂平面ABCD ，1AA BC∴⊥异面直线1AA 与BC 所成的角是90︒.故选：D.考点四：直线与平面所成角1．（2023·江苏）如图，正方体1111ABCD A B C D -中，直线1BD 与平面ABCD 所成角的正切值为（）A ．1B ．32C ．22D ．33【答案】C 【详解】如图所示：连接BD ，因为1DD ⊥平面ABCD ，故1DBD ∠线1BD 与平面ABCD 所成角，设正方体棱长为1，则11,2DD DB ==，112tan 2DD DBD DB∴∠==.故选：C 2．（2022秋·浙江）如图，正方体1111ABCD A B C D -中，N 是棱1DD 的中点，则直线CN 与平面11DBB D 所成角的正弦值等于（）A ．12B ．105C ．155D ．2155【答案】B【详解】连接AC 、BD 交于O ,由正方形的性质可得CO BD ⊥，又1BB ⊥ 平面ABCD ，CO ⊂平面ABCD ，1BB CO ∴⊥，又1BB 与BD 在平面11DBB D 内相交，所以CO ⊥平面11DBB D CNO ∴∠是CN 与平面11DBB D 所成的角，设正方体的棱长为2，则5CN =，2CO =，210sin 55CO CNO CN ∴∠===，故选：B.3．（2021秋·浙江）如图，在三棱锥D ABC -中，AB BC CD DA ===，90,,,ABC E F O ︒∠=分别为棱,,BC DA AC 的中点，记直线EF 与平面BOD 所成角为θ，则θ的取值范围是（）A ．0,4π⎛⎫ ⎪⎝⎭B ．,43ππ⎛⎫ ⎪⎝⎭C ．,42ππ⎛⎫ ⎪⎝⎭D ．,62ππ⎛⎫ ⎪⎝⎭【答案】C 【详解】由AB BC =，90ABC ︒∠=，将底面补全为正方形ABCG ，如下图示，O 为ABCG 对角线交点且GB AC ⊥，又CD DA =有DO AC ⊥，DO GB O ⋂=，∴AC ⊥面GDB ，而AC ⊂面ABCG ，故面GDB ⊥面ABCG ，若H 为DG 的中点，连接FH ，又,E F 为棱,BC DA 的中点，则//FH AG 且2AG FH =，而//BC AG ，2BC AG EC ==，有,EC FH 平行且相等，即ECHF 为平行四边形.∴可将EF 平移至HC ，直线EF 与平面BOD 所成角为(0,)2CHO πθ∠=∈，且Rt CHO △中90COH ∠=︒，令2AB BC CD DA ====，2OC =，即2222tan tan OC BD OH θθ===，∴△ABD 中，2222cos AB BD AB BD DAB BD +-⋅⋅∠=，即21cos 1tan DAB θ∠=-，∵DAB DAG DCB DCG ≅≅≅ ，即(0,)2DAB π∠∈，∴21011tan θ<-<，解得tan 1θ>（tan 1θ<-舍去），综上有(,)42ππθ∈，故选：C4．（2021秋·贵州）如图，在三棱锥-P ABC 中，PA ⊥底面ABC ，PA AC =，则直线PC 与平面ABC 所成角的大小为A ．30B ．45C ．60D ．90【答案】B 【详解】由题意可知，PA ⊥底面ABC ，所以PCA ∠为直线PC 与平面ABC 所成角，PA AC =，所以三角形PCA 为等腰直角三角形，所以PCA 45∠= ，故选B考点五：二面角1．（2023·河北）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，PCD 是等边三角形，平面PCD ⊥底面ABCD ，3AD =，四棱锥P ABCD -的体积为183，E 为PC 的中点．平面PAB 与平面ABCD 所成二面角的正切值是（）A ．2B ．3C ．2D ．1【答案】B 【详解】分别取,CD AB 的中点为,G F ，连接,,,,G P FG P AG F B G ，设()2,0CD a a =>，则3PG a =.因为PCD 是等边三角形，所以PG CD ⊥，又因为平面PCD ⊥平面ABCD ，平面PCD 平面ABCD CD =，PG ⊂平面PCD ，PG ⊥底面ABCD ，因为四棱锥P ABCD -的体积为183，所以1(32)31833a a ⨯⨯=，解得3a =.则PG FG ⊥，,PG AG PG BG ⊥⊥，所以PA PB =，PF AB ⊥，又因为底面ABCD 为矩形，所以FG AB ⊥，所以PFG ∠为平面PAB 与平面ABCD 所成二面角的平面角，33tan 33PG PFG FG∠===.故选：B考点六：立体几何解答题1．（2023·北京）阅读下面题目及其解答过程．如图，在直三棱柱111ABC A B C -中，AB AC ⊥，D ，E 分别为BC ，11A B 的中点．（1）求证：//DE 平面11A ACC ；（2）求证：AB DE ⊥．解：（1）取11AC 的中点F ，连接EF ，FC ，如图所示．在111A B C △中，E ，F 分别为11A B ，11AC 的中点，所以11//EF B C ，1112EF B C =．由题意知，四边形11B BCC 为①．因为D 为BC 的中点，所以11//DC B C ，1112DC B C =．所以//EF DC ，EF DC =．所以四边形DCFE 为平行四边形，所以//DE CF ．又②，CF ⊂平面11A ACC ，所以，//DE 平面11A ACC ．（2）因为111ABC A B C -为直三棱柱，所以1A A ⊥平面ABC ．又AB ⊂平面ABC ，所以③．因为AB AC ⊥，且1A A AC A =I ，所以④．又CF ⊂平面11A ACC ，所以AB CF ⊥．因为⑤，所以AB DE ⊥．以上题目的解答过程中，设置了①~⑤五个空格，如下的表格中为每个空格给出了两个选项，其中只有一个符合逻辑推理．请选出符合逻辑推理的选项，并填写在答题卡的指定位置（只需填写“A”或“B”）．空格序号选项①A ．矩形B ．梯形②A ．DE ⊄平面11A ACCB ．DE ⊂平面11A ACC ③A ．1BC A A ⊥B ．1AB A A ⊥④A ．AB ⊥平面11A ACC B ．BC ⊥平面11A ACC ⑤A ．DE CF =B ．//DE CF【答案】（1）①A ；②A ；（2）③B ；④A ；⑤B【详解】①根据直棱柱的结构特征及给定的条件知：结论为四边形11B BCC 为矩形，填A ；②由线面平行的判定条件，条件中缺DE ⊄平面11A ACC ，填A ；③由线面垂直的性质知：结论为1AB A A ⊥，填B ；④由线面垂直的判定知：结论为AB ⊥平面11A ACC ，填A ；⑤根据AB CF ⊥及所得结论为AB DE ⊥，条件应为//DE CF ，填B.故答案为：A ，A ，B ，A ，B2．（2023·山西）如图所示，三棱柱111ABC A B C -，底面是边长为2的正三角形，侧棱1AA ⊥底面ABC ，点,E F 分别是棱1CC ，1BB 上的点，点M 是线段AC 的中点，22EC FB ==．(1)求证//BM 平面AEF ；(2)求BM 与EF 所成角的余弦值．【答案】(1)证明见解析；(2)BM 与EF 所成角的余弦值为155.【详解】（1）取AE 的中点O ，连接,OF OM ，∵,O M 分别为,AE AC 的中点，∴//OM CE ，12OM EC =，由//BF CE ，且22EC FB ==，∴//OM FB ，且OM FB =，∴四边形OMBF 为平行四边形，故//BM OF ，又BM ⊄平面AEF ，OF ⊂平面AEF ，∴//BM 平面AEF ；（2）因为//BM OF ，所以EFO ∠为直线BM 与EF 所成角，Rt ABF 中，2222215AF AB FB =+=+=，直角梯形BCEF 中，2,2,1,90EC BC BF CBF BCE ===∠=∠=o ，过F 作FG CE ⊥，G 为垂足，如图所示，则1BF CG ==，2FG BC ==，1GE =，2222125EF GE FG =+=+=，AF EF =，所以AEF △为等腰三角形，则FO AE ⊥，Rt ACE 中，22222222AE AC CE =+=+=，所以2AO EO ==，Rt AOF 中，()()2222523FO AF AO =-=-=，所以315cos 55FO EFO EF ∠===所以BM 与EF 所成角的余弦值为155.3．（2023·江苏）如图，三棱锥-P ABC 的底面ABC 和侧面PBC 都是边长为2的等边三角形，,M N 分别是,AB BC 的中点，PN AN ⊥.(1)证明：MN //平面PAC ；(2)求三棱锥-P ABC 的体积.【答案】(1)证明见解析(2)1【详解】（1）因为,M N 分别是,AB BC 的中点，所以//MN AC ，因为MN ⊄平面PAC ，AC ⊂平面PAC ，所以MN //平面PAC ；（2）因为PBC 是等边三角形，N 是BC 的中点，所以PN BC ⊥，因为PN AN ⊥，,AN BC ⊂平面ABC ，,AN BC N ⋂=所以PN ^平面ABC ，因为底面ABC 和侧面PBC 都是边长为2的等边三角形，所以1132231334P ABC ABC V S PN -=⨯=⨯⨯⨯⨯= 4．（2023春·福建）如图，长方体1111ABCD A B C D -，2AB =，11BC CC ==.(1)求三棱锥1C BCD -的体积；(2)证明：11//B D 平面1C BD .【答案】(1)13(2)证明见解析【详解】（1）解：在长方体1111ABCD A B C D -中，1CC ⊥平面ABCD ，且BC CD ⊥，因为2AB =，11BC CC ==，则2CD AB ==，1112122BCD S BC CD =⋅=⨯⨯=△，因此，三棱锥1C BCD -的体积为1111111333C BCD BCD V S CC -=⋅=⨯⨯=△.（2）证明：在长方体1111ABCD A B C D -中，11//BB DD 且11BB DD =，所以，四边形11BB D D 为平行四边形，则11//B D BD ，因为11B D ⊄平面1C BD ，BD ⊂平面1C BD ，因此，11//B D 平面1C BD .5．（2023春·湖南）如图，P 为圆锥的顶点，O 为底面圆的圆心，AC 为底面圆的直径，B 是底面圆周上不同于A ，C 的任意一点，点D ，E 分别为母线PB ，PC 的中点.(1)求证：//DE 平面ABC ；(2)若2PO =，2AB BC ==，求圆锥PO 的体积.【答案】(1)见解析(2)2π3【详解】（1）由于D ，E 分别为母线PB ，PC 的中点,所以//DE BC ,由于DE ⊄平面ABC ,BC ⊂平面ABC ,所以//DE 平面ABC（2）AC 为底面圆的直径，B 是底面圆周上不同于A ，C 的任意一点，所以AB CB ⊥,又2AB BC ==，所以222AC AB BC =+=,因此底面圆的半径为112AC =,故圆锥PO 的体积为212ππ1233⨯⨯=，6．（2023·广东）如图，圆的直径为AB =4，直线PA 垂直圆所在的平面，C 是圆上的任意一点.(1)证明BC ⊥面PAC ；(2)若22,2,PA AC ==求PB 与面PAC 的夹角.【答案】(1)证明见解析；(2)45︒．【详解】（1）证明：PA ⊥平面ABC ，BC ⊂平面ABC ，∴PA BC ⊥，同理PA AC ⊥，AB 是圆直径，C 在圆周上，因此AC BC ⊥，又PA AC A = ，,PA AC ⊂平面PAC ，∴BC ⊥平面PAC ；（2）由（1）BC ⊥平面PAC ，∴BPC ∠是PB 与平面PAC 所成的角，又PC ⊂平面PAC ，∴BC PC ⊥，由已知2223PC PA AC =+=，224223BC =-=，所以45BPC ∠=︒，∴PB 与平面PAC 所成的角是45︒．7．（2023·云南）如图，四棱锥S ABCD -的底面是边长为1的正方形，SD ⊥平面,2ABCD SD =.(1)求四棱锥S ABCD -的体积；(2)求证：AC ⊥平面SBD .【答案】(1)23(2)证明见详解【详解】（1）已知四棱锥S ABCD -的底面是边长为1的正方形，由SD ⊥平面ABCD 得四棱锥S ABCD -的高为SD ，所以四棱锥S ABCD -的体积11212333V S SD =⨯=⨯⨯=底；（2）因为四棱锥S ABCD -的底面是正方形，所以AC BD ⊥,因为SD ⊥平面ABCD ，AC ⊂平面ABCD ，所以SD AC ⊥，又SD BD D = ，SD ⊂平面SBD ，BD ⊂平面SBD ，所以AC ⊥平面SBD .8．（2023春·新疆）在三棱锥-P ABC 中，PA ⊥底面ABC ，AB BC ⊥，E ，F 分别是BC ，PC 的中点．(1)证明：//EF 平面PAB ；(2)证明EF BC ⊥．【答案】(1)证明见解析(2)证明见解析【详解】（1）在PBC 中，因为E ，F 分别是BC ，PC 的中点，则//EF PB ，因为EF ⊄平面PAB ，BP ⊂平面PAB ，所以//EF 平面PAB ．（2）因为PA ⊥底面ABC ，BC ⊂平面ABC ，则PA BC ⊥，又,,,AB BC PA AB A PA AB ⊥=⊂I 平面PAB ，因此BC ⊥平面PAB ，而BP ⊂平面PAB ，于是BC PB ⊥，由（1）知//EF PB ，所以EF BC ⊥.9．（2022·北京）阅读下面题目及其解答过程．如图，已知正方体1111ABCD A B C D -．（Ⅰ）求证：1AC BD ⊥；（Ⅱ）求证：直线1D D 与平面1AB C 不平行．解：（Ⅰ）如图，连接11,BD B D ．因为1111ABCD A B C D -为正方体，所以1D D ⊥平面ABCD ．所以①___________．因为四边形ABCD 为正方形，所以②__________．因为1D D BD D ⋂=，所以③____________．所以1AC BD ⊥．（Ⅱ）如图，设AC BD O = ，连接1B O ．假设1//D D 平面1AB C ．因为1D D ⊂平面11D DBB ，且平面1AB C 平面11D DBB =④____________，所以⑤__________．又11//D D B B ，这样过点1B 有两条直线11,B O B B 都与1D D 平行，显然不可能．所以直线1D D 与平面1AB C 不平行．以上题目的解答过程中，设置了①~⑤五个空格，如下的表格中为每个空格给出了两个选项，其中只有一个符合推理，请选出符合推理的选项，并填写在答题卡的指定位置（只需填写“A”或“B”）．空格序号选项①A ．1D D AC ⊥B ．1D D BD ⊥②A ．AB BC ⊥B ．AC BD ⊥③A ．1BD ⊥平面1ABC B ．AC ⊥平面11D DBB ④A ．1B O B ．1B B ⑤A ．11//D D B O B ．1D D 与1B O 为相交直线【答案】（Ⅰ）①A ②B ③B ；（Ⅱ）④A ⑤A【详解】要证明1AC BD ⊥，可通过证明AC ⊥平面11D DBB 来证得，要证明AC ⊥平面11D DBB ，可通过证明1,D AC A BD D C ⊥⊥来证得，所以①填A ，②填B ，③填B.平面1AB C 与平面11D DBB 的交线为1B O ，所以④填A ，由于1//D D 平面1AB C ，因为1D D ⊂平面11D DBB ，且平面1AB C 平面111D DBB B O =，根据线面平行的性质定理可知，11//D D B O ，所以⑤填A.10．（2022秋·广东）如图，PA 是圆柱的母线，AB 是底面圆的直径，C 是底面圆周上异于A ．B 的一点，且2PA AC BC ===．(1)求证：BC ⊥平面PAC(2)若M 是PC 的中点，求三棱锥B ACM -的体积．【答案】(1)证明见解析(2)23【详解】（1）∵PA 为圆柱母线，∴PA ⊥平面ACB ，∵BC ⊂平面ACB ，∴PA BC ⊥，∵AB 为底面圆直径，∴BC AC ⊥，∵AC ⊂平面APC ，PA ⊂平面APC ，AC PA A ⋂=，∴BC ⊥平面PAC.（2）∵BC ⊥平面APC ，平面AMC =平面APC ，∴BC ⊥平面ACM ，BC 为三棱锥B ACM -的高，=2BC ，∵2AC PA ==，M 为PC 中点，∴AM PC ⊥，==2AM MC ，1=22=12ACM S ⨯⨯ ，∴12=12=33B ACM V -⨯⨯.11．（2022秋·福建）如图，在三棱锥-P ABC 中，平面PAC ⊥平面,ABC AC BC⊥(1)求证：PA ⊥BC ；(2)若2,30PA PC BC BAC ∠==== ，求三棱锥-P ABC 的体积.【答案】(1)证明见解析(2)233【详解】（1）证明：因为平面PAC ⊥平面,ABC AC BC ⊥，平面PAC 平面ABC AC =，BC ⊂平面ABC ，所以BC ⊥平面PAC ，又PA ⊂平面PAC ，所以PA ⊥BC ；（2）解：由（1）知BC ⊥平面PAC ，所以BC AC ⊥，又2,30BC BAC ∠== ，所以23AC =，因为2PA PC ==，所以()22222231cos 2222APC +-∠==-⨯⨯，所以23sin 1cos 2APC APC ∠=-∠=，所以1322322APC S =⨯⨯⨯= ，所以三棱锥-P ABC 的体积113233233A AP B C P C V S BC -⨯=⨯==⨯ .12．（2022春·天津）如图，四棱锥P ABCD -的底面是正方形，PD ⊥平面ABCD ，M ，N 分别是BC ，PC 的中点.(1)求证：//MN 平面PDB ；(2)求证：AC ⊥平面PDB .【答案】(1)证明见解析(2)证明见解析【详解】（1）因为M ，N 分别是BC ，PC 的中点，故MN PB ∥.又PB ⊂平面PDB ，MN ⊄平面PDB ，故//MN 平面PDB.（2）因为PD ⊥平面ABCD ，且AC ⊂平面ABCD ，故AC PD ⊥.又因为四棱锥P ABCD -的底面是正方形，则AC BD ⊥.又BD PD D = ，,BD PD ⊂平面PDB ，故AC ⊥平面PDB.13．（2022·山西）如图，在直四棱柱1111ABCD A B C D -中，底面ABCD 为菱形，E 为1DD 中点.（1）求证：1//BD 平面ACE ；（2）求证：1BD AC ⊥.【答案】（1）证明见解析；（2）证明见解析；【详解】证明：（1）设AC 与BD 交于点O ，接OE ，底面ABCD 是菱形，O ∴为DB 中点，又因为E 是1DD 的中点，1//OE D BB ∴，OE ⊂ 面AEC ，1BD ⊂平面AEC1//BD ∴平面ACE ．（2） 底面ABCD 是菱形，AC BD ∴⊥，1DD ⊥Q 底面ABCD ，AC ⊂底面ABCD ，1DD AC ∴⊥，且1DB DD D = ，1,DB DD ⊂平面11BDB D ．AC ∴⊥平面11BDB D ．1BD ⊂ 平面11BDB D ，1AC BD ∴⊥．14．（2022春·浙江）如图，在四棱锥P ABCD -中，底面ABCD 是梯形，,AB CD AD AB ⊥∥，1,2AB AD PD CD PD ===⊥平面ABCD ，点M 是棱PC 上的一点．(1)若3PC PM =，求证：PA 平面MBD ；(2)若M 是PC 的中点，求二面角M BD C --的余弦值．【答案】(1)证明见解析(2)63【详解】（1）证明：连接AC 交BD 于N ，连接MN ，因为AB ∥CD所以ANB ∽CND △，所以12AN ABNC DC ==，因为12PM MC =，所以12AN PMNC MC ==,所以PA ∥MN ,因为PA ⊄平面,MBD MN ⊂平面MBD所以PA ∥平面MBD（2）过M 作ME DC ⊥于E ，因为PD ⊥平面ABCD ，PD ⊂平面PDC ，所以平面PDC ⊥平面ABCD ，因为平面PDC 平面ABCD CD =，所以ME ⊥平面ABCD ，因为BD ⊂平面ABCD ，所以ME BD⊥过E 作EF BD ⊥于F ，连接MF ，因为ME EF E ⋂=，所以BD ⊥平面MEF ，因为MF ⊂平面MEF ，所以,MF BD ⊥所以MFE ∠是二面角M BD C --的平面角，不妨设2AB =，则122AB AD PD CD ====，因为,AB CD AD AB ⊥∥，所以22,22,4BD BC DC ===，所以222BD BC DC +=，所以BD BC ⊥，所以111,222ME PD EF BC ====，所以3MF =，所以6cos 3EFMFE MF ∠==15．（2022·湖南）在直三棱柱111ABC A B C -中，AB AC =，D 为BC 中点.(1)求证：AD ⊥平面11BCC B ；(2)若12,3AB BC AA ===，求四棱锥11A BCC B -的体积.【答案】(1)证明见解析；(2)23.【详解】（1）AB AC = ，D 为BC 中点，AD BC ∴⊥,在直三棱锥111ABC A B C -中，1B B ⊥平面ABC ,AD ⊂平面ABC .1B B AD ∴⊥，又1BC B B B =∩,AD ∴⊥平面11BCC B （2）2AB AC BC === ，D 为BC 中点，3232AD ∴=⨯=，由（1）知，四棱锥11A BCC B -的高即为3AD =，又13AA =，所以111326B BCC S B B BC =⋅=⨯=矩形，11632333V S h ∴=⋅=⨯⨯=.16．（2022春·广西）如图，AB 是底面O 的直径，C 为O 上异于A 、B 的点，PC 垂直于O 所在平面，D 、E 分别为PA 、PC 的中点.(1)求证：DE ∥平面ABC .(2)求证：平面BDE ⊥平面PBC .【答案】(1)证明详见解析(2)证明详见解析【详解】（1）由于,D E 分别是,PA PC 的中点，所以//DE AC ，由于DE ⊂/平面,ABC AC ⊂平面ABC ，所以//DE 平面ABC .（2）依题意PC ⊥平面ABC ，所以PC AC ⊥.由于AB 是圆O 的直径，所以AC BC ⊥,由于PC BC C ⋂=，所以AC ⊥平面PBC ，由于//DE AC ，所以DE ⊥平面PBC ，由于DE ⊂平面BDE ，所以平面BDE ⊥平面PBC .17．（2022春·贵州）如图，直三棱柱111ABC A B C -中，12,2,AB BC CC AB BC ===⊥，M 为棱1CC 上一点．(1)求三棱锥111C A B C -的体积；(2)求证：11A B BM ⊥．【答案】(1)23；(2)证明见解析（1）由直三棱柱111ABC A B C -可得1CC ⊥平面111A B C ，又2,AB BC AB BC ==⊥，可得111111112,A B B C A B B C ==⊥，则111111111122223323C A B C A B C V S CC -=⋅=⨯⨯⨯⨯= ；（2）由题意得，1CC ⊥平面111A B C ，11A B ⊂平面111A B C ，则111CC A B ⊥，又1111A B B C ⊥，1111B C CC C ⋂=，111,B C CC ⊂平面11BCC B ，则11A B ⊥平面11BCC B ，又BM ⊂平面11BCC B ，则11A B BM ⊥.18．（2021·北京）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，PD ⊥平面ABCD .(1)求证：//BC 平面PAD ；(2)求证：AC ⊥平面PBD .【答案】(1)证明见解析(2)证明见解析【详解】（1）由底面ABCD 是正方形，//BC AD∴又BC ⊄平面PAD ，AD ⊂平面PAD ，//BC ∴平面PAD（2）PD ⊥ 平面ABCD ，AC ⊂平面ABCD ，PD AC∴⊥又底面ABCD 是正方形，BD AC∴⊥又BD PD D = ，,BD PD ⊂平面PBD ，AC ∴⊥平面PBD19．（2021春·天津）如图，长方体1111ABCD A B C D -中，底面ABCD 是正方形．(1)求证：11//B D 平面1BDC ；(2)求证：11B D ⊥平面11ACC A ．【答案】(1)证明见解析(2)证明见解析【详解】（1）在长方体1111ABCD A B C D -中，11//BB DD 且11BB DD =，所以四边形11BB D D 为平行四边形，所以11//BD B D ，因为11B D ⊄平面1BDC ，BD ⊂平面1BDC ，所以11//B D 平面1BDC .（2）因为底面ABCD 是正方形，所以AC BD ⊥，又11//BD B D ，所以11B D AC ⊥，又1AA ⊥平面1111D C B A ，11B D ⊂平面1111D C B A ，所以111⊥B D AA ，又1AC AA A =∩，1,AC AA ⊂平面11ACC A ，所以11B D ⊥平面11ACC A .20．（2021秋·吉林）如图，三棱柱111ABC A B C -中，1AA ⊥平面ABC ，AB =3，AC =4，BC =5.(1)求证：AB ⊥平面11ACC A ；(2)若异面直线1BB 与1AC 所成的角为30°，求三棱柱111ABC A B C -的体积.【答案】(1)证明见解析(2)243【详解】（1）1AA ⊥平面ABC ，AB ⊂平面ABC ，有1AA AB ⊥.AB =3，AC =4，BC =5，有222AB AC BC +=，由勾股定理得AC AB ⊥.1AA AC A = ，1,AA AC ⊂平面11ACC A ，∴AB ⊥平面11ACC A （2）由11//BB AA ，异面直线1BB 与1AC 所成的角即为1∠AA C ，130AA C ∠= ，又1AA ⊥平面ABC ，AC ⊂平面ABC ，∴1AA AC ⊥，则1tan 30ACAA = ，得143AA =，1134622ABC S AB AC =⋅=⨯⨯=△，所以三棱柱111ABC A B C -的体积1643243ABC V S AA =⋅=⨯= .21．（2021·吉林）如图，在正方体1111ABCD A B C D -中，E 、F 分别为1DD ､1CC 的中点.（1）求证：1AC BD ⊥；（2）求证：//AE 平面1BFD .【答案】（1）证明见解析；（2）证明见解析.【详解】证明：（1）连结BD ，由正方体1111ABCD A B C D -得，1D D ⊥平面ABCD .又AC ⊂平面ABCD ，1AC D D∴⊥又四边形ABCD 是正方形，∴AC BD ⊥，而1D D BD D ⋂=，∴AC ⊥平面1BDD ，又1BD ⊂平面1BDD ，∴1AC BD ⊥.（2）连结EF ，由E ､F 分别为1111ABCD A B C D -､1111ABCD A B C D -的中点得，//EF AB 且EF AB=∴四边形ABFE 是平行四边形，∴//AE BF又AE ⊄平面1BFD ，BF ⊂平面1BFD ，∴//AE 平面1BFD .22．（2021春·福建）如图，在三棱锥-P ABC 中，E ，F 分别是AB ，AP 的中点.(1)求证：//EF 平面PBC ；(2)若三棱锥-P ABC 的各棱长均为2，求它的表面积.【答案】(1)证明过程见解析；(2)43【详解】（1）因为E ，F 分别是AB ，AP 的中点，所以EF 是三角形ABP 的中位线，所以EF //PB ，因为EF ⊄平面PBC ，PB ⊂平面PBC ，所以//EF 平面PBC .（2）若三棱锥-P ABC 的各棱长均为2，则该三棱锥为正四面体，四个面是全等的等边三角形，故它的表面积为2342434⨯⨯=23．（2021秋·福建）如图，在三棱锥-P ABC 中，已知△ABC 和△PBC 均为正三角形，D 为BC 的中点．。

会考逐题突破II -15 立体几何大题考情：①历年会考中都必考一题。

②两个关系：线面平行；线面垂直（异面直线垂直）； ③两个角：异面直线所成的角，直线与平面所成的角。

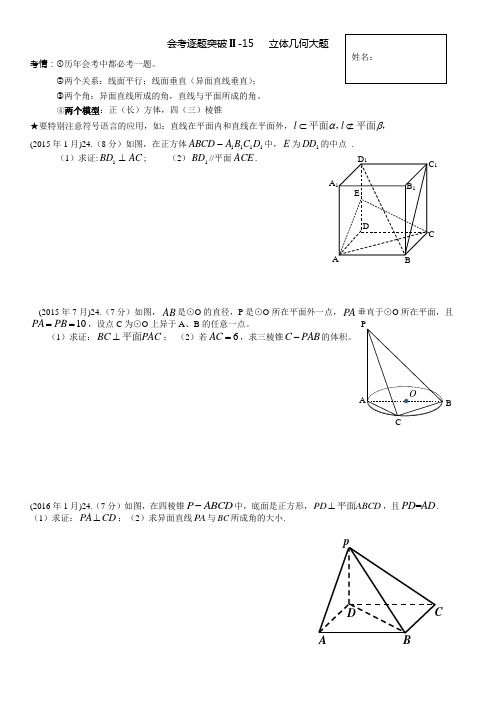
④两个模型：正（长）方体，四（三）棱锥★要特别注意符号语言的应用，如：直线在平面内和直线在平面外， l l αβ⊂⊄平面，平面，(2015年1月)24.（8分）如图，在正方体1111D C B A ABCD -中，E 为1DD 的中点 .（1）求证:AC BD ⊥1; （2）1BD //平面ACE .(2015年7月)24.（7分）如图，AB 是⊙O 的直径，P 是⊙O 所在平面外一点，PA 垂直于⊙O 所在平面，且10PA PB ==，设点C 为⊙O 上异于A 、B 的任意一点。

（1）求证：BC PAC ⊥平面； （2）若6AC =，求三棱锥C PAB -的体积。

(2016年1月)24.（7分）如图，在四棱锥P ABCD -中，底面是正方形，PD ABCD ⊥平面，且=PD AD . （1）求证：PA CD ⊥；（2）求异面直线PA 与BC 所成角的大小.姓名：pABCD BCA P OE ABC C 1DD 1A 1B 1NMD BCAPE(2016年7月)24.（7分）如图，在正方体1111D C B A ABCD -中，点E 、F 分别是棱AB AD 、的中点. (1)求证：EF //平面11D CB (2)求证：平面11C CAA ⊥平面11D CB(2017年1月)25.(6分）如图，四棱锥ABCD P -的底面ABCD 是平行四边形，E 为PA 的中点， （1）求证：PC//平面EBD（2）若⊥PA 底面ABCD ，且2,5,1,32====BD AB AD PA ，求点A 到平面EBD 的距离(2017年7月)25.（7分）四棱锥ABCD P -中，底面ABCD 是矩形，PA ABCD ⊥底面，,M N 分别是,PB PD的中点，2,3,4AB AD PA ===，E 为棱CD 上一点。

A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。

（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。

（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。

高考专题突破四高考中的立体几何问题【考点自测】1．在正三棱柱ABC－A1B1C1中，D为BC的中点，E为A1C1的中点，则DE与平面A1B1BA 的位置关系为()A．相交B．平行C．垂直相交D．不确定答案 B解析如图取B1C1的中点为F，连接EF，DF，则EF∥A1B1，DF∥B1B，且EF∩DF＝F，A1B1∩B1B＝B1，∴平面EFD∥平面A1B1BA，∴DE∥平面A1B1BA.2．设x，y，z是空间中不同的直线或平面，对下列四种情形：①x，y，z均为直线；②x，y是直线，z是平面；③z是直线，x，y是平面；④x，y，z均为平面．其中使“x⊥z且y⊥z⇒x∥y”为真命题的是()A．③④B．①③C．②③D．①②答案 C解析由正方体模型可知①④为假命题；由线面垂直的性质定理可知②③为真命题．3．(2018届黑龙江海林市朝鲜中学模拟)已知某几何体的三视图如图所示，则该几何体的表面积为()A．9＋4(2＋5) B．10＋2(2＋3)C．11＋2(2＋5) D．11＋2(2＋3)答案 C解析根据三视图还原几何体为一个直四棱柱，两底面为四边形(左视图)，其余各侧面为矩形，两底面面积为2⎝⎛⎭⎫12×2×2＋12×1×1＝5，四个侧面面积为2×2＋1×2＋2×5＋2×2＝6＋25＋22，几何体的表面积为11＋2(5＋2)，故选C.4．(2017·天津滨海新区模拟)如图，以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕，把△ABD 和△ACD 折成互相垂直的两个平面后，某学生得出下列四个结论：①BD ⊥AC ；②△BAC 是等边三角形； ③三棱锥D －ABC 是正三棱锥； ④平面ADC ⊥平面ABC . 其中正确的是( ) A ．①②④ B ．①②③ C ．②③④ D ．①③④答案 B解析 由题意知，BD ⊥平面ADC ，故BD ⊥AC ，①正确；AD 为等腰直角三角形斜边BC 上的高，平面ABD ⊥平面ACD ，所以AB ＝AC ＝BC ，△BAC 是等边三角形，②正确；易知DA ＝DB ＝DC ，又由②知③正确；由①知④错．故选B.5．(2017·沈阳调研)设α，β，γ是三个平面，a ，b 是两条不同的直线，有下列三个条件： ①a ∥γ，b ⊂β；②a ∥γ，b ∥β；③b ∥β，a ⊂γ.如果命题“α∩β＝a ，b ⊂γ，且________，则a ∥b ”为真命题，则可以在横线处填入的条件是________．(把所有正确的序号填上) 答案 ①或③解析 由线面平行的性质定理可知，①正确；当b ∥β，a ⊂γ时，a 和b 在同一平面内，且没有公共点，所以平行，③正确．故应填入的条件为①或③.题型一 求空间几何体的表面积与体积例1 (2016·全国Ⅱ)如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H ，将△DEF 沿EF 折到△D ′EF 的位置．(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′ABCFE 的体积．(1)证明 由已知得AC ⊥BD ，AD ＝CD ，又由AE ＝CF 得AE AD ＝CFCD，故AC ∥EF ，由此得EF ⊥HD ，折后EF 与HD 保持垂直关系，即EF ⊥HD ′，所以AC ⊥HD ′. (2)解 由EF ∥AC 得OH DO ＝AE AD ＝14.由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4， 所以OH ＝1，D ′H ＝DH ＝3，于是OD ′2＋OH 2＝(22)2＋12＝9＝D ′H 2， 故OD ′⊥OH .由(1)知AC ⊥HD ′，又AC ⊥BD ，BD ∩HD ′＝H ， BD ，HD ′⊂平面BHD ′，所以AC ⊥平面BHD ′，于是AC ⊥OD ′，又由OD ′⊥OH ，AC ∩OH ＝O ，AC ，OH ⊂平面ABC ， 所以OD ′⊥平面ABC . 又由EF AC ＝DH DO 得EF ＝92.五边形ABCFE 的面积S ＝12×6×8－12×92×3＝694.所以五棱锥D ′ABCFE 的体积 V ＝13×694×22＝2322.思维升华 (1)若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，等积转换法多用来求三棱锥的体积．(2)若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解．(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解． 跟踪训练1 (2018·乌鲁木齐质检)正三棱锥的高为1，底面边长为26，内有一个球与它的四个面都相切(如图)．求：(1)这个正三棱锥的表面积；(2)这个正三棱锥内切球的表面积与体积．解 (1)底面正三角形中心到一边的距离为13×32×26＝2，则正棱锥侧面的斜高为12＋(2)2＝3，∴S 侧＝3×12×26×3＝92，∴S 表＝S 侧＋S 底＝92＋12×32×(26)2＝92＋6 3.(2)设正三棱锥P －ABC 的内切球球心为O ，连接OP ，OA ，OB ，OC ，而O 点到三棱锥的四个面的距离都为球的半径r .∴V 三棱锥P －ABC ＝V 三棱锥O －P AB ＋V 三棱锥O －PBC ＋V 三棱锥O －P AC ＋V 三棱锥O －ABC ＝13S 侧·r ＋13S △ABC ·r ＝13S 表·r ＝(32＋23)r .又V P －ABC ＝13×12×32×(26)2×1＝23，∴(32＋23)r ＝23，得r ＝2332＋23＝23(32－23)18－12＝6－2.∴S 内切球＝4π(6－2)2＝(40－166)π. V 内切球＝43π(6－2)3＝83(96－22)π.题型二 空间点、线、面的位置关系例2 (2017·广州五校联考)如图，在四棱锥P －ABCD 中，底面ABCD 是菱形，P A ＝PD ，∠BAD ＝60°，E 是AD 的中点，点Q 在侧棱PC 上．(1)求证：AD ⊥平面PBE ；(2)若Q 是PC 的中点，求证：P A ∥平面BDQ ；(3)若V P－BCDE＝2V Q－ABCD，试求CPCQ的值．(1)证明由E是AD的中点，P A＝PD可得AD⊥PE.因为底面ABCD是菱形，∠BAD＝60°，所以AB＝BD，所以AD⊥BE，又PE∩BE＝E，PE，BE⊂平面PBE，所以AD⊥平面PBE.(2)证明连接AC，交BD于点O，连接OQ.因为O是AC的中点，Q是PC的中点，所以OQ∥P A，又P A⊄平面BDQ，OQ⊂平面BDQ，所以P A∥平面BDQ.(3)解设四棱锥P－BCDE，Q－ABCD的高分别为h1，h2.所以V四棱锥P－BCDE＝13S四边形BCDE h1，V四棱锥Q－ABCD＝13S四边形ABCD h2.又V P－BCDE＝2V Q－ABCD，且S四边形BCDE＝34S四边形ABCD，所以CPCQ＝h1h2＝83.思维升华(1)平行问题的转化利用线线平行、线面平行、面面平行的相互转化解决平行关系的判定问题时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而应用性质定理时，其顺序正好相反．在实际的解题过程中，判定定理和性质定理一般要相互结合，灵活运用．(2)垂直问题的转化在空间垂直关系中，线面垂直是核心，已知线面垂直，既可为证明线线垂直提供依据，又可为利用判定定理证明面面垂直作好铺垫．应用面面垂直的性质定理时，一般需作辅助线，基本作法是过其中一个平面内一点作交线的垂线，从而把面面垂直问题转化为线面垂直问题，进而可转化为线线垂直问题．跟踪训练2 如图，在直三棱柱ABC—A1B1C1中，AB＝AC，E是BC的中点，求证：(1)平面AB1E⊥平面B1BCC1；(2)A1C∥平面AB1E.证明(1)在直三棱柱ABC—A1B1C1中，CC1⊥平面ABC.因为AE⊂平面ABC，所以CC1⊥AE.因为AB＝AC，E为BC的中点，所以AE⊥BC.因为BC⊂平面B1BCC1，CC1⊂平面B1BCC1，且BC∩CC1＝C，所以AE⊥平面B1BCC1.因为AE⊂平面AB1E，所以平面AB1E⊥平面B1BCC1.(2)连接A1B，设A1B∩AB1＝F，连接EF.在直三棱柱ABC—A1B1C1中，四边形AA1B1B为平行四边形，所以F为A1B的中点．又因为E是BC的中点，所以EF∥A1C.因为EF⊂平面AB1E，A1C⊄平面AB1E，所以A1C∥平面AB1E.题型三平面图形的翻折问题例3 (2016·全国Ⅱ)如图，菱形ABCD的对角线AC与BD交于点O，AB＝5，AC＝6，点E，F 分别在AD ，CD 上，AE ＝CF ＝54，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置，OD ′＝10.(1)证明：D ′H ⊥平面ABCD ； (2)求二面角BD ′AC 的正弦值． (1)证明 由已知得AC ⊥BD ，AD ＝CD . 又由AE ＝CF 得AE AD ＝CFCD ，故AC ∥EF .因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4. 由EF ∥AC 得OH DO ＝AE AD ＝14.所以OH ＝1，D ′H ＝DH ＝3.于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH . 又D ′H ⊥EF ，而OH ∩EF ＝H ， 所以D ′H ⊥平面ABCD .(2)解 如图，以H 为坐标原点，HF ，HD ，HD ′所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，则H (0,0,0)，A (－3，－1,0)，B (0，－5,0)，C (3，－1,0)，D ′(0,0,3)，AB →＝(3，－4,0)，AC →＝(6,0,0)，AD ′—→＝(3,1,3)． 设m ＝(x 1，y 1，z 1)是平面ABD ′的法向量，则 ⎩⎪⎨⎪⎧m ·AB →＝0，m ·AD ′→＝0，即⎩⎪⎨⎪⎧3x 1－4y 1＝0，3x 1＋y 1＋3z 1＝0，所以可取m ＝(4,3，－5)．设n ＝(x 2，y 2，z 2)是平面ACD ′的法向量，则⎩⎪⎨⎪⎧n ·AC →＝0，n ·AD ′→＝0，即⎩⎪⎨⎪⎧6x 2＝0，3x 2＋y 2＋3z 2＝0，所以可取n ＝(0，－3,1)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝－1450×10＝－7525，sin 〈m ，n 〉＝29525.因此二面角BD ′AC 的正弦值是29525.跟踪训练3 如图(1)，四边形ABCD 为矩形，PD ⊥平面ABCD ，AB ＝1，BC ＝PC ＝2，作如图(2)折叠，折痕EF ∥DC .其中点E ，F 分别在线段PD ，PC 上，沿EF 折叠后，点P 叠在线段AD 上的点记为M ，并且MF ⊥CF .(1)证明：CF ⊥平面MDF ； (2)求三棱锥M －CDE 的体积．(1)证明 因为PD ⊥平面ABCD ，AD ⊂平面ABCD ， 所以PD ⊥AD .又因为ABCD 是矩形，CD ⊥AD ， PD ∩CD ＝D ，PD ，CD ⊂平面PCD ， 所以AD ⊥平面PCD .又CF ⊂平面PCD ，所以AD ⊥CF ，即MD ⊥CF . 又MF ⊥CF ，MD ∩MF ＝M ，MD ，MF ⊂平面MDF ， 所以CF ⊥平面MDF .(2)解 因为PD ⊥DC ，PC ＝2，CD ＝1，∠PCD ＝60°， 所以PD ＝3，由(1)知FD ⊥CF ， 在Rt △DCF 中，CF ＝12CD ＝12.如图，过点F 作FG ⊥CD 交CD 于点G ， 得FG ＝FC sin 60°＝12×32＝34，所以DE ＝FG ＝34，故ME ＝PE ＝3－34＝334， 所以MD ＝ME 2－DE 2＝⎝⎛⎭⎫3342－⎝⎛⎭⎫342＝62.S △CDE ＝12DE ·DC ＝12×34×1＝38.故V 三棱锥M －CDE ＝13MD ·S △CDE ＝13×62×38＝216.题型四 立体几何中的存在性问题例4 (2017·安徽江南名校联考)如图，在四棱锥P —ABCD 中，PD ⊥平面ABCD ，AB ∥DC ，AB ⊥AD ，DC ＝6，AD ＝8，BC ＝10，∠P AD ＝45°，E 为P A 的中点．(1)求证：DE ∥平面BPC ；(2)线段AB 上是否存在一点F ，满足CF ⊥DB ？若存在，请求出二面角F —PC —D 的余弦值；若不存在，请说明理由．(1)证明 取PB 的中点M ，连接EM 和CM ，过点C 作CN ⊥AB ，垂足为点N . 在平面ABCD 内，∵CN ⊥AB ，DA ⊥AB ，∴CN ∥DA ，又AB ∥CD ，∴四边形CDAN 为平行四边形， ∴CN ＝AD ＝8，DC ＝AN ＝6， 在Rt △BNC 中，BN ＝BC 2－CN 2＝102－82＝6，∴AB ＝12，而E ，M 分别为P A ，PB 的中点， ∴EM ∥AB 且EM ＝6，又DC ∥AB ，∴EM ∥CD 且EM ＝CD ，四边形CDEM 为平行四边形， ∴DE ∥CM .∵CM ⊂平面PBC ，DE ⊄平面PBC ， ∴DE ∥平面BPC .(2)解 由题意可得DA ，DC ，DP 两两互相垂直，如图，以D 为原点，DA ，DC ，DP 所在直线分别为x ，y ，z 轴建立空间直角坐标系Dxyz ，则A (8,0,0)，B (8,12,0)，C (0,6,0)，P (0,0,8)．假设AB 上存在一点F 使CF ⊥BD ，设点F 的坐标为(8，t,0)(0<t <12)， 则CF →＝(8，t －6,0)，DB →＝(8,12,0)， 由CF →·DB →＝0，得t ＝23.又平面DPC 的一个法向量为m ＝(1,0,0)， 设平面FPC 的法向量为n ＝(x ，y ，z )． 又PC →＝(0,6，－8)，FC →＝⎝⎛⎭⎫－8，163，0. 由⎩⎪⎨⎪⎧ n ·PC →＝0，n ·FC →＝0，得⎩⎪⎨⎪⎧6y －8z ＝0，－8x ＋163y ＝0， 即⎩⎨⎧z ＝34y ，x ＝23y ，不妨令y ＝12，则n ＝(8,12,9)．则cos 〈n ，m 〉＝n·m|n||m |＝81×82＋122＋92＝817. 又由图可知，该二面角为锐二面角， 故二面角F —PC —D 的余弦值为817.思维升华 对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论则否定假设．跟踪训练4 (2018·成都模拟)如图，在四棱柱ABCD －A 1B 1C 1D 1中，侧棱A 1A ⊥底面ABCD ，AB ∥DC ，AB ⊥AD ，AD ＝CD ＝1，AA 1＝AB ＝2，E 为棱AA 1的中点．(1)证明：B 1C 1⊥CE ；(2)求二面角B 1－CE －C 1的正弦值；(3)设点M 在线段C 1E 上，且直线AM 与平面ADD 1A 1所成角的正弦值为26，求线段AM 的长． (1)证明 如图，以点A 为原点，分别以AD ，AA 1，AB 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系，由题意得A (0,0,0)，B (0,0,2)，C (1,0,1)，B 1(0,2,2)，C 1(1,2,1)，E (0,1,0)．易得B 1C 1—→＝(1,0，－1)，CE →＝(－1,1，－1)，于是B 1C 1—→·CE →＝0，所以B 1C 1⊥CE .(2)解 B 1C —→＝(1，－2，－1)．设平面B 1CE 的法向量m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ m ·B 1C —→＝0，m ·CE →＝0，即⎩⎪⎨⎪⎧x －2y －z ＝0，－x ＋y －z ＝0. 消去x ，得y ＋2z ＝0，不妨令z ＝1，可得一个法向量为m ＝(－3，－2,1)．由(1)知，B 1C 1⊥CE ，又CC 1⊥B 1C 1，CC 1∩CE ＝C ，CC 1，CE ⊂平面CEC 1，可得B 1C 1⊥平面CEC 1，故B 1C 1—→＝(1,0，－1)为平面CEC 1的一个法向量．于是cos 〈m ，B 1C 1—→〉＝m ·B 1C 1—→|m ||B 1C 1—→|＝－414×2＝－277，从而sin 〈m ，B 1C 1—→〉＝217， 所以二面角B 1－CE －C 1的正弦值为217. (3)解 AE →＝(0,1,0)，EC 1→＝(1,1,1)，设EM →＝λEC 1→＝(λ，λ，λ)(0≤λ≤1)，则AM →＝AE →＋EM →＝(λ，λ＋1，λ)．可取AB →＝(0,0,2)为平面ADD 1A 1的一个法向量．设θ为直线AM 与平面ADD 1A 1所成的角，则sin θ＝|cos 〈AM →，AB →〉|＝|AM →·AB →||AM →||AB →|＝2λλ2＋(λ＋1)2＋λ2×2＝λ3λ2＋2λ＋1， 于是λ3λ2＋2λ＋1＝26，解得λ＝13(负值舍去)， 所以AM ＝ 2.。

.WORD 格式整理 ..高中数学《立体几何》大题及答案解析( 理)1.（ 2009 全国卷Ⅰ）如图，四棱锥S ABCD 中，底面 ABCD 为矩形， SD底面ABCD，AD 2 ，DC SD 2 ，点 M 在侧棱 SC 上，∠ABM=60。

（I ）证明：M是侧棱SC的中点；求二面角 S AM B 的大小。

2.（ 2009 全国卷Ⅱ）如图，直三棱柱ABC-A 1B1C1中， AB ⊥ AC,D 、E 分别为 AA 1、 B1C 的中点，DE ⊥平面 BCC 1（Ⅰ）证明： AB=AC（Ⅱ）设二面角A-BD-C 为 60°,求 B 1C 与平面 BCD 所成的角的大小A 1C1 B1D EAC B3. （ 2009浙江卷）如图， DC平面 ABC， EB//DC ， AC BC EB 2DC 2，ACB120 ， P,Q 分别为 AE , AB 的中点．（I）证明： PQ / / 平面ACD；（II）求AD与平面 ABE 所成角的正弦值．.WORD 格式整理 ..4.（ 2009 北京卷）如图，四棱锥P ABCD 的底面是正方形，PD 底面ABCD ，点E在棱PB上.（Ⅰ）求证：平面AEC平面PD B；（Ⅱ）当 PD2AB 且E为PB的中点时，求 AE 与平面 PDB 所成的角的大小.5.（ 2009 江西卷）如图，在四棱锥P ABCD 中，底面 ABCD 是矩形， PA平面ABCD，PA AD 4 ， AB 2 ．以 BD 的中点 O 为球心、 BD 为直径的球面交PD于点 M ．（1）求证：平面ABM⊥平面PCD；（2）求直线PC与平面ABM所成的角；（3）求点O到平面ABM的距离．PMA DOBC6（. 2009 四川卷）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ ABE是等腰直角三角形，AB AE, FA FE, AEF45 （I）求证： EF平面 BCE ；（ II）设线段 CD 、 AE 的中点分别为 P 、 M ，求证： PM ∥平面BCE （ III）求二面角 F BD A 的大小。

高中数学重点突破专项训练立体几何1. 将两块三角板按图甲方式拼好，其中90B D ∠=∠=︒，30ACD ∠=︒，45ACB ∠=︒，2AC =，现将三角板ACD 沿AC 折起，使D 在平面ABC 上的射影恰好在AB 上，如图乙．(1)求证：AD ⊥平面BDC ； (2)求二面角D AC B --的大小；(3)求异面直线AC 与BD 所成角的大小．2. 如图，在正三棱柱111C B A ABC -中，各棱长都等于a ，D 、E 分不是1AC 、1BB 的中点，〔1〕求证：DE 是异面直线1AC 与1BB 的公垂线段，并求其长度；〔2〕求二面角C AC E --1的大小； 〔3〕求点1C 到平面AEC 的距离．3. 如图，在棱长为a 的正方体1111D C B A ABCD -中，E 、F 分不为棱AB 和BC 的中点，EF 交BD 于H ．〔1〕求二面角B EF --1β的正切值；〔2〕试在棱B B 1上找一点M ，使⊥M D 1平面1EFB ，并证明你的结论；〔3〕求点1D 到平面1EFB 的距离．4. 如图，斜三棱柱ABC —A 1B 1C 1的底面是直角三角形，AC ⊥CB ，∠ABC=45°，侧面A 1ABB 1是边长为a 的菱形，且垂直于底面ABC ，∠A 1AB=60°，E 、F 分不是AB 1、 BC 的中点.〔1〕求证EF//平面A 1ACC 1；〔2〕求EF 与侧面A 1ABB 1所成的角； 〔3〕求三棱锥A —BCE 的体积.5. 直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分不为B 1A 、C 1C 、BC 的中点。

〔I 〕求证：DE ∥平面ABC ； 〔II 〕求证：B 1F ⊥平面AEF ；〔III 〕求二面角B 1—AE —F 的大小〔用反三角函数表示〕。

6. 在直角梯形ABCD 中，∠A=∠D=90°，AB ＜CD ，SD ⊥平面ABCD ，AB=AD=a ，S D=a 2，在线段SA 上取一点E 〔不含端点〕使EC=AC ，截面CDE 与SB 交于点F 。

高考数学压轴题突破训练——立体几何1. 1. 如图，平面如图，平面VAD VAD⊥平面⊥平面ABCD ABCD，△，△，△VAD VAD 是等边三角形，是等边三角形，ABCD ABCD 是矩形，是矩形，AB AB AB∶∶AD AD＝＝2∶1，F 是AB 的中点．的中点．（1）求VC 与平面ABCD 所成的角；所成的角； （2）求二面角V-FC-B 的度数；的度数；（3）当V 到平面ABCD 的距离是3时，求B 到平面VFC 的距离．的距离．2.2.如图正方体如图正方体ABCD-1111D C B A 中，中，E E 、F 、G 分别是B B 1、AB AB、、BC 的中点．的中点．（1）证明：F D 1⊥EG EG；； （2）证明：F D 1⊥平面AEG AEG；； （3）求AE <cos ，>B D 1．3. 3. 在直角梯形在直角梯形P 1DCB 中，中，P P 1D//CB D//CB，，CD//P 1D 且P 1D D = = 6，BC = = 33，DC =6，A 是P 1D 的中点，沿AB 把平面P 1AB 折起到平面PAB 的位置，使二面角P －CD CD－－B 成45°角，设E 、F 分别是线段AB AB、、PD 的中点．的中点． （（1）求证：）求证：AF//AF//AF//平面平面PEC PEC；； （（2）求平面PEC 和平面PAD 所1. 1. 如图，平面如图，平面VAD VAD⊥平面⊥平面ABCD ABCD，△，△，△VAD VAD 是等边三角形，ABCD 是矩形，是矩形，AB AB AB∶∶AD AD＝＝2∶1，F 是AB 的中点．的中点．D B C F E A P （1）求VC 与平面ABCD 所成的角；所成的角； （2）求二面角V-FC-B 的度数；的度数；（3）当V 到平面ABCD 的距离是3时，求B 到平面VFC 的距离．的距离．2.2.如图正方体如图正方体ABCD-1111D C B A 中，中，E E 、F 、G 分别是B B 1、AB AB、、BC 的中点．的中点．（1）证明：F D 1⊥EG EG；； （2）证明：F D 1⊥平面AEG AEG；； （3）求AE <cos ，>B D 1．3. 3. 在直角梯形在直角梯形P 1DCB 中，中，P P 1D//CB D//CB，，CD//P 1D 且P 1D D = = 6，BC = = 33，DC =6，A 是P 1D 的中点，沿AB 把平面P 1AB 折起到平面PAB 的位置，使二面角P －CD CD－－B 成45°角，设E 、F 分别是线段AB AB、、PD 的中点．的中点． （（1）求证：）求证：AF//AF//AF//平面平面PEC PEC；； （（2）求平面PEC 和平面PAD 所成的二面角的大小；所成的二面角的大小； （（3）求点D 到平面PEC 的距离．的距离． 成的二面角的大小；成的二面角的大小； （（3）求点D 到平面PEC 的距离．的距离．BC DA P 1 DBCF E A P4. 4. 如图四棱锥如图四棱锥ABCD P -中，中，^PA 底面ABCD ，4=PA 正方形的边长为2 （1）求点A 到平面PCD 的距离；的距离；（2）求直线PA 与平面PCD 所成角的大小；所成角的大小； （3）求以PCD 与PAC 为半平面的二面角的正切值。