现代控制理论 东北大学高立群 清华大学出版社 第3章

现代控制理论（浓缩版）绪论1．经典控制理论与现代控制理论的比较。

经典控制理论也称为古典控制理论，多半是用来解决单输入-单输出的问题，所涉及的系统大多是线性定常系统，非线性系统中的相平面法也只含两个变量。

经典控制理论是以传递函数为基础、在频率域对单输入单输出控制系统进行分析和设计的理论。

它明显具有依靠手工进行分析和综合的特点，这个特点是与20世纪40~50年代生产发展的状况，以及电子计算机的发展水平尚处于初级阶段密切相关的。

在对精度要求不高的场合是完全可用的。

最大成果之一就是PID 控制规律的产生，PID 控制原理简单，易于实现，具有一定的自适应性与鲁棒性，对于无时间延时的单回路控制系统很有效，在工业过程控制中仍被广泛采用。

现代控制理论主要用来解决多输入多输出系统的问题，系统可以是线性或非线性的、定常或时变的。

确认了控制系统的状态方程描述法的实用性，是与状态方程有关的控制理论。

现代控制理论基于时域内的状态空间分析法，着重实现系统最优控制的研究。

从数学角度而言，是把系统描述为四个具有适当阶次的矩阵，从而将控制系统的一些问题转化为数学问题，尤其是线性代数问题。

而且，现代控制理论是以庞得亚金的极大值原理、别尔曼的动态规划和卡尔曼的滤波理论为其发展里程碑，揭示了一些极为深刻的理论结果。

面对现代控制理论的快速发展及成就，人们对这种理论应用于工业过程寄于乐期望。

但现代控制在工业实践中遇到的理论、经济和技术上的一些困难。

所以说，现代控制理论还存在许多问题，并不是“完整无缺”，这是事物存在矛盾的客观反应，并将推动现代控制理论向更深、更广方向发展。

如大系统理论和智能控制理论的出现，使控制理论发展到一个新阶段。

2．控制一个动态系统的几个基本步骤有四个基本步骤：建模，基于物理规律建立数学模型；系统辨识，基于输入输出实测数据建立数学模型；信号处理，用滤波、预报、状态估计等方法处理输出；综合控制输入，用各种控制规律综合输入。

前言
本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答，可帮助同学学习和理解教材的内容。由于习题数量较多，难易程度不同，虽然主要对象是研究型大学自动化专业本科学生，但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答；第4、7 章由井元伟教授组织编选和解答，第1、2章由郑艳副教授组织编选和解答。
+
若取 ，则有
（2）解 由（1）知
取 ，则有
若取 ，则有 ，
3.11 求下列系统在输入作用为：① 脉冲函数；② 单位阶跃函数；③ 单位斜坡函数下的状态响应。
(1)
(2)
图P2.2
解 这是一个物理系统，采用机理分析法求状态空间表达式会更为方便。令 为输入量，即 ， ， 的位移量 ， 为输出量，
选择状态变量 ， = ， = ， 。
根据牛顿定律对 有：
对 有：
经整理得：
状态方程为：
输出方程为：
写成矩阵形式为：
2.5 系统的结构如图P2.5所示。以图中所标记的 、 、 作为状态变量，推导其状态空间表达式。其中， 、 分别为系统的输入、输出， 、 、 均为标量。
图P2.5系统结构图
解 图P2.5给出了由积分器、放大器及加法器所描述的系统结构图，且图中每个积分器的输出即为状态变量，这种图形称为系统状态变量图。状态变量图即描述了系统状态变量之间的关系，又说明了状态变量的物理意义。由状态变量图可直接求得系统的状态空间表达式。
(2) 解 由已知得：
，
令： ，
得：
状态变量图如下：

特点
现代控制理论强调数学建模、系统分析和优化，注重实际应用和工程实现，具有广泛的应用领域和重要的实际意 义。
现代控制理论的重要性
推动自动化技术发展
促进科技创新
现代控制理论是自动化技术的重要基 础，为工业自动化、智能制造等领域 提供了重要的理论支持和技术手段。
现代控制理论的发展和应用，推动了 科技创新和产业升级，为经济发展和 社会进步做出了重要贡献。
考试
期末闭卷考试，涵盖了课程的所有重点内容，包括系统建模、稳定性分析、状态反馈和 最优控制等。
学习效果评估
要点一
作业成绩
根据学生提交的作业，评估学生对控制理论知识的掌握程 度和应用能力。
要点二
考试成绩
根据期末考试成绩，评估学生对整个课程内容的掌握程度 。
教学改进建议
增加实践环节
为了提高学生的实际操作能力和 问题解决能力，建议增加实验或 实践环节，让学生亲自动手进行
课程目标
1
掌握现代控制理论的基本概念、原理和方法。
2
学会分析和设计控制系统，提高解决实际问题的 能力。
3
培养学生对控制理论的兴趣和热情，为后续学习 和工作打下基础。
02 现代控制理论概述
定义与特点
定义
现代控制理论是一门研究系统状态和行为变化规律的科学，通过数学模型和计算机仿真技术实现系统的分析和优 化。
状态转移矩阵的求解
02
通过系统的状态方程，求解状态转移矩阵，从而得到系统状态
的转移关系。
系统的稳定性分析
03
通过分析状态转移矩阵的性质，判断系统的稳定性，为后续控
制设计提供依据。
线性系统的状态反馈与极点配置
状态反馈控制器的设计
根据系统状态和期望的输出，设计状态反馈控制器，使得系统状态 能够跟踪期望的轨迹统的动态特性，实现系统性能的 优化。

x1能控，x2不能控 状态不完全能控
不能控系统
3.2.1 具有Jordan标准型系统能控性判别
通过以上分析，可以得出以下几点结论： 1）系统的能控性，取决于状态方程中的系统矩阵 A和控制矩阵b。 系统矩阵A是由系统的结构和内部参数决定的； 控制矩阵b是与控制作用的施加点有关的，因此系 统的能控性完全取决于系统的结构、参数，以及控 制作用的施加点。
3.1 能控性的定义
2. 线性连续时变系统的能控性
x A(t)x B(t)u
能控性的定义，与定常系统的定义相同，但是A(t)、 B(t)是时变矩阵不是而常系数矩阵，其状态矢量x(t) 的转移，与初始时刻t0的选取有关，所以在时变系 统能控性定义中，应强调在t0时刻系统是能控的 。
3.1 能控性的定义
(6)
x2
0
4
0
x2
4
u
x3 0 0 2 x3 0
状态不完全能控，不能控系统
3.2.1 具有Jordan标准型系统能控性判别
(7)
x1 x2
1
0
1
1
0
x1
0
0 x2 b2 u
x3
0
0
2
x3
b3
状态完全能控，能控系统
3.2.1 具有Jordan标准型系统能控性判别
1.单输入系统 x Ax bu
为简明起见，列举具有Jordan标准型的二阶系统， 对能控性加以分析。 例 (1)
x
1
0
0 0
2
x
b2
u
;
y c1 c2 x
3.2 线性定常系统的能控性判别
即 系统模拟结构图：
x1不能控，x2能控 状态不完全能控

1.1 控制理论的发展历程
1.1.1 经典控制理论
• 1788年，英国瓦特（J.Watt） 利用负反馈原理设计的用来控制 蒸汽机转速的离心调速器，亦称 飞球调速器/控制器-----第一个自 动控制系统，首次应用于工业， 拉开了控制理论发展的序幕。 • 1868年，英国麦克斯韦（J.C.Maxwell）发表了 《论调速器》，指出微分方程特征根的位置（在左 半面或右半面）跟稳定有关，开辟用数学方法研究 控制系统中运动现象的途径。
•
1954年，钱学森的《工程控制论》在美国出版。 －－－奠定了工程控制论的基础
我国自动控制界的先驱式人物、中国导 弹之父、《工程控制论》作者--钱学森
“钱学森无论走到哪里，都抵得上5个师的兵力，我宁可把他击毙在美 国也不能让他离开。”----美国海军高级将领金布尔
• 1934年上海交通大学毕业，次年留学美国 • 1938年在美国从事空气动力学研究 • 1939年加州理工学院获得航空、数学博士学位，曾任加 州理工学院副教授，麻省理工学院教授，加州理工学院 喷气推进中心主任、教授。 • 40年代末加州理工学院给研究生讲课 • 1955年一家乘克莱弗兰总统号回国 • 1964年我国第一颗原子弹爆炸成功 • 1967年我国第一颗氢弹爆炸成功 • 1970年我国第一颗人造卫星东方红一号上天 • 1989年获“小罗克韦尔奖章”（1982创立-1/16） • 2009年10月31日在北京逝世
现代控制理论 Modern Control Theory 绪 论
• 教材： 刘豹、唐万生主编，现代控制理论(第三版)，机械工业出版社， 2006 • 参考资料： 张嗣瀛、高立群，《现代控制理论》，清华大学出版社,2006 俞立主编，《现代控制理论》，清华大学出版社，2007 袁德成等主编《现代控制理论》，清华大学出版社，2007 曲延滨、王新生主编，《现代控制理论基础》，哈尔滨工业大 学出版社，2005 …… • 课时：32 考查方式：考试70% + 考勤10% + 作业20%

第一和第二讲小结一、状态空间表达式的标准形式能控标准形能观测标准形对角线标准形Jordan标准形二、矩阵的特征值及对角线化矩阵是能控标准形时的变换矩阵求法（1）特征值互异（2）重根（3）一般情形三、利用MATLAB进行系统模型之间的相互转换[A, B, C, D] = tf2ss (num, den)[num,den] = ss2tf [A,B,C,D,iu]四、时域分析的基本概念状态转移矩阵及其性质，凯莱-哈密尔顿定理最小多项式五、矩阵指数计算级数法，对角线标准形与Jordan标准形法拉氏变换法凯莱-哈密尔顿定理II、分析部分第三章线性多变量系统的能控性与能观测性分析能控性(controllability)和能观测性(observability)深刻地揭示了系统的内部结构关系，由R.E.Kalman于60年代初首先提出并研究的这两个重要概念，在现代控制理论的研究与实践中，具有极其重要的意义，事实上，能控性与能观测性通常决定了最优控制问题解的存在性。

例如，在极点配置问题中，状态反馈的的存在性将由系统的能控性决定；在观测器设计和最优估计中，将涉及到系统的能观测性条件。

在本章中，我们的讨论将限于线性系统。

将首先给出能控性与能观测性的定义，然后推导出判别系统能控和能观测性的若干判据。

3.1 线性连续系统的能控性3.1.1 概述能控性和能观测性就是研究系统这个“黑箱”的内部的状态是否可由输入影响和是否可由输出反映。

例1． 给定系统的描述为u x x xx⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡2150042121 []⎥⎦⎤⎢⎣⎡-=2160x x y将其表为标量方程组的形式，有：u x x+=114 u x x2522+-= 26x y -=例3－2：判断下列电路的能控和能观测性)(t u +yCR )(t uR L y23.1.2 能控性的定义考虑线性时变系统的状态方程∑:Bu x t A x+=)( ， u t D x t C t y )()()(+=，00)(x t x =，J t ∈ (3.1.1)其中，x 为n 维状态向量，u 维p 维输入向量，J 为时间定义区间，B A ,分别为n n ⨯和p n ⨯的元为t 的连续函数的矩阵。

3.2.2 状态能观性的判据 已知系统的动态方程
x’(t ) A(t ) x(t )
y C (t ) x(t )
x(0) x0
1、线性定常连续系统能观测性的格拉姆矩阵判据
线性定常连续系统{A，C} 状态完全能观测的充要条件是：存在 时刻t1>t0，使如下定义的能观性格拉姆（Gram)矩阵为非奇异。
16
例：给定线性定常系统的状态方程，判断能控性。
1 x1 1 x1 0 x1 x 2.5 1.5 x 1 u y 1 0 x 2 2 2
解：
1 1 1 0 AB 1 1 2.5 1.5 1 1 rank[ B AB] rank =1 2 系统不能控 1 1 s 1.5 1 1 1 0 s 1 Cadj ( sI A) B s 2.5 1 2.5 g ( s) s 1 sI A ( s 2.5)( s 1) ( s 1) 2.5 s 1.5

0 t1 0
t1
T x0 Wc (t0 , t1 ) x0 [ BT T (t0 , ) x0 ]T BT T (t0 , ) x0 d 0
T x0 Wc
(t0 , t1 ) x0 B (t0 , ) x0 d (t0 , ) x0 0
At k 0 n 1
y (t ) k (t )CAk x(0)
k 0
n 1
y (t ) 0 (t )Cx(0) 1 (t )CAx(0) n 1 (t )CAn 1 x(0) C CA x(0) y (t ) 0 (t ) 1 (t ) ... n 1 (t ) n 1 CA C CA =n rank n 1 CA

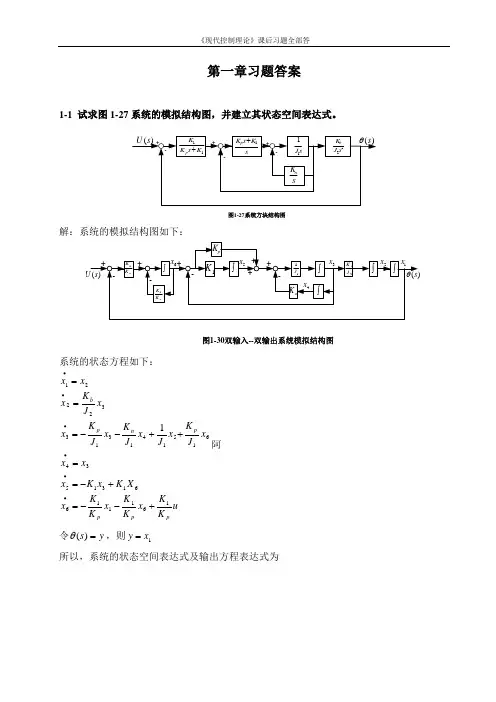
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。

0 1 0 0 1 0 Rc 1 0 0 0 0 0
，
求
得
1 0 0 1 0 0
0 0 1 0 0 0
0 0 0 1 0 0

0
1
0
0
0 0
Rc1


0 0
0 0
0 0 0 1 0 1 1 0
0 1 1 0 0 0
1 0 0 0 0 0


0
0

1
1
1

1
0
,
0

0
0

Co 0m
0m
Im


0 0
0 0
0 0
0 0
1 0 0 1
第二步: 判别该能观标准型实现的状态
是否完全能控。
M Bo Ao Bo Ao2Bo
0 0 0 0 0 0
0 1 0 0 0 0

1 0
0 0
0 1
本章问题：
1． M b Ab An1b ，n的确定（维 数应为 A 阶数）。 2．矩阵、向量写法的区分。
3．3-3（3） 2、 3讨论较复杂。
W (s)
s2 s2

6s 4s

8 3

1
s2
2s 5 4s
3
所以其能控标准 I 型为
A

0 3
1 4
b

0 1
c

5T 2
d
1
所以其能观标准 II 型为
A

0 3
1 T 4
b

5 2
c

非线性动态系统的稳定性和鲁棒控制理论研究上世纪50年代，Kallman成功的将状态空间法引入到系统控制理论中，从而标志着现代控制理论研究的开始。

现代控制理论的研究对象是系统的数学模型，它根据人们对系统的性能要求，通过对被控对象进行模型分析来设计系统的控制律，从而保证闭环系统具有期望的性能。

其中，线性系统理论已经形成一套完整的理论体系。

过去人们常用线性系统理论来处理很多工程问题，并在一定范围内取得了比较满意的效果。

然而，这种处理方法是以忽略系统中的动态非线性因素为代价的。

实际中很多物理系统都具有固有的动态非线性特性，如库仑摩擦、饱和、死区、滞环等，这些非线性动态非线性特性的存在常常使系统的控制性能下降，甚至变得不稳定。

这就使得利用线性系统理论处理非线性动态系统面临巨大的困难。

此外，在控制系统运行过程中，环境的变化或者元件的老化，以及外界干扰等不确定因素也会造成系统实际参数和标称值之间出现较大差别。

因此，基于标称数学模型所设计的控制律一般很难达到期望的性能指标，甚至会使系统不稳定。

综上所述，研究不确定条件下非线性动态系统的鲁棒稳定性及鲁棒控制间题具有重要的理论意义和迫切的实际需要。

非线性动态系统是指按确定性规律随时间演化的系统，又称动力学系统，其理论来源于经典力学，一般由微分方程来描述。

美国数学家Birkhoff[1]发展了法国数学家Poincare在天体力学和微分方程定性理论方面的研究，奠定了动态系统理论的基础。

在实际动态系统中，对象往往受到各种各样的不确定的影响，所以其数学模型一般不可能精确得到。

因此，我们只能用近似的标称数学模型来描述被控对象，并据此来设计控制系统,动态系统鲁棒控制由此产生。

所谓鲁棒性就是指系统预期非线性动态系统的稳定性和鲁棒控制理论研究的设计品质不因不确定性的存在而遭到破坏的特性，鲁棒控制是非线性动态系统控制理论研究的一个非常重要的分支。

现代控制理论的发展促进了对动态系统的研究，使它的应用从经典力学扩大到一般意义下的系统。

T
（6）
由以上可以看出式（6）中各参数维数如下：
x(t0 )为n 1维向量 B为n r维, AB为n r维, M为n nr维向量 U j为r 1维, U为nr 1维向量
式（6）是关于U的非齐次方程组。由线性代数知识知道，
其有解的充要条件是系数矩阵和增广矩阵的秩相等，即：
rank(M) rankM x(t0 )
+ x1 + C1 R + R 图3-1 电路系统
x2
R -
u
C2 R
由电路理论知识可知, 若图3-1所示的电桥系统是平衡的(例 Z1=Z2=Z3=Z4),电容C2的电压x2(t)是不 能通过输入电压u(t)改变的,即状态变 量x2(t)是不能控的,则系统是不完全能 控的。
+ x1 + C1 R + R R -
为真,则称线性定常连续系统(A,B)状态完全能控。
2. 在上述定义中,对输入u(t)没有加任何约束,只要能使状 态方程的解存在即可。 如果矩阵A(t)和B(t)以及向量u(t)的每个元素都是t 的分段连续函数,则状态方程存在唯一解。 u(t)为分段连续的条件,在工程上是很容易满足的。 3. 在状态能控性定义中,对状态转移的轨迹未加以限制,这 表明能控性是表征系统状态运动的一个定性特性。
或者更确切地说,是状态能控的。
否则,就称系统为不完全能控的。
下面通过实例来说明能控性的意义 。
例1 某电路系统的模型如图3-1所示 。
该电路系统中,电源电压u(t)为 输入变量,并选择两电容器两端 的电压为状态变量x1(t)和x2(t)。 试分析电源电压u(t)对两个状 态变量的控制能力。
因此,给定输入,则一定会存在唯一的输出与之对应。

现代控制理论B（Modern Control Theory）课程代码：05410129学分：2学时：32 (其中：课题教学学时：32 实验学时：0 上机学时：0 课程实践学时:0 )先修课程：自动控制理论、高等数学、线性代数适用专业：自动化教材：现代控制理论（于长官主编、哈尔滨工业大学出版社、第3版,2008，11）一、课程性质与课程目标（一）课程性质（需说明课程对人才培养方面的贡献）《现代控制理论》是自动化专业的一门专业基础课。

它系统介绍基于状态空间描述的控制系统的分析与综合方法。

通过本课程的学习，使学生初步掌握现代控制理论的基本知识及其分析方法，对控制理论有更全面的了解，为后续专业课和毕业设计打好理论基础。

（二）课程目标《现代控制理论》课程主要以控制工程中常见的典型线性连续与离散控制系统为对象，研究建立系统状态空间模型的方法、系统的能控性与能观性判别、系统稳定性分析、系统综合的方法。

课程的具体目标如下：知识目标1.1：了解现代控制理论的体系结构；知识目标1.2：熟练掌握线性控制系统的状态空间描述；知识目标1.3：掌握线性控制时域运动分析与离散化；知识目标1.4：掌握利用状态空间模型分析系统能控性、能观性和稳定性；知识目标1.5：掌握线性定常系统的综合。

能力目标2.1：能够熟练进行系统极点配置的控制器设计，并画出系统结构图。

能力目标2.2：能够熟练进行系统状态观测器的算法设计，并画出系统结构图。

能力目标2.3：逐步培养学生的逻辑思维能力、判断和分析能力。

毕业要求指标点6-3.：能正确认识和评价自动化工程解决方案及新产品、新技术、新工艺、新材料的开发和应用对于客观世界和社会的影响，并理解应承担的责任。

毕业要求指标点7-2：能正确评价复杂自动化工程问题实践对于环境、社会可持续发展的影响。

毕业要求指标点10-3：能够比较熟练地阅读自动化专业的外文书刊资料，能够在跨文化背景下进行沟通、交流和合作。

课程目标毕业要求指标点课程目标1.1课程目标1.2课程目标1.3课程目标1.4课程目标1.5课程目标2.1课程目标2.2课程目标2.36-3 √√√√√√√√7-2 √√√√10-3 √√√√√√√二、课程内容与教学要求第一章绪论（一）课程内容1.本课程的性质、研究对象与方法、目的、任务。

第一章 绪论
1.1.2 现代控制理论(Modern Control) (1950- )

二次世界大战中火炮，雷达，飞机以及通讯系统的控制研 究直接推动了经典控制的发展。五十年代后兴起的现代控 制起源于冷战时期的军备竞赛，如导弹(发射，操纵，指 导及跟踪)，卫星，航天器和星球大战，以及计算机技术 的出现(英国科学家A.J.现代控制 --线性控制系统（Linear
control system ）
中南大学信息科学与工程学院
2014-11-16
1
线性控制系统
第一章 绪论
学时安排

学


时：32
讲授：28 实验：4

学
分： 2
2014-11-16
2
线性控制系统
第一章 绪论
教材


张嗣瀛, 高立群. 现代控制理论，清华 大学出版社，2006 黄家英.自动控制原理（上下册），高等 教育出版社，2010
法分析系统，提出了能控性、能观性、卡尔曼滤波
2014-11-16 等概念，奠定了现代控制理论的基础； 11
线性控制系统
第一章 绪论
1957年成立了国际自动控制联合会（IFAC： International Federation of Automatic Control）。
上世纪60年代末至70年代迅速发展：非线性系统、 大系统和智能系统。
2014-11-16
17
线性控制系统
第一章 绪论

本课程内容
•状态空间模型(modeling)

•基于状态空间模型的系统分析（Analysis）

运动分析、能控性、能观性、稳定性

《现代控制理论》教案大纲第一章：绪论1.1 课程背景与意义1.2 控制系统的基本概念1.3 控制理论的发展历程1.4 教学内容与目标第二章：线性控制系统的基本理论2.1 数学基础2.1.1 向量与矩阵2.1.2 复数与复矩阵2.1.3 拉普拉斯变换与Z变换2.2 线性微分方程2.3 线性差分方程2.4 线性系统的状态空间描述2.5 线性系统的传递函数2.6 小结第三章：线性控制系统的稳定性分析3.1 系统稳定性的概念3.2 劳斯-赫尔维茨稳定性判据3.3 奈奎斯特稳定性判据3.4 李雅普诺夫稳定性理论3.5 小结第四章：线性控制系统的性能分析与设计4.1 性能指标4.1.1 稳态性能4.1.2 动态性能4.2 控制器设计方法4.2.1 比例积分微分（PID）控制器4.2.2 状态反馈控制器4.2.3 观测器设计4.3 小结第五章：非线性控制系统理论5.1 非线性系统的基本概念5.2 非线性方程与非线性微分方程5.3 非线性系统的状态空间描述5.4 非线性系统的稳定性分析5.5 小结第六章：非线性控制系统的性能分析与设计6.1 非线性性能指标6.2 非线性控制器设计方法6.2.1 反馈线性化方法6.2.2 滑模控制方法6.2.3 神经网络控制方法6.3 小结第七章：鲁棒控制理论7.1 鲁棒控制的概念与意义7.2 鲁棒控制的设计方法7.2.1 定义1-范数方法7.2.2 H∞控制方法7.2.3 μ-综合方法7.3 小结第八章：自适应控制理论8.1 自适应控制的概念与意义8.2 自适应控制的设计方法8.2.1 模型参考自适应控制8.2.2 适应律与自适应律8.2.3 自适应控制器的设计步骤8.3 小结第九章：现代控制理论在工程应用中的案例分析9.1 工业过程控制中的应用9.2 控制中的应用9.3 航空航天领域的应用9.4 小结第十章：总结与展望10.1 现代控制理论的主要成果与贡献10.2 现代控制理论的发展趋势10.3 面向未来的控制挑战与机遇10.4 小结重点和难点解析重点环节一：第二章中向量与矩阵、复数与复矩阵、拉普拉斯变换与Z变换的数学基础。

第3章 “状态方程的解”习题解答3.1计算下列矩阵的矩阵指数te A 。

200200(1)020;(2)031002003--⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦A A0001(3) ; (4) 1040-⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A A（1）解 222000000tt t t e e e e ---⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A （2）解 233300000tt t t t e e e te e ----⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A （3）解()122011001111s s s s s s s s s s -⎡⎤-=⎢⎥-⎣⎦⎡⎤⎢⎥⎡⎤-==⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦I A I A ()()()11101t t e L s t t --⎡⎤⎡⎤=-=⎢⎥⎣⎦⎣⎦A I A （4）解： 14s s s ⎡⎤-=⎢⎥-⎣⎦I A()1222221144124242244s s s s ss s s s s --⎡⎤-=⎢⎥+⎣⎦⎡⎤-⋅⎢⎥++=⎢⎥⎢⎥⎢⎥++⎣⎦I A 221221242422441cos 2sin 222sin 2cos 2ts s s e L s s s t t tt -⎡⎤-⎢⎥++=⎢⎥⎢⎥⎢⎥++⎣⎦⎡⎤-⎢⎥=⎢⎥⎣⎦A3.2 已知系统状态方程和初始条件为()1001010,000121⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x x x(1) 试用拉氏变换法求其状态转移矩阵； (2) 试用化对角标准形法求其状态转移矩阵； (3) 试用化te A 为有限项法求其状态转移矩阵； (4) 根据所给初始条件，求齐次状态方程的解。

（1）解 12100010012O O ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦A A A ， 其中， 12101,12⎡⎤==⎢⎥⎣⎦A A则有 1200ttt e ee ⎡⎤=⎢⎥⎣⎦A A A 而 1tt ee =A ， ()2112t e L s --⎡⎤=-⎣⎦A I A()112101220111(1)(2)101111212s s s s s s s s s s s ---⎡⎤-=⎢⎥--⎣⎦-⎡⎤=⎢⎥---⎣⎦⎡⎤⎢⎥-=⎢⎥⎢⎥-⎢⎥---⎣⎦I A()2112220ttt tt e eL s e e e --⎡⎤⎡⎤=-=⎢⎥⎣⎦-⎣⎦A I A 所以状态转移矩阵为()112200000tt t t tt e e L s e e e e --⎡⎤⎢⎥⎡⎤=-=⎢⎥⎣⎦⎢⎥-⎣⎦A I A （2）解 21(1)(2)012I λλλλλ--==--=--A121,2λλ==对于11λ=，100011101⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦1P P 对于22λ=，2210001001⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦P P110101111-⎡⎤⎡⎤=⇒=⎢⎥⎢⎥-⎣⎦⎣⎦P P2122220010100111100t tt t t tt t t e ee e e e e ee -⎡⎤=⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥-⎣⎦A P P2200000t t t t tt e e e e e e ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦P （3）解 矩阵的特征值为1,21λ=, 32λ=对于32λ=有： 2012()2()4()te t t t ααα=++对于1,21λ=有： 012()()()te t t t ααα=++因为是二重特征值，故需补充方程 12()2()tte t t αα=+ 从而联立求解，得：202122()2()322()t tt t t t t tt e te t te e e t e e te ααα=-=-+=--()()20122222222()()()20100020322010002012100100 0100100120120000 0t t t t t t t t t t t t t tt t tt e t t t e te e te te e e e te e e te e e e e e ααα=++⎡⎤-⎡⎤⎢⎥⎢⎥=-+-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥+--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦A I A A（4）解：0)0222()()(0)001000001t t t t t t t tt t t e t e e e e e e e e -==⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A(A x x x3.3 矩阵A 是22⨯的常数矩阵，关于系统的状态方程式= xAx ，有 1(0)1⎡⎤=⎢⎥-⎣⎦x 时， 22t t e e --⎡⎤=⎢⎥-⎣⎦x2(0)1⎡⎤=⎢⎥-⎣⎦x 时， 2t t e e --⎡⎤=⎢⎥-⎣⎦x试确定这个系统的状态转移矩阵(,0)t Φ和矩阵A 。

则必能通过非奇异变换 xTx 实现系统的标准分解，其表达
式为
xC ,O
xC ,NO
x NC x NC ,
,O NO
A11 A21
0
0
0 A22 0 0
A13 A23 A33 A43
0
A24
xC ,O xC ,NO
B1
B
2
u
0 A44
x NC ,O x NC ,NO
解: 因为
0 14
rankrM ab nA k bA2bra 0 nk0 0 2n
1 3 9
0 1 0
所以系统不完全能控。构造变换阵来自T00
1
1 3 0
其逆阵为
3 0 1
T
1
1
0
0
0 1 0
21
则
3 0 11 2 10 1 0 0 3 2
A T 1AT 1 0 00 1
《孔雀东南飞》写作的时代背景
• 取材于东汉献帝年间发生在庐江郡（治舒县 ，汉末迁皖县，均在今安徽境内）的一桩婚姻悲 剧。故事发生在“汉末建安中”。汉武帝时，“ 罢黜百家，独尊儒术”。儒家的那套伦理纲常， 逐渐占据了统治地位，并发展到了相当完备严密 的程度。在婚姻制度方面就规定有“七出”、“ 天下无不是之父母”等清规戒律。“天下无不是 之父母”，这正是焦刘悲剧的根本原因。在这一 时代氛围里，在焦母的淫威下，焦仲卿敢于站在 兰芝一边，表明与兰芝“结发同枕席，黄泉共为 友”的坚决态度实在是难能可贵的
学法指导
• （一）、全诗很长，可以关注关键的或者精彩的段落，如焦仲卿慕青 回绝焦仲卿，刘兰芝辞别婆婆及小姑子，焦仲卿和刘兰芝分手时，立 誓，兰芝和焦仲卿诀别等。可以从人物动作及对话入手，体会其中的 感情，揣摩人物的心理，分析人物的个性，揣测接下来情节的发展。

GDOU-B-11-213《现代控制理论》教学大纲课程简介教学内容本课程主要内容有：系统状态空间表达式的建立；状态方程的求解；系统的能控性和能观性，包括系统能控性和能观性的判别，能控标准型与能观标准型，线性系统的结构分解，传递函数矩阵的实现；李亚普诺夫方法原理及用李亚普诺夫方法分析线性定常、线性时变及非线性系统；控制系统的综合，包括反馈的各种类型，用状态反馈进行极点配置，用状态观测器实现状态反馈等。

修读专业：自动化专业先修课程：线性代数、矩阵论、经典控制理论教材：王孝武，《现代控制理论基础》，机械工业出版社，1998。

一、课程的性质与任务本课程是在经典控制论基础上学习现代控制理论的基本概念、基本理论和分析方法。

现代控制理论基础以状态空间分析法为核心，涵盖了非线性控制系统分析、动态系统最优控制方法。

通过本课程的学习，使学生能够初步掌握现代控制理论的基本知识及其分析方法，并将其应用于实际控制系统的分析与综合，提高学生的系统分析和综合能力。

二、课程的基本要求通过本课程的学习,学生应该掌握有关运用状态空间分析法定量和定性分析及综合控制系统的基本理论、基本方法,为学习后续课程打下基础。

三、修读专业电气工程及其自动化、自动化四、本课程与其它课程的联系本课程为自动化专业的专业课，是继经典控制理论---《自动控制原理》之后的又一门重要的控制理论课程。

其任务是在经典控制理论的基础上进一步加深、扩展和提高学生在控制理论方面的基础知识，使学生较为全面地了解和掌握控制理论的基本内容，为后继学习《最优控制》、《随机控制》、《系统辨识》等其它自控理论课程打好基础。

要求学生具备微分方程、线性代数、积分变换(特别是拉氏变换，z变换)等数学方面的有关知识。

五、教学内容安排、要求、学时分配及作业第一章控制系统的数学模型（10学时）1.状态空间表达式（A）2.由微分方程求状态空间表达式（B）3.传递函数矩阵（A）4.线性变换（B）5.组合系统的数学描述（C）6.作业一次第二章线性控制系统的运动分析(10学时)1.线性定常系统齐次状态方程的解（A）2.状态转移矩阵（A）3.线性定常系统非齐次状态方程的解（B）4.线性系统的脉冲响应矩阵（B）5.作业一次第三章控制系统的能控性和能观测性(14学时)1.能控性及其判据（A）2.能观测性及其判据（A）3.对偶原理（B）4.能控标准形和能观测标准形（A）5.能控性、能观测性与传递函数关系（B）6.系统的结构分解（A）7.实现问题（B）8.作业一次第四章控制系统的稳定性(8学时)1.稳定性的定义(B)李雅普诺夫稳定性定义、稳定、渐进稳定和不稳定的概念；（B）BIBO稳定性的概念（C）2．李雅普诺夫稳定性的基本定理（B）李雅普诺夫稳定性的基本定理（B）李雅普诺夫第二方法在线性定常系统中的应用（C）作业一次第五章线性定常系统的综合(12学时)1.状态反馈和输出反馈（B）2.反馈系统的能控性和能观测性（B）3.极点配置问题（A）4.镇定问题（A）5.状态重构和状态观测器（A）6.带有观测器的状态反馈系统（B）7.解耦问题（B）8.作业一次六、实验内容与要求七、教材与参考书本课程选用教材：王孝武，《现代控制理论基础》，机械工业出版社，1998本课程推荐参考书：1.胡寿松，《自动控制原理》，科学出版社。