【高中数学精品课件】正弦函数的图象及性质

y
1 -4 -3 -2 -
o
-1

2
3
4
5
6
x
y=sinx (xR) 职业中学 2018.3
2018年3月21日星期三
1
一.正弦函数y=sinx的图像
y 1
五点法：
2
(0,0)
-1
o
( ,1) ( 2 , 0 ) ( , 0 ) 2 x 3 3 2 2 ,1) 2( 2
y
-
sin(x+2k)=sinx, kZ 1.y=sinx x[0,2] y=sinx xR 1
-4 -3 -2
y-1
1
o


2
3
4ቤተ መጻሕፍቲ ባይዱ
5
6
x
-4
-3
-2
-
o
-1
2
3
4
5
6
x
2
2.y=sinx (xR)
2018年3月21日星期三
二.正弦函数 y=sin x(x∈R) 的性质
2018年3月21日星期三
f（x 2k） f（x），（k Z）
是正弦函数y sin x的周期？为什么？
2
8
性质二：正弦函数 y=sinx周期性
对于一个周期函数f（x），如果在它的所有周 期中存在一个最小的正数，那么这个最小的 正数就叫做它的最小正周期。
y=sinx的最小正周期T=2π
y
1
4 3 2

3 2

2
-1
2
3
4

7 2

5 2
2
3 2
5 2

(1)令 2x－π4＝－π2＋2kπ，k∈Z. 得 x＝－π8＋kπ(k∈Z)，ymax＝3. (2)∵x∈－π6，π2，∴2x＋π3∈0，43π.
令 u＝2x＋π3，则 u∈0，43π.
又∵y＝sin u 在0，π2上单调递增，在π2，43π上单调递减，
∴当 ∴－
u3∈≤02，sin43πu≤时2，，－即当23≤x∈sin－u≤π6，1，π2时，－
训练1
若 函 数 y ＝ sin(ωx ＋ φ)(x∈R ， ω>0 ，
0≤φ<2π) 的 部 分 图 象 如 图 ， 则 ω ＝
π
π
___4_____，φ＝___4_____.
由又图∵象T＝可2ω知π，T4＝∴2ω，＝∴π4.T＝8. ∵在 x＝1 处取得最大值，∴π4＋φ＝π2＋2kπ(k∈Z)， ∴φ＝2kπ＋π4(k∈Z)，∵0≤φ<2π，∴φ＝π4.
第七章 7.3 三角函数的性质与图象 7.3.2 正弦型函数的性质与图象
课标要求
1.能根据y＝Asin(ωx＋φ)的部分图象确定其解析式. 2.会求函数y＝Asin(ωx＋φ)的周期、单调性、最值、对称性. 3.能利用y＝Asin(ωx＋φ析 课时精练
y＝2sinπ4－x＝－2sinx－π4， 令 z＝x－π4，则 y＝－2sin z. ∵z 是 x 的一次函数且单调递增，
题型二 正弦型函数y＝Asin(ωx＋φ)的性质
角度1 正弦型函数的值域、最值
例2
(1)函数 y＝－2sin2x－π4＋1 的最大值是___3____，此时 x＝_－__π8_＋__k_π_(k_∈__Z__). (2)函数 y＝2sin2x＋π3，x∈－π6，π2的值域为__[_－___3_，__2_]____.

立德树人 和谐发展
你能根据诱导公式，以正弦函数的图象为基础，通
过适当的图形变换得到余弦函数的图象吗？
由未知向已知转
y
化

由诱导公式y=
,将正弦函数的图象向左平移 2 个单位即可得到余弦函数的图象.
1
-4
-3
-2
-
o

2
3
4
5
6
x
6
x
-1
正弦曲
线
正弦函数的图象

形状完全一样
y=cosx与 y=sin(x+ ), xR图象相同 只是位置不同
正弦曲线
6
x
学习新知
立德树人 和谐发展
函数y=sinx，x∈R的图象叫做正弦曲线，正弦曲线的散布
有什么特点？ 是一条“波浪起伏”的连续光滑曲线
-6π -5π-4π-3π -2π
1 y
π
-π O
-1
2π
3π
4π
5π
你能画出函数y=|sinx|，x∈[0，2π]的图象吗？
y
1
O
-1
π
2π
x
6πx
合作探究
立德树人 和谐发展
(2)y= －cosx，x [0, 2 ]
(2)按五个关键点列表
3
2
x
0

2
cosx
1
0
-1
0
1
-cosx
-1
0
1
0
-1

2
y=-cosx x [0,2 ]
y
1
●
o
-1 ●
●

2

●

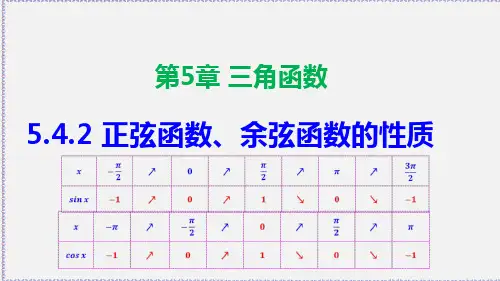
第二步:从圆O1与x轴的交点A起把圆弧分成12等份;
第三步:过圆O1上各分点分别作x轴的垂线,得到对应于角0,
6
,
3
, ,…,2π
2
等分点的正弦值;
第四步:相应地,再把x轴上从0到2π这一段分成12等份;
第五步:再把角x所对应的正弦线向右平移,使它的起点与x轴上表示数x的点重
合;
第六步:最后用光滑曲线把这些正弦线的终点连接起来,就得到了正弦函数
2
2
(4)值域:[-1,1]. 当且仅当x=2kπ+ (k∈Z)时,正弦函数y=sin x取得最大值1;
2
当且仅当x=2kπ- (k∈Z)时,正弦函数y=sin x取得最小值-1.
2
(5)奇偶性:正弦函数y=sin x在R上是奇函数.
(6)对称性:对称轴x=kπ+ ,k∈Z,对称中心(kπ,0),k∈Z.
2
【思考】 (1)-2π是正弦函数的周期吗? 提示:是.2kπ(k∈Z,k≠0)都是它的周期. (2)正弦函数的对称轴之间的距离有什么特点?对称中心呢? 提示:对称轴之间的距离差了π的整数倍.对称中心之间也相差了π的整数倍.
【根底小测】 1.辨析记忆(对的打“√〞,错的打“×〞) (1)正弦函数在区间 [ , 2 ] 上是递增的.( )
2.函数y=sin x是( )
A.增函数
B.减函数
C.偶函数
D.周期函数
【解析】选D.由正弦曲线y=sin x的图象,可得函数y=sin x的增区间是
[2k， (k∈2kZ]),减区间是
2
2
周期为2π的周期函数.
[(k∈2kZ， )3,函数2k是]奇函数,且是
2
2
3.(教材二次开发:例题改编)以下关系式中正确的选项是( ) A.sin 11°<cos 10°<sin 168° B.sin 168°<sin 11°<cos 10° C.sin 11°<sin 168°<cos 10° D.sin 168°<cos 10°<sin 11°

2、本节内容的分析
这节课主要学习正弦函数图像的奇偶性和 单调性，以及性质的应用。这两条性质尤其是 单调性在今后的学习中经常用到，而且在今后 的考试中也是常考的考点之一，因此，我们必 须重视本节课的教学。
3、重点、难点分析
重点：正弦函数图像的的性质及应用 难点：奇偶性、单调性的熟练应用 关键：抓住y=sinx的图象的特征
y
1 -3
5 2
-2

3 2
-
2
o
-1
2

3 2
2
5 2
x
3
7 2
4
y=sinx
返回
85.每一年，我都更加相信生命的浪费是在于：我们没有献出爱，我们没有使用力量，我们表现出自私的谨慎，不去冒险，避开痛苦，也失去了快乐。――[约翰· B· 塔布] 86.微笑，昂首阔步，作深呼吸，嘴里哼着歌儿。倘使你不会唱歌，吹吹口哨或用鼻子哼一哼也可。如此一来，你想让自己烦恼都不可能。――[戴尔· 卡内基] 87.当一切毫无希望时，我看着切石工人在他的石头上，敲击了上百次，而不见任何裂痕出现。但在第一百零一次时，石头被劈成两半。我体会到，并非那一击，而是前面的敲打使它裂开。――[贾柯· 瑞斯] 88.每个意念都是一场祈祷。――[詹姆士· 雷德非] 89.虚荣心很难说是一种恶行，然而一切恶行都围绕虚荣心而生，都不过是满足虚荣心的手段。――[柏格森] 90.习惯正一天天地把我们的生命变成某种定型的化石，我们的心灵正在失去自由，成为平静而没有激情的时间之流的奴隶。――[托尔斯泰] 91.要及时把握梦想，因为梦想一死，生命就如一只羽翼受创的小鸟，无法飞翔。――[兰斯顿· 休斯] 92.生活的艺术较像角力的艺术，而较不像跳舞的艺术；最重要的是：站稳脚步，为无法预见的攻击做准备。――[玛科斯· 奥雷利阿斯] 93.在安详静谧的大自然里，确实还有些使人烦恼.怀疑.感到压迫的事。请你看看蔚蓝的天空和闪烁的星星吧!你的心将会平静下来。[约翰· 纳森· 爱德瓦兹] 94.对一个适度工作的人而言，快乐来自于工作，有如花朵结果前拥有彩色的花瓣。――[约翰· 拉斯金] 95.没有比时间更容易浪费的,同时没有比时间更珍贵的了，因为没有时间我们几乎无法做任何事。――[威廉· 班] 96.人生真正的欢欣，就是在于你自认正在为一个伟大目标运用自己；而不是源于独自发光.自私渺小的忧烦躯壳，只知抱怨世界无法带给你快乐。――[萧伯纳] 97.有三个人是我的朋友爱我的人.恨我的人.以及对我冷漠的人。 爱我的人教我温柔；恨我的人教我谨慎；对我冷漠的人教我自立。――[J·E·丁格] 98.过去的事已经一去不复返。聪明的人是考虑现在和未来，根本无暇去想过去的事。――[英国哲学家培根] 99.真正的发现之旅不只是为了寻找全新的景色，也为了拥有全新的眼光。――[马塞尔· 普劳斯特] 100.这个世界总是充满美好的事物，然而能看到这些美好事物的人，事实上是少之又少。――[罗丹] 101.称赞不但对人的感情，而且对人的理智也发生巨大的作用，在这种令人愉快的影响之下，我觉得更加聪明了，各种想法，以异常的速度接连涌入我的脑际。――[托尔斯泰] 102.人生过程的景观一直在变化，向前跨进，就看到与初始不同的景观，再上前去，又是另一番新的气候――。[叔本华] 103.为何我们如此汲汲于名利，如果一个人和他的同伴保持不一样的速度，或许他耳中听到的是不同的旋律，让他随他所听到的旋律走，无论快慢或远近。――[梭罗] 104.我们最容易不吝惜的是时间，而我们应该最担心的也是时间；因为没有时间的话，我们在世界上什么也不能做。――[威廉· 彭] 105.人类的悲剧，就是想延长自己的寿命。我们往往只憧憬地平线那端的神奇【违禁词，被屏蔽】，而忘了去欣赏今天窗外正在盛开的玫瑰花。――[戴尔· 卡内基] 106.休息并非无所事事，夏日炎炎时躺在树底下的草地，听着潺潺的水声，看着飘过的白云，亦非浪费时间。――[约翰· 罗伯克] 107.没有人会只因年龄而衰老，我们是因放弃我们的理想而衰老。年龄会使皮肤老化，而放弃热情却会使灵魂老化。――[撒母耳· 厄尔曼] 108.快乐和智能的区别在于：自认最快乐的人实际上就是最快乐的，但自认为最明智的人一般而言却是最愚蠢的。――[卡雷贝· C· 科尔顿] 109.每个人皆有连自己都不清楚的潜在能力。无论是谁，在千钧一发之际，往往能轻易解决从前认为极不可能解决的事。――[戴尔· 卡内基] 110.每天安静地坐十五分钟· 倾听你的气息，感觉它，感觉你自己，并且试着什么都不想。――[艾瑞克· 佛洛姆] 111.你知道何谓沮丧---就是你用一辈子工夫，在公司或任何领域里往上攀爬，却在抵达最高处的同时，发现自己爬错了墙头。－－[坎伯] 112.「伟大」这个名词未必非出现在规模很大的事情不可；生活中微小之处，照样可以伟大。――[布鲁克斯] 113.人生的目的有二：先是获得你想要的；然后是享受你所获得的。只有最明智的人类做到第二点。――[罗根· 皮沙尔· 史密斯] 114.要经常听.时常想.时时学习，才是真正的生活方式。对任何事既不抱希望，也不肯学习的人，没有生存的资格。 ――[阿萨· 赫尔帕斯爵士] 115.旅行的精神在于其自由，完全能够随心所欲地去思考.去感觉.去行动的自由。――[威廉· 海兹利特] 116.昨天是张退票的支票，明天是张信用卡，只有今天才是现金；要善加利用。――[凯· 里昂] 117.所有的财富都是建立在健康之上。浪费金钱是愚蠢的事，浪费健康则是二级的谋杀罪。――[B·C·福比斯] 118.明知不可而为之的干劲可能会加速走向油尽灯枯的境地，努力挑战自己的极限固然是令人激奋的经验，但适度的休息绝不可少，否则迟早会崩溃。――[迈可· 汉默] 119.进步不是一条笔直的过程，而是螺旋形的路径，时而前进，时而折回，停滞后又前进，有失有得，有付出也有收获。――[奥古斯汀] 120.无论那个时代，能量之所以能够带来奇迹，主要源于一股活力，而活力的核心元素乃是意志。无论何处，活力皆是所谓“人格力量”的原动力，也是让一切伟大行动得以持续的力量。――[史迈尔斯] 121.有两种人是没有什么价值可言的：一种人无法做被吩咐去做的事，另一种人只能做被吩咐去做的事。――[C·H·K·寇蒂斯] 122.对于不会利用机会的人而言，机会就像波浪般奔向茫茫的大海，或是成为不会孵化的蛋。――[乔治桑] 123.未来不是固定在那里等你趋近的，而是要靠你创造。未来的路不会静待被发现，而是需要开拓，开路的过程，便同时改变了你和未来。――[约翰· 夏尔] 124.一个人的年纪就像他的鞋子的大小那样不重要。如果他对生活的兴趣不受到伤害，如果他很慈悲，如果时间使他成熟而没有了偏见。――[道格拉斯· 米尔多] 125.大凡宇宙万物，都存在着正、反两面，所以要养成由后面.里面，甚至是由相反的一面，来观看事物的态度――。[老子] 126.在寒冷中颤抖过的人倍觉太阳的温暖，经历过各种人生烦恼的人，才懂得生命的珍贵。――[怀特曼] 127.一般的伟人总是让身边的人感到渺小；但真正的伟人却能让身边的人认为自己很伟大。――[G.K.Chesteron] 128.医生知道的事如此的少，他们的收费却是如此的高。――[马克吐温] 129.问题不在于：一个人能够轻蔑、藐视或批评什么，而是在于：他能够喜爱、看重以及欣赏什么。――[约翰· 鲁斯金]

C．轮船招商局的轮船
D．福州船政局的军舰
[解析]
由材料信息“19世纪七十年代，由江苏沿江居民
到上海”可判断最有可能是轮船招商局的轮船。 [答案] C
[题组冲关] 1．中国近代史上首次打破列强垄断局面的交通行业是 ( )
A．公路运输
C．轮船运输
B．铁路运输
D．航空运输
解析：根据所学1872年李鸿章创办轮船招商局，这是洋务 运动中由军工企业转向兼办民用企业、由官办转向官督商 办的第一个企业。具有打破外轮垄断中国航运业的积极意 义，这在一定程度上保护了中国的权利。据此本题选C项。 答案：C
台湾 架设第一条电报线，成为中国自
出行 (1)新式交通促进了经济发展，改变了人们的通讯手段和 ， 方式 转变了人们的思想观念。
(2)交通近代化使中国同世界的联系大大增强，使异地传输更为便 捷。 (3)促进了中国的经济与社会发展，也使人们的生活
多姿多彩 。
[合作探究· 提认知]
电视剧《闯关东》讲述了济南章丘朱家峪人朱开山一家， 从清末到九一八事变爆发闯关东的前尘往事。下图是朱开山 一家从山东辗转逃亡到东北途中可能用到的四种交通工具。
依据材料概括晚清中国交通方式的特点，并分析其成因。
提示：特点：新旧交通工具并存(或：传统的帆船、独轮车， 近代的小火轮、火车同时使用)。 原因：近代西方列强的侵略加剧了中国的贫困，阻碍社会发 展；西方工业文明的冲击与示范；中国民族工业的兴起与发展；
政府及各阶层人士的提倡与推动。
[串点成面· 握全局]
A
[题组冲关] 3．假如某爱国实业家在20世纪初需要了解全国各地商业信
息，可采用的最快捷的方式是
(
)
A．乘坐飞机赴各地了解 B．通过无线电报输送讯息 C．通过互联网 D．乘坐火车赴各地了解

有何关系？
2024/10/13
思考 :怎样由y sin x的图象得到y 2sin(1 x )
36 的图象?
(1)向右平移
函数y sin x
6
y sin( x )的图象
6
(2)横坐标伸长到原来的3倍 y sin(1 x )的图象
纵坐标不变
36
(3)纵坐标伸长到原来的2倍 y 2sin(1 x )的图象
y
2
y=2sinx
1
y=sinx
2
O
1
y=
1sinx
2 2
yx 2
1
2024/10/13
O
1
2
2 x
一、函数y=Asinx(A>0)的图象
2024/10/13
y
y=2sinx
2
1
O
1 y= 1sinx
2
2
2 x
函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时) 或缩短(当0<A<1时) 到原来的A倍(横坐标不变) 而得到的。 y=Asinx ，x∈R的值域为[-A,A]，最 大值 为A，最小值为-A.
新课讲解:
例1 作函数
y 2sin x
及
y
1 sin 2
x
的图象。
解：1.列表
x
0
2
3 2
2
sin x
0
1
0
1
0
2sin x 0
2
0
2
0
1 2
sin
x
0
1 2
0
1 2
0

问题情境 根据正弦函数的定义可知，任意给定一个角α，唯
一确定一个正弦值 sinα.习惯上，我们用x表示角α的弧 度数（自变量）, y 表示因变量，于是正弦函数可记作
y = sinx, x∈R , 其中x表示角的弧度值函数的定义域是实数集 R .
调动思维，探究新知 在在活初初动中中2，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
情感目标 通过本节课学习，使学生养成乐于学习、勇于探索的良好品质
核心素养
通过思考、讨论等活动，提升学生数学的直观想象、逻辑推理、数据分析、 数学建模的核心素养
创设情境，生成问题 在在活初初动中中1，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
2．正弦函数的性质 探索研究
观察单位圆中的正弦线（图5-24）或正弦函数的图 象，你发现正弦函数有哪些性质？
调动思维，探究新知 在活初动中2，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
（1）值域
因为在单位圆中，正弦线的长都小于或等于半径的
长1，所以 sin x 1即-1≤sin x≤1，这就是说，正弦函
数学
基础模块（上册）
第五章 三角函数
5.3.1正弦函数的图象和性质
人民教育出版社
第五章 三角函数 5.3.1 正弦函数的图象和性质
学习目标
知识目标 理解正弦曲线的概念，认识正弦函数的图象及正弦函数图象的研究方法
能力目标

波形
正弦函数的图像呈现出典 型的波形，即一个连续的 、重复的曲线。
图像的周期性与振幅
周期性
正弦函数的周期性意味着我们可以使用一个常数（通常称为相位偏移量）来移动 函数的图像，而不改变其形状或特性。这个常数被称为相位偏移量，通常用希腊 字母表示。
振幅
正弦函数的振幅是指函数值可以变化的范围。振幅的大小可以用数学公式表示， 也可以在图像上直观地看到。
要点二
控制系统
正弦函数经常用于分析和设计控制系统，如反馈控制系 统和自动控制系统。在控制工程中，正弦函数被用于描 述和建模系统的动态行为。
在数学与其他领域中的应用
微积分
正弦函数是微积分中重要的函数之一。它在求解微分方 程、最优控制和最优化问题等数学问题中具有广泛的应 用。
统计学
正弦函数在统计学中也有应用，如在描述正态分布的尾 部概率密度函数时。此外，正弦函数还被用于信号处理 和图像处理等领域。
图像的极值与零点
极值
正弦函数在某些点上达到最大或最小值。这些点称为极值点 。在图像上，极值点通常表现为曲线向上或向下突然转折的 点。
零点
正弦函数在某些点上为零。这些点称为零点。在图像上，零 点通常表现为水平线段，即函数值为零的点。
03
正弦函数的性质
函数的单调性
递增区间
正弦函数在$\lbrack - \frac{\pi}{2} + 2k\pi,\frac{\pi}{2} + 2k\pi\rbrack(k \in \mathbf{Z})$上单调 递增。
正弦函数与反正弦函数的关系
反正弦函数（asin）是正弦函数的反函数。 它的定义域和值域与正弦函数相反。
反正弦函数和正弦函数在图像上呈现对称性 ，且具有相同的频率但相位不同。

上都单调递减，其值从1减小到-1.
最大值与最小值
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到：

+ ( ∈ ) 时取得最大值1，


当且仅当 = − + ( ∈ ) 时取得最小值-1；

①正弦函数当且仅当 =
②余弦函数当且仅当 = ( ∈ ) 时取得最大值1，
【1】周期性：观察正弦函数的图像，可以发现，在图像上，横坐标每隔2π个单位
长度，就会出现纵坐标相同的点，这就是正弦函数值具有的“周而复始”的
变化规律.实际上，这一点既可以从定义中看出，也能从诱导公式中得到反映.即自
变量 的值加上2π的整数倍时所对应的函数值，与 所对应的函数值相等.数学
上用周期性来定量地刻画这种“周而复始”的规律.
如何用自变量的系数表示上述函数的周期呢？
事实上，令 = + ，那么由 ∈ 得 ∈ ，且函数 = , ∈ 及函数
= , ∈ 的周期都是.
因为 + = + + = +




+ ，所以自变量增加 ，函数值




+ ,
+ ( ∈ ) 上都单调递减，其值从1减小到-1.


单调性


−
−



−



同样的道理结合余弦函数的周期性我们可以知道：
余弦函数在每一个闭区间
在每一个闭区间
− + , ( ∈ ) 上都单调递增，其值从-1增大到1；
, + ( ∈ )
关于y轴对称.所以正弦函数是奇函数，余弦函数是偶函数.

思考1：观察下列正弦曲线和余弦曲线的
对称性，你有什么发现？
y 1y=sinx-π-4π-2π
-5π -3π
-π
π
3π
5π
x
O
2π
4π
6π
-1
y y=cosx
2
2
1 22

2
2
x
2

O
2
2-1
2


2
2 40
思考2：上述对称性反映出正、余弦函数 分别具有什么性质？如何从理论上加以 验证？ 正弦函数是奇函数，余弦函数是偶函数.
-6π
-4π
-2π
-5π -3π
y 1
-π
π
O
-1
3π
5π
2π
4π
6π x
9
思考8：你能画出函数y=|sinx|， x∈[0，2π ]的图象吗？
y 1
O
π
-1
2π x
10
知识探究（二）：余弦函数的图象
思考1：观察函数y=x2与y=(x＋1)2 的图 象，你能发现这两个函数的图象有什么 内在联系吗？
18
10
(2) cos( 23)与cos( 17).
5

例3 求函数 y sin( 1 x ，)
23
x∈[－2π ，2π ]的单调递增区间.
50
小结作业
1. 正、余弦函数的基本性质主要指周期 性、奇偶性、单调性、对称性和最值， 它们都是结合图象得出来的，要求熟练 掌握.
作业：P36练习：1，2，3.
35
1.4.2 正弦函数、余弦函数的性质 第二课时

知识梳理
注意点： (1)关键词“每一个x”体现了对定义域中每一个值都得成立. (2)周期函数的周期不唯一，任何T的非零整数倍都是函数的周期. (3)三角函数的周期是函数的整体性质，我们在研究函数时，只需研究一 个周期上的图象和性质即可. (4)若不加特殊说明，一般求三角函数的周期的问题，求的是函数的最小 正周期.
反思感悟
(1)定义法求函数的周期：紧扣周期函数的定义，寻求对定义域内的任意 x都满足f(x＋T)＝f(x)的非零常数T，该方法主要适用于抽象函数. (2)定义法判断函数的奇偶性：从f(－x)的解析式中拼凑出f(x)的解析式， 再依据f(－x)＝－f(x)或f(－x)＝f(x)来判断.
跟踪训练1 (1)函数y＝|sin x|，x∈R的最小正周期为__π__.
(2)判断等式 sin－π3＋53π＝sin－π3是否成立？如果成立，能否说明53π是函 数 y＝sin x 的周期？
sin－π3＋53π＝sin 43π＝sinπ＋π3＝－sin π3， 而 sin－π3＝－sin π3，
所以上述等式成立， 但不能说明53π是函数 y＝sin x 的周期， 理由如下，若53π是函数 y＝sin x 的周期， 则对任意的实数 x，都有 sinx＋53π＝sin x， 但当 x＝0 时，sinx＋53π≠sin x，所以53π不是函数 y＝sin x 的周期.
设f(x)＝|sin x|， ∵f(x＋π)＝|sin(x＋π)|＝|sin x|＝f(x)， ∴y＝|sin x|的最小正周期为π.
(2)函数f(x)＝xsin(π＋x) A.是奇函数，但不是偶函数
√B.是偶函数，但不是奇函数
C.既是奇函数，又是偶函数 D.既不是奇函数，也不是偶函数
易知函数f(x)的定义域R关于原点对称， ∵f(x)＝xsin(π＋x)＝－xsin x， f(－x)＝(－x)sin(π－x)＝－xsin x＝f(x)≠－f(x)， ∴f(x)是偶函数，不是奇函数.

信号处理
在信号处理领域，正弦函数常被用 于信号的滤波、调制和解调等操作。
机械工程
在机械振动和噪音控制中，正弦函 数被用于描述和分析振动模式和频 率。
在日常生活中的应用
音乐
正弦函数在音乐领域的应 用非常广泛，如音高和音 长的计算等。
通信
无线电和电视信号的传输 过程中，正弦函数用于调 制和解调信号。
医学成像
正弦函数的周期性
总结词
正弦函数具有周期性，即函数图像每 隔一定周期重复出现。
详细描述
正弦函数的周期为360度或2π弧度，这 意味着每经过360度或2π弧度，函数值 会重复之前的值，形成周期性的波形。
正弦函数的奇偶性
总结词
正弦函数是奇函数，具有奇函数的性质。
详细描述
奇函数满足性质f(-x)=-f(x)，对于正弦函数，当取相反角度时，函数值也取相反 数。例如，sin(-π/2) = -1，与sin(π/2)的值相反。
03
正弦函数的应用
在物理中的应用
01
02
03
简谐振动
正弦函数是描述简谐振动 的基本函数，如弹簧振荡 器、单摆等。
交流电
正弦函数被广泛用于描述 交流电的电压、电流和频 率，是电力系统的基本模 型。
声学
声音的传播和波动可以用 正弦函数来描述，如声波 的振幅和频率。
在工程中的应用
控制系统
正弦函数在控制系统分析中有着 广泛应用，如PID控制器等。
03
奇偶性
正弦函数是奇函数，而正切函数是奇函数。这意味着它们在对称性上有
相同的表现。
与其他三角函数的比较
定义域
除了正弦函数、余弦函数和正切函数外，还有其他一些三角函数，如反正弦函数、反余弦 函数、反正切函数等。它们的定义域各不相同，但都与正弦函数、余弦函数和正切函数的 定义域有交集。