当前位置：文档之家 › 弹性与塑性力学基础-第四章广义虎克定律和弹性力学解题只是分享

弹性与塑性力学基础-第四章广义虎克定律和弹性力学解题只是分享

  • 格式：ppt
  • 大小：1.67 MB
  • 文档页数：95

下载文档原格式

  / 95

合集下载

弹塑性力学第四章答案

弹塑性力学第四章答案

第四章 习题答案4.3有一块宽为a ，高为b 的矩形薄板，其左边及下边受链杆支承，在右边及上边分别受均布压力1q 和2q 作用，见题图4.1，如不计体力，试求薄板的位移。

题图4-1解：1.设置位移函数为123123()()u x A A x A y v y B B x B y =+++⎫⎬=+++⎭（1）因为边界上没有不等于零的已知位移，所以式00,m m m m mmu u A u v v A v =+=+∑∑中的0u 、0v 都取为零，显然，不论式（1）中各系数取何值，它都满足左边及下边的位移边界条件，但不一定能满足应力边界条件，故只能采用瑞兹法求解。

2.计算形变势能。

为简便起见，只取1A 、1B 两个系数。

111111,u A x Au v B y B v ==== （2） 11,0,,0uuvu A B x yyx∂∂∂∂====∂∂∂∂ ()()2222111111112200222(1)2(1)a b E Eab U A B A B dxdy A B A B v v νν=++=++--⎰⎰ （3） 3.确定系数1A 和1B ，求出位移解答。

因为不计体力()0X Y ==，且注意到1m =，式4-14简化为11UXu ds A ∂=∂⎰ （4）11UYv ds B ∂=∂⎰ （5） 对式（4）右端积分时，在薄板的上下边和左边，不是0X =，就是10u =，故积分值为零。

在右边界上有11,,X q u x a ds dy =-===()111bXu ds q ady q ab =-=-⎰⎰ （6）同理，式（5）右端的积分只需在薄板的上边界进行，()1220aYv ds q bdx q ab =-=-⎰⎰ （7）将式（3）、式（6）、式（7）分别代入式（4）、式（5）可解出1A 和1B ：()1112222(1)EabA B q ab v ν+=---()1122222(1)EabB A q ab v ν+=--- 121q q A E ν-=-， 211q q B E ν-=- （8） 122111,q q q q u A x x v B y y E Eνν--==-==- （9）4．分析：把式(8)代入几何和物理方程可求出应力分量，不难验证这些应力分量可以满足平衡微分方程和应力边界条件，即式(8)所示位移为精确解答。

广义虎克定律

广义虎克定律

12 广义虎克定律在弹性力学中，我们由弹性变形过程是一个可逆过程这个前提出发，依据热力学分析，得到了应力分量ij σ是应变分量ij ε的单值函数的结论. 加上小变形的假设，可将应力按泰勒展开，并略去二阶及二阶以上的高阶小量. 我们还假定物体未变形时内部没有应力，得到kl ijkl ij c εσ= (12-1)式中ijkl c 称为广义弹性常数. (12-1)式也可以写成kl ijkl ij b σε= (12-2)式中ijkl b 称为柔性系数.13 各向同性物体的广义虎克定律13.1 一般的表示(12-1)式中ijkl c 为一个四阶张量，共81个元素. 由于形变张量是对称的，所以将指标i 与j , k 与l 互易，或将i ,j 与k ,l 成对地互易之后，乘积kl ij εε并不改变. 由此可见，张量ijkl c 也可以有这个性质，即当指标互易时具有如下的对称性质:klij ijlk jikl ijkl c c c c === (13-1)经计算可证实，四阶张量的分量中具有以上对称性质的分量，在一般情形中有21个. 因此，对极端各向异性的材料，也只有21个独立的弹性常数. 至于具有三个正交的弹性对称面的物体，则具有9个独立的弹性常数，这样的物体称为正交各向异性体. 正交各向异性体的弹性系数矩阵具有如下的形式：⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛665544332322131211000000000000c c c c c c c c c 对称对于各向同性体，利用坐标轮换时应变能的不变性和坐标轴选取的任意性可以证明，独立的弹性常数减少到只有2个.各向同性材料的弹性常数矩阵为⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+++G G G G G G000000200020002对称λλλλλλ广义虎克定律可写为.2,2,2,2,2,2121233333131222223231111εσλθεσεσλθεσεσλθεσG G G G G G =+==+==+= (13-2) 或者简写为ij ij ij G λθδεσ+=2 (13-3)其中u div 321332211=++=++==εεεεεεεθii 为体积应变或应变张量的第一不变量，ij δ为Kroneker 符号.广义虎克定律也可以写成以应力分量表示应变分量的形式：⎥⎦⎤⎢⎣⎡⋅⋅+-=ij ij ij I G G δλλσε1)23(21 (13-4) 其中3322111σσσσ++==Θ=ii I 为应力张量的第一不变量.13.2 弹性常数及其相互之间的关系常用的弹性常数有λ、G 、E 、μ、K . 其中λ和G 称为拉梅常数，G 又称为剪切模量或刚性模量. E 称为杨氏弹性模量，μ称为泊松比或横向变形系数，K 称为体积弹性模量.G 可以利用纯剪切试验直接测得， 此时τσ=12， 其余应力分量均为零，根据(13-2),G 2/12τε=. 因此测得τ和12ε即可求得G.E 和μ可以利用单轴拉伸试验测得，此时σσ=11，其余0312*******=====σσσσσ.令11111σEε=， 11113322σE εεεμμ-=⋅-== (13-5)由广义虎克定律(13-2)⎪⎪⎪⎭⎫+=+=+=λθελθελθεσ3322111120202G G G (13-6) 将上三式相加得到)2G 3/(11+=λσθ将上式代入(13-6)的第一式得到GG G E ++=λλ)23( (13-7)代入(13-6)的第二式或第三式得到)(2G +=λλν (13-8)(13-7)、(13-8)也可以化为)21)(1(μμμλ-+=E ， )1(2μ+=EG (13-9)利用(13-9)可将虎克定律表示为如下更常用的形式[][][]）（））（2211333311332222332211111(11σσμσεσσμσεσσμσε+-=+-=+-=EE E ⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+=+=121231312323111σμεσμεσμεE E E(13-10)或ij ij ij EE δσμσμε031-+=(13-11) 其中3/3/3/)(13322110I =Θ=++=σσσσ，1I 为应力张量第一不变量，ij δ为Kroneker 符号.在各向均匀压力试验中，p -===332211σσσ, 0312312===σσσ, 将上述应力分量的值代入广义虎克定律公式(13-2)得到λθε+=-112G p ， λθε+=-222G p λθε+=-332G p将上面三式相加就得到θλ)23(3G p +=-定义体积变形模量K 为θ/p K -=就得到G K 32+=λ (13-12)可推出五个弹性常数之间的关系, 结果如下：,9)3(313 )21)(1(323)2(212EK E K K K E G K E G G E G G --=+=-+=-=--=-=μμμμμμμλE K KEK E K G -=+-=+=-=-=93)1(2)21(3 )1(2)(232)21(μμμλμμλ KEK G K G K G E K G 63)3(223 123)(2-=+-=-=-=+=μλλλμ )21(339)1(2 3)(9)21)(1()23(μμλλμμμλλλ-=+=+=--=-+=++=K GK KG G K K K G G G E.)21(3)3(3 )21(3)1(23)1(32μμμμμλλ-=-=-+=+=+=EE G GE G G K (13-13).12+ ,21μμλλμλ-=-=+G G G (13-14)。

弹塑性力学(4)

弹塑性力学(4)
弹性力学土木工程学院许强第四章弹性应力应变关系414243444546474849410411412413引言基本假设假定建立弹性材料模型的必要性定义各向同性材料的线弹性应力应变关系虚功原理弹性固体的应变能和余能密度各向异性线弹性体应力应变关系非线弹性应力应变关系弹性体的唯一性稳定性正交性和外凸性各向同性材料的增量应力应变关系基于割线模量的增量关系变模量增量应力应变模型第四章弹性应力应变关系前面已进行了应力分析和应变分析导出了平衡方程和几何方程
2. 由于真实的位移场（应变场）必须满足位移边界条件，故真实位移场（应 变场）应视为可能位移场（应变场）的家族成员之一。而对于真实位移场 （应变场）还必须满足“应变协调条件”，即应变可积分条件。 3. 一般而言，与满足位移边界条件的连续变形相协调的位移模式有无限多个。 但对于给定的问题，同时又满足应变协调的位移模式仅存在一个，即真实 位移场仅有一个。 4. 在弹性力学问题的求解思路通常有两种：（a）按应力求解，（b）按位移 求解。而仅当按应力求解时才用到应变可积分条件，即式（4.2b）。
§4.4 定义
弹性材料
当一块材料受力后就会变形，如果施加的力撤除后，物体即恢复它原来的形状和 大小，那么这种材料就可称为弹性的。从数学上来说，这种材料的本构方程为：
σij = Fij (εkl )
(4.3)
其中， Fij为弹性响应函数，因此，由上式描述的弹性性能为既可逆又与路 径无关，即应变仅由当前应力状况所决定，反之亦然。上述定义的弹性材 料通常称为Cauchy弹性材料。 在特定的加载－卸载循环下，Cauchy弹性材料可产生能量，显然这是 与热力学定律相违背的。为此，采用术语超弹性或Green弹性材料去表明 式（4.3）中的弹性影响函数进一步受到弹性应变能函数W存在的限制。 一般而言，W是应变分量的函数，即

弹塑性力学第四章

弹塑性力学第四章

代入广义胡克定律
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
c11 x c12 y c13 z c14 xy c15 yz c16 zx
b
广义胡克定律
由应力分量的坐标变换公式（2-20）可得：
广 西 工 学 院 汽 车 工 程 系
xy l11l22 xy xy 2 x l11 x x 2 y l22 y y 2 z l33 z z
上述关系式是胡克（Hooke）定律在复杂应力条件下 的推广，因此又称作广义胡克定律。
广义胡克定律
广义胡克定律的张量表示： ij cijkl kl cijkl 称为弹性系数，一共有36个。
i, j, k , l 1, 2.3
广 西 工 学 院 汽 车 工 程 系
如果物体是非均匀材料构成的，物体内各点受力后将 有不同的弹性效应，因此一般的讲，cmn 是坐标x，y，z 的函数。 如果物体是由均匀材料构成的，那么物体内部各点， 如果受同样的应力，将有相同的应变；反之，物体内各 点如果有相同的应变，必承受同样的应力。 因此cmn为弹 性常数，与坐标无关。 各向同性材料，独立的弹性常数只有两个。
xy yz zx
xy
G
yz
G
zx
G
式中， G
E 2 1 v
为各向同性物体的剪切弹性模量。
表示材料弹性性能的常数有3个，但只有两个是独立的。 张量记法：
1 v v ij ij E E vE ij e E ij ij 1 v 1 v 1 2v

弹塑性力学第四章

弹塑性力学第四章

若通过物体每一点可作这
样的轴（如x3轴），在此轴 成垂直的平面内，所有射
线方向的弹性性质都是相
同的，称这个平面为各向
同性面，如地层属于此类。
[C]中独立系数为5个：
x1
x3 x2’
x2Fra bibliotek各向同性面
x1’
2019/10/18
28
§4-2 线弹性体的本构关系
2.4 横观各向同性材料——弹性体对一个轴对称
ij
2019/10/18
12
§4-1 应变能、应变能密度与弹性材料的
本构关系
W ijij
比较上面二式，得：
W

W
ij
ij
ij

W
ij

fij ( kl )——本构关系（方程）
适用于各种弹性情况（线性、非线性）
2019/10/18
13
§4-1 应变能、应变能密度与弹性材料的 本构关系
本构关系
时刻达到 应变增量
t
+t：位移有增量 u

ijeie j

uiei
外力功增量 ：


A V f udV SF udS
2019/10/18
8
§4-1 应变能、应变能密度与弹性材料的
本构关系


：函数增量

A V f udV SF udS
WdV
V
S Fi uidS S (ij ui )njdS V ( ji ui ), j dV
代入外力功增量
2019/10/18
10
§4-1 应变能、应变能密度与弹性材料的 本构关系

广义胡克定律

广义胡克定律

第四章 广义胡克定律第四章 广义胡克定律 (1)§4.1节广义胡克定律 (2)§4.2节拉梅常数与工程弹性常数 (5)§4.3节弹性应变能函数 (7)§4.1节 广义胡克定律（一）单向应力状态下胡克定律单向应力状态下，处于线弹性阶段材料，其应力与应变关系可由下式表示：x x E σε=其中E 为材料的弹性模量。

（二）三维广义胡克定律三维条件下，物体应力状态可由6个分量表示，而应变状态也由6个分量表示。

假设应力与应变的各个分量之间均相关，一般地，1111111222133314121523163122211122222333241225232631333111322233333412352336311241114222433344124523463123511152225c c c c c c c c c c c c c c c c c c c c c c c c c c c σεεεεεεσεεεεεεσεεεεεεσεεεεεεσεε=+++++=+++++=+++++=+++++=++33354125523563131611162226333641265236631c c c c c c c c c εεεεσεεεεεε⎧⎪⎪⎪⎪⎨⎪⎪+++⎪=+++++⎪⎩ 或写作111213141516111121222324252622223132333435363333121241424344454623235152535455563131616263646566c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c σεσεσεσεσεσε⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥⎥ 其中，mn C （,1,,6m n ="）为弹性常数。

弹塑性力学 弹性与塑性力学的解题方法

既能找出变形体中各点的应力分量，也能找出相 对的位移增量分量。
➢主应力法
➢ 主应力法是金属塑性成形中所经常使用的 一种简化方法。在分析问题时，认为剪应 力对材料的屈服影响很小，因而在屈服条 件中略去剪应力，这时平面应变问题中的 屈服条件可简化为
x - y = 2k
➢ 在分析中，还假设应力在一个方向的分布 是均匀的。因此在计算中，数学形式比较 简便。
➢ 平面应力问题，平面应变问题，结果转换 ➢ 平面问题的平衡方程（无体力）
x
xy
0
x y
yx x
y
y
0
➢ 艾里（Airy）应力函数
x
2
y 2
,
y
2
x 2
,
xy
2
xy
➢ 用应力函数表示的物理方程
➢ 变形协调条件
x
1 2G(1
)
2
y 2
2
x 2
y
2G
1 (1
)
2
x 2
几种应力函数所对应的边界条件
➢ = ax + by + c 矩形弹性体处于无应力状态，
即在边界上无面力。
➢ = ax2 + bxy + cy2 矩形弹性体受双向荷载。
a > 0, c > 0, b = 0
a = c = 0, b 0
➢ = ax3 + bx2y + cxy2 + dy3 复杂应力状态， 当a = c = b = 0, d 0时，xy = 6dy，为纯弯
2
y 2
xy
1 G
2
xy
4 x
y 4
4 y
x 4

第四章广义胡克定律


式中共有 36 个常数。
（三）弹性常数矩阵的对称性
上述 36 个常数并不都是独立的，从§4.3 节能量角度考虑，弹性常数矩阵是对称的，即极端
2
弹性力学讲义（2013 版），山东大学岩土中心 王者超
各向异性的弹性体其独立弹性常数只有 21 个。 根据材料本身性质的对称性，独立的弹性常数个数将发生变化。 若材料具有一个对称面，则弹性常数减少至 13 个； 若材料具有三个正交的对称面，即材料具有正交各向异性，则弹性常数减少至 9 个； 若材料是横观各向同性的，则弹性常数减少至 5 个； 最后，若材料是各向同性的，则弹性常数只有 2 个。
+
c24ε
′
12
+
c25ε
′
23
+
c26ε
′
31
⎪⎪σ ⎨
′
33
=
c31ε
′
11
+
c32ε
′
22
+
c33ε
′
33
+
c34ε
′
12
+
c35ε
′
23
+
c36ε
′
31
⎪σ ⎪
′
12
=
c41ε
′
11
+
c42ε
′
22
+
c43ε
′
33
+
c44ε12′
+
c45ε
′
23
+
c46ε
′
31
⎪σ ⎪
′
23
=
c51ε11′
1
弹性力学讲义（2013 版），山东大学岩土中心 王者超

4-弹塑性力学-物理方程与边界条件

பைடு நூலகம்
�
第四章 物理方程与边界条件
求和约定(The arrnagement for summation) 求和约定
例3 将y1 = εijδij 按求和约定展开. 和y2 = σijεijδij (i, j =1,2,3) 按求和约定展开.
i 为克氏符号, 为克氏符号,= j, δ ij = 1; i ≠ j, δ ij = 0.
1 E
1 E 其中E, , 分别为各向同性材料的弹性模量, 其中 ,G, 分别为各向同性材料的弹性模量,泊松比和剪切弹性 模量,并有: 模量,并有: E
ε z = [σ z (σ x + σ y )],
G =
1 1 ε xy = γ xy = τ xy 2 2G 1 1 ε yz = γ yz = τ yz 2 2G 1 1 ε zx = γ zx = τ zx 2 2G
2 (1 + )
可见,各向同性材料只有两个独立的弹性常数. 可见,各向同性材料只有两个独立的弹性常数.
第四章 物理方程与边界条件
思考题: 思考题:
1. 如何将三维广义虎克定律写成应力对应变的函数? 如何将三维广义虎克定律写成应力对应变的函数? 2.何将广义虎克定律写成矩阵的形式? .何将广义虎克定律写成矩阵的形式? ) {σ } = C {ε },或{ε } = S {σ }(i,j,k,l = x,y,z)
ij ijkl kl ij ijkl kl
其中 Cijkl 称为刚度矩阵,Sijkl 称为柔度矩阵. 称为刚度矩阵, 称为柔度矩阵.
第四章 物理方程与边界条件
体积应变
由广义虎克定律
三式相加,则有 三式相加 则有
1 [σ x (σ y + σ z )] E 1 ε y = [σ y (σ z + σ x )] E 1 ε z = [σ z (σ x + σ y )] E

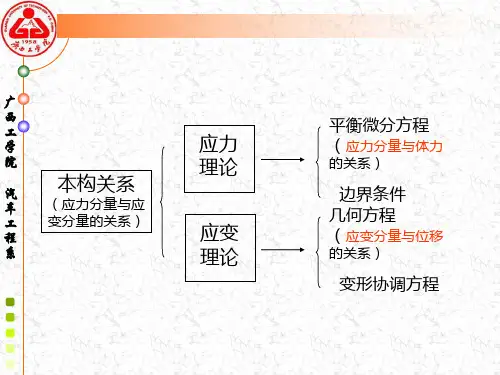
弹塑性力学第四章


y c21 x c22 y c23 z z c31 x c32 y c33 z
x 对 x 的影响应与 y 对 y 及 z 对 z 的影响相同，即 c11 c22 c33
y , z 对 x 的影响应相同，即 同理，
因而有：
c12 c13
c11 c22 c33 a c12 c21 c13 c31 c23 c23 b
对于应变主轴，弹性常数只有两个。
广义胡克定律
各向异性弹性体独立的常数有21个。 系数矩阵对称 Cmn Cnm 广 西 工 具有一个弹性对称面的各向异性弹性体的独立常数有13个。 学 院
广义胡克定律
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院 汽 车 工 程 系
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院
x 汽 x 车 工 2 2 2 x l11 y l12 z l13 2 xy l11l12 yz l12l13 xz l11l13 x x 程 系 ,
y y z z
z
y
y
z
ij liil jj ij
车 工 程 系
弹性对称面：如果物体内存在这样一个平面，和该平面对称的 汽 两个方向都具有相同的弹性，则该面称为物体的弹性对称面。 弹性主方向：垂直于弹性对称面的方向 具有三个弹性对称面的各向异性弹性体（正交各向异性）的 独立常数有9个。
广义胡克定律
证明：正交各向异性弹性体的独立常数有9个。 证明：取弹性主轴为三个坐标轴，将z轴旋转180度
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如引用=
E (1)(12)
并注意到 2G E
他的关系式，归纳如下
x 2Gx y 2Gy z 2Gz
xy Gxy yz Gyz zx Gzx
(4-8)
称为拉梅(Lamé)弹性常数。用体积应变表示应力时则有
xy
xy
G
式中，G E 2(1 )
为剪切弹性模量
纯剪应力状态
7
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.3 广义胡克定律
➢ 用相同的方法，可以导 出三维应力状态下的各
向同性均匀材料的广义 胡克定律，其形式为：
（各向同性均匀材料的 含义，即材料内部各处 的不同方向具有相同的 μ、E、G 值）
ez 1Ez 21Gz
11
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.4 广义胡克定律的不同形式
ex 1Ex 21Gx ey 1 Ey 21Gy
ez 1Ez 21Gz
➢ 因此，弹性阶段应力莫尔圆和应变莫尔圆是成比例的，因为：
ex ey ez xy yz zx1 x y z 2xy 2yz 2zx 2G
xE 1[xx(xyz)]
即得式(4-6)的第一式 x E 1[1()x]
利用式(4-5) 便可得
12
E
将其代入式(4-6)
xE 1[1()x(1E 2)]
由上式可得
x 1Ex(1)(1E2)
13
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.3 广义胡克定律的不同形式
(4-7)
➢ 弹性阶段应力主轴和应变主轴重合（注意：应力或应变球张量对
应力主轴或应变主轴无影响）
12
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.3 广义胡克定律的不同形式
➢ 各向同性体的胡克定律(4-4)是以应力表示应变，在求解某些问题
时，有时需要用应变表示应力关系。将式(4-4)第一式作如下改变
xy z E 1 [( xyz) 2(xyz)]
1E 2(xyz)
如令
x y z 3 0,x y z 3 m
则上式可写为
12
E
或
0 1E2m
(4-5)
(4-5)表明：弹性变形时，体积变化与三个正应力之和即应力张量的
球张量成正比，而与应力偏量无关。
9
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
弹性与塑性力学基础-第四章广 义虎克定律和弹性力学解题
§4-4 按位移求解弹性力学问题 §4-5 按应力求解弹性力学问题 §4-6 平面问题和应力函数 §4-7 圣维南原理 §4-8 叠加原理 §4-9 悬臂梁受均匀分布载荷作用 §4-10 简支梁受均匀分布载荷作用 §4-11 具有小圆孔的平板的均匀拉伸 §4-12 位错引起的应力与弹性应变能
2
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.1 问题的提出 ➢ 弹性力学问题中，物体的受力与变形情况，需用15个变量来 描述。即：6个应力分量，3个位移分量，6个应变分量。
➢ 已学的基本方程－9个。包括：变形体的平衡微分方程（微元 体的力平衡）3个，几何方程（应变－位移关系）6个。
§4-1 广义胡克定律
4.1.4 广义胡克定律的不同形式 ➢ 由式(4-6)及式(4-5)，可得
x
0
1 [(1 E
)x
]
12
E
m
1 [(1 E
)x
3m]
12
E
m
1
E
(x
m)
即：
ex 1Ex 21Gx
式中： ex=x- 0 为应变偏量分量，x xm为应力偏量分量。
用相同的方法，可得：
ey 1 Ey 21Gy
平面双向拉（压）应力
纯剪应力状态
5
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
平
面
2、平面应力状态:
应
力
由于应力x的作用：
时
x方向应变为 x
的 胡
E
克
y方向应变为 x
定 律
E
由于应力y的作用： y方向应变为 y
E
x方向应变为 y E
同时有x和y作用在x方向及y方向的应变为
x y
x
E
y
E
y
E
x
E
E1(x E1(y
y)(4-3)
x)
6
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
2、平面应力状态：
在x和y作用下，z方向的应变
εz= -μ(x＋y)/E
在剪应力作用下， X-Y 平面内的剪 应变与纯剪时相同，即：
➢ 未知变量的个数（15）多于方程数（9）→必须研究受力物体 的应力与应变之间的关系→物理方程。对于弹性问题，即广义 胡克定律。
3
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.2 胡克定律
1、单向拉伸（压缩）：
➢ 材料的应变小于弹性比例极限时，应力和应变之间的关系是线弹 性的，两者之间满足胡克定律。其表达式如下：
拉伸或压缩方向：x =·x 与拉伸或压缩垂直的方向： y = z=-μ·x
式中： －弹性模量， μ－泊松比
4
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
2、平面应力状态:
➢ 对于各向同性的均匀材料，根据实验结果，在小变形的情况下， 正应力和剪应变没有关系，而剪应力只与剪应变有关，且应力的 叠加原理是适用的。
x y
1
E 1
E
[ [
x y
( (
y x
z
)]
z )]
z
1 E
[
z
(
x
y
)]
xy
xy G
yz
yz G
zx
zx G
(4-4)
8
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法
§4-1 广义胡克定律
4.1.4 广义胡克定律的不同形式 ➢ 将式(4-4)的前三式左右两边相加后，则有
§4-1 广义胡克定律
4.1.4 广义胡克定律的不同形式 ➢ 引入以上表达式后，广义胡克定律又可写为：
x
1 E
[(1
) x
],
xy
1 G
xy
y
1 E
[(1
)
y
],
yz
1 G
yz
(4-6)
z
1 E
[(1
) z
],
zx
1 G
zx
10
弹性与塑性 力学基础
第四章 广义胡克定律和弹性力学解题的 基本方程与方法