当前位置：文档之家 › 弹性与塑性力学基础-第4章广义虎克定律和弹性力学解题

弹性与塑性力学基础-第4章广义虎克定律和弹性力学解题

  • 格式：ppt
  • 大小：1.77 MB
  • 文档页数：44

下载文档原格式

  / 44

合集下载

6弹塑性4_弹性基本问题与解法_2012课件第一部分

6弹塑性4_弹性基本问题与解法_2012课件第一部分

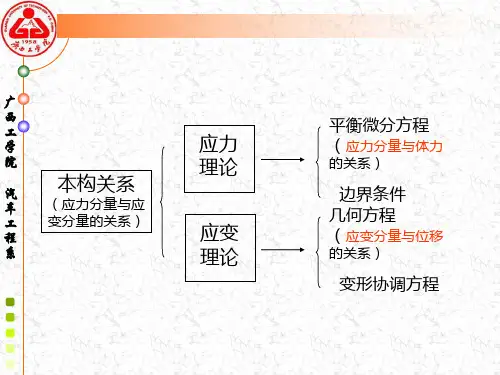
第四章一、线性弹性理论适定问题的基本方程和边界条件对于线弹性体小变形的线性问题，建立了一组线性方程组可以描述为在S 为边界的域V 上以u ,ε,σ作为求解变量的偏微分方程边值问题：微分提法2变分提法积分提法第四章第四章适定问题：第四章均匀变形状态()()1222111 1d d E c d d E c νν−=−=第四章弹性力学的基本方程和解法一、线性弹性理论适定问题的基本方程和边界条件 适定问题与非适定问题简例蓝色：边界给定量红色：边界未知量6适定问题例一第四章蓝色：边界给定量红色：边界未知量7适定问题例二第四章蓝色：边界给定量红色：边界未知量8适定问题例三边界全部给定面力时约束刚体位移才能求得确定位移边界全部给定面力时给定面力和体积力必须整体平衡第四章蓝色：边界给定量红色：边界未知量9非适定问题例一有多余边界条件情况一般无解第四章蓝色：边界给定量红色：边界未知量10非适定问题例二边界条件识别（逆问题）复杂！第四章 1.3 界面连续条件第四章弹性力学的基本方程和解法一、线性弹性理论适定问题的基本方程和边界条件II I u u =IIIi i u u =位移面力3个条件0t t =+II I 0II II I I =+ji j ji j n n σσIII S IIS +−u3个条件+12∀X ∈S It I I t0)(II I I =−ji ji j n σσ界面连续条件应为边界条件个数的两倍I S第四章第四章第四章第四章第四章第四章第四章第四章第四章第四章第四章。

弹塑性力学第四章答案

弹塑性力学第四章答案

第四章 习题答案4.3有一块宽为a ，高为b 的矩形薄板，其左边及下边受链杆支承，在右边及上边分别受均布压力1q 和2q 作用，见题图4.1，如不计体力，试求薄板的位移。

题图4-1解：1.设置位移函数为123123()()u x A A x A y v y B B x B y =+++⎫⎬=+++⎭（1）因为边界上没有不等于零的已知位移，所以式00,m m m m mmu u A u v v A v =+=+∑∑中的0u 、0v 都取为零，显然，不论式（1）中各系数取何值，它都满足左边及下边的位移边界条件，但不一定能满足应力边界条件，故只能采用瑞兹法求解。

2.计算形变势能。

为简便起见，只取1A 、1B 两个系数。

111111,u A x Au v B y B v ==== （2） 11,0,,0uuvu A B x yyx∂∂∂∂====∂∂∂∂ ()()2222111111112200222(1)2(1)a b E Eab U A B A B dxdy A B A B v v νν=++=++--⎰⎰ （3） 3.确定系数1A 和1B ，求出位移解答。

因为不计体力()0X Y ==，且注意到1m =，式4-14简化为11UXu ds A ∂=∂⎰ （4）11UYv ds B ∂=∂⎰ （5） 对式（4）右端积分时，在薄板的上下边和左边，不是0X =，就是10u =，故积分值为零。

在右边界上有11,,X q u x a ds dy =-===()111bXu ds q ady q ab =-=-⎰⎰ （6）同理，式（5）右端的积分只需在薄板的上边界进行，()1220aYv ds q bdx q ab =-=-⎰⎰ （7）将式（3）、式（6）、式（7）分别代入式（4）、式（5）可解出1A 和1B ：()1112222(1)EabA B q ab v ν+=---()1122222(1)EabB A q ab v ν+=--- 121q q A E ν-=-， 211q q B E ν-=- （8） 122111,q q q q u A x x v B y y E Eνν--==-==- （9）4．分析：把式(8)代入几何和物理方程可求出应力分量，不难验证这些应力分量可以满足平衡微分方程和应力边界条件，即式(8)所示位移为精确解答。

弹塑性力学简答题

弹塑性力学简答题

弹塑性力学简答题第一章 应力1、 什么是偏应力状态？什么是静水压力状态？举例说明？静水压力状态时指微六面体的每个面只有正应力作用，偏应力状态是从应力状态中扣除静水压力后剩下的部分。

2、应力边界条件所描述的物理本质是什么？物体边界点的平衡条件。

3、对照应力张量ij δ与偏应力张量ij S ，试问：两者之间的关系？两者主方向之间的关系？相同。

110220330S S S σσσσσσ=+=+=+。

4、为什么定义物体内部应力状态的时候要采取在一点的领域取极限的方法？不规则，内部受力不一样。

5、解释应力空间中为什么应力状态不能位于加载面之外？保证位移单值连续。

连续体的形变分量x ε、y ε、xy τ不是互相独立的，而是相关，否则导致位移不单值，不连续。

6、Pie 平面上的点所代表的应力状态有何特点？该平面上任意一点的所代表值的应力状态1+2+3=0，为偏应力状态，且该平面上任一法线所代表的应力状态其应力解不唯一。

固体力学解答必须满足的三个条件是什么？可否忽略其中一个？第二章 应变1、从数学和物理的不同角度，阐述相容方程的意义。

从数学角度看，由于几何方程是6个，而待求的位移分量是3个，方程数目多于未知函数的数目，求解出的位移不单值。

从物理角度看，物体各点可以想象成微小六面体，微单元体之间就会出现“裂缝”或者相互“嵌入”，即产生不连续。

2、两个材料不同、但几何形状、边界条件及体积力（且体积力为常数）等都完全相同的线弹性平面问题，它们的应力分布是否相同？为什么？相同。

应力分布受到平衡方程、变形协调方程及力边界条件，未涉及本构方程，与材料性质无关。

3、应力状态是否可以位于加载面外？为什么？不可以。

保证位移单值连续。

连续体的形变分量x ε、y ε、xy τ不是互相独立的，而是相关，否则导致位移不单值，不连续。

4、给定单值连续的位移函数，通过几何方程可求出应变分量，问这些应变分量是否满足变形协调方程？为什么？满足。

弹塑性力学第四章

弹塑性力学第四章

代入广义胡克定律
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
c11 x c12 y c13 z c14 xy c15 yz c16 zx
b
广义胡克定律
由应力分量的坐标变换公式（2-20）可得：
广 西 工 学 院 汽 车 工 程 系
xy l11l22 xy xy 2 x l11 x x 2 y l22 y y 2 z l33 z z
上述关系式是胡克（Hooke）定律在复杂应力条件下 的推广，因此又称作广义胡克定律。
广义胡克定律
广义胡克定律的张量表示： ij cijkl kl cijkl 称为弹性系数，一共有36个。
i, j, k , l 1, 2.3
广 西 工 学 院 汽 车 工 程 系
如果物体是非均匀材料构成的，物体内各点受力后将 有不同的弹性效应，因此一般的讲，cmn 是坐标x，y，z 的函数。 如果物体是由均匀材料构成的，那么物体内部各点， 如果受同样的应力，将有相同的应变；反之，物体内各 点如果有相同的应变，必承受同样的应力。 因此cmn为弹 性常数，与坐标无关。 各向同性材料，独立的弹性常数只有两个。
xy yz zx
xy
G
yz
G
zx
G
式中， G
E 2 1 v
为各向同性物体的剪切弹性模量。
表示材料弹性性能的常数有3个，但只有两个是独立的。 张量记法：
1 v v ij ij E E vE ij e E ij ij 1 v 1 v 1 2v

弹塑性力学第四章

弹塑性力学第四章

若通过物体每一点可作这
样的轴（如x3轴），在此轴 成垂直的平面内，所有射
线方向的弹性性质都是相
同的，称这个平面为各向
同性面，如地层属于此类。
[C]中独立系数为5个：
x1
x3 x2’
x2Fra bibliotek各向同性面
x1’
2019/10/18
28
§4-2 线弹性体的本构关系
2.4 横观各向同性材料——弹性体对一个轴对称
ij
2019/10/18
12
§4-1 应变能、应变能密度与弹性材料的
本构关系
W ijij
比较上面二式，得：
W

W
ij
ij
ij

W
ij

fij ( kl )——本构关系（方程）
适用于各种弹性情况（线性、非线性）
2019/10/18
13
§4-1 应变能、应变能密度与弹性材料的 本构关系
本构关系
时刻达到 应变增量
t
+t：位移有增量 u

ijeie j

uiei
外力功增量 ：


A V f udV SF udS
2019/10/18
8
§4-1 应变能、应变能密度与弹性材料的
本构关系


：函数增量

A V f udV SF udS
WdV
V
S Fi uidS S (ij ui )njdS V ( ji ui ), j dV
代入外力功增量
2019/10/18
10
§4-1 应变能、应变能密度与弹性材料的 本构关系

第四章广义胡克定律

第四章广义胡克定律

式中共有 36 个常数。
（三）弹性常数矩阵的对称性
上述 36 个常数并不都是独立的，从§4.3 节能量角度考虑，弹性常数矩阵是对称的，即极端
2
弹性力学讲义（2013 版），山东大学岩土中心 王者超
各向异性的弹性体其独立弹性常数只有 21 个。 根据材料本身性质的对称性，独立的弹性常数个数将发生变化。 若材料具有一个对称面，则弹性常数减少至 13 个； 若材料具有三个正交的对称面，即材料具有正交各向异性，则弹性常数减少至 9 个； 若材料是横观各向同性的，则弹性常数减少至 5 个； 最后，若材料是各向同性的，则弹性常数只有 2 个。
+
c24ε
′
12
+
c25ε
′
23
+
c26ε
′
31
⎪⎪σ ⎨
′
33
=
c31ε
′
11
+
c32ε
′
22
+
c33ε
′
33
+
c34ε
′
12
+
c35ε
′
23
+
c36ε
′
31
⎪σ ⎪
′
12
=
c41ε
′
11
+
c42ε
′
22
+
c43ε
′
33
+
c44ε12′
+
c45ε
′
23
+
c46ε
′
31
⎪σ ⎪
′
23
=
c51ε11′
1
弹性力学讲义（2013 版），山东大学岩土中心 王者超

弹塑性力学第四章

弹塑性力学第四章

y c21 x c22 y c23 z z c31 x c32 y c33 z
x 对 x 的影响应与 y 对 y 及 z 对 z 的影响相同，即 c11 c22 c33
y , z 对 x 的影响应相同，即 同理，
因而有：
c12 c13
c11 c22 c33 a c12 c21 c13 c31 c23 c23 b
对于应变主轴，弹性常数只有两个。
广义胡克定律
各向异性弹性体独立的常数有21个。 系数矩阵对称 Cmn Cnm 广 西 工 具有一个弹性对称面的各向异性弹性体的独立常数有13个。 学 院
广义胡克定律
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院 汽 车 工 程 系
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院
x 汽 x 车 工 2 2 2 x l11 y l12 z l13 2 xy l11l12 yz l12l13 xz l11l13 x x 程 系 ,
y y z z
z
y
y
z
ij liil jj ij
车 工 程 系
弹性对称面：如果物体内存在这样一个平面，和该平面对称的 汽 两个方向都具有相同的弹性，则该面称为物体的弹性对称面。 弹性主方向：垂直于弹性对称面的方向 具有三个弹性对称面的各向异性弹性体（正交各向异性）的 独立常数有9个。
广义胡克定律
证明：正交各向异性弹性体的独立常数有9个。 证明：取弹性主轴为三个坐标轴，将z轴旋转180度

弹塑性力学第04章

弹塑性力学第04章

x=rcosθ y=rsinθ z=z
图（4-1）
1．平衡微分方程



在轴对称情况下，由于方向的 对称性，切应力τ θ z=τ zθ =0， τ rθ =τ θ r=0； 应力分量σ r，σ θ ，σ z，τ zr， 均为r与z的函数； 体力分量只有沿r与z方向的Fr 与Fz； 则可得r与z方向的平衡微分方 程：
4.边界条件
（1）侧面边界上
dy l , ds
f x f y f z 0 外法线n的方向余弦为 dx m , n0 ds
将6个应力分量代入应力边界条件，前两式自然满足，而第三式为
dx dy d 0 x ds y ds ds
则积分后可得φ=K （在横截面周界c上） 其中，K为常数。对单连通区域（实心杆），可以取K=0，即
φ（x,y）=0 （在横截面周界c上） （4-18）
这是因为，由式（4-17）可知，当扭转应力函数φ相差一个常数K 时，对求应力分量无影响。
（2）端面边界条件（以上端面为例）
R zydxdy 0 R ( x zy y zx )dxdy M R
zr
r
2 2 2 2 z 2 2 1 2 z
（4-7）
能够满足式（4-6）的双调和函数列出如下：
五次幂 四次幂 三次幂 二次幂 一次幂 零次幂 负一次幂 负二次幂 负三次幂 r 2 z 3r 2 4 z 2 , z 3 5r 2 2z 2 2 2 2 2 2 2 r r 4z , z 3r 2z 2 3 3 r z, z , z ln r z 2 lnr R, zlnr,zlnR z -1 R z zR , ln R -1 zR -3 2 2 5 r 2z R

06-弹性力学解题方法

06-弹性力学解题方法

§4－3 按应力求解弹性力学问题
基本方程
ij
x j
fi
0
ij
1
E
ij
E
ij
ij
1 ui 2 x j
u j xi
相容方程（应变协调方程）：
2 x
y 2
2 y
x 2
2 xy
xy
2 y
z 2
2 z
y 2
2 yz
yz
2 z
x 2
2 x
z 2
2 zx
zx
x
xy
z
zx
弹性方程：
r
E
1
1
2
u r
1
E
1
2
u r
z
E
1
1
2
w z
zr
E 2(1
)
u z
w r
r z 0
z 0 r 0
E 2(1

)
1
1
2
r
2u
u r2
fr
0
u u w
E 2(1
)
1
1
2
z
2w
fz
0
r r z
2
2 r 2
1 r
r
2 z 2
u z
w x
Fx
lG
u y
v x
m
2G
v y
nG
v z
w y
Fy
解题思路：
G
1 2
xi
G 2ui
fi
0
（4－3）
n
jG
ui x j
u j xi

弹塑性力学第四章弹性力学的求解方法

弹塑性力学第四章弹性力学的求解方法

微分方程并求解，最后根据边界条件确定待定常数。
逆解法求解空间问题
逆解法的基本思想
从已知的空间应力或位移函数出发，反推得到弹性体的形状和边界条件。
适用于具有特定应力或位移分布的空间问题
如无限大体、半无限大体等具有特殊应力或位移分布的空间问题。
求解步骤
假设空间应力或位移函数，根据弹性力学基本方程推导得到弹性体的形状和边界条件，并 验证假设的合理性。
04
半解析法在弹性力学中的应用
有限差分法基本原理及步骤
差分原理
有限差分法基于差分原理，将连续问 题离散化，通过求解差分方程得到近 似解。
网格划分
将求解区域划分为规则的网格，每个 网格节点对应一个未知数。
差分格式
根据问题的性质和精度要求，选择合 适的差分格式，如向前差分、向后差 分、中心差分等。
边界处理
电测实验方法介绍及优缺点分析
电阻应变片法
利用电阻应变片将试件表面的应变转换 为电阻变化，通过测量电路获取应变信 息。该方法具有测量精度高、稳定性好 、适用于各种环境和试件形状的优点， 但需要粘贴应变片并进行温度补偿，且 只能进行点测量。
VS
电容传感器法
利用电容传感器将试件表面的位移或应变 转换为电容变化，通过测量电路获取相关 信息。电容传感器法具有非接触、高灵敏 度、宽频响等优点，但易受环境干扰，且 需要进行复杂的电路设计和信号处理。
04 边界条件处理 根据边界条件对总体刚度矩阵和荷载向量进行修正。
05
求解线性方程组
求解总体刚度矩阵和荷载向量构成的线性方程组，得 到节点位移。
边界元法基本原理及步骤
边界积分方程
边界离散化
单元分析
总体合成
求解线性方程组

清华大学研究生弹塑性力学讲义 5弹塑性_弹性力学的基本方程与解法

清华大学研究生弹塑性力学讲义 5弹塑性_弹性力学的基本方程与解法

弹塑性力学第四章 弹性力学的基本方程与解法一、线性弹性理论适定问题的基本方程和边界条件对于在空间占有体积域V 的线弹性体在外加恒定载荷和固定几何约束条件下引起的小变形问题，若以, ,u εσ作为求解变量，则可以建立如下偏微分方程边值问题： 几何方程()1,,2ij i j j i u u ε=+ ()12∇+∇u u ε= (1a)广义胡克定律 ij ijkl kl E σε= :E σ=ε(1b)平衡方程 ,0ij j i f σ+= ∇⋅+=f 0σ V∀∈x (1c)以上方程均要求在域内各点均满足。

边界条件 u u i i = ∀∈x S ui (2a)n t j ji i σ= ∀∈x S ti(2b)对于适定问题，即不仅要求保证解存在唯一，而且有较好的稳定性。

当载荷或边界条件给定值有微小摄动时，应能保证问题解的变化也是微小的。

对于边界条件的提法就有严格的要求。

即要求：S S S S S ui ti ui ti U I ==∅(2c)对于各向同性材料，其广义胡克定律可具体写成 σλεδεij kk ij ij G =+2 ()tr 2G λ+I σ=εε (3a)()11ij ij kk ij E ενσνσδ⎡⎤=+−⎣⎦ ()()1tr Eνν=⎡⎤⎣⎦I ε1+σ−σ (3b)以上就域内方程来说，一共是对于u ,,σ ε的15个独立分量u i ij ij ,, σε的15个方程。

对于边界条件来说，三维问题每点有三个边界条件，而且是在三个正交方向上每个方向有一个边界条件，这个边界条件或者给定位移、或者给定面力。

这三个正交第四章 弹性力学的基本方程与解法方向可以是整体笛卡儿坐标系的三个方向，也可以是边界自然坐标系的三个方向（即法向和两个切向）。

从更一般来说，除去给定位移或面力外，还有另一种线性的边界条件t K u c i ij j i +=(4)这是一种弹性约束条件。

用这个条件可以取代给定位移或给定面力的条件。

清华大学研究生弹塑性力学讲义 4弹塑性_弹性材料的广义胡克定律

清华大学研究生弹塑性力学讲义 4弹塑性_弹性材料的广义胡克定律

具有单值关系的弹性范围内，σ ∼ ε ′ 也同样具有单值关系，而且当σ ∼ ε 具有线性关系
的线弹性范围内，σ ∼ ε ′ 也同样具有线性关系。也就是说，上述比例极限、弹性极限都
是针对整个均匀变形状态的，而不是针对变形状态的某个应力、应变分量的。试验还
表明，在线弹性范围内横向收缩应变与轴向伸长应变之比是一个常数，即
3. 由于线弹性材料的应力张量与应变张量之间满足线性关系，因此应变能密度函数不 仅可以用应变分量来表示，还可以用应力分量来表示，试导出各向同性弹性材料用 应力分量表示应变能密度函数的公式。
4. 对于线弹性材料，试证明如下卡氏公式：
∂W ∂σ ij
= εij
5. 将应力张量和应变张量分别分解为球形张量和偏斜张量之和，即
⎪⎪σ
22
⎪ ⎪
⎢ ⎢
E E 2222
2233
0
0
0
⎥⎪ ⎥⎪
ε 22
⎪ ⎪
⎪⎪σ ⎨⎪σ
33 23
⎪⎪ ⎬ ⎪
=
⎢ ⎢ ⎢
E3333
0
0
E2323
0
0 0
⎥ ⎥ ⎥
⎪⎪⎨⎪2εε3233
⎪⎪ ⎬ ⎪
(14)
⎪σ ⎪⎪⎩σ
31 12
⎪ ⎪ ⎪⎭
⎢ ⎢ ⎣⎢
sym.
E3131
0 E1212
⎥ ⎥ ⎦⎥
E
2(1 +ν
)
⎛ν ⎜⎝ 1 − 2ν
ε iiε
jj
+
ε ijε ij
⎞⎤ ⎟⎠⎥⎦
(18)
独立常数
E= ν= λ= μ =G = K=
表 1 各向同性弹性体弹性常数间的关系

弹塑性力学-04

弹塑性力学-04

x E y
其中E为弹性常数，这就是熟知的 胡克定律。
在三维应力状态下，描绘一点处的 应力状态需要9个应力分量，与之 相应的应变状态也要用9个应力分 量来表示。在线弹性阶段，应力与 应变间仍有线性关系存在，但在一 般情况下，任一应变分量要受9个 应力分量 制约。
3
由于应力张量与应变张量的对称性
10
x e 2 x , xy xy
y e 2 y , yz yz z e 2 z , zx zx
x x ( y z ) (3 2 ) 2 (3 2 )
正交各向异性的弹性材料的本构关系，可根据任一坐标轴 反转时弹性常数保持不变的要求
c12 x c22 y c23 z c11 , c22 , c33 , c12 , c13 , c23 , c44 , c55 , c66 c13 x c23 y c33 z c44 xy 共9个弹性常数 c55 yz c66 zx
1 x ( x v y ) E 1 y ( y v z ) E v z ( x y ) E 1 xy xy G
如用应变分量表示应力分量
14
对于平面应变问题
z yz zx 0
E x [(1 v) x v y ] (1 v)(1 2v) E y [v x (1 v) y ] (1 v)(1 2v) vE z ( x y ) (1 v)(1 2v) xy G xy
c 41 x c 42 y c 43 z c 44 xy c 45 yz c 46 zx c51 x c52 y c53 z c54 xy c55 yz c56 zx c61 x c62 y c63 z c64 xy c65 yz c66 zx

弹塑性力学第4章

弹塑性力学第4章
3
B 0,0,0
A 1 , 2 , 3
1
2
B点坐标原点，平均应力=0的应力状态
4.2.2屈服曲面：
f 上述屈服条件在应力空间所表达的曲面称之为屈服曲面。
1
, 2 , 3 C
f 1 , 2 , 3 C f 1 , 2 , 3 C
1 2k s , k s
2
Tresca 屈服条件可以表示为：

2 3 s 3 1 s 1 2 s
复杂应力状态下判断物体是否进入塑性阶段的公式。
Tresca 屈服条件的优缺点： 优点：当主应力顺序已知时，表达式简单 缺点： 1）当主应力顺序未知时，表达式复杂 2) 只考虑最大最小主应力 3) 屈服曲面为正六角柱面，棱边处切平面不唯一
Mises 屈服条件 用下列方程表示： 1 2 或
2
2 3 3 1 6B 2
2 2
2

x y

2
y z

2
2 2 2 6B 2 z x +6 xy yz zx


即：
f ij 0
加载过程 卸载过程
点在屈面上移动为加载过程
加载准则
f 0
f 0
f 0
理想材料 强化材料 加载
加载 中性变载
卸载 卸载
屈服条件为Mises的加载准则
J 2 0/ i 0
J 2 0/ i 0
J 2 0/ i 0
2s
3
Mises屈服条件的表达式：
x y y z z x +6 xy 2 yz 2 zx 2 2 s 2

弹性与塑性力学总结

弹性与塑性力学总结

4.2弹性力学问题可分为三类 第一类问题：宜用应力解法 第二类问题：宜用位移解法： 第三类问题：宜用混合解法
4.3拉梅方程（位移表示的平衡方程）
(λ +G)θ, j +G 2ui + fi = 0 ∇
4.4密歇尔、贝尔特拉密方程（应力协调方程）
1 1+ µ ∇ σij + Θ,ij =− [µδij fkk −(1− µ2 )( fi, j +) f j,i ] 1+ µ 1− µ
1.3应力张量
σx τxy τxz σij = τ yx σy τ yz τzx τzy σz σx −σm τxy τxz σm 0 0 = τ yx σy −σm τ yz + 0 σm 0 τzx τzy σz −σm 0 0 σm Sx Sxy Sxz σm 0 0 = Syx Sy Syz + 0 σm 0 Szx Szy Sz 0 0 σm = Sij +σmδij
弹性力学总结 1 应力理论 2 应变理论 3弹性应力应变关系 4弹性理论的解题方法 5弹性力学平面问题
1 应力理论 1.1应力矢量的定义
1.2一点应力状态的描述 应力张量完全确定了一点的应力状态
σx τxy τxz σij = τ yx σy τ yz =σmδij + Sij τzx τzy σz
' 2
S1 =σ1 −σm S2 =σ2 −σm S3 =σ3 −σm
1.7三类边界条件
•应力边界条件
px =σx l + τxy m +τxz n py = τyx l + σy m +τyz n

弹塑性力学定理和公式

弹塑性力学定理和公式

弹塑性⼒学定理和公式应⼒应变关系弹性模量||⼴义虎克定律1.弹性模量对于应⼒分量与应变分量成线性关系的各向同性弹性体,常⽤的弹性常数包括:a弹性模量单向拉伸或压缩时正应⼒与线应变之⽐,即b切变模量切应⼒与相应的切应变之⽐,即c体积弹性模量三向平均应⼒与体积应变θ(=εx+εy+εz)之⽐,即d泊松⽐单向正应⼒引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之⽐,即此外还有拉梅常数λ。

对于各向同性材料，这五个常数中只有两个是独⽴的。

常⽤弹性常数之间的关系见表3-1 弹性常数间的关系。

室温下弹性常数的典型值见表3-2 弹性常数的典型值。

2.⼴义虎克定律线弹性材料在复杂应⼒状态下的应⼒应变关系称为⼴义虎克定律。

它是由实验确定，通常称为物性⽅程，反映弹性体变形的物理本质。

A各向同性材料的⼴义虎克定律表达式（见表3-3 ⼴义胡克定律表达式）对于圆柱坐标和球坐标，表中三向应⼒公式中的x 、y、z分别⽤r、θ、z和r、θ、φ代替。

对于平⾯极坐标，表中平⾯应⼒和平⾯应变公式中的x、y、z⽤r、θ、z代替。

B⽤偏量形式和体积弹性定律表⽰的⼴义虎克定律应⼒和应变量分解为球量和偏量两部分时，虎克定律可写成更简单的形式，即体积弹性定律应⼒偏量与应变偏量关系式在直⾓坐标中，i,j=x,y,z；在圆柱坐标中，i,j=r,θ,z,在球坐标中i,j=r,θ,φ。

弹性⼒学基本⽅程及其解法弹性⼒学基本⽅程|| 边界条件|| 按位移求解的弹性⼒学基本⽅法|| 按应⼒求解的弹性⼒学基本⽅程|| 平⾯问题的基本⽅程|| 基本⽅程的解法|| ⼆维和三维问题常⽤的应⼒、位移公式1.弹性⼒学基本⽅程在弹性⼒学⼀般问题中，需要确定15个未知量，即6个应⼒分量，6个应变分量和3个位移分量。

这15个未知量可由15个线性⽅程确定，即(1)3个平衡⽅程[式（2-1-22）]，或⽤脚标形式简写为(2)6个变形⼏何⽅程[式（2-1-29）]，或简写为(3)6个物性⽅程[式（3-5）或式（3-6）]，简写为或2.边界条件弹性⼒学⼀般问题的解，在物体部满⾜上述线性⽅程组，在边界上必须满⾜给定的边界条件。

工程弹塑性力学第四章弹性理论的解题方法.ppt

工程弹塑性力学第四章弹性理论的解题方法.ppt
（1）叠加原理
设线弹性体体积为V，表面为S，如果两组外力（体 力和面力）同时作用在物体上所产生的效果（应力、应 变和位移）等于它们分别作用所产生的效果之和。
由于线弹性力学的求解方程（15个）均为线性微分 （代数）方程，很容易证明这个原理成立。 对于非线性问题，此原理不能。
线弹性力学的几个原理
（2）解的唯一性定理
上述位移法、应力法和混合法统称为直接解法。 尽管这些方法的建立在理论上有着重大意义，但在实 际解题过程中却很少原原本本地按上述步骤去做，原 因还是在于数学上的困难和复杂性。在弹塑性力学解 题方法中经常采用如下方法：
（1）逆解法：设位移或应力的函数式是已知的，
然后代入上述有关方程中求得应变和应力或应变和位
考虑用位移表示的平衡方程式（4-9）拉梅方程，在不 考虑惯性力项时有：
( G),i G2ui fi 0
对式（a）求导一次，有：
( G),ii G2ui,i 0
（a）
( 2G)2 0
2 0
即体应变满足拉普拉斯方程，为调和函数。
J4U.4ST常体江积苏力科下技应大力学和位Jia移ngsu的Univ特ersit点y of Science and Technology
（4）物理方程 （本构方程）
各向异性材料：
ij Cijkl kl
Cijkl Cklij C jikl Cijlk
各向同性材料：
ij 2G ij ij
ii 11 22 33
或者
ij

1 2G


ij

3

2G
J1 ij
注意事项：
(1) 必须满足静力等效条件；

弹性力学第4章—弹性本构关系

弹性力学第4章—弹性本构关系
将上式代入各向同性材料的广义胡克定律，得到
τ yz ⎫ 1 ε x = [σ x − ν (σ y + σ z )], γ yz = ⎪ E G ⎪ τ ⎪ 1 ε y = [σ y − ν (σ x + σ z )], γ xz = xz ⎬ E G⎪ τ xy ⎪ 1 ε z = [σ z − ν (σ x + σ y )], γ xy = ⎪ E G⎭
用张量形式表示为
1 ε ij = [(1 +ν )σ ij −νσ kkδ ij ] E
vEδ ij ε kk E σ ij = ε ij + (1 + v )(1 − 2v ) 1+ v
反之也可以用应变表示应力
第四章结束
ε x' = ε x ,ε y' = ε z ,ε z' = ε y ⎫ γ y ' z ' = −γ yz , γ x ' z ' = −γ xy , γ x ' y ' = γ xz ⎬ ⎭
将它们代入横观各向同性弹性体的广义胡克定律，得到
1 C12 = C13 , C11 = C33 , C55 = (C11 − C12 ) 2 σ x = λθ + 2 με x τ xy = μγ xy ⎫ 所以弹性常数从5个减少到2个 ⎪ σ y = λθ + 2 με y τ yz = μγ yz ⎬ σ z = λθ + 2 με z τ xz = μγ xz ⎪ ⎭
将它们代入正交各向异性弹性体的广义胡克定律，得到
C11 = C22
C13 = C23
C55 = C66
所以弹性常数从9个减少到6个
4.1 广义胡克定律
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

σx
E
−µ
σx
E
的作用： 由于应力σy的作用： y方向应变为 方向应变为 x方向应变为 方向应变为
σy
E
作用在x方向及 方向的应变为 方向及y方向 同时有σx和σy作用在 方向及 方向的应变为
−µ
σy
E
1 εx = −µ = (σ x − µσ y ) (4-3) E E E σy σ 1 εy = − µ x = (σ y − µσ x ) E E E
ε0 =
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4ቤተ መጻሕፍቲ ባይዱ1 广义虎克定律
4.1.4 广义虎克定律的不同形式 引入以上表达式后，广义虎克定律又可写为： 引入以上表达式后，广义虎克定律又可写为：
1 1 ε x = [(1 + µ )σ x − µΘ], γ xy = τ xy E G 1 1 ε y = [(1 + µ )σ y − µΘ], γ yz = τ yz E G 1 1 ε z = [(1 + µ )σ z − µΘ], γ zx = τ zx E G
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
4.1.4 广义虎克定律的不同形式
1 ex = σ′ = σ′ x x E 2G 1+ µ 1 ′ = ey = σy σ′ y E 2G 1+ µ 1 ez = σ′ = σ′ z z E 2G
1 ε x = [σ x + µσ x − µ (σ x + σ y + σ z )] E 即得式(4-6)的第一式 ε = 1 [(1 + µ )σ − µΘ] 即得式 的第一式 x x E 1 − 2µ 利用式(4-5) 利用式 θ= Θ
E
便可得 由上式可得
1 E ε x = [(1 + µ )σ x − µ θ] (1 − 2 µ ) E E µE σx = εx + θ 1+ µ (1 + µ )(1 − 2 µ )
3、平面应力状态: 平面应力状态: 对于各向同性的均匀材料，根据实验结果，在小变形的情况下， 对于各向同性的均匀材料，根据实验结果，在小变形的情况下， 正应力和剪应变没有关系，而剪应力只与剪应变有关， 正应力和剪应变没有关系，而剪应力只与剪应变有关，且应力的 叠加原理是适用的 是适用的。 叠加原理是适用的。
（各向同性均匀材料的 含义， 含义，即材料内部各处 的不同方向具有相同的 μ、E、G 值）
1 ε x = [σ x − µ (σ y + σ z )] E 1 ε y = [σ y − µ (σ x + σ z )] E 1 ε z = [σ z − µ (σ x + σ y )] E τ xy γ xy = G τ yz γ yz = G τ zx γ zx = G
(4-4)
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
4.1.4 广义虎克定律的不同形式 将式(4-4)的前三式左右两边相加后，则有 的前三式左右两边相加后， 将式 的前三式左右两边相加后
εx +εy +εz =
σx
σy
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
3、平面应力状态： 平面应力状态： 作用下， 方向的应变 在σx和σy作用下，z方向的应变
εz= -µ(σx＋σy)/E
在剪应力作用下， X-Y 平面内的剪 平面内的剪 在剪应力作用下， 应变与纯剪时相同， 应变与纯剪时相同，即：
即：
1 σ′ = σ′ ex = x x 2G E
1+ µ
式中： 为应变偏量分量， x 为应力偏量分量。 式中： ex=εx- ε0 为应变偏量分量，σ ′ = σ x − σ m 为应力偏量分量。 用相同的方法，可得： 用相同的方法，可得：
ey =
1+ µ 1 σ′ = σ′ y y E 2G
1+ µ 1 ′ = ez = σz σ′ z E 2G
平面双向拉（ 平面双向拉（压）应力
纯剪应力状态
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院 平 面 应 力 时 的 虎 克 定 律
§4-1 广义虎克定律
3、平面应力状态: 平面应力状态: 的作用： 由于应力σx的作用： x方向应变为 方向应变为 y方向应变为 方向应变为
εy = εz =-μ·εx
式中： 式中： Ε－弹性模量， μ－泊松比
τxy=
G · γxy
G 式中： －剪切模量， 式中：G－剪切模量， =
E 2 (1 + µ )
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
(4-6)
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
4.1.4 广义虎克定律的不同形式 由式(4-6)及式 及式(4-5)，可得 由式 及式 ，
ε x − ε0 =
1 1 − 2µ [(1 + µ )σ x − µΘ] − σm E E 1 1 − 2µ = [(1 + µ )σ x − 3µσ m ] − σm E E 1+ µ = (σ x − σ m ) E
因此，弹性阶段应力莫尔圆和应变莫尔圆是成比例的，因为： 因此，弹性阶段应力莫尔圆和应变莫尔圆是成比例的，因为：
1+ µ
ey γ xy γ yz ex γ zx ez 1 = = = = = = σ ′ σ ′ σ ′ 2τ xy 2τ yz 2τ zx 2G x y z
(4-7)
弹性阶段应力主轴和应变主轴重合（注意： 弹性阶段应力主轴和应变主轴重合（注意：应力或应变球张量对 应力主轴或应变主轴无影响） 应力主轴或应变主轴无影响）
1 [(σ x + σ y + σ z ) − 2 µ (σ x + σ y + σ z )] E 1 − 2µ = (σ x + σ y + σ z ) E
1 − 2µ Θ E
如令
εx + ε y + ε z = θ = 3ε0 ,σ x +σ y +σ z = Θ= 3σm
θ=
则上式可写为
1 − 2µ σm (4-5) 或 E (4-5)表明：弹性变形时，体积变化与三个正应力之和即应力张量的 表明： 表明 弹性变形时， 球张量成正比，而与应力偏量无关。 球张量成正比，而与应力偏量无关。
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
4.1.1 问题的提出 弹性力学问题中，物体的受力与变形情况，需用15个变量来 弹性力学问题中，物体的受力与变形情况，需用15个变量来 15 描述。 个应力分量， 个位移分量， 个应变分量。 描述。即：6个应力分量，3个位移分量，6个应变分量。 已学的基本方程－ 已学的基本方程－9个。包括：变形体的平衡微分方程（微元 包括：变形体的平衡微分方程（ 体的力平衡） 几何方程（应变－位移关系） 体的力平衡）3个，几何方程（应变－位移关系）6个。 未知变量的个数（15）多于方程数（ 未知变量的个数（15）多于方程数（9）→必须研究受力物体 的应力与应变之间的关系→物理方程。对于弹性问题，即广义 的应力与应变之间的关系→物理方程。对于弹性问题， 虎克定律。 虎克定律。
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
4.1.3 广义虎克定律的不同形式 µE E 如引用λ 如引用λ= 并注意到 2G = 则有 (1 + µ )(1 − 2 µ ) 1+ µ
σ x = λθ + 2Gε x
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-1 广义虎克定律
4.1.3 广义虎克定律的不同形式 各向同性体的虎克定律(4-4)是以应力表示应变，在求解某些问题 是以应力表示应变， 各向同性体的虎克定律 是以应力表示应变 应变表示应力关系 时，有时需要用应变表示应力关系。将式 有时需要用应变表示应力关系。将式(4-4)第一式作如下改变 第一式作如下改变
(4-9)
E 3(1 − 2 µ )
则式(4-9)可写成 可写成(K—体积弹性模量 体积弹性模量) 则式 可写成 体积弹性模量
Θ = 3Kθ
(4-9')
弹性与塑性 力 学 基 础
第四章 广义虎克定律和弹性力学解题 的基本方程与方法
哈工大（威海） 哈工大（威海） 材料学院
§4-2 基本方程
4.2.1 弹性阶段本构关系 在弹性问题中，本构关系即广义虎克定律（ 个方程） 在弹性问题中，本构关系即广义虎克定律（6个方程） 4.2.2 平衡方程（3个方程） 平衡方程（ 个方程）
§4-2 基本方程
4.2.1 弹性阶段本构关系 4.2.3 几何方程 4.2.2 平衡方程 4.2.4 本构方程