2015年清华大学自主招生暨领军计划试题

清华大学历年自主招生试题汇总以下是2014年清华“领军计划”部分面试题：1、怎么看待单独二孩政策？2、谈谈对节假日安排的看法，有什么建议？3、怎么看待社会公平？以下是2014年清华“自强计划”部分面试题：结构性参考题目：提问：在你的同龄人中，当有些同学在为上学、吃饭、治病乃至整个家庭的生计发愁时，另外一些同学则在享受美味的食品、穿着流行的服装、接受各种优质的教育培训。

你如何看待这一现象?你是否认为这是一种社会不公?追问：你心目中的社会公平是怎样的?是否能够实现?若能实现，简要阐述实现的方法;若不能实现，请说说为什么?自由提问参考题目：请讲一个你的经历中体现你“自强”的故事。

你对自己的大学生活有何规划?将来想从事何种职业?你认为自己的家乡至今仍然贫困的原因是有哪些?应该如何解决?你曾经遇到过的最大困难是什么?你是如何面对和解决的?考察点：主要考察学生的个人理想与社会理想，是否能够独立思考并勇于创新，是否能够采取积极的方式克服困难与挫折;是否能够保持积极向上的心态等。

以下是清华大学2013年自主招生复试考题：1.近期上海、南京、杭州等地连续出现“H7N9禽流感”感染病例引起关注，公众非常想知道这方面的相关信息。

假如你是一位新闻发言人，你认为公众需要什么样的信息?追问:假如你发布信息后，社会出现恐慌，那该怎么办?2.“人类一思考，上帝就发笑”。

请就人类社会发展与大自然的关系发表评论。

追问:基于你的评价，你打算在当下和未来做些什么?3.请以“我和诺贝尔奖的距离”为题发表一段2分钟的演讲，可准备1分钟。

4.除了当选的10位人物外，举出你认为应该入围“2013‘感动中国’的一位人物”，并阐述理由。

2008年清华大学自主招生考试题目选语文（此文与原考试选用的文章稍有出入）（语文试题应该算是完整版了）：关于文学和它的寄主的故事朱大可关于文学死亡的话题，已经成为众人激烈争论的焦点。

这场遍及全球的争论，映射了文学所面临的生存危机。

一、选择题1.设复数z=cos 23π+isin 23π，则2111-1z z +-=（ ） (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列，p,q,k,l 为正整数，则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点，O 是坐标原点，若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1)，且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x yf xy++，x 、y ∈(-1,1)，则()f x 为(A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)−kx 有（ ）(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c ．若c=2，∠C=3π，且sinC+sin(B −A)−2sin2A=0,则有（ ）(A)b=2a (B)△ABC 的周长为△ABC 的面积为3(D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-，则（ ）(A)()f x 有极小值，但无最小值 (B) ()f x 有极大值，但无最大值 (C)若方程()f x =b 恰有一个实根，则b>36e (D)若方程()f x =b 恰有三个不同实根，则0<b<36e 8.已知A={(x,y)∣222x y r +=}，B={(x,y)∣222()()x a y b r -+-=，已知A∩B={(11,x y ),(22,x y )}，则（ ）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ，12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3，则5x+4y+3z 的最小值为（ ） (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ，若对任意正整数n ，总存在正整数m ，使得n S =m a ，则（ ）（A ）{n a }可能为等差数列 （B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ，总存在正整数m ，使得n a =m S11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（ ） (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中，AB=2，AD=A 1A =1，则A 到平面1A BD 的距离为（ ）(A)13 (B)23 (C)2(D)313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ，其面积为S ，则（ ）(A)若S=4，则k 的值唯一 (B)若S=12，则k 的值有2个(C)若D 为三角形，则0<k ≤23(D)若D 为五边形，则k>4 14.△ABC 的三边长是2,3,4，其外心为O ，则O A A B O B B C O C C A ⋅+⋅+⋅=（ ）(A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立，且P(B)=0.5，P(A −B)=0.2，则（ ）(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分，则这两部分的面积之比的（ ） (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形，则不同的选法有（ ）(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ，使得圆周222x y r +=上恰好有n 个整点，则n 可以等于（ ） (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|，则（ ） (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数，a =(mcos α,msin α)，b =(ncos β,nsin β)，其中α,β∈[0,2π)α,β∈[0,2π)．定义向量12a =(2α2α),12b 2β2β)，记θ=α−β，则（ ）(A)12a ·12a =a (B)1122a b ⋅=2θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足：1a =6，13n n n a a n++=，则（ ） (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中，下列方程表示的图形是椭圆的有（ ） （A ）ρ=1cos sin θθ+ （B ）ρ=12sin θ+ （C ）ρ=12cos θ- （D ）ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+，则（ ）（A ）()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ，若△ABC 为锐角三角形，则（ ） (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1)，若(0)f =(0)f '=1，则存在实数δ∈(0,1)，使得（ ） (A)()f x >0，x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1，x ∈(0,δ) (D)()f x >1，x ∈(−δ,0)26.在直角坐标系中，已知A(−1,0)，B(1,0)．若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n)，总存在两个不同的点i P ,j P ，使得|sin ∠A i P B −sin ∠A j P B|≤13，则n 的最小值为（ ）(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1，则的（ ）(A)最小值为45 (B)最小值为25 (C)最大值为1 (D)最大值为13+ 28.对于50个黑球和49个白球的任意排列（从左到右排成一行），则（ ）(A)存在一个黑球，它右侧的白球和黑球一样多 (B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（ ） (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0，则（ ） (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z+-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )662i i ππ+-=1，选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ，与公差d 的符号有关，选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅=2，正确；答案(B),|OA|+|OB|≥2≥2,正确；答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程，错误；答案(D)，原点到直线AB ：(111x x -)x-y+1=0的距离≤1，正确。

2021 北大自主招生题一1.整数 x,y,z 满足xy+yz+zx=1 ，那么(1+ 2 x )(1+2 y )(1+ 2 z)可A ． 16900B ．17900C ．18900D ．前三个答案都不对 2.在99 的正整出 50 个不同的正整50 个数中任两个的和都不等于 99，也不等于 1050 个数的和可能等于〔 〕A ． 3524B ．3624C ．3724D ．前三个答案都不对 3.x ∈[0, 2 数 a ，函数 y= g( a )的最大值为〔 〕 A ． 1 B ．2 C ．3 D ．前三个答案都不对 4. 20 10 - 20 n的整2 是 2 A ． 21 B ．22 C ．23 D ．前三个答案都不对 5.在形那A ． 6.9 B ．7.1 C ．7.3 D ．前三个答案都不对二 .填空题11x 12021足等式〔1+ ) (1 ) 的整数 x 的个数是 _______ ． x 2021( a b cd) 7. a,b,c,d ∈ [2,4] ，那么2 2 22(a d )(b c )的与___________8.对于任意实数 x ∈[1,5],|2x +px+q| ≤ 2,不超过22pq 的最大整数是 __________9.设x = 222bc a2bc,y= 222acb2ac,z= 2 22b ac2ba202120212021xyz的值为___,且 x+y+z=1 ，那么10.设A 1 ,A 2,..., A n 都是 9 元集合 {1,2,3, ⋯ ,9} 的子集， | A i |为奇数， 1≤ i ≤ n,| A i A j |为偶数， 1≤ i ≠j≤ n n 三．解答题11.数列 { a }为正项等比数列，且 a 3 a 4 a 1 a 2 =5,求naa 的最小值5612.f(x)为二次函数，且a,f(a),f (f(a)), f(f (f(a)))成正项等比数列，求证：f( a)= a13.称点都在三上的正此三角形的内接正方形。

2015年各高校自主招生考试试题回忆录一、北京大学今年北大自招太过亲民，遇到这样的自招题你敢想？一句周杰伦《青花瓷》里的歌词，问描述的是什么？答案有“青花瓷”、“青花盆”和“青花瓶”，你觉得选什么呢……北大语文试题只有一道题目，要求根据孟子《生于忧患死于安乐》和庄子《人间世》这两个材料，写一篇文章。

英语有阅读材料涉及美国白人警察枪杀黑人、贵州省一教育基金会受“郭美美事件”影响遭遇零捐助等时事热点。

面试部分考题：1.用一条长度一定的的绳子围成一个n边形，怎样围才能使围出的的n边形面积最大？2.后轮驱动的车辆，起动和刹车时，分别是车头翘起还是车尾翘起？判断并说明理由。

3.如何看待微信在人际交往中的作用？4.如何看待欧洲历史上的分与合？5.北京和张家口联合申办冬奥会面临哪些机遇和挑战？6.请用三个词概括中国传统文化，并谈谈中国文化如何真正“走出去”。

7.怎么看待追求财富导致雾霾的说法8.请谈一下动物迁徙的意义？9.谈谈你对嘀嘀打车与专车经营的看法。

10.你认为的文学阅读的最高境界是什么？11.请谈有教无类与因材施教的关系。

12.请谈你对国企高管限薪令的看法。

13.有人提议将网络战归为武力冲突，谈谈你的看法。

14.谈谈你对亚投行的看法。

15.有人提议在基础教育阶段实施男女分开管理，即开办男校和女校，谈谈你的看法。

16.谈一谈信仰、义务、责任的关系。

17.爱因斯坦说：“简单是科学追求的伟大目标。

”谈谈你的看法。

18.请你设计一下中国的养老体系？19.你如何看待就医不要钱这种理想设计？20.谈一谈你对批判性思维和惯性思维的关系的理解。

21.谈一谈你所认识的经济全球化下中国的粮食问题。

22.谈一谈自我意识？23.有人说在全球化背景下我国粮食安全已经不是一个问题，你怎么看？24.你对“绿水金山就是真金白银”有何看法？25.你对“贫富分化是经济发展必然现象”有何看法？26.谈一谈你对自主招生的看法。

二、2015年北京大学自主招生“博雅人才培养计划”部分面试题1.北京申办冬奥会有哪些机遇和挑战2.如何治理雾霾，有何建议3.中国传统文化将如何走出去4.微信在人际交往中的作用5.欧洲历史上的分与合6.如何看待中国申请冬奥会面试分为两个阶段，第二阶段为一对一考察理科生需在45分钟内，尝试解答一道物理题和一道数学题，然后分别接受一名物理考官和一名数学考官的一对一考察。

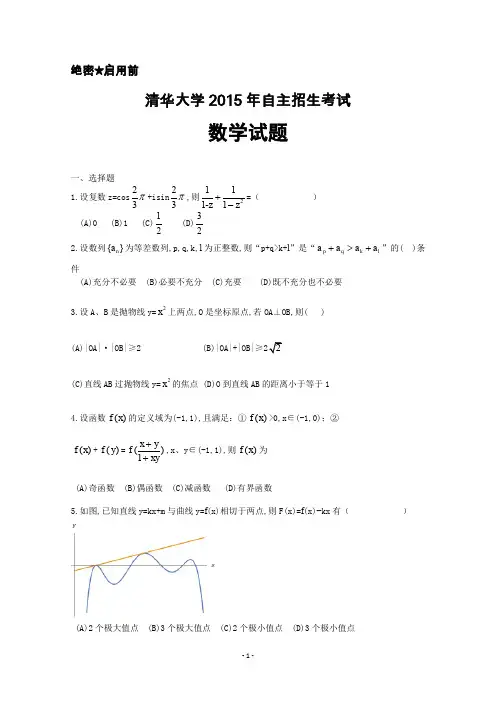
绝密★启用前清华大学2015年自主招生考试数学试题一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=（ ） (A)0 (B)1 (C)12 (D)32 2.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于1 4.设函数()f x 的定义域为(-1,1),且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x y f xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有（ ）(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点6.△ABC 的三边分别为a 、b 、c ．若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有（ ）(A)b=2a (B)△ABC 的周长为 (C)△ABC (D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-,则（ ）(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值(C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则（ ）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-=(C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为（ ）(A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n,总存在正整数m,使得n S =m a ,则（ ）（A ）{n a }可能为等差数列 （B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n,总存在正整数m,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是（ ）(A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为（ ）。

2016年清华大学领军计划测试题（数学+物理）特别说明：1、2016年清华领军计划测试为机考，全卷共100分。

2、考试时间：数学+物理共180分钟。

3、所有考题为不定项选择题。

以下内容为回忆版本，部分题改编成填空题。

4、物理测试共35题，回忆版中共26题，供大家参考。

A 、 数学部分1、已知椭圆22221(0)x y a b a b+=>>，两条直线1211:,:22l y x l y x ==-，过椭圆上一点P 作两条直线12,l l 的平行线，又分别交两条直线于,M N 两点，若||MN 为定值，则ab= （ ）A 、2 D 、42、已知,,x y z 为正整数，x y z ≤≤，那么方程11112x y z ++=的解的组数为 ( ) A 、8 B 、10 C 、11 D 、123、将16个数：4个1、4个2、4个3、4个4填入一个44⨯的矩阵中，要求每行、每列正好有2个偶数，则共有___________种填法。

4、已知O 为ABC ∆内一点，且满足::4:3:2AOB AOC BOC S S S ∆∆∆=，AO AB AC λμ=+， 则λ=___________，μ=_________。

5、“sin sin sin cos cos cos A B C A B C ++>++”是“ABC ∆为锐角三角形”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件6、各项均不相同的数列{}n a 中，1i i k N ≤<<≤，,,i j j k k i a a a a a a +++至少有一项在{}n a 中，N 的最大值为 （ ）A 、6B 、7C 、8D 、97、已知实数,,x y z 满足22211x y z x y z ++=⎧⎨++=⎩，则 （ ） A.max ()0xyz = B.min 4()27xyz =- C.min 23z =- D.以上都不对B、物理部分1、友谊的小船说翻就翻，假如你不会游泳，就会随着小船一起沉入水底。

2015年清华大学领军计划测试物理学科注意事项：1.2016清华领军计划测试为机考，全卷共100分，考试时间与数学累计120分钟；2.考题全部为不定项选择题，本试卷为回忆版本，故有些问题改编为填空题。

1、（2015领军）在康普顿散射，以下1到5五个区域哪个可能是中心原子存在的区域？（曲线为光子径迹）解：康普顿散射是一个有心力场的运动，与天体运动不同的是其受到的是斥力的作用。

由轨迹我们可知在距离中心原子最近的地方散射粒子的速度不为零，即其角动量不为零。

由角动量守恒知中性粒子只能处于3,4,5三个区域中。

又由对称性可知，中心粒子必处于4区域中。

（2015领军）2、质量为m ，电阻为R 的圆环在如图的磁场磁场中下落，稳定时速度为v 。

求匀速下落时电动势，有以下两种计算方案。

方法一：由受力平衡22B L v mg R= BLv ε=有结论：ε方法二：由功能关系R P mgv =2R P R ε=有结论：ε问：关于以上哪种方案说法正确的是？（ ）A.都正确B.都不正确C.只有方案一正确D.只有方案二正确解：当速度达到稳定时，必然存在受力平衡。

同时功能平衡也是受力平衡的必然要求。

因此两种方案都是正确的。

注：第一方案应说明B 指B 的水平分量（2015领军）3、理想气体做p kV =的准静态过程，已知定容比热v C 和R ，求该过程的比热C（2015领军）4、如图所示，光滑且不计电阻的导轨上有一金属棒，金属棒电阻为R ，初速度为01/v m s =，空间中有恒定的垂直于导轨平面的磁场，磁感应强度为B ，当金属棒减速到010v 时，用时1s 。

速度识别器最低记录是0.001/m s ，求总共记录的该导体棒运动时间为多少？所以2133t t s ==（2015领军）5、高为H 出平抛一物体，同时在其正下方水平地面斜抛一物体，二者同时落到同地，则斜抛物体的射高为______6、（2015领军）有一厚度为D 的透明玻璃砖，一束白光以入射角60︒角射入。

专题之7、解析几何一、选择题。

1．(2009年复旦大学)设△ABC三条边之比AB∶BC∶CA=3∶2∶4,已知顶点A的坐标是(0,0),B的坐标是(a,b),则C的坐标一定是2．(2009年复旦大学)平面上三条直线x−2y+2=0,x−2=0,x+ky=0,如果这三条直线将平面划分成六个部分,则k可能的取值情况是A.只有唯一值B.可取二个不同值C.可取三个不同值D.可取无穷多个值3．(2010年复旦大学)已知常数k1,k2满足0<k1<k2,k1k2=1.设C1和C2分别是以y=±k1(x−1)+1和y=±k2(x−1)+1为渐近线且通过原点的双曲线,则C1和C2的离心率之比等于5．(2011年复旦大学)A.ρsin θ=1B.ρcos θ=−1C.ρcos θ=1D.ρsin θ=−1 6．(2011年复旦大学)设直线L过点M(2,1),且与抛物线y2=2x相交于A,B两点,满足|MA|=|MB|,即点M(2,1)是A,B的连接线段的中点,则直线L的方程是A.y=x−1B.y=−x+3C.2y=3x−4D.3y=−x+5 7．(2011年复旦大学)设有直线族和椭圆族分别为x=t,y=mt+b(m,b为实数,t为参数)和(a是非零实数),若对于所有的m,直线都与椭圆相交,则a,b应满足A.a2(1−b2)≥1B.a2(1−b2)>1C.a2(1−b2)<1D.a2(1−b2)≤1 8．(2011年复旦大学)极坐标表示的下列曲线中不是圆的是A.ρ2+2ρ(cos θ+sin θ)=5B.ρ2−6ρcos θ−4ρsin θ=0C.ρ2−ρcos θ=1D.ρ2cos 2θ+2ρ(cos θ+sin θ)=19.10.(2012年复旦大学)B.抛物线或双曲C.双曲线或椭圆D.抛物线或椭圆A.圆或直线线11．(2011年同济大学等九校联考)已知抛物线的顶点在原点,焦点在x轴上,△ABC的三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC边所在直线的方程为4x+y−20=0,则抛物线方程为A.y2=16xB.y2=8xC.y2=−16xD.y2=−8xA.2B.2C.4D.413．(2011年清华大学等七校联考)AB为过抛物线y2=4x焦点F的弦,O为坐标原点,且∠OFA=135°,C为抛物线准线与x轴的交点,则∠ACB的正切值为14．(2012年清华大学等七校联考)椭圆长轴长为4,左顶点在圆(x−4)2+(y−1)2=4上,左准线为y 轴,则此椭圆离心率的取值范围是二、解答题。

B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3、设A,B 是抛物线y=x 2上的两点，O 是坐标原点．若OA ⊥OB ，则（ ）A ．|OA|⋅|OB|⩾2B ．|OA|+|OB|⩾C ．直线AB 过抛物线y=x 2的焦点D ．O 到直线AB 的距离小于等于14、设函数f (x)的定义域为(−1,1)，且满足：① f (x)>0，x ∈(−1,0)；② ()()()1x yf x f y f xy ++=+，x,y ∈(−1,1)，则f (x)为（ ）A ．奇函数B ．偶函数C ．减函数D ．有界函数5、如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)−kx 有（） A ．2个极大值点B ．3个极大值点C ．2个极小值点D ．3个极小值点6、△ABC 的三边分别为a,b,c ．若c=2，∠C=3π，且sinC+sin(B −A )−2sin2A=0，则（ ） A ． b=2aB ．△ABC 的周长为3C ．△ABC 的面积为33D ．△ABC 的外接圆半径为2337、设函数2()(3)x f x x e =-，则（ ）A ．f (x)有极小值，但无最小值B ．f (x)有极大值，但无最大值C ．若方程f (x)=b 恰有一个实根，则36b e >D ．若方程f (x)=b 恰有三个不同实根，则360b e <<8、已知222{(,)}A x y x y r =+=，222{(,)()()}B x y x a y b r =-+-=，已知A ∩B={(x 1,y 1),(x 2,y 2)}，则（ ）A ．22202a b r <+<B ．1212()()0a x x b y y -+-=C ．12+x x a =，12+y y b =D ．2211=22a b ax by ++9、已知非负实数x,y,z 满足2224423x y z z +++=，则543x y z ++的最小值为（）A ．1B ．2C ．3D ．410、设数列{a n }的前n 项和为S n ，若对任意正整数n ，总存在正整数m ，使得S n =a m ，则（ ）A ．{a n }可能为等差数列B ．{a n }可能为等比数列C ．{a n }的任意一项均可写成{a n }的两项之差D ．对任意正整数n ，总存在正整数m ，使得a n =S m11、运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（ ）A ．甲B ．乙C ．丙D ．丁12、长方体ABCD −A 1B 1C 1D 1中，AB=2，AD=AA 1=1，则A 到平面A 1BD 的距离为（ ）A ．13B ．23C ．2D13、设不等式组22(1)x y y k x ⎧+≤⎪⎨+≤+⎪⎩ 所表示的区域为D ，其面积为S ，则（ ） A ．若S=4，则k 的值唯一B ．若S=1/2，则k 的值有2个C ．若D 为三角形，则0<k ⩽2/3D ．若D 为五边形，则k>414、△ABC 的三边长是2,3,4，其外心为O ，则OA AB OB BC OC CA →→→→→→⋅+⋅+⋅=（ ）A ．0B ．−15C ．−21/2D ．−29/215、设随机事件A 与B 互相独立，且P(B)=0.5，P(A −B)=0.2，则（ ）A ．P(A)=0.4B ．P(B −A)=0.3C ．P(AB)=0.2D ．P(A+B)=0.916、过△ABC 的重心作直线将△ABC 分成两部分，则这两部分的面积之比的（ ）A ．最小值为3/4B ．最小值为4/5C ．最大值为4/3D ．最大值为5/417、从正15边形的顶点中选出3个构成钝角三角形，则不同的选法有（ ）A ．105种B ．225种C ．315种D ．420种18、已知存在实数r ，使得圆周x 2+y 2=r 2上恰好有n 个整点，则n 可以等于（ ）A ．4B ．6C ．8D ．1219、设复数z 满足2|z|⩽|z−1|，则（ ）A ．|z|的最大值为1B ．|z|的最小值为1/3C ．z 的虚部的最大值为2/3D ．z 的实部的最大值为1/320、设m,n 是大于零的实数，向量a=(mcos α, msin α)，b=(ncos β, nsin β)，其中α,β∈[0,2π)．定义向量12)22a αα=，12)22b ββ=，记θ=α−β，则（ ） A ．1122=a a a ⋅B ．11222a b θ⋅⁡C ．2112224a b θ-≥D ．211222+4a bθ≥21、设数列{a n }满足：16a =，13n n n a a n++=，则（ ） A ．∀n ∈N * ，a n <(n+1)3B ．∀n ∈N * ，a n ≠2015C ．∃n ∈N * ，a n 为完全平方数D ．∃n ∈N * ，a n 为完全立方数22、在极坐标系中，下列方程表示的图形是椭圆的有（ ）A ．1cos sin ρθθ=+ B ．12sin ρθ=+ C ．12cos ρθ=- D ．11+2sin ρθ=23、设函数2sin ()1x f x x x π=-+，则（ ） A ． f (x)⩽4/3B ． |f (x)|⩽5|x|C ．曲线y=f (x)存在对称轴D ．曲线y=f (x)存在对称中心24、△ABC 的三边分别为a,b,c ，若△ABC 为锐角三角形，则（ ）A ． sinA>cosBB ． tanA>cotBC ． a 2+b 2>c 2D ． a 3+b 3>c 325、设函数f (x)的定义域是(−1,1)，若f (0)=f ′(0)=1，则存在实数δ∈(0,1)，使得（ ）A ． f (x)>0，x ∈(−δ,δ)B ． f (x)在(−δ,δ)上单调递增C ． f (x)>1， x ∈(0,δ)D ． f (x)>1， x ∈(−δ,0)26、在直角坐标系中，已知A (−1,0)，B(1,0)．若对于y 轴上的任意n 个不同点P 1,P 2,⋯,P n ，总存在两个不同点P i ,P j ，使得|sin ∠AP i B −sin ∠AP j B|⩽1/3，则n 的最小值为（ ）A ．3B ．4C ．5D ．627、设非负实数x,y 满足2x+y=1，则x ） A ．最小值为4/5B ．最小值为2/5C ．最大值为1D ．最大值为13+28、对于50个黑球和49个白球的任意排列（从左到右排成一行），则（ ） A ．存在一个黑球，它右侧的白球和黑球一样多B ．存在一个白球，它右侧的白球和黑球一样多C ．存在一个黑球，它右侧的白球比黑球少一个D ．存在一个白球，它右侧的白球比黑球少一个29、从1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（ ）A ．300个B ．450个C ．900个D ．1800个30、设曲线L 的方程为42242(22)(2)0y x y x x +++-=，则（ ）A ．L 是轴对称图形B ．L 是中心对称图形C ．L ⊂{(x,y)|x 2+y 2⩽1}D ．L ⊂{(x,y)| 12-⩽y ⩽12}2015年清华大学自主招生暨领军计划数学试题参考答案。

微专题30向量投影备考要点向量的数量积是向量的核心概念，是平面向量一章中最精彩的部分，也是历年高考中的高频考点．求定向量与动向量数量积的最值或范围，这类问题若能合理运用数量积的几何意义———向量投影，可回避繁琐的代数运算，解题过程会十分直观和简捷！方法是向定向量作垂线段，若是“双动”模型，则先固定其中一个向量，以定待动，再求投影.（1）b 在a 方向上的投影：cos a b b b e a θ== （e 为a方向上的单位向量）；（2）共线线段的乘积与数量积的关系：（i ）当,OA OB同向时，1;OA OB OA OB = （ii ）当,OA OB反向时，1.OA OB OA OB =-典型精析例1.如图，11122233,,OA B A A B A A B ∆∆∆是边长为2的正三角形，且123,,,O A A A 四点共线，若点3P 是边33A B 上的动点，则13OB OP的取值范围是答案：[]6,8解析:131313cos OB OP OB OP B OP =∠，当3P 位于3A 时,3OP 在1OB方向的投影最小即6cos603,⨯= 此时131313cos 6.OB OP OB OP B OP ⋅=∠= 当3P 位于3B 时,3OP 在1OB方向的投影最大即24cos604+=,此时131313cos 8.OB OP OB OP B OP ⋅=∠=变式1.1.如图，三个边长为2的等边三角形有一条边在同一直线上，边33B C 上有10个不同的点1210,,,P P P ，记2(1,2,10)i i m AB AP i =⋅=，则1210m m m +++ 的值为（）A.153B.45C .603D .180例2.已知平面向量,a b满足4a = ，2b = ，若对任意共面的单位向量e ，记a e b e ⋅+⋅ 的最大值为M ，则M 的最小值等于．变式2.1已知的单位向量1e ，2e ，12,3πe e <>= ，若对任意与1e ，2e 共面的c 满足121c e c e ⋅+⋅≤恒成立，则2c 的最大值是．例3.正方形ABCD 的边长为2，E ，M 分别为BC ，AB 的中点，点P 是以C 为圆心，CE 为半径的圆上的动点，点N 在正方形ABCD 的边上运动，则PM PN ⋅的最小值是．变式3.1已知ABC △中，,2AB AC AB AC ⊥-=，点M 是线段BC 上一点（含端点），且()1AM AB AC ⋅+= ，则AM的取值范围是．变式3.2已知向量a ，b 满足4a = ，10a b ⋅≥ ，则2a b -的最小值是（）A ．1B ．2C ．3D ．4例4.已知向量,,a b c 满足21,b c a ===则()()c a c b -⋅-的最大值是最小值是变式4.1.如图，圆O 是半径为1的圆，12OA =，设,B C 为圆上的任意2个点，则AC BC 的取值范围是()A ．1,38⎡⎤-⎢⎥⎣⎦B ．[]1,3-C ．[]1,1-D ．1,18⎡⎤-⎢⎥⎣⎦变式4.2若平面向量,,a b c满足：1a c ==，2b =，且()0c a b ×-=，则b c -的取值范围是（）A.2,6 B.3,7C .3,5D .[]1,3拓展提升(2015年清华自主招生暨领军计划)已知ABC ∆的三边长是2,3,4，其外心为O ，则OA AB OB BC OC CA ⋅+⋅+⋅=（）A.0 B.15-C .212-D .292-题组练习1.已知向量,a b 满足：||13a = ,||1b = ,|5|12a b -≤，则b 在a 上的投影的取值范围是.A.551313⎡⎤-⎢⎥⎣⎦,B.5113⎡⎤⎢⎥⎣⎦,C .12113⎡⎤⎢⎥⎣⎦,D .5113⎡⎤--⎢⎥⎣⎦,2.设2,60,.OA OB AOB OP OA OB λμ==∠==+且2,λμ+=则OA 在OP 上投影的取值范围是()A.(]1,2-. B.[)1,1-C .()1,0- D.(]1,23.如图，11122233,,OA B A A B A A B ∆∆∆是边长相等的正三角形，且123,,,O A A A 四点共线，若点123,,P P P 分别是边112233,,A B A B A B 上的动点，记113222131,,,I OB OPI OB OP I OB OP ===则（）A.123I I I >>B.231I I I >>C .213I I I >>D .312I I I >>4.如图，圆O 是边长为2的正方形ABCD 的内切圆，若P 、Q 是圆O 上的两个动点，则AP CQ⋅的取值范围是()A ．[3220]--，B ．[3221]---，C ．[50]-，D ．[51]--，5.已知2a =r ，1b c ==r r，则()()a b c b -⋅-r r r r 的最小值为()A ．2-B ．4-C ．6-D ．1-6．设圆M ，圆N 的半径分别为1，2，且两圆外切于点P ，点A ，B 分别是圆M ，圆N 上的两动点，则PA PB ⋅的取值范围是()A ．18,2⎡⎤-⎢⎥⎣⎦B ．316,4⎡⎤-⎢⎣⎦C ．[]8,1-D ．[]16,1-7.若向量,r r a b 满足22()3a b b a +-==r r r r ，且2b ≥r，则r a 在r b 方向上的投影的取值范围是.8.正四面体A BCD -的棱长为2，空间动点P 满足2PB PC += ，则AP AD的取值范围是.9.已知平面向量,,a b c ，3||2,||3,||4,2a b c a b ===⋅= ，则a c b c ⋅+⋅ 的最大值为，最小值为10.设非零向量,,a b c 满足a b a b +=- 且1a b a b c ==++= ，则a ca的取值范围是．11.已知2,1,a b c === 则()()a b c b -⋅-的最大值为______，最小值为______．12.如图，已知等腰直角三角形ABC 中，902C AC ∠=︒=，，两顶点,A C 分别在,x y 正半轴（含原点O ）上运动，,P Q 分别是,AC AB 的中点，则OP OQOQ⋅的取值范围是.13.如图，已知4,90AC BC ACB ==∠= ，M 为BC 的中点，D 为以AC 为直径的圆上一动点，则AM DC ⋅的最大值是.14.已知向量a b ⊥ ，2a b -= ，定义()1c a b λλλ=+-，其中01λ≤≤，若1212c c λ= ，c λ 的取值范围是．15.已知平面向量,,,a b c d 满足1,a b c === 0,a b ⋅= ,c d b c -=⋅ 则a d ⋅的取值范围为.。

清华大学领军计划测试物理学科注意事项：1.答卷前，考生务必将自己的姓名、准考证号、考点名称填写在答题卡上，并在规定位置粘贴考试用条形码。

2.客观题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

主观题用黑色墨水的钢笔或签字笔将答案写在答题卡相应位置上。

答在试卷上的无效。

3.考试结束后，将本试卷和答题卡一并交回。

4.本试题为考生回忆版，有部分缺题【1】质量m 的小球从距轻质弹簧上端h 处自由下落，弹簧的弹性系数为k ，求小球在运动过程中的最大动能max k E 。

已知重力加速度为g 。

【2】一卫星在距赤道20000km 上空运行，求在赤道上的人能观察到此卫星的时间间隙。

已知地球半径6400e R km 。

【3】在粗糙地面上，某时刻乒乓球的运动状态如图所示，判断一段时间后乒乓球的可能运动状况：A 、静止B 、可能向前无滑滚动C 、原地向左滚动D 、原地向右滚动【4】距O 点10m 处有一堵2m 高的墙，同方向11m 处有一堵3m 高的墙，今将一小球（可看作质点）从O 点斜抛，正好落在两墙之间，求斜抛速度可能值。

【5】有一半径为2r 的线圈。

内部磁场分布如图，磁感应强度均为B 。

有一长为4r 的金属杆（横在中间），其电阻为R 。

金属杆的右半边线圈电阻为R ，左半边线圈电阻为2R 。

当两个磁场磁感应强度从B 缓慢变化至0时，求通过右半边的电荷量q 。

【9】有一辆汽车以恒定功率由静止开始沿直线行驶，一定时间t 内走过的路程为s ，求s 与t 的几次方成正比。

【10】有一封闭绝热气室，有一导热薄板将其分为左右体积比1：3的两部分，各自充满同种理想气体，左侧气体压强为3atm ，右侧气体压强为1atm 。

现将薄板抽走，试求平衡以后气体压强【11】如图有一电容，由三块金属板构成，中间填充相对介电常数为ε的介质，中间两块极板面积为S ，真空介电常量为0ε，求此电容的大小。

理科： 1、你最崇拜的一个科学家？为什么？ 2、班级里你最崇拜的一个同学？为什么？ 3、你最喜欢的一个数学公式？为什么？ 4、父亲和母亲哪一个对你的影响比较大？为什么？ 5、公理和定理有什么不同？ 6、“神六”发射的过程中，哪些现象能用物理原理解释？ 7、火箭喷射过程中有什么化学反应？ 8、台风过境哪些地区受到的影响最大？为什么？ 9、杭州到上海的距离，光速需要多少时间？ 10、如果你家里连续几天没人，怎么样才能让花盆里的花不被干死？ 11、为什么三角形的面积是底乘以高除以2？ 12、（面对一浙江考生）从北京到达浙江，光要行驶多长时间？ 13、在电视上，新闻节目主持人和远方记者通话，为何有时会出现远方记者“反应迟钝”、“慢一拍”的情形？ 文科： 1、你怎样理解鲁迅精神的？ 2、鲁迅笔名是怎么来的？ 3、你怎样理解巴金精神的？ 4、巴金的笔名是怎么来的？（部分笔试试题） 【数学】 1、对定义域为R的f(x)，有f(a,b)＝a·f(b)+b·f（a），且|f(x)|≤1，求证：f(x)恒为零。

2、对于空间四边形ABCD，求AC＋BD的最大值。

【物理】 1、德布罗意波是由著名物理学家德布罗意提出的，它告诉了一个物体质量、速度及其德布罗意波长的关系。

已知：电子ME＝9.1×10－31kg，h ＝6.63×10－34，e＝1.6×10－16，现一个点子经过150V加速后，求：（1）求其德布罗意波长，（2）此电子发出的波在何波段？ 【英语】 作文：以“你理想中的父母与孩子关系”写一篇150字左右的作文。

　 注：所有题目均为受访学生回忆文字，可能表述有差异。

■自主招生申请材料有哪些？ 随着自主招生工作的推进，各校对学生申请材料的重视程度增加。

一般，自主招生申请材料除了申请表以外，需附上获奖证书复印件，由学生所在中学提供的申报大学保送生和自主招生中学推荐表（请校长或主管校长签名并盖章），学生高中三年历次期中和期末考试的原始成绩单，高三阶段提供每一次年级统一考试等的学生各种获奖证明。

清华领军2015.4.设函数()f x 的定义域为（-1，1），且满足：①()0,(1,0)f x x >∈-；②()()1x y f x f y f xy ⎛⎫++= ⎪+⎝⎭，(1,1)x y ∈-、，且()f x 为（ ）A.奇函数B.偶函数C.减函数D.有界函数清华领军2015.5.如图，已知直线y kx n =+与曲线()y f x =相切于两点，则()()F x f x kx =-有（ ）A.2个极大值点B.3个极大值点C.2个极小值点D.3个极小值点 同时分入了导数类清华领军2015.23.设函数2sin π()1xf x x x =-+，则（ ）A.4()3f x ≤B.|()|5||f x x ≤C.由线()y f x =存在对称轴D.曲线()y f x =存在对称中心清华领军2015.30.设曲线L 的方程为42242(22)(2)0y x y x x +++-=，则（ ） A.L 是轴对称图形 B.L 是中心对称图形 C.22{(,)|1}L x y x y ⊂+≤ D.11(,)|22L x y y ⎧⎫⊂-≤≤⎨⎬⎩⎭同时分入函数的极值类清华领军2017.15.已知2()f x x ax b =++在(1,1)x ∈-上有两个零点。

求22a b -的取值范围。

A.(0,)+∞B.(0,2)C.(,2)-∞D.(2,2)-清华领军2017.21.满足35(3)40x y x x y ++++=的(,)x y （ ） A.在一条直线上 B.在一条抛物线上 C.为有限个 D.为无限个 分类存疑北大自招2016.1. 求()212log 2x x -++的单调增区间。

1.【解答】1,22⎛⎫ ⎪⎝⎭要求()212log 2x x -++的单调增区间，由12log x 是在()0,+∞上的减函数，故即解2201,2122x x x x ⎧-++>⎪⎛⎫⇒∈⎨ ⎪>⎝⎭⎪⎩北大自招2016.5. 设x ，y ，z 3R ∈，求方程381nnnx y z ++≤，当n →+∞时确定的几何体的体积为________。

北大清华自主招生面试考题(完整版)北大清华自主招生面试考题(完整版)梧桐夜雨1.马克思在《资本论》中论述机器夺走了工人的饭碗时写道：“蒸汽机一开始就是人力的对头”。

请谈谈你的看法。

2.近期房产税、车船税、“馒头税”等均引发社会热议，请谈谈你对纳税与公民权利关系的理解。

3.哈佛大学图书馆墙上写有这样一句话：“请享受无法回避的痛苦”，谈谈你的理解。

4.假如用一种植物比喻中国人的国民性，你会选择什么？为什么？5.有人说：“智慧比体力更重要，成功的关键在于如何使用智慧”，请谈谈你的看法。

6.现在很多家长在高中阶段就把孩子送到国外学习，谈谈你的看法。

7.国家最近规定，中央和省级机构录用公务员，一般情况下都须具有两年以上基层工作经历，不再招收应届毕业生，你对此有何评论。

8.“穷则独善其身，达则兼济天下”，在今天是否还适用？9.目前一些人富裕了但并没感到幸福，谈谈你的看法。

10.有人认为“三纲”(君臣、父子、夫妻)无益，“五常”(仁义礼智信)可取。

试述你的观点。

11.近来续写《红楼梦》又成为社会热点话题。

你认为后人可以续写、仿写、改写经典名著吗？12.古人云“诗画同源”，“诗是无形画，画是有形诗”。

请谈谈你的见解。

13.请从世界历史和国际政治的角度，分析“只有永远的利益，没有永远的朋友”这句话的含义。

14.今年是辛亥革命100周年，海峡两岸将共同举行隆重庆典。

你认为大陆和台湾看待辛亥革命的角度和意义会有什么不同？15.网络带来丰富的信息，但也存在着许多虚假报道和伪装成民意的倾向性意见，你认为政府如何才能从网络上获取真实的社情民意？16.日本政府最近称，由于中国的GDP已经超过日本，所以要大幅削减对华援助，你如何看待此事？17.在鲁迅的小说《祝福》中，“我”作为一个现代知识分子，为什么不告诉祥林嫂“人死后是没有灵魂的”？18.牛顿第一定律可以被实验验证吗？19.“火”被古人当成一种物质元素，今天我们如何认识“火”？20.诗曰：“我看青山多妩媚，料青山看我应如是”，说说你的理解。

清华大学2015年自主招生、领军计划面试真题
自主招生面试真题(部分)
1.知不知道清华学生对PX的讨论？如何评论学生的行为？
2.最喜欢的历史人物是谁？愿意成为他那样的人吗？
3.对清华的经济系有什么了解？
4.假设给你一次穿越的机会，你最希望穿越到什么时候?做什么人?干什么?
5.清华大学的校训是什么?你是如何理解的?如果你被清华大学录取，你如何去践行这一校训?
6.如果你是班长，如何组织一次关于雷锋精神的班级活动?活动内容，请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。

7.是休学创业，还是毕业后创业？
8.要不要休学当老板?
9.考生为父母做过最感动的事，和父母为考生做过的最感动的事。

“领军计划”面试考题(部分)：
1.你对“中国式过马路”怎么看?
2.你对“中国梦”怎么理解?
3.2012年度的五大新闻是什么，如果你是新闻评论员，请对这些新闻事件作出评论。

4.你对“钓鱼岛事件”怎么看?。