材料力学完整课后习题答案

材料力学课后答案第一章材料单向静拉伸载荷下的力学性能一、解释下列名词滞弹性：在外加载荷作用下，应变落后于应力现彖。

静力韧度：材料在静拉仲时单位体积材科从变形到断裂所消耗的功。

弹性极限：试样加载后再卸裁，以不出现残留的永久变形为标准，材料能够完全弹性恢复的最高应力。

比例极限：应力一应变曲线上符合线性关系的最高应力。

包中格效应:指原先经过少量塑性变形，卸载后同向加载，弹性极限（。

P）或屈服强度（。

S）增加；反向加载时弹性极限（。

P）或屈服强度3 s）降低的现象。

解理断裂:沿一定的晶体学平面产生的快速穿晶断裂。

晶体学平面一一解理面，一般是低指数，表面能低的晶面。

解理而:在解理断裂屮具冇低指数，表而能低的品体淫平而。

韧脆转变：材料力学性能从韧性状态转变到脆性状态的现象（冲击吸收功明显下降，断裂机理由微孔聚集型转变微穿晶断裂，断口特征出纤维状转变为结晶状）。

静力韧度：材料在静拉伸时单位体积材料从变形到断裂所消耗的功叫做静力韧度。

是一个强度与塑性的综合指标，是表示静载下材料强度与塑性的最佳配合。

二、金属的弹性模量主要取决于什么？为什么说它是一个对结构不敏感的力学姓能？答案：金屈的弹性模量主要取决于金屈键的本性和原子间的结合力，而材料的成分和组织对它的影响不大，所以说它是一个对组织不皱感的性能指标，这是弹性模量在性能上的主要特点。

改变材料的成分和组织会对材料的强度（如屈服强度、抗拉强度）有显著影响，但对材料的刚度影响不大。

三、什么是包辛格效应，如何解释，它冇什么实际意义？答案：包辛格效应就是指原先经过变形，然后在反向加载时弹性极限或屈服强度降低的现象。

特别是弹性极限在反向加载时几乎下降到零，这说明在反向加载吋犁性变形立即开始了。

包辛格效应可以用位错理论解释。

第一，在原先加载变形时，位错源在滑移而上产生的位错遇到障碍，塞积后便产生了背应力，这背应力反作用于位错源，当背应力（取决于塞积时产生的应力集中）足够大时，可使位错源停止开动。

材料力学第3版习题答案第一章：应力分析1. 某材料在单轴拉伸下的应力-应变曲线显示，当应力达到200 MPa 时，材料发生屈服。

若材料在该应力水平下继续加载，其应力将不再增加，但应变继续增加。

请解释这一现象，并说明材料的屈服强度是多少？答案：这种现象表明材料进入了塑性变形阶段。

在单轴拉伸试验中，当应力达到材料的屈服强度时，材料的晶格结构开始发生滑移，导致材料的变形不再需要额外的应力增加。

因此，即使继续加载，应力保持不变，但应变会因为材料内部结构的重新排列而继续增加。

在本例中，材料的屈服强度是200 MPa。

第二章：材料的弹性行为2. 弹性模量是描述材料弹性行为的重要参数。

若一块材料的弹性模量为210 GPa，当施加的应力为30 MPa时，其应变是多少？答案：弹性模量（E）与应力（σ）和应变（ε）之间的关系由胡克定律描述，即σ = Eε。

要计算应变，我们可以使用公式ε =σ/E。

将给定的数值代入，得到ε = 30 MPa / 210 GPa =1.43×10^-4。

第三章：材料的塑性行为3. 塑性变形是指材料在达到屈服点后发生的永久变形。

如果一块材料在单轴拉伸试验中，其屈服应力为150 MPa，当应力超过这个值时，材料将发生塑性变形。

请解释塑性变形与弹性变形的区别。

答案：塑性变形与弹性变形的主要区别在于材料在去除外力后是否能够恢复原状。

弹性变形是指材料在应力作用下发生的形状改变，在应力移除后能够完全恢复到原始状态，不留下永久变形。

而塑性变形是指材料在应力超过屈服点后发生的不可逆的永久变形，即使应力被移除，材料的形状也不会恢复到原始状态。

第四章：断裂力学4. 断裂韧性是衡量材料抵抗裂纹扩展的能力。

如果一块材料的断裂韧性为50 MPa√m，试样的尺寸为100 mm×100 mm×50 mm，试样中存在一个长度为10 mm的初始裂纹。

请计算在单轴拉伸下，材料达到断裂的临界应力。

材料力学课后答案材料力学是一门研究材料的结构和性质以及力学行为的学科。

以下是材料力学课后习题的答案。

1. 对于一个材料试验样品的拉伸测试，如何计算应力和应变？答：应力是试样受到的外部力除以其截面积，应变是试样的长度变化除以其原始长度。

2. 当一根钢条受到拉伸力时，它的截面积会变大还是变小？为什么？答：当钢条受到拉伸力时，它的截面积会减小。

这是因为外部力导致钢条内部发生塑性变形，使其截面积减小。

3. 什么是杨氏模量？如何计算？答：杨氏模量是表征材料在受到应力时的变形能力的物理量。

它可以通过应力与应变之间的比率来计算，即杨氏模量=应力/应变。

4. 什么是泊松比？如何计算？答：泊松比是一个无量纲的物理量，它描述了材料在拉伸或压缩时的横向收缩量与纵向伸长量之间的比例关系。

它可以通过横向应变与纵向应变之间的比率来计算，即泊松比=横向应变/纵向应变。

5. 什么是屈服强度？如何确定屈服强度？答：屈服强度是材料在受到应力时开始产生塑性变形的应力值。

它可以通过拉伸测试或压缩测试中的应力-应变曲线来确定，屈服强度对应于曲线上的屈服点。

6. 材料的断裂强度是什么？如何计算？答：材料的断裂强度是指材料在受到拉伸或压缩的最大应力值。

它可以通过拉伸测试或压缩测试中的应力-应变曲线来确定，断裂强度对应于曲线上的断裂点。

7. 什么是韧性？如何评价材料的韧性？答：韧性是材料在受力过程中吸收能量的能力。

可以通过材料的断裂能量来评价韧性，断裂能量是在材料断裂前吸收的总能量。

8. 什么是冷加工和热加工？它们对材料性能有何影响？答：冷加工是在室温下对材料进行塑性变形，而热加工是在高温下对材料进行塑性变形。

冷加工会使材料变硬和脆化，而热加工则会使材料变软和韧性增加。

以上是材料力学课后习题的答案，希望对你的学习有所帮助。

如果有任何疑问，请随时向我提问。

材料力学课后习题答案1. 弹性力学。

1.1 问题描述，一根钢丝的弹性模量为200GPa，其截面积为0.01m²。

现在对这根钢丝施加一个拉力，使其产生弹性变形。

如果拉力为2000N，求钢丝的弹性变形量。

解答：根据胡克定律，弹性变形量与拉力成正比，与材料的弹性模量和截面积成反比。

弹性变形量可以用以下公式计算：$$。

\delta = \frac{F}{AE}。

$$。

其中，$\delta$表示弹性变形量，F表示拉力，A表示截面积，E表示弹性模量。

代入已知数据，可得：$$。

\delta = \frac{2000N}{0.01m² \times 200GPa} = 0.001m。

$$。

所以，钢丝的弹性变形量为0.001m。

1.2 问题描述，一根长为1m，截面积为$10mm^2$的钢棒，两端受到拉力为1000N的作用。

求钢棒的伸长量。

解答：根据胡克定律，钢棒的伸长量可以用以下公式计算：$$。

\delta = \frac{F \cdot L}{AE}。

$$。

其中，$\delta$表示伸长量，F表示拉力，L表示长度，A表示截面积，E表示弹性模量。

代入已知数据，可得：$$。

\delta = \frac{1000N \times 1m}{10mm² \times 200GPa} = 0.005m。

$$。

所以，钢棒的伸长量为0.005m。

2. 塑性力学。

2.1 问题描述，一块金属材料的屈服强度为300MPa，现在对其施加一个拉力，使其产生塑性变形。

如果拉力为500MPa，求金属材料的塑性变形量。

解答：塑性变形量与拉力成正比，与材料的屈服强度无关。

塑性变形量可以用以下公式计算：$$。

\delta = \frac{F}{A}。

$$。

其中，$\delta$表示塑性变形量，F表示拉力，A表示截面积。

代入已知数据，可得：$$。

\delta = \frac{500MPa}{300MPa} = 1.67。

材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。

1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4．包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面。

6．塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

脆性：指金属材料受力时没有发生塑性变形而直接断裂的能力韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b的台阶。

8.河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。

是解理台阶的一种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂，因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内，可以是韧性断裂，也可以是脆性断裂。

沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂。

11.韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变2、说明下列力学性能指标的意义。

答：E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标？答：主要决定于原子本性和晶格类型。

合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小，但是不改变金属原子的本性和晶格类型。

材料力学课后答案1. 弹性力学基础题。

题目，一根长为L的均匀横截面圆柱形杆，端部固定，另一端受力F，求受力端的应变。

解答，根据弹性力学的基本公式，应变ε=σ/E，其中σ为应力，E为弹性模量。

由于杆的横截面积为A，受力F导致的应力σ=F/A。

因此，受力端的应变ε=F/(AE)。

2. 弹性力学应用题。

题目，一根钢丝的长度为L，直径为d，受力F时产生的应力为σ，求其应变。

解答，首先计算钢丝的横截面积A=πd^2/4，然后根据应变ε=σ/E，其中E为钢的弹性模量，求得应变ε=σ/(E)。

3. 材料的破坏。

题目，一块材料在受力时产生的应力达到了其屈服强度，求此时的应变。

解答，当材料的应力达到屈服强度时，材料开始发生塑性变形，此时的应变无法简单地通过弹性力学公式来计算。

需要通过材料的本构关系来确定应变。

4. 弯曲应力与应变。

题目，一根横截面为矩形的梁，在受力时产生的最大应力为σ，求其最大应变。

解答，根据梁的弯曲应力公式σ=My/I，其中M为弯矩，y为梁的截面离中性轴的距离，I为梁的惯性矩。

最大应变发生在最大应力处，由应变ε=σ/E，可以求得最大应变。

5. 拉伸与压缩。

题目，一根长为L的杆在受拉力F时产生的应变为ε，求其长度变化量。

解答，根据胡克定律，拉伸或压缩材料的长度变化量ΔL=εL。

6. 应变能。

题目，一根长为L的弹簧，在受力F时产生的应变为ε，求其弹性势能。

解答，弹簧的弹性势能U=1/2kε^2，其中k为弹簧的弹性系数。

根据ε=F/(kL)，代入可得弹性势能U=1/2F^2/(kL)。

7. 疲劳破坏。

题目，一根金属材料在受到循环载荷时，经过了n次循环后发生疲劳破坏，求其疲劳寿命。

解答，根据疲劳寿命公式N=K(σ_max)^(-1/α)，其中N为疲劳寿命，K为材料常数，σ_max为循环载荷的最大应力，α为材料的疲劳指数。

代入循环载荷的应力值，可以求得疲劳寿命。

8. 蠕变。

题目，一根材料在高温下受到持续载荷时发生了蠕变，求其蠕变应变。

材料力学第五版课后习题答案1. 弹性力学基本概念。

1.1 什么是应力？什么是应变？应力是单位面积上的内力，是描述物体内部受力情况的物理量；而应变则是物体单位长度的形变量，描述了物体在受力作用下的形变情况。

1.2 什么是胡克定律？胡克定律是描述弹性体在弹性变形范围内应力与应变成正比的关系，即应力与应变成线性关系。

1.3 什么是弹性模量？弹性模量是描述物体在受力作用下的变形程度的物理量，通常用E表示，单位是帕斯卡（Pa）。

2. 线弹性力学。

2.1 什么是轴向力？什么是轴向变形？轴向力是指作用在物体轴向的力，轴向变形是指物体在受到轴向力作用下的形变情况。

2.2 什么是泊松比？泊松比是描述物体在轴向受力作用下，横向变形与轴向变形之间的比值，通常用ν表示。

2.3 什么是弯曲应力？什么是弯曲变形？弯曲应力是指物体在受到弯矩作用下的内部应力情况，弯曲变形是指物体在受到弯矩作用下的形变情况。

3. 弹性力学的能量法。

3.1 什么是弹性势能？弹性势能是指物体在受力变形后，能够恢复原状时所具有的能量，通常用U表示。

3.2 什么是弹性线性势能？弹性线性势能是指物体在弹性变形范围内，弹性势能与形变量成线性关系的势能。

3.3 什么是弹性势能密度？弹性势能密度是指单位体积或单位质量物体所具有的弹性势能，通常用u表示。

4. 弹塑性力学。

4.1 什么是屈服点？屈服点是指物体在受力作用下，开始出现塑性变形的临界点。

4.2 什么是屈服应力？屈服应力是指物体在受力作用下开始发生塑性变形时所具有的应力大小。

4.3 什么是塑性势能？塑性势能是指物体在受到超过屈服应力的作用下，发生塑性变形所具有的能量。

5. 薄壁压力容器。

5.1 什么是薄壁压力容器？薄壁压力容器是指壁厚相对于容器直径而言很小的压力容器。

5.2 薄壁压力容器的内、外压力对容器的影响有哪些？内压力会使容器产生膨胀变形，而外压力会使容器产生收缩变形。

5.3 薄壁压力容器的应力分布情况是怎样的？薄壁压力容器内外表面的应力分布情况是不均匀的，通常集中在壁厚的两侧。

8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

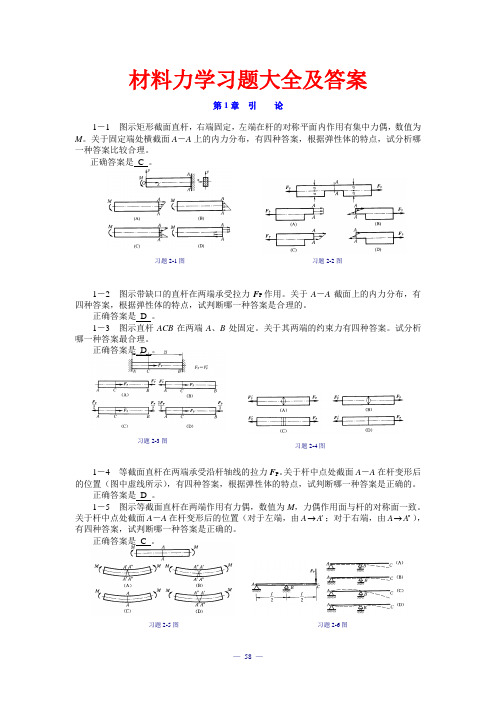
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

习题2-1图习题2-2图习题2-3图习题2-4图1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）d d Q x F d M（B ）d d Q x F （C ）d d Q x F （D ）d d Q xF 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。

材料力学第二版课后答案1. 弹性力学。

1.1. 什么是材料的弹性？材料的弹性是指材料在受力后能够恢复原状的性质。

当外力作用于材料上时，材料会发生形变，但在去除外力后，材料会恢复到原来的形状和尺寸。

1.2. 什么是胡克定律？胡克定律是描述弹性体在弹性变形时，应力和应变之间的关系。

它可以用数学公式表示为，σ = Eε，其中σ表示应力，E表示弹性模量，ε表示应变。

1.3. 什么是杨氏模量？杨氏模量是描述材料抗拉伸性能的指标，它表示单位面积内的拉应力增加一个单位的长度时，材料的伸长量。

杨氏模量的计算公式为，E = σ/ε。

2. 塑性力学。

2.1. 什么是材料的塑性？材料的塑性是指材料在受力后会发生永久性变形的性质。

当外力作用于材料上时，材料会发生塑性变形，去除外力后，材料无法完全恢复原状。

2.2. 什么是屈服点？屈服点是材料在受力过程中，应力-应变曲线上的一个特殊点，表示材料从弹性变形进入塑性变形的临界点。

在屈服点之后，材料会发生永久性变形。

2.3. 什么是材料的硬度？材料的硬度是指材料抵抗外力压入的能力。

硬度测试可以用来评价材料的耐磨性、耐压性等性能，常用的硬度测试方法包括洛氏硬度、巴氏硬度等。

3. 断裂力学。

3.1. 什么是断裂韧性？断裂韧性是材料抵抗断裂的能力。

它是指材料在受到外力作用时，能够吸收大量的能量而不发生断裂的能力。

3.2. 什么是脆性断裂？脆性断裂是材料在受力过程中，发生迅速、不可逆的断裂现象。

脆性断裂的特点是断裂前往往不伴随明显的塑性变形。

3.3. 什么是韧性断裂？韧性断裂是材料在受力过程中，发生缓慢、可逆的断裂现象。

韧性断裂的特点是断裂前伴随明显的塑性变形，能够吸收大量的能量。

4. 疲劳力学。

4.1. 什么是疲劳寿命？疲劳寿命是指材料在受到交变应力作用下，经过一定次数的循环载荷后发生疲劳断裂的次数。

4.2. 什么是疲劳强度？疲劳强度是指材料在受到交变应力作用下，能够承受的最大应力水平，也可以理解为材料的抗疲劳能力。

材料力学第五版课后习题答案Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d)解：。

2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4）应力是内力分布集度。

（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6）若物体产生位移，则必定同时产生变形。

（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。

（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。

（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。

（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。