材料力学习题解答

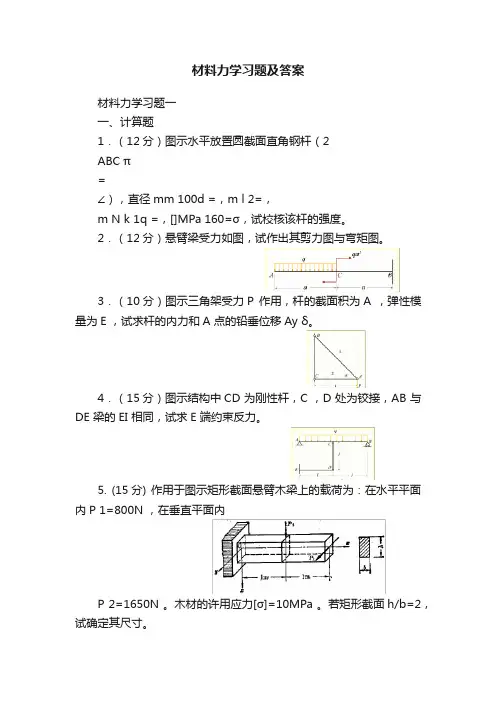
材料力学习题及答案材料力学习题一一、计算题1．（12分）图示水平放置圆截面直角钢杆（2ABC π=∠），直径mm 100d =，m l 2=，m N k 1q =，[]MPa 160=σ，试校核该杆的强度。

2．（12分）悬臂梁受力如图，试作出其剪力图与弯矩图。

3．（10分）图示三角架受力P 作用，杆的截面积为A ，弹性模量为E ，试求杆的内力和A 点的铅垂位移Ay δ。

4．（15分）图示结构中CD 为刚性杆，C ，D 处为铰接，AB 与DE 梁的EI 相同，试求E 端约束反力。

5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为：在水平平面内P 1=800N ，在垂直平面内P 2=1650N 。

木材的许用应力[σ]=10MPa 。

若矩形截面h/b=2，试确定其尺寸。

三．填空题（23分）1．（4分）设单元体的主应力为321σσσ、、，则单元体只有体积改变而无形状改变的条件是＿＿＿＿＿＿＿＿＿＿；单元体只有形状改变而无体积改变的条件是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

2．（6分）杆件的基本变形一般有＿＿＿＿＿＿、＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿四种；而应变只有＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿两种。

3．（6分）影响实际构件持久极限的因素通常有＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿，它们分别用＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿＿来加以修正。

4.（5分）平面弯曲的定义为＿＿＿＿＿＿＿＿＿＿＿＿_＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿_。

5.（2分）低碳钢圆截面试件受扭时，沿＿＿＿＿＿＿＿＿＿＿＿＿截面破坏；铸铁圆截面试件受扭时，沿＿＿＿＿＿＿＿＿＿＿＿＿面破坏。

四、选择题（共2题，9分）2．（5分）图示四根压杆的材料与横截面均相同，试判断哪一根最容易失稳。

答案：（）材料力学习题二二、选择题：（每小题3分，共24分）1、危险截面是______所在的截面。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。

材料力学习题答案1(总26页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--材料力学习题答案1试求图各杆1-1、2-2、3-3 截面上的轴力，并作轴力图。

解：(a) ()1140302050F kN -=+-=，()22302010F kN -=-=，()3320F kN -=-(b) 11F F -=，220F F F -=-=，33F F -=(c) 110F -=，224F F -=，3343F F F F -=-=轴力图如题2. 1 图( a) 、( b ) 、( c) 所示。

作用于图示零件上的拉力F=38kN ，试问零件内最大拉应力发生在哪个截面上 并求其值。

解 截面1-1 的面积为()()21502220560A mm =-⨯=截面2-2 的面积为()()()2215155022840A mm =+-=因为1-1截面和2-2 截面的轴力大小都为F ，1-1截面面积比2-2 截面面积小，故最大拉应力在截面1-1上，其数值为：()3max 11381067.9560N F F MPa A A σ⨯====冷镦机的曲柄滑块机构如图所示。

镦压工件时连杆接近水平位置，承受的镦压力F=1100kN 。

连杆截面是矩形截面，高度与宽度之比为 1.4hb=。

材料为45钢，许用应力[]58MPa σ=，试确定截面尺寸h 及b 。

解 连杆内的轴力等于镦压力F ，所以连杆内正应力为F Aσ=。

根据强度条件，应有[]F F A bh σσ==≤，将1.4h b=代入上式，解得()()0.1164116.4b m mm ≥== 由 1.4h b=，得()162.9h mm ≥所以，截面尺寸应为()116.4b mm ≥，()162.9h mm ≥。

在图示简易吊车中，BC 为钢杆，AB为木杆。

木杆AB 的横截面面积21100A cm =，许用应力[]17MPa σ=；钢杆BC 的横截面面积216A cm =，许用拉应力[]2160MPa σ=。

材料力学习题册参考答案材料力学习题册参考答案（无计算题）第1章：轴向拉伸与压缩一：1（ABE ）2（ABD ）3（DE ）4（AEB ）5（C ）6（ＣＥ）７（ABD ）8（C ）9（BD ）10（ADE ）11（ACE ）12（D ）13（CE ）14（D ）15（ＡＢ）１６（BE ）17（D ）二：1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三：1：钢铸铁 2：比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =， EAFl l =5.强度，刚度，稳定性；6.轴向拉伸（或压缩）；7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形，加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案：1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <；< 剪切挤压答案：一：1.（C ），2.（B ），3.（A ），二：1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章：扭转一：1.（B ） 2.（C D ） 3.（C D ） 4. （C ） 5. （A E ） 6. （A ）7. （D ）8. （B D ） 9.（C ） 10. （B ） 11.（D ） 12.（C ）13.（B ）14.（A ） 15.（A E ）二：1错 2对 3对 4错 5错 6 对三：1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路（剪力流）第3章：平面图形的几何性质一：1.（C ），2.（A ），3.（C ），4.（C ），5.（A ），6.（C ），7.（C ），8.（A ），9.（D ）二：1）. 1；无穷多；2）4)4/5(a ； 3），84p R I π=p 4z y I 16R I I ===π4）12/312bh I I z z ==；5）)/(/H 6bh 6BH W 32z -= 6）12/)(2211h b bh I I I I z y z y +=+=+；7）各分部图形对同一轴静矩8）两轴交点的极惯性矩；9）距形心最近的；10）惯性主轴；11）图形对其惯性积为零三：1：64/πd 114； 2.（0 , 14.09cm ）(a 22，a 62)3： 4447.9cm 4， 4：0.00686d 4 ，5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章：弯曲内力一：1.（A B ）2.（D ）3.（B ）4.（A B E ）5.（A B D ）6.（ACE ） 7.（ABDE ） 8.（ABE ）9. （D ） 10. （D ） 11.（ACBE ） 12.（D ） 13.（ABCDE ）二：1错 2错 3错 4对 5错 6对 7对三：1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章：弯曲应力一：1（ＡＢＤ）２．（C ）3.（BE ）4.（A ）5.（C ）6.（C ）7.（B ）8.（C ）9.（BC ）二：1对 2错 3错 4 对 5 错 6错 7 对三：1.满足强度要求更经济、更省料2. 变成曲面，既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章：弯曲变形一：1（B ），2（B ），3（A ），4（D ），5（C ），6（A ），7（C ），8（B ），9（A ）10（B ），11（A ）二：1对2错3错4错5错6对7错8错9错10对11错12对三：1.（转角小量:θθtan ≈）（未考虑高阶小量对曲率的影响）2. 挠曲线采用近似微分方程导致的。

习题2-2一打入基地内的木桩如图所示，杆轴单位长度的摩擦力fkx2，试做木桩的后力图。

解：由题意可得：l 1 0 fdx F 有kl 3 F k 3F / l 3 3 l FN x1 3Fx 2 / l 3dx F x1 / l 3 0习题2-3 石砌桥墩的墩身高l 10m ，其横截面面尺寸如图所示。

荷载 F 1000kN ，材料的密度2.35kg / m 3 ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：N F G F Alg 2-3 图1000 3 2 3.14 12 10 2.35 9.8 3104.942kN 墩身底面积： A 3 2 3.14 12 9.14m 2 因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

N 3104.942kN 339.71kPa 0.34MPa A 9.14m 2习题2-7 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7 图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：Fdx l F F l dx d l ，l dx EA x 0 EA x E 0 A x r r1 x r r d d1 d ，r 2 1 x r1 2 x 1 ，r2 r1 l l 2l 2 d d1 d d1 d d1 2 d d A x 2 x 1 u2 ，d 2 x 1 du 2 dx 2l 2 2l 2 2l 2l 2l dx d d 2l du dx du ，2 2 1 du 2 d 2 d1 A x u d1 d 2 u l F F l dx 2 Fl l du 因此，l dx 0 u 2 0 EA x E 0 A x E d1 d 2 l 2 Fl 1 l 2 Fl 1 u E d d d d E d1 d 2 0 2 2 d 1 1 x 1 2l 2 0 2 Fl 1 1 E d1 d 2 d 2 d 1 dd1 l 1 2l 2 2 2 Fl 2 2 4 Fl E d1 d 2 d 2 d1 Ed 1 d 2习题2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。

材料力学课后习题答案1. 弹性力学。

1.1 问题描述，一根钢丝的弹性模量为200GPa，其截面积为0.01m²。

现在对这根钢丝施加一个拉力，使其产生弹性变形。

如果拉力为2000N，求钢丝的弹性变形量。

解答：根据胡克定律，弹性变形量与拉力成正比，与材料的弹性模量和截面积成反比。

弹性变形量可以用以下公式计算：$$。

\delta = \frac{F}{AE}。

$$。

其中，$\delta$表示弹性变形量，F表示拉力，A表示截面积，E表示弹性模量。

代入已知数据，可得：$$。

\delta = \frac{2000N}{0.01m² \times 200GPa} = 0.001m。

$$。

所以，钢丝的弹性变形量为0.001m。

1.2 问题描述，一根长为1m，截面积为$10mm^2$的钢棒，两端受到拉力为1000N的作用。

求钢棒的伸长量。

解答：根据胡克定律，钢棒的伸长量可以用以下公式计算：$$。

\delta = \frac{F \cdot L}{AE}。

$$。

其中，$\delta$表示伸长量，F表示拉力，L表示长度，A表示截面积，E表示弹性模量。

代入已知数据，可得：$$。

\delta = \frac{1000N \times 1m}{10mm² \times 200GPa} = 0.005m。

$$。

所以，钢棒的伸长量为0.005m。

2. 塑性力学。

2.1 问题描述，一块金属材料的屈服强度为300MPa，现在对其施加一个拉力，使其产生塑性变形。

如果拉力为500MPa，求金属材料的塑性变形量。

解答：塑性变形量与拉力成正比，与材料的屈服强度无关。

塑性变形量可以用以下公式计算：$$。

\delta = \frac{F}{A}。

$$。

其中，$\delta$表示塑性变形量，F表示拉力，A表示截面积。

代入已知数据，可得：$$。

\delta = \frac{500MPa}{300MPa} = 1.67。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。

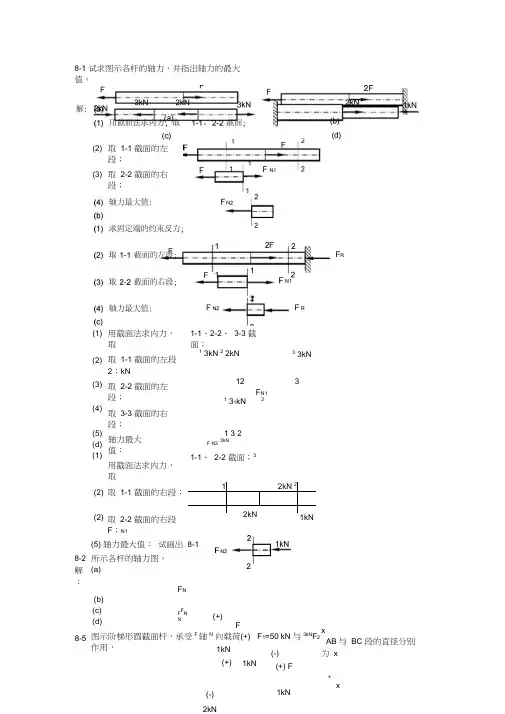
xx8-1 试求图示各杆的轴力，并指出轴力的最大值。

取 1-1 截面的左段；(2) (3) F N1取 2-2 截面的右段；F R用截面法求内力，取1-1、2-2、 3-3 截面；(1) (2) (3) (4)(5)(d)(1)取 1-1 截面的左段2；kN 取 2-2 截面的左段；取 3-3 截面的右段；轴力最大值： 用截面法求内力，取13kN 2 2kN33kN12 3F N11 31kN 21 32 F N33kN1-1、 2-2 截面；38-2 解：8-5 (2) (2) 取 1-1 截面的右段； 取 2-2 截面的右段F ；N112kN 22kN(5) 轴力最大值： 试画出 8-1所示各杆的轴力图。

(a) (b) (c) (d)F NF FN N(+)F图示阶梯形圆截面杆，承受F 轴N 向载荷(+) F 1=50 kN 与3kNF 2作用， 1kN (+) 1kN(-)(+) Fx AB 与 BC 段的直径分别为 x (-)1kN2kNd 1=20 mm 和 d 2=30 mm ，如欲使 AB 与 BC 段横截面上的正应力相同，试求载荷 F 2 之值。

(2) 求 1-1、 2-2 截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷 F=10 kN 作用，杆的横截面面积 A=1000 mm 2，粘接面的方位 角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

l 1l 2解： (1) 用截面法求 AB 、 BC 段的轴力；(2) 分段计F 算个杆向变形；FAC 杆缩短。

2F8-22 图示桁架，杆 1与A 杆 2的横截面面积与材料均相B 同，在节点 A 处承受C 载荷 F 作用。

从解： 8-6 解： (1) 用截面法求出 F 11-1、2-2 截面的轴力；(2) 求 1-1、 2-2 截面的正应A 力 ，利用正应力相B 同 ；题 8-5 图所示圆截面杆，已知载荷 1F 1=200 kN ，F 2=1020 kN ，CAB 段的直径 d 1=40 mm ，如 欲使 AB 与 BC 段横截面上的正应力相同，试求 BC 段的直径。

材料力学作业解答1.弹簧的力学行为弹簧是一种具有弹性的材料，它可以在受力时发生弹性形变，并且能够恢复到原始形状。

弹簧的力学行为可以通过胡克定律来描述。

根据胡克定律，弹簧的形变与施加在它上面的力成正比，即F=k*x，其中F是施加在弹簧上的力，k是弹簧的弹性系数，x是弹簧的形变量。

2.弹簧的应变能和弹性势能当弹簧被拉伸或压缩时，它会储存一定量的应变能。

弹簧的应变能可以通过下式计算：U=(1/2)*k*x^2，其中U是弹簧储存的应变能，k是弹簧的弹性系数，x是弹簧的形变量。

3.伸长弹簧的应变能假设一个弹簧的弹性系数为k，它被拉伸或压缩x长度。

根据胡克定律，施加在弹簧上的力可以通过F = k * x计算得到。

通过积分力在形变路径上的关系，可以得到弹簧的应变能。

假设初始长度为L，拉伸后的长度为L+x，则弹簧的伸长应变能可以计算如下：U = ∫[0, L+x] F(x)dx = ∫[0, x] k * x dx = (1/2) k * x^24.剪切应力和剪切应变剪切应力是作用于物体上的横截面内的剪切力与该横截面上的面积之比。

剪切应变是物体在受到剪切应力时产生的形变。

剪切应力和剪切应变之间的关系可以通过剪切弹性模量来描述。

剪切弹性模量G可以通过下式计算：G=τ/γ，其中τ是剪切应力，γ是剪切应变。

5.弯曲应力和弯曲应变弯曲应力是作用于物体上的弯曲力与该物体的横截面想对距离之比。

弯曲应变是物体在受到弯曲应力时产生的形变。

弯曲应力和弯曲应变之间的关系可以通过弯曲弹性模量来描述。

弯曲弹性模量E可以通过下式计算：E=σ/ε，其中σ是弯曲应力，ε是弯曲应变。

6.斯特拉因准则斯特拉因准则描述了材料在达到破坏点之前的应力和应变行为。

根据斯特拉因准则，当材料达到其屈服点时，应力和应变之间的关系可以通过单一的线性方程来描述。

这个线性方程表明了在屈服点之前，应力与应变之间的比例关系。

7.杨氏模量和泊松比杨氏模量是一种描述材料刚度的量度，它可以表示应力与应变之间的比例关系。

习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

习题2-1图习题2-2图习题2-3图习题2-4图1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）d d Q x F d M（B ）d d Q x F （C ）d d Q x F （D ）d d Q xF 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。

绪 论一、 是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。

（ ） 1.2 内力只能是力。

（ ）1.3 若物体各点均无位移，则该物体必定无变形。

（ ） 1.4 截面法是分析应力的基本方法。

（ ） 二、选择题1.5 构件的强度是指（ ），刚度是指（ ），稳定性是指（ ）。

A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设，可认为构件的（ ）在各点处相同。

A. 应力 B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是（ ） A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力参考答案：1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1. 等截面直杆CD 位于两块夹板之间，如图示。

杆件与夹板间的摩擦力与杆件自重保持平衡。

设杆CD 两侧的摩擦力沿轴线方向均匀分布，且两侧摩擦力的集度均为q ，杆CD 的横截面面积为A ，质量密度为ρ，试问下列结论中哪一个是正确的？ (A) q gA ρ=；(B) 杆内最大轴力N max F ql =； (C) 杆内各横截面上的轴力N 2gAlF ρ=；(D) 杆内各横截面上的轴力N 0F =。

2. 低碳钢试样拉伸时，横截面上的应力公式N F A σ=适用于以下哪一种情况? (A) 只适用于σ≤p σ； (B) 只适用于σ≤e σ； (C)3. 在A 和B和点B 的距离保持不变，绳索的许用拉应力为[]σ取何值时，绳索的用料最省？ (A) 0； (B) 30； (C) 45； (D) 60。

4. 桁架如图示，载荷F 可在横梁（刚性杆）DE 为A ，许用应力均为[]σ（拉和压相同）。

求载荷F 的许用值。

以下四种答案中哪一种是正确的？(A)[]2A σ； (B) 2[]3Aσ；(C) []A σ； (D) 2[]A σ。

1、晶胞：晶胞是能代表晶格中原子排列规律的最小几何单元。

2、同素异构转变：固态金属的晶格结构随温度改变而改变的现象。

3、固溶强化：通过溶入溶质元素形成固溶体，使材料的强度、硬度提高的现象。

4、钢的淬透性：在规定条件下，钢在淬火时获得淬硬层（淬透层）深度的能力。

5、调质处理：把淬火和高温回火相结合的热处理方法称为调质处理。

1、单晶体：如果一块晶体，其内部的晶格位向完全一致，则称这块晶体为单晶体。

2、共晶反应：指一定成分的液体合金，在一定温度下，同时结晶出成分和晶格均不相同的两种晶体的反应。

3、相：在合金中，具有同一化学成分、同一晶体结构，且有界面与其它部分分开的均匀组成部分。

4、回火脆性：在某温度范围内回火时，冲击韧性会出现下降的现象，称为回火脆性。

5、马氏体：碳在α－Fe中的过饱和固溶体。

1、抗拉强度：材料在拉伸载荷下抵抗最大均匀塑性变形的能力。

2、固溶体：合金的组元之间以不同的比例混合，形成一种与某一组元晶格相同，并包含其它组元的合金固相，这种相称为固溶体。

3、热加工：金属在再结晶温度以上进行的加工。

4、钢的淬透性：在规定条件下，钢在淬火时获得淬硬层（淬透层）深度的能力。

5、表面淬火：仅将钢件表层快速加热至奥氏体化，然后迅速冷却，不改变心部组织的淬火方法。

1、热处理：指钢在固态下，进行加热、保温和冷却，以改变钢的内部组织结构，从而获得所需性能的一种工艺方法。

2、再结晶：冷变形的金属被加热到较高的温度时，破碎拉长的晶粒变成新的等轴晶粒，内应力、强度和硬度显著下降，塑性显著增加这样的过程。

3、合金：将一种金属同一种或几种其他元素结合在一起所组成的有金属特性的物质。

4、弥散强化：当金属化合物以极小的粒子均匀分布在固溶体基体上时，能提高合金的强度、硬度和耐磨性，而其塑性、韧性降低不多的现象。

5、回火稳定性：又叫耐回火性，即淬火钢在回火过程中抵抗硬度下降的能力。

1．晶体各向异性：晶体中不同晶面或晶向上的原子密度不同，造成晶体不同方向上的性能不同的现象。

第二章 轴向拉伸与压缩2-1 试求图示直杆横截面1-1、2-2、3-3上的轴力，并画出轴力图。

F N (kN)F N1= -2kN F N2 = 0kN F N3= 2kN(a (b )2-2 图示中部对称开槽直杆，试求横截面1-1和2-2上的正应力。

解： 1．轴力由截面法可求得，杆各横截面上的轴力为 kN 14N -=-=F F 2．应力4201014311N 11⨯⨯-==--A F σMPa 175-=MPa ()410201014322N 22⨯-⨯-==--A F σMPa 350-=MPa2-3 图示桅杆起重机，起重杆AB 的横截面是外径为mm 20、内径为mm 18的圆环，钢丝绳BC 的横截面面积为2mm 10。

试求起重杆AB 和钢丝绳BC=2kN解： 1．轴力取节点B 为研究对象，受力如图所示，0=∑x F ： 045cos 30cos N N =++ F F F AB BC 0=∑y F ： 045sin 30sin N =-- F F AB由此解得： 83.2N -=AB F kN ， 04.1N =BC F kN 2．应力起重杆横截面上的应力为 ()223N 182041083.2-⨯⨯-==πσAB AB ABA F MPa 4.47-=MPa 钢丝绳横截面上的应力为101004.13N ⨯==BC BC BCA F σMPa 104=MPa2-4 图示由铜和钢两种材料组成的等直杆，铜和钢的弹性模量分别为GPa 1001=E 和GPa 2102=E 。

若杆的总伸长为mm 126.0Δ=l ，试求载荷F 和杆横截面上的应力。

解：1．横截面上的应力 由题意有⎪⎪⎭⎫⎝⎛+=+=∆+∆=∆2211221121E l E l A E Fl A E Fl l l l σ 由此得到杆横截面上的应力为铜钢3322111021040010100600126.0⨯+⨯=+∆=E l E l l σMPa 9.15=MPa2．载荷24049.15⨯⨯==πσA F N 20=kN2-5 图示阶梯形钢杆，材料的弹性模量GPa 200=E ，试求杆横截面上的最大正应力和杆的总伸长。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M 的力偶作用。

试问在杆件的任一横截面m-mxx存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量Mx，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-mxx，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝pcosα=120×cos10°=118.2MPaτ＝psinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力FN=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩Mz=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) FNAB=F, FNBC=0, FN，max=F(b) FNAB=F, FNBC=－F, FN，max=F(c) FNAB=－2 kN, FN2BC=1 kN, FNCD=3 kN, FN，max=3 kN(d) FNAB=1 kN, FNBC=－1 kN, FN，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。