当前位置：文档之家 › 材料力学II习题解答 最终版

材料力学II习题解答 最终版

  • 格式：pdf
  • 大小：527.78 KB
  • 文档页数：63

下载文档原格式

  / 63

合集下载

材料力学第2版 课后习题答案 第7章 弯曲变形

材料力学第2版 课后习题答案 第7章 弯曲变形

250
−qx l⎞ ⎛ 9l 3 − 24lx 2 + 16 x 3 ) ⎜ 0 ≤ x ≤ ⎟ ( 384 EJ 2⎠ ⎝ − ql ⎛l ⎞ y2 = −l 3 + 17l 2 x − 24lx 2 + 8 x 3 ) ⎜ ≤ x ≤ l ⎟ ( 384 EJ ⎝2 ⎠
y1 =
41ql 4 ( x = 0.25l ) 1536 EJ 5ql 4 ⎛l⎞ y⎜ ⎟ = − 768EJ ⎝2⎠
习 题 7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI为常量。
7－1 （a） M( x) = M 0
∴ EJy '' = M 0 1 EJy ' = M 0 x + C EJy = M 0 x 2 + Cx + D 2 边界条件: x = 0 时 y = 0 ； y' = 0
代入上面方程可求得：C=D=0
（c）
l−x q0 l q0 1 3 ⎛l−x⎞ M ( x) = − q( x) ( l − x ) ⎜ ⎟ = − ( l − x) 2 6l ⎝ 8 ⎠ q 3 ∴ EJy '' = 0 ( l − x ) 6l q 4 EJy ' = − 0 ( l − x ) + C 24l q 5 EJy = 0 ( l − x ) + Cx + D 120l y = 0 ； y' = 0 边界条件： x = 0 时 q( x) =
）
（c）解：
q0 x l q x2 EJy ''' = 0 + C 2l q0 x3 '' EJy = + Cx + D 6l q x 4 Cx 2 EJy ' = 0 + + Dx + A 24l 2 q0 x5 Cx 3 Dx 2 ' EJy = + + + Ax + B 120l 6 2 ⎧y=0 ⎧y=0 边界条件： x = 0 ⎨ '' x = l ⎨ '' ⎩y = 0 ⎩y = 0 ql D=0 ∴C = − 0 6 7q l 3 A= 0 B=0 360 EJy '''' =

工程力学2(材料力学)习题解答

工程力学2(材料力学)习题解答

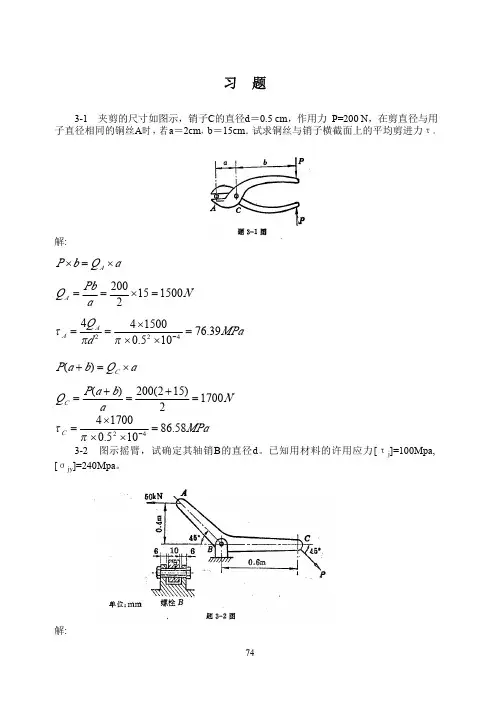
《工程力学2习题解答》建筑1001班陈飞力学教研室编著1-2. 试求图示结构mm 和nn 两截面上的内力，并指出AB 和BC 两杆属何种基本变形。

解：（1）求约束反力：取杆AB 为研究对象∑∑∑=⨯-⨯==-+===0233 003 000BCABCAAN M N Y Y X X 解得：kN Y kN N A BC 1 2==（2）求m-m 截面内力：将杆AB 沿截面m-m 截开, 取左半部分kNm Y M kN Y Q A m-m A m m 11 1=⨯===-AB 杆发生弯曲变形。

（3）求n-n 截面内力：取杆BC 为研究对象，截开n-n 截面kN N N BC n n 2==-BC 杆发生拉伸变形1-3. 拉伸试件A 、B 两点的距离l 称为标距，在拉力作用下，用引伸仪量出两点距离的增量为Δl =5×10-2mm 。

若l 的原长为l =10cm ，试求A 、B 两点间的平均应变。

解：平均应变为42105100105Δ--⨯=⨯==l l m ε1-4. 图示三角形薄板因受外力而变形。

角点B 垂直向上的位移为0.03mm ，但AB和BC 仍保持为直线。

试求沿OB 的平均应变，并求AB 、BC 两边在B 点夹角的变化。

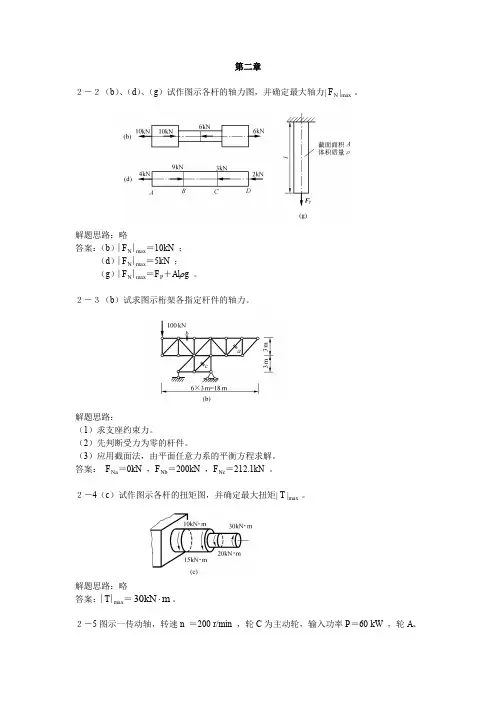
解：（1） 求OB 方向的平均线应变n4105.212003.0Δ120-⨯=====l l mmOA OB m ε （2）求AB 与BC 两边的角应变4105.2'22-⨯=-=OB AO arctg πγ2-1. 试求图示各杆1-1、2-2、3-3截面的轴力， 并作轴力图。

解: (a)（1）求约束反力kNR R X 500203040 0==-++-=∑（2）求截面1-1的轴力kNN NR X 500011==+-=∑（3）求截面2-2的轴力kNN NR X 10040 022==++-=∑（4）求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑（5）画轴力图(b)（1）求截面1-1的轴力01=N（2）求截面2-2的轴力 PN4022==（3）求截面3-3的轴力PN P P NX 304 033==-+=∑（4）画轴力图2-2. 作用图示零件上的拉力P=38kN ，试问零件内最大拉应力发生于哪个横截面上？并求其值。

材料力学第2版 课后习题答案 第3章 剪切实用计算

材料力学第2版 课后习题答案 第3章 剪切实用计算

P 30 × 10 3 l≥ = = 8.33cm b[τ ] 24 × 10 −3 × 40 × 10 6
l≥
2P 2 × 30 × 10 3 = = 12.7cm h σ iy 10 × 10 −3 × 90 × 10 6
[ ]
取 l = 127 mm 3-8 销钉式安全联轴器如图所示．允许传递扭矩Mn=300N.m。销钉材料的剪切强度 极限τb＝360 MPa，轴的直径D＝30mm。试确定销订的直径d。 解:
推进轴，其凸缘法兰承 小宽度 b=50mm ，材料 j]=22.5Mpa 。试校合其
3-6 某拖轮的螺旋桨 受总推力P=250KN，凸缘最 为 45 号钢，许用剪应力 [ τ 剪切强度。
解
τ =
P 250 × 10 3 = = 3.979 MPa < [τ ] 2πrb π × 0.4 × 0.05
习
题
3-1 夹剪的尺寸如图示，销子C的直径d＝0.5 cm，作用力 P=200 N，在剪直径与用 子直径相同的铜丝A时 ， 若 a＝2cm，b＝15cm． 试求铜丝与销子横截面上的平均剪进力τ。
解:
P × b = QA × a QA = τA = Pb 200 = × 15 = 1500 N a 2
3-2 图示摇臂，试确定其轴销 B 的直径 d 。已知用材料的许用应力 [ τ j]=100Mpa, [σjy]=240Mpa。
解:
74
∑MB = 0
P ⋅ cos 45� × 0.6 = 50 × 0.4
P = 47.14 KN
RB = 37.27 KN τ = R ≤ [τ ] 2 d2
π 4
2×3 2 6 πd [τ ] = π × 26 2 × 100 = 318.6 KN 4 4

材料力学性能-第2版课后习题答案

材料力学性能-第2版课后习题答案

第一章 单向静拉伸力学性能1、 解释下列名词。

1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4．包申格效应：金属材料经过预先加载产生少量塑性变形,卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面.6．塑性:金属材料断裂前发生不可逆永久（塑性)变形的能力。

韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b 的台阶.8。

河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时，便成为河流花样。

是解理台阶的一种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内,可以是韧性断裂，也可以是脆性断裂.沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂.11。

韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变12.弹性不完整性：理想的弹性体是不存在的，多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。

弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等2、 说明下列力学性能指标的意义。

答：E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 【P15】3、 金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标?答：主要决定于原子本性和晶格类型。

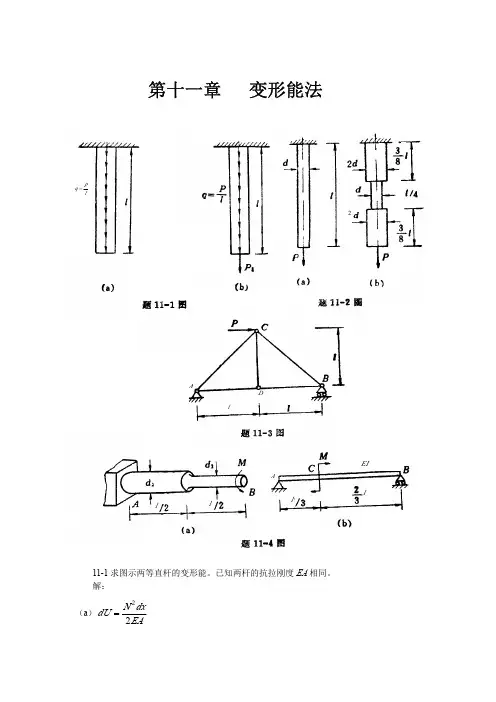
材料力学第2版 课后习题答案 第12章 变形能法

材料力学第2版 课后习题答案 第12章 变形能法

q2 4 ⎞ 2 2 3 ⎜ P x + qPx + x ⎟ ∫0 ⎜ ⎟dx 4 ⎝ ⎠
l⎛
δB =
∂U 1 = ∂P 2 EJ
⎛ 2 3 ql 2 ⎞ Pl 3 ql 4 ⎜ Pl + ⎟= ⎜3 ⎟ 3EJ + 8 EJ 4 ⎝ ⎠
11-6 试求下列图示各梁 A 点的挠度和截面 B 的转角，已知截面抗弯刚度 EI。
L
⎡
⎛L
⎞
⎤
5PL3 96 EJ
11-8 外伸梁的两支座均为弹性支座，弹簧的刚度（引起单位变形所需的力）分别为 k1 和 k2，已知梁的抗弯刚度 EI，试求外伸端 A 的铅直位移。 解：先求设两支座为非弹性支承时，A 端的铅直位移 δ A1 。
∑MB = 0
⎛ b⎞ y c = P ⎜1 + ⎟ ⎝ a⎠
第十一章
变形能法
q=
P l
2
A D l
EI
A
l
l
l
l
11-1 求图示两等直杆的变形能。已知两杆的抗拉刚度 EA 相同。 解：
N 2 dx （a） dU = 2 EA
N = qx =
l
P x t P2 x2 P 2l dx = 0 2 EAl 2 6 EA
l
U = ∫ dU = ∫
0
(b)
x N = P (1 + ) l x⎞ P ⎜1 + ⎟ l 7 P 2l l⎠ ⎝ U =∫ dx = 0 2 EA 6 EA
(
)
=
71qa 4 24 EJ
求 θB
M � ( x1 ) = −1 M � ( x2 ) = 0 θB =
⎤ 1 ⎡ a⎛ 5q 2 1 2 ⎞ ⎜ 2qax1 − a − qx1 ⎟(− 1)dx1 ⎥ ⎢ ∫ 0 EJ ⎣ ⎝ 2 2 ⎠ ⎦ 3 2 1 ⎛5 3 q a a ⎞ ⎜ qa + ⋅ ⎟ = − 2 qa ⋅ ⎟ EJ ⎜ 2 2 3 2 ⎝ ⎠ =−

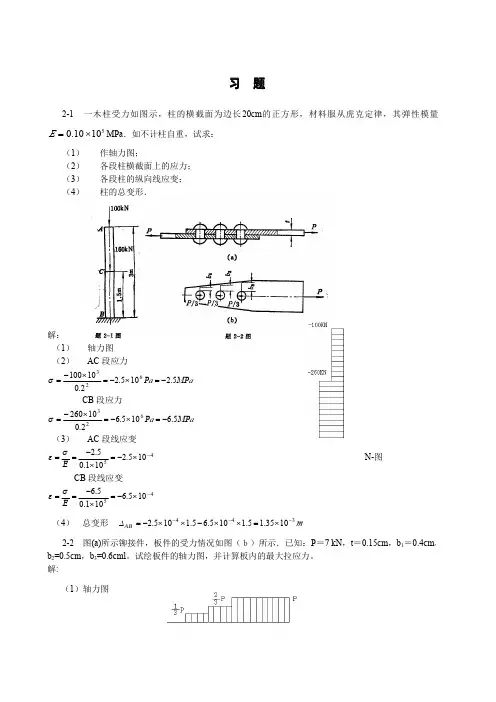
材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩

材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩

习题2-1一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量MPa ．如不计柱自重，试求：51010.0×=E （1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形．解：（1）轴力图（2）AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=（3）AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε（4）总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。

试绘板件的轴力图，并计算板内的最大拉应力。

解:（2）aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为１cm 的圆杆，在拉力P ＝10kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为＝30o 的斜截面上的正应力与剪应力。

α解:（1）最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−（2）界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。

材料力学II考试常考题及参考答案(2019年6月)

材料力学II考试常考题及参考答案(2019年6月)

材料力学II考试常考题及参考答案（2019年6月）工程力学一、填空题：1.受力后几何形状和尺寸均保持不变的物体称为。

2.构件抵抗的能力称为强度。

3.圆轴扭转时，横截面上各点的切应力与其到圆心的距离成比。

4.梁上作用着均布载荷，该段梁上的弯矩图为。

5.偏心压缩为的组合变形。

6.柔索的约束反力沿离开物体。

7.构件保持的能力称为稳定性。

8.力对轴之矩在情况下为零。

9.梁的中性层与横截面的交线称为。

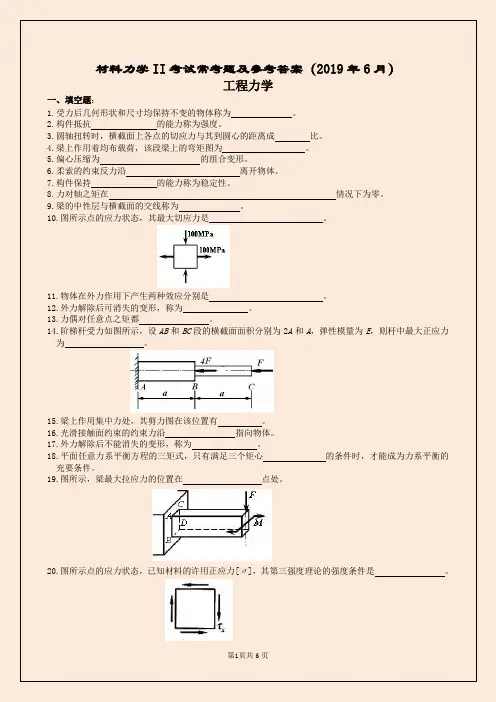
10.图所示点的应力状态，其最大切应力是。

11.物体在外力作用下产生两种效应分别是。

12.外力解除后可消失的变形，称为。

13.力偶对任意点之矩都。

14.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则杆中最大正应力为。

15.梁上作用集中力处，其剪力图在该位置有。

16.光滑接触面约束的约束力沿指向物体。

17.外力解除后不能消失的变形，称为。

18.平面任意力系平衡方程的三矩式，只有满足三个矩心的条件时，才能成为力系平衡的充要条件。

19.图所示，梁最大拉应力的位置在点处。

20.图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是。

21.物体相对于地球处于静止或匀速直线运动状态，称为。

22.在截面突变的位置存在集中现象。

23.梁上作用集中力偶位置处，其弯矩图在该位置有。

24.图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是。

25.临界应力的欧拉公式只适用于杆。

26.只受两个力作用而处于平衡状态的构件，称为。

27.作用力与反作用力的关系是。

28.平面任意力系向一点简化的结果的三种情形是。

29.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则截面C的位移为。

30.若一段梁上作用着均布载荷，则这段梁上的剪力图为。

二、计算题：1.梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m，M=10kN·m，求A、B、C处的约束力。

华南理工大学 材料力学 习题答案——第二版

华南理工大学 材料力学 习题答案——第二版

解题思路： （1）取滑轮为研究对象， ，由平面汇交力系的平衡方程求出杆 AB 的受力。 （2）查附录中的型钢表得杆 AB 的横截面积（注：两根角钢） 。 （3）由式（3－15）校核杆 AB 的强度条件。 答案：AB ＝74MPa 3－14 一结构受力如图所示，杆件 AB、AD 均由两根等边角钢组成。已知材料的许用应力 ＝170MPa，试选择杆 AB、AD 的角钢型号。
（m）FSmax＝5qa/3 ，Mmax＝25qa2/18 。 2－11（b）试用叠加法绘出图示梁的弯矩图。
解题思路：略 答案：MDA＝0；MBD＝MBC＝Fpa（上拉） 。 2－14 图示起重机横梁 AB 承受的最大吊重 FP＝12kN，试绘出横梁 AB 的内力图。
解题思路： （1）分析 AB 梁的受力，知 AB 梁发生轴向压缩和弯曲的组合变形。 （2）将外力分解为与杆轴重合的分量和与杆轴垂直的分量。 （3）由与杆轴重合的外力分量作出轴力图。 （4）由与杆轴垂直的外力分量作出弯矩图。 答案：MCBmax＝12kN.m，FNAC＝FNCA＝24kN 第三章 3－1 图示圆截面阶梯杆，承受轴向荷载 F1＝50kN 与 F2 的作用，AB 与 BC 段的直径分别为 d1＝20mm 与 d2＝30mm，如欲使 AB 与 BC 段横截面上的正应力相同，试求荷载 F2 之 值。
第二章 ２－２（b） 、 （d） 、 （g）试作图示各杆的轴力图，并确定最大轴力 FN max 。
解题思路：略 答案： （b）FNmax＝10kN ； （d）FNmax＝5kN ； （g）FNmax＝FP＋Alg 。 ２－３（b）试求图示桁架各指定杆件的轴力。
解题思路： （1）求支座约束力。 （2）先判断受力为零的杆件。 （3）应用截面法，由平面任意力系的平衡方程求解。 答案： FNa＝0kN ，FNb＝200kN ，FNc＝212.1kN 。 ２－4（c）试作图示各杆的扭矩图，并确定最大扭矩 T max 。

材料力学II习题解答 最终版

材料力学II习题解答 最终版

显然，B’C’段内的切应力分布和BC段的切应力分布相对于z 轴对称，方向相同，因此切应力的合力必大小相等，方向 相同，（题12.8图（c））
材料力学（II ）Mechanics of Materials 上海电力学院
材料力学（II ）Mechanics of Materials 上海电力学院
cc截面与B截面之间的面积（题12.8图（b））对z轴 的面矩为
b1 0
τ1δ1dξ
=
ξ F b1 Sy b1 −ξ
0
2Iz
δ1dξ
= FSyb13δ1
12Iz
根据合力矩定理，合力对一点之矩，等于其分力对同一点之
矩的代数和，可以证明
为 和 F S y
F S1
F S2
的合力。如
对B点取矩，水平方向剪应力的合力和剪力对B点之矩为零，
故有
FS y e = FS1 h
从上上式求得弯曲中心位置
⎤ ⎥ ⎦
=
24 bh2
Fl
=
24 × 6 × 103 × 1.25 75 × 10 −3 × 150 2 × 10 −6
Pa
= 107 M P a (拉 )
材料力学（II ）Mechanics of Materials 上海电力学院
B点的坐标为
yOB
=
h 3
zOB
=
−
b 3
带入广义弯曲应力公式，得
的壁厚 δ为常量，且壁厚及开口切缝都很小。
解: 如图（b）所示。开口处B面与bb截面间的面积 对在z轴的面距为
S
* z
=
(ξ δ
)ξ
2
=
δξ 2
2
⎛ ⎜⎝
0

第二版《材料力学》完整习题解答_(华中科大版_倪樵主编)

第二版《材料力学》完整习题解答_(华中科大版_倪樵主编)
dx

g
2
1
x
l2
l 2


0
因此
max

l

3 4
g
此处轴向变形为 l l gl2 3 2ln 2 0.403 gl2
4E
E
2-8
C
B
30 45
A
1m
0.8 m
F
A
45
l2 30
l1
R
P A
Q
对A点列平衡方程：
有两个铆钉，每个铆钉所受剪切力为:
Fs 2
则铆钉剪切面上的切应力为:
Fs / 2 59.3 MPa d2 /4
2-25
C FC

DF
1.5 m
1.5 m
F
2.1 mm 时 l f 所以B端不受约束，此时
FC F FB 0 F 200 kN 80 MPa

0
sin 2 45

50
MPa
各截面受力如图：
b
F
F
h
2-5
n
F
a
粘接面
2-6
1
2
l
3
C
A
l2
F
B
l2
A l1
A
角度为a的斜截面上的正应力和切应力分别为：
F
0 cos2 a
要使 2


1 2

0
sin
2a
则有
0
cos2 a

2
1 2

0
sin 2a

2 0
30 cm

《材料力学》第二章课后习题及参考答案

《材料力学》第二章课后习题及参考答案
简答题2答案
在材料力学中，应力和应变是描述材料受力状态的基本物理量。应力表示单位面积上的 力，而应变则表示材料的变形程度。
简答题3答案
弹性力学和塑性力学是材料力学的重要分支。弹性力学主要研究材料在弹性范围内的应 力、应变和位移，而塑性力学则研究材料在塑性变形阶段的力学行为。
选择题答案
80%
选择题1答案
选择题3解析
这道题考察了学生对材料力学中 弯曲应力的理解，学生需要理解 弯曲应力的概念和计算方法，并 能够根据实际情况进行选择和应 用。
计算题解析
01
计算题1解析
这道题主要考察了学生对材料力学中拉压杆的计算能力，学生需要掌握
拉压杆的应力、应变计算方法，并能够根据实际情况进行选择和应用。
02
计算题2解析
计算题2答案
根据题意，先求出梁的剪力和弯矩，然后根据剪力和弯矩的关系 求出梁的位移分布，最后根据位移和应力的关系求出应力分布。
03
习题解析Biblioteka 简答题解析简答题1解析这道题考查了学生对材料力学 基本概念的理解，需要明确应 力和应变的概念及关系，并能 够解释在材料力学中如何应用 。
简答题2解析
这道题主要考察了学生对材料 力学中弹性模量的理解，以及 如何利用弹性模量进行相关计 算。学生需要理解弹性模量的 物理意义，掌握其计算方法。
C. 材料力学的任务之一是研究材 料的各种力学性能，包括强度、 刚度和稳定性等。
100%
选择题2答案
D. 在材料力学中，应力和应变是 描述材料受力状态的基本物理量 。
80%
选择题3答案
B. 材料力学主要研究材料的力学 性能和内部结构的关系，包括弹 性、塑性和韧性等。
计算题答案

《材料力学》Ⅱ(第四版)答案

《材料力学》Ⅱ(第四版)答案

P u \:PN1PD[ u TO 0$ FRV FRV PD[PD[u M 00]PN1 $ VLQ VLQ PD[PD[u M 00\PN1PD[PD[ u uu u \\]]$:0:0V 03D \$%PO\¸¸¹·¨¨©§ ¸¸¹·¨¨©§]\\]\],T ,T (O Z Z Z¸¸¹·¨¨©§u u ¸¸¹·¨¨©§u u u uuPuu uu uuPPhPPhPP%]]:0PD[PD[V \\:0PD[PD[VPD[\%\%%Z Z Z Z &%]&$]&$&%\&\&\%O (,O)(,O )O Z Z u uTPu u u u u K Z ,]]u u u u u u u u u u u u u \%Z P u Pu u u u uE Z ,\\\$%]%(,O )ZPu u u u u u u)PD[]0u:03D PN1PD[ uV =\U\³³1GG$$)$$VV³³GG$$$\($\(UU³³GG$$$\,$\,,(,(U³³GG$$$\($\(@>@>QQQQ[\\E(\K[\E(&&\[\[K$E[$[K EQ&&\$(\$(\$($(N1)*3DZ(UV\(]³³GG$$$\($\(UU]6]]6(6(@>@>uuuuuuuu KKKPP³³³³G G G G $$$$,(,($\($\($\$\0UUU VV¦6 6 \)\)0$,\\PPH$DVLQ U $6]$WDD D VLQ VLQ VLQ 6 6 6UW )W U $U $)W ,6)DD VLQ U H |$TD$DD D D D D FRV VLQ FRV VLQ UH\PPP\PD[uuuu uG G 0:0VVHH$VV))%VVV$)&&VVVVVVV$)$)$)&&$)%V V ¦ D)D )D )0%$FRVV X D V $)VV VFRV V V D V $)FRVV V V V)))) V V D V V V)X)PPPP'GVVVXuuuu³G7G WUWUPN1@>VVKXuuu³G'7'G WUWUXV777VVVVVVU5UUU75UU³³WWUUWUUWUW75UW75UV::EFWFVGVLQGTG M UU$\666:GGGGGU UUUUGGGGGGU UUUUUVEK EK ::03DVV PPu u \\\F W V\\\66: uPP @ > u u \P N1 V V X u u u :0VPPPP KE 03DVVD$X X0O T O )00%$XD OD O T D O )%X XD OD O T D O D O TDE(GO)(GO)G (O )($O )9LLL ¦u[G [)991DFO[T[[0dd³³O O[[0[[0(,9(,O TO TO T(,[TO[T[(,OO@>@GG>³³($O )[[0[[0(,9OO@G G >1DEHV %$[$&³³ HH HH H H V@>''''HDOO[$$&$&$&»»»¼º«««¬ªD%OO%%Y[$\$$%$%$%$%''H[$\$D D%''F$DD(,)O)9$\FG($O)(,O)9ww'O)OT)T+$')GGG(,D 0\0[[D[0D (,09D D0%%%G GHH HE9$'¿¾½¯®­³³9³³w wOO[[TO[TO [[TO[TO (,)9)$'(,TO$%%³³w wO O ))$\O )\O )(,[[)(,)9GG$' )))9 w wGG$TGG%TGG @>³³w w O O $\)\(,[[T[[TO)(,)9%,$%$%D&0&³³ O O \\)\\)(,9G G^ H ³G @ >O &[[O 0)O )`G @> [)O [O 0)O &³E@GG >DD[D)D \)\(,)9(,)D&T &&T &0FG@>GG^³³³ DDD [[D )\)D [)[`G @ >G G 9 $%'³³³w w D D D [[D )\)D [)[(,)9G@ >G G ^³³ DD\\))D [)[G G ³ DD )D )>G @[[+ $%'S9$%'$$$FFTw w$%0$%$%09T³³SG VLQ FRV G FRV VLQ TT T T T T )5*,5)5(,5S*,)5$%DDTTT VLQ $%TFRV($O )($O )9$&$&$%$%$))))$&$%+$'($)D )9)$%D'%9D%E³³ O O '[[T[;[(,[[[TO ;(,G G ' (,;O O T O ;(,O TO ;(,O;)O O [);O [0 w w ³³ O O $[O )O O [);O (,[[;[O )(, G @G 'O )O O );O (,O O ;O )O (,);)$)D 0$)D 0%I))D;;;E;³TO ;O;EE;;;³D[T[(,9;;9FED N1 N1 ;N1 N1 ;PN1 D ;0%PN1TE E ;D ;0&TD TDTDTD 016$%&TGO[[;[0ddwwww[0[;wwwwdd[7;7O[;[7O[;)[[;[0ddwwww;0[;O[;7O;7O;[7ddwwww³³@GG> O O[[;)[[;[[[;(,'³O3[O O;*,G(,*, SSO;O)O;(,*,O;)O;O;³G FRV VLQ VLQ T T T T (,)5 (,)5(,)5G VLQ $0$50)5(,TT T³E>FRVFRV TT T5;)50 @G@>(,)5 @(,)5G VLQFRVFRV T T T T '55)5(,;$\³FRV FRVFRVT T T (,)5TT T T G FRV VLQVLQ$;³G FRV T T T 5)5(,;$³(,)5FFRV T w w 5)³G FRV FRV T T T(,)5(,)5G VLQ FRV TT T '55)5(,;$\³G FRV TT T 5)5(,;$(,)5GVLQVLQ dd w w T T T T 55))5)5055T³³5$\55)5(,[[)[(,G VLQ VLQ T T T (,)5(,)5(,)5G FRV VLQ T T T '55)5(,;$[³G VLQGTT T³(,)5(,)5(,)5HG VLQ VLQ T T T '55)5(,$]³³³SGFRV FRV G FRV T TT T T *,)5(,)5@`^@w w w w ;7;0\³ $$$G @ VLQ FRV > T T '555(,;$[G VLQ VLQ T T T MT 5)5(,$³PPG *3D('O )7)O [7 w w³³ O O '(,[O )O (,[[)[(,G G '³³ OO[O )O *,[[)[SGG S S*,)O (,)O *,)O O O O (,)u u u uu u u uu u u u u u u u)*['[GG G G G G '' '*&*%*$*G 'G G 'G G 'G ' '*&*%*$*GGG GG 'O($O($)9L LL %%[DEO [OO [TO [0d dEO [[[0d d³O$[(,[0[0 GT ³ G O [(,T[[(,O [TO O O G @ > ³ (,TO (,TO(,TOFD$EO [[[0d d[O O [[[0O [Od d³O&[(,[0[0 GG ³ H G O [(,[[O 0³ O O [(,[O 0[O 0 H H G(,O 0(,O 0(,O 0 H H HFO [O[[0d dGD$O [T[[0d dO[O O [TO T[[0d dEO[[[0d dO[O O[O [[[0d d³G@>OO[(,O[O[TOT[(,TOP Pd d[[[[[0($F(,D$E%$ '&F&' & ' E) ) 1³³ DD [(,[)[[(,[)[G G (,)DF%&''EFGD'&)[[0+' '@G G > ³³ DD [D [D )[[)D (, (,)DG[0[0'T ³³³ D D D[[D )[)D [)[(, @G G G >(,)D&%)D [0&&F&%[0%$[0 [7EO[7 &&³ O[O TO *,S GS*,TO (,TOFVLQFRVT T T 5G VLQFRVFRV T T T T 55)5(,!S (,)5³FRV 5G )5(,$TTF))[[05[d dVLQ T T )50(,)5³³SG VLQ FRV G FRV VLQ TT T T T T T )5*,)5(,$ S*,)5(,)5$T$$G$DK$KO [0d d TE(,)O Z Z$%EF。

第二版《材料力学》习题解答

第二版《材料力学》习题解答

A =AR +RP
l2 cos 30
+ Ax
tan
30=1.367
mm
2-9
F A
l
y
y
f ky2
f
对A点列平衡方程：
l
Fy 0 : ky2dy F
0
k
3F l3
在y处截面的内力为：
N
பைடு நூலகம்
y
y 0
ky2dy
1 ky3= 3
F l3
y3
由胡克定律，在y截面的应变为：
E
N y
EA
F EAl3
0
sin
2a
则有
0
cos2 a
2
1 2
0
sin
2a
2 0 sin a
cos a
cosa 2 sin a
a =arctan0.5=arcsin 1 =arccos 2
5
5
对刚性杆AB列平衡方程：
N1 N3
N 2
Fy 0 : N3 0
Fx 0, M ( A) 0 :
A
F
B
N1 N2 F 2
MPa
a=45°时： 45
45
0 1 2
cos2 0 sin
45
2
50
45
MPa 50
MPa
a=-45°时： 45
45
1 2
0 cos2 45 50 MPa 0 sin 2 45 50
MPa
a=135°时： 135
135
0 cos2 135 50 MPa
1 2
0
sin
2
y3
地桩总的缩短量为：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

轴y1、z2分别为CBD和BDA的对称轴，故
，
则
I y0 z0
=
I y1z1
− abA =
h× 6
h × bh 62
=
b2h2 72
材料力学（II ）Mechanics of Materials 上海电力学院
最大弯矩发生在悬臂梁根部截面上 M z = Fl
A点的坐标为
yOA
=
−
2 3
h
zOA
=
−
b 3
( ) Iz = Iz1 + Iz2
=1 12
δ1b13 + δ2b23
翼缘①内的切应力
τ1
=
FS S z*
δ Iz
=
F S y δ 1ξ
⎛ ⎜⎝
b1 2
σ 1Iz
−
ξ
2
⎞ ⎟⎠
(0
≤
ξ
≤ b1 )
材料力学（II ）Mechanics of Materials 上海电力学院
∫ ∫ ∫ ( ) ( ) FS1 = τ1dA = A
( ) σ B = M x
I z yO zO OC − I yO yOC
I I − I yO zO
2 yO zO
=
Fl
⎡ b2h2 ⎢⎣ 72
⎛ ⎜⎝
−
hb3 ⎛ h3b
36
⎜ ⎝
36
b 3
⎞ ⎟⎠
−
hb3 36
⎛ ⎜⎝
h 3
⎞ ⎟ ⎠
−
⎛ ⎜ ⎝
b2h2 72
⎞2 ⎟ ⎠
⎞⎤ ⎟⎠ ⎥⎦
=
−
24 bh2
Fl
=
−107MPa(压 )
C点的坐标为
yOC
=
h 3
zOC
=
2b 3
材料力学（II ）Mechanics of Materials 上海电力学院
带入广义弯曲应力公式，得
( ) σ C = M z
I z yO zO OC − I yO yOC
I I − I yO zO
2 yO zO
=
Fl
⎡ ⎢⎣
b2h2 72
材料力学（II ）Mechanics of Materials 上海电力学院
课后作业答案讲解
Chapter 12
弯曲的几个补充问题
Chapter 13
能量方法
Chapter 14
超静定结构
Chapter 15
平面曲杆
材料力学（II ）Mechanics of Materials 上海电力学院
Chapter 12
M1 EI
w4
− 2w3
−
w2
=
⎛ ⎜⎝
l ⎞2 6 ⎟⎠
M3 2EI
M3
=
Fl 4
E3I3 = 2EI
h= l 6
w3
−
2w2
−
w1
=
⎛ ⎜⎝
l 6
⎞2 ⎟⎠
M2 2EI
材料力学（II ）Mechanics of Materials 上海电力学院
补充条件： w0 = 0 w1 = w5 w2 = w4
b1 0
τ1δ1dξ
=
ξ F b1 Sy b1 −ξ
0
2Iz
δ1dξ
= FSyb13δ1
12Iz
根据合力矩定理，合力对一点之矩，等于其分力对同一点之
矩的代数和，可以证明
为 和 F S y
F S1
F S2
的合力。如
对B点取矩，水平方向剪应力的合力和剪力对B点之矩为零，
故有
FS y e = FS1 h
从上上式求得弯曲中心位置
材料力学（II ）Mechanics of Materials 上海电力学院
AC断任一截面上的弯矩方程为
M ( x1 )
=
FRA x1
−
1 2
qx12
−
M
A
CB断任一截面上的弯矩方程为
M (x2 ) = − F0 x2
由平衡条件可计算出
FRA = F0 + aq
M
A
=
F0l
+
1 2
qa2
应用卡氏定理，B截面的挠度
⎤ ⎥ ⎦
=
24 bh2
Fl
=
24 × 6 × 103 × 1.25 75 × 10 −3 × 150 2 × 10 −6
Pa
= 107 M P a (拉 )
材料力学（II ）Mechanics of Materials 上海电力学院
B点的坐标为
yOB
=
h 3
zOB
=
−
b 3
带入广义弯曲应力公式，得
——弯曲的几个补充问题
12--3 12--6
12--7 12--8
12--16 12--17
材料力学（II ）Mechanics of Materials 上海电力学院
12.3作用于图示悬臂梁上的载荷为：在水平平面内F1=800N， 在垂直平面内，F2=1650N。木材的许用应力 [σ] =10 MPa 。若矩 形截面 h = 2 ，试确定其尺寸。
带入广义弯曲应力公式，得
( ) σ A
=
Mz
I yO zO zOA − I yO yOA
I I − I yO zO
2 yO xO
=
Fl
⎡ b2h2
⎢ ⎣
72
⎛ ⎜⎝
−
b 3
⎞ ⎟⎠
−
hb3 36
⎛ ⎜⎝
−
2 3
hb3 36
⎛ ⎜ ⎝
h 3b 36
⎞ ⎟ ⎠
−
⎛ ⎜ ⎝
b2h2 72
⎞2 ⎟ ⎠
h
⎞ ⎟⎠
材料力学（II ）Mechanics of Materials 上海电力学院
解: 直角三角形截面的形心为截面对形心轴的惯性矩和
惯性积
I z0
=
Iz
− a2A
=
1 bh3 12
−
⎛ ⎜⎝
h 3
⎞2 ⎟⎠
⎛ ⎜⎝
bh 2
⎞ ⎟⎠
=
bh3 36
同理
Iy 0
=
hb3 36
取斜边中点D建立y1、z2坐标系，如图12.6（b）所示。
解: 将简支梁分成六个相等的间隔，在梁上确定0、1、2、 3、4、5、6点，由题12.17图可得
材料力学（II ）Mechanics of Materials 上海电力学院
M1
=
Fl 12
E1I1 = EI
M2
=
Fl 6
E2 I2 = 2EI
带入差分方程
w2
−
2w1
−
w0
=
⎛ ⎜⎝
l 6
⎞2 ⎟⎠
Wy
Wz
bh 2
hb 2
将 h b = 2 带入上式得
h
≥
σ ]
z
=
3
1
2
×
1.65
×
103 + 24 10 ×106
×
1
.6
×
103
m
= 180mm
截面尺寸为 b=90mm, h=180mm
材料力学（II ）Mechanics of Materials 上海电力学院
12.6悬臂梁的横截面为直角三角形，h=150mm,b=75mm。自 有端的集中力F=6kN，且通过截面形心并平行于三角形的竖 直边。若不计杆件的扭转变形，试求固定端A，B，C应力。 设跨度 l = 1.25m
×
Fl2 16EI
=
F Δc
由上式得
Δc = M cl2 16EI
材料力学（II ）Mechanics of Materials 上海电力学院
13.7（a）试用图示各粱的截面B的挠度和转角。EI为常数。 解：如题图13.7（a）所示。因B点无集中应力作用，故欲 求该处挠度须在B点加一虚力F0=0，如图13.7（a）所示。
=
1 2
FRA x 2
−
M
Ax
−
q 6
⎛ ⎜⎝
x
−
l 4
⎞3 ⎟⎠
+
C
③
EIω
=
1 6
FRA x3
−
1 2
M
Ax2
−
q 24
⎛ ⎜⎝
x
−
l 4
⎞4 ⎟⎠
+
Cx
+
D
④
利用便捷条件确定积分常数
初始条件：
w = 0 w' = 0 w = 0
x=0
x=0
x=l
⑤
材料力学（II ）Mechanics of Materials 上海电力学院
⎛ ⎜⎝
2b 3
⎞ ⎟⎠
−
hb3 36
⎛ ⎜⎝
h 3
hb3 36
⎛ ⎜ ⎝
h3b 36
⎞ ⎟ ⎠
−
⎛ ⎜ ⎝
b2h2 72
⎞2 ⎟ ⎠
⎞⎤ ⎟⎠⎥⎦
=
0
因O点、C点应力为零，所以OC连线为中性轴。
材料力学（II ）Mechanics of Materials 上海电力学院 12.7试确定图示薄壁截面的弯曲中心A的位置。
显然，B’C’段内的切应力分布和BC段的切应力分布相对于z 轴对称，方向相同，因此切应力的合力必大小相等，方向 相同，（题12.8图（c））
材料力学（II ）Mechanics of Materials 上海电力学院