成都市东湖中学八上数学直角坐标系导学案

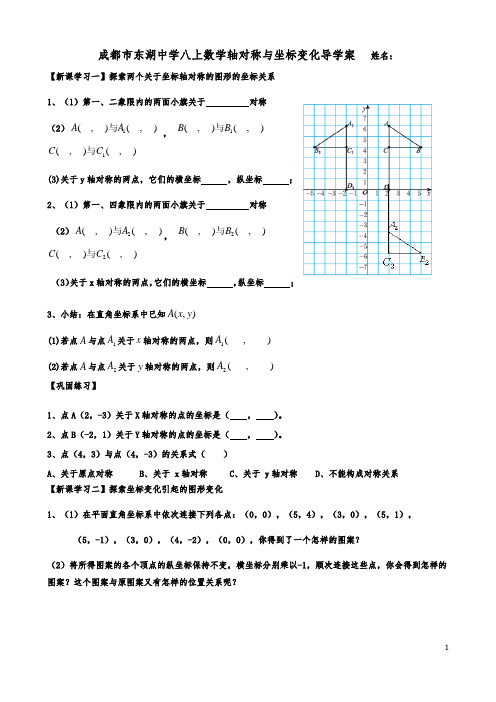
成都市东湖中学八上数学轴对称与坐标变化导学案 姓名：【新课学习一】探索两个关于坐标轴对称的图形的坐标关系1、（1）第一、二象限内的两面小旗关于 对称（2）1(__,__)(__,__)A A 与 ， 1(__,__)(__,__)B B 与1(__,__)(__,__)C C 与(3)关于y 轴对称的两点，它们的横坐标 ，纵坐标 ；2、（1）第一、四象限内的两面小旗关于 对称（2）2(__,__)(__,__)A A 与， 2(__,__)(__,__)B B 与2(__,__)(__,__)C C 与（3）关于x 轴对称的两点，它们的横坐标 ，纵坐标 ；3、小结：在直角坐标系中已知),(y x A(1)若点A 与点1A 关于x 轴对称的两点，则____)(___,1A(2)若点A 与点2A 关于y 轴对称的两点，则____)(___,2A【巩固练习】1、点A （2，-3）关于X 轴对称的点的坐标是（ ， ）。

2、点B （-2，1）关于Y 轴对称的点的坐标是（ ， ）。

3、点（4，3）与点（4，-3）的关系式（ ）A 、关于原点对称B 、关于 x 轴对称C 、关于 y 轴对称D 、不能构成对称关系【新课学习二】探索坐标变化引起的图形变化1、（1）在平面直角坐标系中依次连接下列各点：（0，0），（5，4），（3，0），（5，1），（5，-1），（3，0），（4，-2），（0，0），你得到了一个怎样的图案？（2）将所得图案的各个顶点的纵坐标保持不变，横坐标分别乘以-1，顺次连接这些点，你会得到怎样的图案？这个图案与原图案又有怎样的位置关系呢？所得的点，你会得到怎样的图案？这个图案与原图案有怎样的位置关系呢？【巩固练习】1．完成下表：2 3．如图，利用关于坐标轴对称的点的坐标的特点，分别作出与△ABC 关于x 轴和y 轴对称的图形４.如图，在平面直角坐标系中，已知点A（0，3），B（2，4），C（4，0），D（2，﹣3），E（0，﹣4）．写出D，C，B关于y轴对称点F，G，H的坐标，并画出F，G，H点．顺次而平滑地连接A，B，C，D，E，F，G，H，A各点．观察你画出的图形说明它具有怎样的性质，它象我们熟知的什么图形？５．将下图中的点（2，1），（5，1），（2，5）做如下变化：（1）纵坐标不变，横坐标分别加2．（2）横坐标不变，纵坐标分别加1．（3）纵坐标不变，横坐标分别变为原来的2倍．（4）横坐标不变，纵坐标分别变为原来的2倍．（5）纵坐标不变，横坐标分别乘以-1．（6）横坐标不变，纵坐标分别乘以-1．（7）纵坐标、横都分别乘以-1，观察变化后的三角形与原三角形有什么变化？６、如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．实验与探究：(1)由图观察易知A（0，2）关于直线l的对称点A'的坐标为（2，0），请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点B'、C'的位置，并写出他们的坐标:B'、C'；归纳与发现：(2)结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P'的坐标为（不必证明）；运用与拓广：(3)已知两点D(1,-3)、E(-1,-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．。

八年级数学系上册第三章平面直角坐标系（3）导学案学校： 班级： 姓名： 学习过程活动一：建立平面直角坐标系，描述图形1.如图，矩形ABCD 的长与宽分别是6，4，建立适当的直角坐标系，并写出各个顶点的坐标。

交流。

反思2.在上面的问题中，你还可以怎样建立直角坐标系？与同伴交流.3.对比不同的建立坐标系的方法,你更喜欢哪一种?谈谈你的看法.运用。

巩固4. 如图，建立两个不同的直角坐标系，在各个直角坐标系中，分别写出八角星 8 个角的顶点的坐标，并比较同一顶点在两个坐标系中的坐标．5.对于边长为4的正△ABC ，建立适当的直角坐标系，写出各个顶点的坐标.活动2：根据坐标复原图形在一次“寻宝”游戏中，寻宝人已经找到了坐标为（3，2）和（3，-2）的两个标志物A,B ，并且知道藏宝地点的坐标（4，4），除此外不知道其他信息。

如何确定直角坐标系找到“宝藏”？活动3：反思总结关于建立平面直角坐标系，你有哪些经验？活动4：自主反馈1.如图，建立适当的直角坐标系，并写出这个四角星的八个顶点的坐标。

2（2，－5）4，－2）所在的位置的坐标为 。

课堂检测1．点P (2m -1,3)在第二象限，则m 的取值范围是（ ）A ．12m >B ．12m ≥C ．21<mD ．12m ≤ 2．点M (-3,4)关于原点的对称点为N ，则MN =3．已知直角坐标系中的A (m ,3)和B (4,n )两点，根据下列条件求出m 、n 的值．(1)A 、B 两点关于y 轴对称；(2)A 、B 两点关于x 轴对称；(3)A 、B 两点关于原点O 对称；(4)AB ∥y 轴；(5)A 、B 两点在第一、三象限两条坐标轴夹角的平分线上．4△ABC 5作业习题。

3.2 平面直角坐标系（1）学习目标：1、理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念，并能画出平面直角坐标系。

2、能在给定的直角坐标系中，由点的位置写出它的坐标。

3、通过画坐标系，由点找坐标等过程，发展学生的数形结合意识、合作交流意识。

预习案课前导学：阅读课本P58~P60，完成下列内容：1.平面直角坐标系定义：在平面内，两条____________且有公共_________的数轴组成平面直角坐标系，简称_________________。

通常，两条数轴分别置于水平位置与铅直位置，取________ __和_________的方向分别为两条数轴的正方向，水平的数轴叫做__ ___或_______，铅直的数轴叫做_______或_______，两者统称为_______，它们的公共原点O称为直角坐标系的_______。

2.如图，对于平面内任意一点P，过点P分别向x 轴，y轴作_______，垂足在x轴、y轴上对应的数a，b 分别叫做点P的_______、_______，有序数对（a，b）叫做点P的_______。

3.如右图1－5－1，两条坐标轴把平面分成四个部分：右上部分叫做第一象限，其他三个部分按_______方向依次叫做第_______象限和第_______象限和第_______象限。

尝试练习：1.A（2，3）的横坐标是_____，纵坐标是_____，点A在第_____象限；2.B（-2，3）的横坐标是_____，纵坐标是_____，点B在第_____象限；3.C（-2，-3）的横坐标是_____，纵坐标是_____，点C在第_____象限；4.D（2，-3）的横坐标是_____，纵坐标是_____，点D在第象限；5.如果点E的横坐标为0，那么点E在______轴上；6.如果点F的纵坐标为0，那么点F在_____轴上.学习案知识点拨：1.（1）如果用（0，0）表示科技大楼的位置，用（5，7）表示中心广场的位置，那么钟楼的位置如何表示？（2，5）表示哪个地点的位置？（5，2）呢？（2）如果小明和他的朋友在中心广场，并以中心广场为原点，以图中小正方形的边长为单位长度，建立平面直角坐标系。

直角坐标系教学内容及其分析（一）教学内容：一、平面直角坐标系和横轴、纵轴、原点、坐标的概念二、依照坐标确信图形的位置，依照图形确信各点的坐标。

（二）教学内容分析：一、本节课要学习的内容平面直角坐标系和横轴、纵轴、原点、坐标的概念，其核心是画出直角坐标系，明白得各个部份的名称，本知识点是为后面学习由点的位置写出它的坐标，依照坐标描出点的位置打下基础，是本节中学习的重要基础内容。

二、依照坐标确信图形的位置，依照图形确信各点的坐标。

其核心是在给定的直角坐标系中，由点的位置写出它的坐标；依照坐标描出点的位置。

关键是根据题中的已知条件描点，明白得横轴和纵轴的概念。

为以后学习坐标转变与图形转变之间的关系打好基础。

也是本节的重点。

二、目标及其解析（一）、目标定位：明白得平面直角坐标系和横轴、纵轴、原点、坐标等概念；能在给定的直角坐标系中，由点的位置写出它的坐标。

（二）目标解析：平面直角坐标系是在平面中确信点点的位置的要紧载体，它是后面研究各类函数的重要基础，因此要明白得概念，并准确把握。

坐标是一对有序实数对，前后不能倒置。

三、问题诊断与分析在本节课的教学中，学生可能碰到的问题是点的坐标、与点到坐标轴的距离，横纵坐标混乱，产生这一问题的缘故是忽略了点的坐标是是一对有序实数对。

要解决这一问题，其中关键对本概念的明白得。

四、教学支持条件分析五、教学进程一、引入新课同窗们，你们喜爱旅行吗？假设你到了某一个城市旅行，那么你应如何确信旅行景点的位置呢？下面给出一张某市旅行景点的示用意，依照讲义示用意（图5－6），回答以下问题：（1）你是如何确信各个景点位置的？（2）“大成殿”在“中心广场”南、西各多少个格？“碑林”在“中心广场”北、东各多少个格？（3）若是以“中心广场”为原点作两条相互垂直的数轴，别离取向右、向上的方向为数轴的正方向，一个方格的边长看做一个单位长度，那么你能表示“碑林”的位置吗？“大成殿”的位置呢？设计用意：以方格纸为背景，引出平面直角坐标系。

成都市东湖中学八上数学《平面直角坐标系》复习导学1、 在平面内，两条互相垂直且有公共原点的数轴组成了平面直角坐标系；2、 坐标平面上的任意一点P 的坐标，都和惟一的一对有序实数对（b a ,）一一对应；其中，a 为横坐标，b 为纵坐标坐标；3、x 轴上的点，纵坐标等于0；y 轴上的点，横坐标等于0；坐标轴上的点不属于任何象限；4、 四个象限的点的坐标具有如下特征：小结：（1）点P （y x ,）所在的象限 横、纵坐标x 、y 的取值的正负性；（2）点P （y x ,）所在的数轴横、纵坐标x 、y 中必有一数为零；5、 在平面直角坐标系中，已知点P ),(b a ，则（1） 点P 到x 轴的距离为b ； （2）点P 到y 轴的距离为a ；（3） 点P 到原点O 的距离为PO ＝22b a +6、 平行直线上的点的坐标特征：a) 在与x 轴平行的直线上， 所有点的纵坐标相等；点A 、B 的纵坐标都等于m ；b) 在与y 轴平行的直线上，所有点的横坐标相等；点C 、D 的横坐标都等于n ；7、 对称点的坐标特征：a) 点P ),(n m 关于x 轴的对称点为),(1n m P -， 即横坐标不变，纵坐标互为相反数；b) 点P ),(n m 关于y 轴的对称点为),(2n m P -， 即纵坐标不变，横坐标互为相反数；点P ),(n m 关于原点的对称点为),(3n m P --，即横、纵坐标都互为相反数；8、 两条坐标轴夹角平分线上的点的坐标的特征：a) 若点P （n m ,）在第一、三象限的角平分线上，则n m =，即横、纵坐标相等；b) 若点P （n m ,）在第二、四象限的角平分线上，则n m -=，即横、纵坐标互为相反数；在第一、三象限的角平分线上 在第二、四象限的角平分线上考点1：考点的坐标与象限的关系 知识解析：各个象限的点的坐标符号特征如下：（特别值得注意的是，坐标轴上的点不属于任何象限.）1、在平面直角坐标中，点M (－2，3)在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2、在平面直角坐标系中，点P (－2，2x ＋1)所在的象限是（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3、点P （m ，1）在第二象限内，则点Q （-m ，0）在（ ）A ．x 轴正半轴上B ．x 轴负半轴上C ．y 轴正半轴上D ．y 轴负半轴上4、若点P （a ，b ）在第四象限，则点M （b －a ，a －b ）在（ ）A. 第一象限B. 第二象限C. 第三象限D. 第四象限5、在平面直角坐标系中，点(12)A x x --，在第四象限，则实数x 的取值范围是 ．X6、对任意实数x ，点2(2)P x x x -，一定不在．．（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 7、如果a －b ＜0,且ab ＜0,那么点(a ，b)在( )A 、第一象限B 、第二象限C 、第三象限,D 、第四象限.考点2：点在坐标轴上的特点 x 轴上的点纵坐标为0, y 轴上的点横坐标为0.坐标原点（0，0）1、点P （m+3，m+1）在x 轴上，则P 点坐标为（ ）A ．（0，-2）B ．（2，0）C ．（4，0）D ．（0，-4）2、已知点P (m ，2m －1)在y 轴上，则P 点的坐标是 。

成都市东湖中学八上数学二元一次方程组与一次函数导学案 姓名：活动：⒈回顾交流，迁移知识⑴方程0=-y x 的解有多少个？写出其中的几个．⑵在直角坐标系中分别描出以这些解为坐标的点，（x 的值为横坐标、y 的值为纵坐标），你有什么发现吗？⑶在图象上任取一点，它的坐标适合方程0=-y x 吗？⑷以方程0=-y x 的解为坐标的所有点的全体叫做方程0=-y x 的图象（5）根据上面的探究想一想：方程0=-y x 的图像是什么结论：一般的：任何一个二元一次方程的图像都是一条直线；直线上的任何一个点都是对应二元一次方程的解【问题牵引】我们知道，每个二元一次方程都对应一条直线． 请你解出二元一次方程组35821x y x y +=⎧⎨-=⎩ 的解，并回答：1、画出这两个函数的图象2、由这两个函数的图像，你能得出这个二元一次方程组的解吗？二元一次方程组与两个直线的关系: 每个二元一次方程组都对应两条 ，从“数”的角度看，解方程组相当于考虑x 为何值时两个y 的值 ，；从“形”的角度看，解方程组相当于确定两条直线 的坐标． 训练：⒈请根据下列图像，说出它们是哪些方程组的解？这些解是什么？x⒉在直角坐标系中有两条直线：1l ：5953+=x y 和2l ：623+-=x y ，它们的交点为P ，1l 与x 轴交于点A ，2l 与x 轴交于点B ．⑴A 、B 两点的坐标；⑵写出直线1l 与2l 的交点P 的坐标； ⑶求PAB ∆的面积．检测:⒈如果直线63+=x y 与42-=x y 交点坐标为),(b a ，则x ay b =⎧⎨=⎩是方程组__的解（ ） A ．3624y x y x -=⎧⎨+=-⎩ B ．3624y x y x -=⎧⎨-=⎩ C ．3634x y x y -=⎧⎨-=⎩ D ． ⎩⎨⎧-=--=-4263y x y x⒉已知11+-=x y 和122--=x y ，当2->x 时21y y >；当2-<x 时21y y <，则直线11+-=x y 和直线122--=x y 的交点是（ ）A ．)3,2(-B ．)5,2(--C ．)2,3(-D ．)2,5(--⒊已知方程412+-=+x x 的解是1=x ，则直线12+=x y 与4+-=x y 的交点是（ ） A.)0,1( B ．)3,1( C ．)1,1(-- D ．)5,1(--⒋已知直线b ax y +=经过点)2,1(和)3,2(，则a =________，b =________．⒍直线12-=x y 与4+=x y 的交点是)9,5(，则当x _______时，直线12-=x y 上的点在直线4+=x y 上相应点的上方；当x_______时，直线12-=x y 上的点在直线4+=x y 上相应点的下方．7.直线63+=x y 与42-=x y 交点坐标为),(b a ，则x ay b =⎧⎨=⎩是方程组（ ）的解 。

成都市东湖中学八上数学——勾股定理复习课（第5课时）【导学】在本章中，我们探索了直角三角形的三边关系，并在此基础上得到了勾股定理，并学习了如何利用拼图验证勾股定理，介绍了勾股定理的用途；本章后半部分学习了勾股定理的逆定理以及它的应用．其知识结构如下：1.勾股定理：(1)直角三角形两直角边的______和等于_______的平方．就是说，对于任意的直角三角形，如果它的两条直角边分别为a 、b ，斜边为c ，那么一定有：————————————.这就是勾股定理．(2)勾股定理揭示了直角三角形__ _之间的数量关系，是解决有关线段计算问题的重要依据． 勾股定理的探索与验证，一般采用“构造法”．通过构造几何图形，并计算图形面积得出一个等式，从而得出或验证勾股定理．2.勾股定理逆定理“若三角形的两条边的平方和等于第三边的平方，则这个三角形为________.”3.勾股定理的应用：（1）已知直角三角形的两边，求 ；（2）勾股定理的逆定理是用来判定一个三角形是否是直角三角形的.勾股定理的逆定理也可用来证明两直线是否垂直,勾股定理是直角三角形的性质定理，而勾股定理的逆定理是直角三角形的判定定理，它不仅可以判定三角形是否为直角三角形，还可以判定哪一个角是 ，从而产生了证明两直线互相垂直的新方法：利用勾股定理的逆定理，通过计算来证明，体现了 的思想．4.三角形的三边分别为a 、b 、c ，其中c 为最大边，若222c b a =+，则三角形是直角三角形；若222c b a >+，则三角形是 ；若2<+c b a 22，则三角形是 ．所以使用勾股定理的逆定理时首先要确定三角形的最大边．【典型例题】例1.如果ΔABC 的三边分别为a 、b 、c ，且满足a 2+b 2+c 2+50=6a+8b+10c ，判断ΔABC 的形状。

思路点拨：要判断ΔABC 的形状，需要找到a 、b 、c 的关系，而题目中只有条件a 2+b 2+c 2+50=6a+8b+10c ，故只有从该条件入手，解决问题总结升华：勾股定理的逆定理是通过数量关系来研究图形的位置关系的,在证明中也常要用到。

成都市东湖中学八上数学《一次函数动点》导学案1、已知如图，直线与x轴相交于点A，与直线相交于点P。

（1）求点P的坐标；（2）求的值；（3）动点E从原点O出发，沿着O-P-A的路线向点A匀速运动（E不与点O、A 重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B。

设运动t秒时，F的坐标为（a，0），矩形EBOF与重叠部分的面积为S。

求S与a之间的函数关系式。

2、如图，在平面直角坐标系内，直线1+=x y 与343+-=x y 交于点A ，分别交x 轴于点B 和点C ，点D 是直线AC 上的一个动点。

（1）求点A 、B 、C 的坐标；（2）当△CBD 为等腰三角形时，求点D 的坐标。

３、如图，矩形ABCD 的两条边在坐标轴上，点D 与原点重合，对角线BD 所在直线的函数关系式为x y 43=，AD=8，矩形ABCD 沿DB 方向以每秒1个单位长度运动，同时点P 从点A 出发做匀速运动，沿矩形ABCD 的边经过点B 到达点C ，用了14秒。

（1）求矩形ABCD 的周长；（2）如图所示，图形运动到第5秒时，求点D 的坐标；（3）设矩形运动的时间为t ，当60≤≤t 时，点P 所经过的路线是一条线段，请求出线段所在直线的函数关系式。

４、如图1，在矩形ABCD 中，AB=12cm ，BC=6cm ，点P 从A 点出发，沿A —B —C —D 的路线运动，到D 点停止；点Q 从D 点出发，沿D —C —B —A 运动，到A 点停止。

若点P 、点Q 同时出发，点P 的速度为每秒1厘米，点Q 的速度为每秒2厘米，a 秒时点P 、点Q 同时改变速度。

如图2是描述点P 出发x 秒后△APD 的面积1S （平方厘米）与x 秒的函数关系的图像。

图3描述的是点Q 出发x 秒后△AQD 的面积2S （平方厘米）与x 秒的函数关系的图像。

根据图像：（1）求a 的值和点P 改变后的速度；（2）设点P 离开点A 的路程为1y （厘米），点Q 到点A 还需要走的路程为2y （厘米），请分别写出改变速度后1y 、2y 与出发后的运动时间x （秒）的函数关系式，并求出P 与Q 相遇时x 的值。

成都市东湖中学八上数学《平面直角坐标系》导学【学习目标】1、理解平面直角坐标系的有关概念，能正确画出直角坐标系。

2、能在平面直角坐标系中，根据坐标找出点，由点求出坐标。

3、解平面内的点与有序实数对之间的一一对应关系。

【学习重难点】重点：面直角坐标系及其有关概念，根据坐标找点，由点求坐标。

难点：点的坐标的表示。

【学习方法】自主探究与小组合作【学习过程】一、学习准备1、在生活中，确定点的位置最少需要个独立的数据。

2、确定点的位置的方法主要有、、、、等。

3、规定了、、的直线叫数轴。

数轴和实数是关系。

二、教材精析活动1：探究坐标系1（1）如图1是某市的旅游示意图，在科技大学处的你如何向来访的朋友介绍该市几个风景点的位置呢?尽可能给出简洁的表示方法，并与同伴交流。

大成殿：，中心广场：，碑林：。

(排版说明:加上比例尺，一格表示100m)（2）小明用（0,0）表示科技大学的位置，用（2，5）表示大成殿，你理解他的意思吗？试表示出图中其他点的位置。

（3）按照小明的方法，（5,2）表示，（5,2）中的2表示，（2,5）中的2表示。

2（1）站在中心广场的小亮，以中心广场为“原点”，怎样用数对表示各景点的位置呢？归纳：1.平面直角坐标系的概念在平面内，两条互相垂直且有公共原点的数轴组成。

通常，两条数轴分别置于水平位置和铅直位置，取向和向为正方向。

其中水平的数轴称为轴或轴，铅直的数轴称为轴或轴。

横轴和纵轴统称 .公共的原点O称为直角坐标系的原点。

两条数轴把平面分为四部分，右上部分为第象限，其余按逆时针分别为第二、三、四象限。

特别的坐标轴上的点任何象限。

2、点的坐标的表示在平面直角坐标系中，要想表示一个点的位置，就要用它的“坐标”来表示。

如图，对于平面内任意一点P，过点P分别向x轴、y轴作，垂足在x轴、y轴上对应的数a、b分别叫做点P的、；有序数图1 图2 图3（2）如图2，小明用（0,0）表示科技大学的位置，用（2，5）表示大成殿，你理解他的意思吗？按照小明的方法，（5,2）表示，（5,2）中的2表示，（2,5）中的2表示。