下载文档原格式
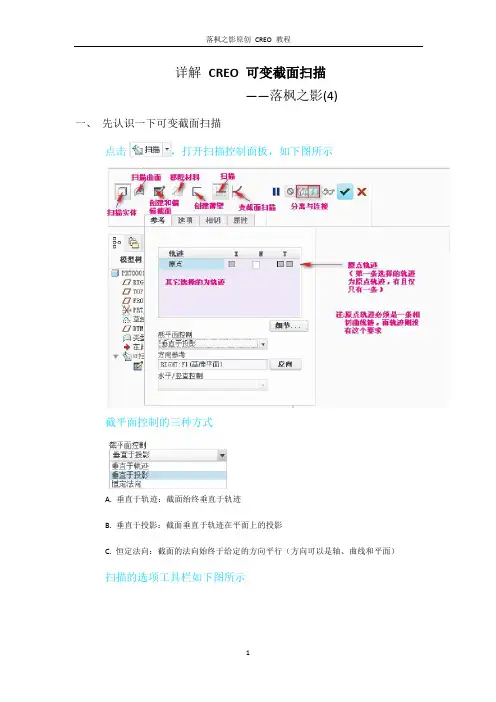
落枫之影原创 CREO 教程详解 CREO 可变截面扫描——落枫之影(4)一、先认识一下可变截面扫描点击，打开扫描控制面板，如下图所示截平面控制的三种方式A. 垂直于轨迹：截面绐终垂直于轨迹B. 垂直于投影：截面垂直于轨迹在平面上的投影C. 恒定法向：截面的法向始终于给定的方向平行（方向可以是轴、曲线和平面）扫描的选项工具栏如下图所示1落枫之影原创 CREO 教程封闭端点：扫描曲面时是否封闭端点扫描的相切工具栏如下图所示可选取其他参考的轨迹曲线进行特征扫描二、变截面扫描一般应用1.绘制如下图所示模型2绘制此图的方法有很多，我想使用变截面扫描后会节省很多麻烦前几步我就不说了，重点讲解变截面扫描：退出草绘，打开扫描工具，依次选择这三条草绘曲线点击创建截面，绘制如下图所示图形退出草绘，预览特征，如下图所示确定，完成绘制到这里我们已经画好了一个，大家可能发现变截面扫描出来的实体好像与原来的实体中间有裂缝，怎么会这样呢其实问题很好解决，那还得从草绘轨迹说起啦修改草绘，更改如下图所示5退出草绘，重新生成，然后再环形阵列一下，如下图所示通过上面那个例子，我们初步认识了可变截面扫描2.可变截面扫描的辅助轨迹可以有很多条。
但原点轨迹必须只有一条。
下面再通过另外一个例子来向大家阐述可变截面扫描的强大之处仅用一个变截面扫描特征就可以绘制一把十字螺丝刀a.在使用可变截面扫描前，必须先绘制好轨迹曲线注意：这条线仅用来确定剖面曲线所在平面位置，并非轨迹曲线b.创建基准平面（选择直线上打断的点和 TOP 平面）7c.创建完平自面，下面就要画剖面曲线啦8d.打开变截面扫描的控制面板，按 ctrl 键依次选择轨迹e.点击，进入草绘截面，绘制如图所示的截面退出草绘f.完成绘制，至如螺丝刀的十字，我单独做一个特征来讲解还是变截面扫描,这次要用到关系函数使用函数退出变截面扫描完成十字螺丝刀的绘制三、变截面扫描高级应用注意：此部分内容，只写关键步骤，不懂的请自行摸索1. 使用关系函数来控制截面（方向盘）扫描的截面如下图示完成后效果2. 使用关系函数来控制截面（齿形离合器）12a,草绘两条轨迹线b.新建基准点,,c.草绘截面，标注尺寸时请以经过基准点的轴线为参考d.退出变截面扫描3. 使用 trajpar 函数来控制截面（双绞线、四绞线、凸轮等）先来看一下四绞线14草绘一条扫描轨迹进入变截面扫描，选取上面的轨迹，然后草绘如下图所的截面使用关系驱动尺寸15退出草绘，完成绘制同理双绞线的画法也是如此，请自行绘制4. 使用图形来控制变截面这道题目很简单，主要用来练习一下图形的使用16使用图形基准新建一个名为“tu”的图形，绘制如图所示曲线17再新建一个名为”tu2”的图形，绘制如下图所示曲线草绘一条轨迹曲线，作为原始轨迹进入变截面扫描，选取轨迹，草绘截面18退出草绘后面的工作就麻烦你们自行完成讲到图形，大家很快就会想到凸轮，没错，用图形控制凸轮轨迹比使用二次投影曲线是要精准很多，也容易修改。
VSS扫描详解BY:王庆丰VSS也叫可变截面扫描一、首先，我们来理解一下扫描。
如下图：1.用一个不变的截面（位置和大小都不变）沿着一条轨迹线扫描过去。
此轨迹线就是原点轨迹线，其含义就是扫描过种中不管是哪个截面，他的原点始终是在这条线上。
有且只有一条，且必须第一个选。
2.如果只是确定好截面的原点，截面的位置还没有完全确定下来。
扫描过程默认截面垂直于原点轨迹。
所以截面在空间的位置就完全确定了。
3.起点和终点位置可以改，不一定要是草绘线的起点和终点。
只要改图中数字（0.000）即可。
如果是正数，即扫描长度大于轨迹线长度时，加长部份的轨迹线是什么样呢？加长部份是直线且长度等你改的数值，且与草绘线的起点或终点相切终点起点二、可变截面扫描其特点是：截面是可以变化的扫描。
截面的变化有两种1.截面大小变了，如下图：Sd3=40+trajpar*100≤Trajpar≤1扫描过程中截面中的一条边从40变到50，起始点的时候是40，终点的时候是50也就是说在起始点时截面是一个40*sd4的矩形。
终点时截面是一个50*sd4的矩形。
（上图中sd4是固定值，当然也可以变化）截平面默认为垂直于轨迹。
(方向控制下面讲，暂时用垂直于轨迹)2.截面的位置变了。
如上图，截面大小没变，只是矩形的下面一条边相对原点轨迹线的位置变了。
位置由起始点的10变到终点的50。
（截平面默认为垂直于轨迹）说明：Trajpar与原点轨迹线对应。
Trajpar=0。
说明截面处在原点轨迹线的起点Trajpar=1。
说明截面处在原点轨迹线的终点特别的当Trajpar=0.5时。
说明截面处在原点轨迹线的中点。
我们来验证一下一般情况。
当Trajpar=0.3时sd5=10+trajpar*50=10+0.3+50=25。
新建一个点。
选原点轨迹线。
比率0.3过该点作一个平面，与轨迹线垂直。
建一个截面，新建工程图与计算结果一致。
总结：截面的变化可以是大小或位置。
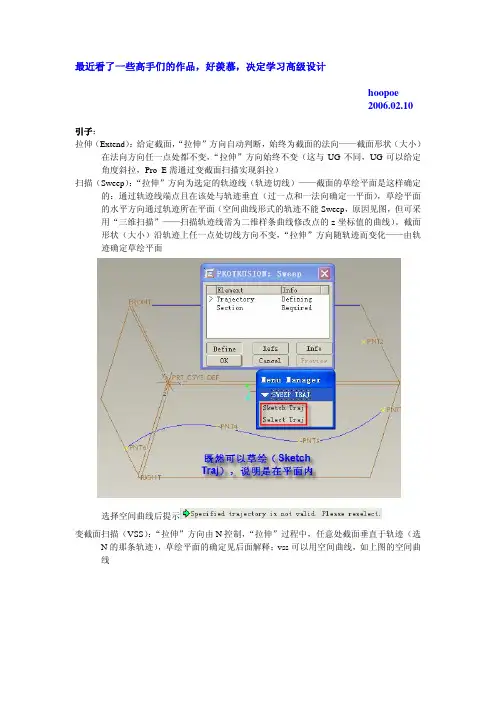
最近看了一些高手们的作品，好羡慕，决定学习高级设计hoopoe2006.02.10引子：拉伸（Extend）：给定截面，“拉伸”方向自动判断，始终为截面的法向——截面形状（大小）在法向方向任一点处都不变，“拉伸”方向始终不变（这与UG不同，UG可以给定角度斜拉，Pro_E需通过变截面扫描实现斜拉）扫描（Sweep）：“拉伸”方向为选定的轨迹线（轨迹切线）——截面的草绘平面是这样确定的：通过轨迹线端点且在该处与轨迹垂直（过一点和一法向确定一平面），草绘平面的水平方向通过轨迹所在平面（空间曲线形式的轨迹不能Sweep，原因见图，但可采用“三维扫描”——扫描轨迹线需为二维样条曲线修改点的z坐标值的曲线）。
截面形状（大小）沿轨迹上任一点处切线方向不变，“拉伸”方向随轨迹而变化——由轨迹确定草绘平面选择空间曲线后提示变截面扫描（VSS）：“拉伸”方向由N控制，“拉伸”过程中，任意处截面垂直于轨迹（选N的那条轨迹），草绘平面的确定见后面解释；vss可以用空间曲线，如上图的空间曲线Trajectories不同情况下vss效果1扫描过程中截面定向的控制为垂直轨迹（Normal To Trajectory）atop与front如下截面在扫描过程中截面始终垂直原始轨迹（Origin）——Origin栏中N选中——N代表截面的法向，即截面的Z方向，扫描过程中截面的X方向自动判断。
且截面经过所有轨迹bcd vss不成功e 与a一样fg 与b一样当Chain1和Chain3是直线时，结果如下hi与c一样截面在扫描过程中，截面的X向量和法向量始终是垂直的（即X和N），所以，X向量只有在垂直原始轨迹（Origin）时才有意义，所以Chain选中（i的情况）与未选中（c的情况）一样，因为Chain2与Origin自始至终没有垂直的情况发生看看N控制什么？看vss2.prt可以看出，N控制截面的法向，X控制截面的X方向，若X为某直线，则截面在vss中不发生扭曲（旋转），所以，X控制截面在vss过程中截面绕Z 方向（即N）的旋转趋势学习手记：1 Origin Trajectory (原点轨迹线)：在扫描过程中，二维截面的原点(Origin)永远落在此轨迹线(注意：绘制二维截面时，系统会自动在画面上呈现x轴和y轴，其交点即为原点)。
可变截面扫描－指令详细解说不管版本如何变更，可变扫出始终是我比较偏爱的造型指令。
这是因为可变扫出除了可以得到相对规则的曲面外，它丰富的控制属性和可以预见的结果形状让它更能在适当的场合发挥作用。
可变扫出的控制主要有下面的几项：轨迹，截面的定向和截面的形状1．轨迹在可变扫出中有两类轨迹，有且只有一条称之为原始轨迹（Origin）也就是你第一条选择的轨迹。
原始轨迹必须是一条相切的曲线链（对于轨迹则没有这个要求）。
除了原始轨迹外，其它的都是轨迹，一个可变扫出指令可以有多条轨迹。
在wildfire以后的版本中，原始轨迹和轨迹的功能性差异除了这点外可以说没有任何差异了；截面的定向依赖于两个方向的确定：Z方向和X方向。
注意看上面的图片你会发现在每条轨迹后面都有三个可选项分别用X，N和T作标题，它们分别代表的是X向量，Normal（垂直方向也就是Z方向）以及T angency切向参考，在对应的方框内打勾就表明采用该选项；显然对于可变扫出只能有一个X向量和一个Z方向，所以你选择了某个轨迹后会自动曲线其它轨迹中对应的选择；对于切向参考，因为一条轨迹很可能是两面链的交线，所以有两个框来供你选择不同的面链。
当然你也可以手工选择作为切向参考的面链。
在下面的Section Plane Control下拉框中，你可以选择你的截面的定向方法，缺省是Norma To Trajectory是由轨迹来确定截面的定向，但是你也可以用其它两个选项来确定：最下面就是水平竖直方向的确定，这可以在Horzontal/Vertical Control下拉框中进行选择。
下面就来具体看一下各种组合的截面定向方法的表现形式：2．切向参考（Tangency）很多人都知道用切向参考可以实现扫出面和已有的面实现相切连接，但如果仅是局限于定义面相切的话那就是人为的把这个选项的作用局限在一个点上了，事实上利用这个选项你可以把你的扫出面定以成和参考面成任何角度关系（当然也包括相切的0度关系）。
详解CREO 可变截面扫描——落枫之影(4)一、先认识一下可变截面扫描点击，打开扫描控制面板，如下图所示截平面控制的三种方式A. 垂直于轨迹：截面绐终垂直于轨迹B. 垂直于投影：截面垂直于轨迹在平面上的投影C. 恒定法向：截面的法向始终于给定的方向平行（方向可以是轴、曲线和平面）扫描的选项工具栏如下图所示封闭端点：扫描曲面时是否封闭端点扫描的相切工具栏如下图所示可选取其他参考的轨迹曲线进行特征扫描二、变截面扫描一般应用1.绘制如下图所示模型绘制此图的方法有很多，我想使用变截面扫描后会节省很多麻烦前几步我就不说了，重点讲解变截面扫描：退出草绘，打开扫描工具，依次选择这三条草绘曲线点击创建截面，绘制如下图所示图形退出草绘，预览特征，如下图所示确定，完成绘制到这里我们已经画好了一个，大家可能发现变截面扫描出来的实体好像与原来的实体中间有裂缝，怎么会这样呢其实问题很好解决，那还得从草绘轨迹说起啦修改草绘，更改如下图所示退出草绘，重新生成，然后再环形阵列一下，如下图所示通过上面那个例子，我们初步认识了可变截面扫描2.可变截面扫描的辅助轨迹可以有很多条。
但原点轨迹必须只有一条。
下面再通过另外一个例子来向大家阐述可变截面扫描的强大之处仅用一个变截面扫描特征就可以绘制一把十字螺丝刀a.在使用可变截面扫描前，必须先绘制好轨迹曲线注意：这条线仅用来确定剖面曲线所在平面位置，并非轨迹曲线b.创建基准平面（选择直线上打断的点和TOP 平面）c.创建完平自面，下面就要画剖面曲线啦d.打开变截面扫描的控制面板，按ctrl 键依次选择轨迹e.点击，进入草绘截面，绘制如图所示的截面退出草绘f.完成绘制，至如螺丝刀的十字，我单独做一个特征来讲解还是变截面扫描,这次要用到关系函数使用函数退出变截面扫描完成十字螺丝刀的绘制三、变截面扫描高级应用注意：此部分内容，只写关键步骤，不懂的请自行摸索1. 使用关系函数来控制截面（方向盘）扫描的截面如下图示完成后效果2. 使用关系函数来控制截面（齿形离合器）a,草绘两条轨迹线b.新建基准点,,c.草绘截面，标注尺寸时请以经过基准点的轴线为参考d.退出变截面扫描3. 使用trajpar 函数来控制截面（双绞线、四绞线、凸轮等）先来看一下四绞线草绘一条扫描轨迹进入变截面扫描，选取上面的轨迹，然后草绘如下图所的截面使用关系驱动尺寸退出草绘，完成绘制同理双绞线的画法也是如此，请自行绘制4. 使用图形来控制变截面这道题目很简单，主要用来练习一下图形的使用使用图形基准新建一个名为“tu”的图形，绘制如图所示曲线再新建一个名为”tu2”的图形，绘制如下图所示曲线草绘一条轨迹曲线，作为原始轨迹进入变截面扫描，选取轨迹，草绘截面退出草绘后面的工作就麻烦你们自行完成讲到图形，大家很快就会想到凸轮，没错，用图形控制凸轮轨迹比使用二次投影曲线是要精准很多，也容易修改。
详 扫——落枫之影(413624704) 一、先认识一下可变截面扫描点击，打开扫描控制面板，如下图所示截平面控制的三种方式A.垂直于轨迹：截面绐终垂直于轨迹B.垂直于投影：截面垂直于轨迹在平面上的投影C.恒定法向：截面的法向始终于给定的方向平行（方向可以是轴、曲线和平面）扫描的选项工具栏如下图所示封闭端点：扫描曲面时是否封闭端点扫描的相切工具栏如下图所示可选取其他参考的轨迹曲线进行特征扫描二、变截面扫描一般应用1.绘制如下图所示模型绘制此图的方法有很多，我想使用变截面扫描后会节省很多麻烦 前几步我就不说了，重点讲解变截面扫描：退出草绘，打开扫描工具，依次选择这三条草绘曲线点击创建截面，绘制如下图所示图形退出草绘，预览特征，如下图所示确定，完成绘制到这里我们已经画好了一个，大家可能发现变截面扫描出来的实体好像与原来的实体中间有裂缝，怎么会这样呢？其实问题很好解决，那还得从草绘轨迹说起啦修改草绘，更改如下图所示退出草绘，重新生成，然后再环形阵列一下，如下图所示通过上面那个例子，我们初步认识了可变截面扫描2.可变截面扫描的辅助轨迹可以有很多条。
但原点轨迹必须只有一条。
下面再通过另外一个例子来向大家阐述可变截面扫描的强大之处仅用一个变截面扫描特征就可以绘制一把十字螺丝刀a.在使用可变截面扫描前，必须先绘制好轨迹曲线注意：这条线仅用来确定剖面曲线所在平面位置，并非轨迹曲线b.创建基准平面（选择直线上打断的点和TOP平面）c.创建完平自面，下面就要画剖面曲线啦d.打开变截面扫描的控制面板，按ctrl键依次选择轨迹e.点击，进入草绘截面，绘制如图所示的截面退出草绘f.完成绘制，至如螺丝刀的十字，我单独做一个特征来讲解 还是变截面扫描,这次要用到关系函数使用函数退出变截面扫描完成十字螺丝刀的绘制三、变截面扫描高级应用注意：此部分内容，只写关键步骤，不懂的请自行摸索 1.使用关系函数来控制截面（方向盘）扫描的截面如下图示完成后效果2.使用关系函数来控制截面（齿形离合器）a,草绘两条轨迹线b.新建基准点,,c.草绘截面，标注尺寸时请以经过基准点的轴线为参考d.退出变截面扫描3.使用trajpar函数来控制截面（双绞线、四绞线、凸轮等）先来看一下四绞线草绘一条扫描轨迹进入变截面扫描，选取上面的轨迹，然后草绘如下图所的截面使用关系驱动尺寸退出草绘，完成绘制同理双绞线的画法也是如此，请自行绘制4.使用图形来控制变截面这道题目很简单，主要用来练习一下图形的使用使用图形基准新建一个名为“tu”的图形，绘制如图所示曲线再新建一个名为”tu2”的图形，绘制如下图所示曲线草绘一条轨迹曲线，作为原始轨迹进入变截面扫描，选取轨迹，草绘截面退出草绘后面的工作就麻烦你们自行完成讲到图形，大家很快就会想到凸轮，没错，用图形控制凸轮轨迹比使用二次投影曲线是要精准很多，也容易修改。
Proe圆轨迹可变扫描是无维网站长IceFai在2004年所创造的在Pro/Engineerr软件上进行曲面造型的一种方法，方法主要针对一些不规则轮廓隆起的曲面。
这个方法因为操作简单、适用性广并且得到的曲面质量高而为广大Proe用户所采用。
到现在在Proe 用户应用非常广泛，本教程详细讲解了圆轨迹可变扫描的基本扫描的基本实现方法，同时也对这些年来不同的用户反馈回来的使用上遇到的各种问题做了一次性的全面解答。
圆轨迹可变扫描通过增加一个圆作为原始轨迹结合产品的外观轮廓曲线进行可变扫描方法来创建曲面，使用这个方法所创建的曲面就类似于使用旋转特征所创建的旋转曲面，不同的是普通的旋转得到的轮廓是圆，而这个方法的轮廓则可以是自由形状。
典型的通过圆轨迹可变扫描所创建的曲面如图1和图2所示：对下面的案例，要使用如图3所示的平面不规则轮廓曲线，创建一个高度为20的弧形曲面。
对于这样的曲面看起来比较简单，但如果采用传统的够线加截面进行边界混成的方法，得到的曲面质量不高，并且操作起来也相当繁锁。
下面就来看看如何运用圆轨迹可变扫描进行这样的曲面的创建。
第一步，首先确定弧形曲面的最高点，然后在轮廓曲线所在的平面上对应这个最高点的投影位置下草绘一个基准点PNTO。
第二步，在轮廓曲线所在的平面上，以前面所创建的基准点PNTO为圆心，草绘一个一定大小的圆（图5），这个圆的直径可以随意但不能太小，否则会可能导致失败，其中的原因后面将会有讲解。
第三步，采用上一步所创建的圆作为原始轨迹，轮廓曲线作为轨迹进行可变扫描（图6）。
第四步，进入可变扫描的草绘截面环境，这一步是整个方法成功与否的关键地，很多用户就是因为草绘中所选的参考和约束方法不当导致可变扫描的失败，所以务必看清楚下面的步骤并且能够仔细思考理清楚其中的原理。
选择第一步所确定的中心基准点PNTO作为草绘参考（图7），在这一步中，很多用候，不少用户就直接选择了其中一个基准曲面做为参考，从而导致最终的失败，其实只需要仔细考虑一下在整个可变扫描过程中，所选择的参考是否还能够一样的存在就可以了，显然选择基准平面的话，当轨迹转一个方向后这个基准平面不再和草绘截面法向，自然也不会再有这个参考存在了。
ProE可变截面扫描关系式1. 任务概述本文将介绍ProE软件中的可变截面扫描关系式，包括其定义、用途、使用方法和注意事项等内容。
通过阅读本文，读者将了解到如何利用ProE软件中的可变截面扫描关系式来实现复杂形状的设计和建模。
2. 可变截面扫描关系式的定义可变截面扫描关系式是ProE软件中的一种功能，它允许用户通过定义一个或多个曲线来创建一个二维或三维的几何形状。
这些曲线可以是直线、圆弧、椭圆等，用户可以根据需要自由选择。
通过调整曲线参数，用户可以实现对几何形状的灵活控制。
3. 可变截面扫描关系式的用途可变截面扫描关系式在工程设计和建模中有着广泛的应用。
它可以用于创建复杂的曲线、表面和体积模型，以满足不同产品设计和制造过程中的要求。
例如，在航空航天领域中，可变截面扫描关系式常被用来设计飞机机翼的气动外形，以提高飞行性能和燃油效率。
4. 可变截面扫描关系式的使用方法在ProE软件中，使用可变截面扫描关系式可以按照以下步骤进行：步骤1：选择绘制曲线的工具打开ProE软件后，在绘图工具栏中选择适合的曲线绘制工具，如直线、圆弧或椭圆等。
步骤2：绘制曲线使用所选工具在绘图区域中绘制曲线。
可以根据需要设置起点、终点和其他必要的参数。
可以通过调整控制点来改变曲线的形状。
步骤3：定义扫描路径在完成曲线绘制后，选择“可变截面扫描”功能，并定义一个或多个扫描路径。
扫描路径是指沿着哪些方向对曲线进行扫描，以创建几何形状。
步骤4：调整参数根据需要，可以调整各种参数来控制几何形状的外观和尺寸。
这些参数包括曲线长度、角度、半径等。
通过不断调整参数，可以实现对几何形状的精确控制。
步骤5：生成模型完成参数调整后，可以点击“生成模型”按钮来生成几何模型。
ProE软件会根据所定义的曲线和扫描路径自动生成相应的几何形状。
5. 注意事项在使用可变截面扫描关系式时，需要注意以下事项：•确保所绘制的曲线和定义的扫描路径符合设计要求，避免出现错误或失真。
VSS扫描详解BY:王庆丰VSS也叫可变截面扫描一、首先，我们来理解一下扫描。
如下图：1.用一个不变的截面（位置和大小都不变）沿着一条轨迹线扫描过去。
此轨迹线就是原点轨迹线，其含义就是扫描过种中不管是哪个截面，他的原点始终是在这条线上。
有且只有一条，且必须第一个选。
2.如果只是确定好截面的原点，截面的位置还没有完全确定下来。
扫描过程默认截面垂直于原点轨迹。
所以截面在空间的位置就完全确定了。
3.起点和终点位置可以改，不一定要是草绘线的起点和终点。
只要改图中数字（0.000）即可。
如果是正数，即扫描长度大于轨迹线长度时，加长部份的轨迹线是什么样呢？加长部份是直线且长度等你改的数值，且与草绘线的起点或终点相切终点起点二、可变截面扫描其特点是：截面是可以变化的扫描。
截面的变化有两种1.截面大小变了，如下图：Sd3=40+trajpar*100≤Trajpar≤1扫描过程中截面中的一条边从40变到50，起始点的时候是40，终点的时候是50也就是说在起始点时截面是一个40*sd4的矩形。
终点时截面是一个50*sd4的矩形。
（上图中sd4是固定值，当然也可以变化）截平面默认为垂直于轨迹。
(方向控制下面讲，暂时用垂直于轨迹)2.截面的位置变了。
如上图，截面大小没变，只是矩形的下面一条边相对原点轨迹线的位置变了。
位置由起始点的10变到终点的50。
（截平面默认为垂直于轨迹）说明：Trajpar与原点轨迹线对应。
Trajpar=0。
说明截面处在原点轨迹线的起点Trajpar=1。
说明截面处在原点轨迹线的终点特别的当Trajpar=0.5时。
说明截面处在原点轨迹线的中点。
我们来验证一下一般情况。
当Trajpar=0.3时sd5=10+trajpar*50=10+0.3+50=25。
新建一个点。
选原点轨迹线。
比率0.3过该点作一个平面，与轨迹线垂直。
建一个截面，新建工程图与计算结果一致。
总结：截面的变化可以是大小或位置。
可以是单个的尺寸也可是多个尺寸同时变化，可以是线性尺寸，也可以是角度尺寸。
当然截面大小或位置的控制不一定只能用关系式。
可以用别的轨迹线或图形函数。
后面再讲以上几个例子只讲了截面，对于截面的方向都是用Creo默认的“垂直于轨迹”对于空间的任意一个截面，如果只知道一个原点是不能完全确定这个截面的。
所以接下来我们进一步来确定截面。
那么下一步就是确定Z方向了。
Z方向原点确认好了后，我们接下来确定Z方向，之所以称为Z方向而不称Z 轴，是因为截面坐标系是一个二维的X-Y坐标系，但截面要做移动扫描，将其移动方向称为Z方向。
确定Z方向时，CREO给出了三种方法：1.垂直于轨迹你可以在面板的“N”项中任选一条轨迹让扫描截面垂直于该轨迹，称为N轨迹。
N轨迹可以是原点轨迹，也可以是一般轨迹。
扫描截面在扫描移动过程中始终垂直于N轨迹，即N轨迹切向即是Z方向。
2.垂直于投影截面垂直于轨迹在平面上的投影。
即我们可以选一条轨迹线在平面上投影的切向作为Z方向。
3.恒定法向截面的法向（Z方向）始终与给定的方向平行。
方向可以是轴，曲线，平面。
X轴到现在为止我们已经确认了坐标系原点和Z方向。
下面我们确定二维截面的X方向。
即参考选项里的“水平/垂直控制”。
CREO缺省状态下会自动根据原点轨迹的法向确定X轴。
你也可以在“X”项中任选一条轨迹线。
该轨迹线与扫描截面有一点交点，该交点与坐标系原点的连线即为X轴。
注意：X轨迹不能与原点轨迹相交，因为两点才能确定一条直线，一相交就表明坐标原点和交点重合了，X轴给不出来。
过一点有无数条直线。
原点轨迹与N轨迹原点轨迹有且只有一条。
而且必须先选。
原点轨迹必须光滑。
不能有尖点。
（高等数学知识好的能理解，不能理解的就记住算了）当我们Z方向用“垂直于轨迹控制”时，可以选另外一条链作为Z方向轨迹。
也可以用原点轨迹是原点轨迹亦是N轨迹垂直于投影与恒定法向非常简单。
不作介绍。
X轨迹当Z确定好后，最后我们确定X就可以把截面完全确定了。
（Y轴根据右手螺旋法则确定）我们可以指其他任意一条轨迹为X轨迹。
是原点轨迹亦是N轨迹如上图：原点轨迹和N轨迹是一条。
链1为X轨迹。
我们还是以一般情况来举例说明。
设trajpar=0.3在“链1”上建一个点。
比率=0.3。
建一个平面，经过上面所建的点且垂直于N轨迹。
再建一个点。
N轨迹与上面所建平面的交点。
建一条直线，连接PNT0和PNT1点。
从PNT1到PNT0的方向就是X方向。
很显然，如果原点轨迹和X相交。
则PNT1和PNT0在扫描过程中就会重合。
此时X则不能确定，扫描失败。
至此，截面完全确定了。
如下图：上图实际上说明：当trajpar=0.3时。
可变截面的位置情况。
截面的控制方法1.函数关系实际上前面讲的例子就是用函数关系来控制截面的。
当然例子非常的简单，主要用到的数学函数有sin()及cos()。
a.草绘轨迹b.进入VSS选择上面的草绘为原点轨迹Z方向垂直于轨迹（上面草绘的线即是原点轨迹与是N轨迹）。
X轴自动c.草绘一个圆，标注圆的直径。
d.写关系式：sd3=100+sin(trajpar*360*15)*10其意义是： Trajpar对应整个草绘线Trajpar=0时，截面在起始点Trajpar=1时，截面在终点。
由于函数sin()是周期函数，sin(trajpar*360*15) 其最小正周期T=1/15，说明在整个扫描过程中sd3这个尺寸走了15个周期。
特别的当：Trajpar=1/15时。
Sd3=100读者可按上面的方法自行验证。
完成如果如下图关系式函数a.草绘轨迹b.进入VSS，选上一步建产的草绘为原点轨迹，Z方向垂直于轨迹，X轴自动c.草绘一个圆，加上关系式if trajpar>0.25&trajpar<0.75sd3=50+sin(trajpar*360*50)*5elsesd3=50endif此关系式相当一个分段函数Y=50+5*sin(x*360*5) x∈(0.25,0.75)Y=50 X∈[0,0.25]或者[0.75,1]2.轨迹有时候并不知道函数关系，可以通过附加轨迹线来控制截面中间的链是原点轨迹也是N轨迹。
链1和链2分别用来控制截面。
扫描过程中，截面上有一个点始终链1上，另外一个点在链2上。
一步VSS下图：分析：用一个与Front平面平行的平面去截此零件，其截面都是矩形，矩形高度都是一样。
只是宽度在中间有一段是变化的。
那我们把宽度用辅助轨迹去控制。
具体步奏：a.草绘轨迹b.进入VSS，先选直线为原点轨迹。
再按Ctrl选上右边的草绘线。
c.进入草绘，草绘一矩形。
两端点分别与原点轨迹和辅助轨迹重合。
点确定，完成。
3.图形3.1.图形特征从图标就可以很形象的看出来。
图形特征就是指函数的图形或者说曲线。
有些函数写关系式太麻烦，有些甚至写不出来。
这时候用图形特征来表达更合适。
下面看一个简单的例子。
点基准下的国“图形”系统提示为特征输入一个名字可以输入中文，确定。
既然是函数的图形，首先建一个坐标系按右图草绘。
很显然，此图形是一个分段函数。
当0≤x≤10 y=x当10＜x≤20 y=103.2.Creo曲线表计算函数利用曲线表计算函数，可使用曲线表特征通过关系驱动尺寸。
这些尺寸可为截面、零件或装配尺寸。
格式如下：evalgraph("graph_name", x)其中：•graph_name- 曲线表的名称。
x- 是沿曲线表 x 轴的值，为其返回 y 值。
我们先来一个非常简单的例子帮助大家理解a.建一个图形特征。
b.草绘一条直线。
长度16c.进入VSS。
截面画一个圆。
标注圆的直径d.写上关系式：sd3=evalgraph("图形_1",trajpar*16)完成如图：这时候有人可能会说：搞那么麻烦，直接旋转不就得了。
我只是通过简单的例子来说明曲线表函数。
前面多次说过，Trajpar=0及Trajpar=1 时,是代表扫描的起点和终点。
当Trajpar=0时，Trajpar*16=0，evalgraph("图形_1",trajpar*16)=？看下图，很显然：evalgraph("图形_1",trajpar*16)=5 即x=0时，Y的值所以Trajpar=0时，sd3=5上图还标出了。
Trajpar=1时，sd3=10.815再例如：Trajpar=0.75时，Trajpar*16=0.75*16=12sd3取图形上X=12时的Y值。
Y=11.223.即sd3=11.223 注意：写关系式时，trajpar后的系数最好要与图形上的X 对应。
因为trajpar的范围是【0，1】如上面的例子，图形没变。
在写关系的时候把“trajpar*16”写成了“trajpar*12”了。
当trajpar=1，时，指的是扫描的终点。
这时候sd3=11.223。
而不是10.815读者可以自己验证trajpar等于其他值的情况。
另外一种情况。
如果把“trajpar*16”写成了“trajpar*20”了。
当trajpar=1时。
X=20，图形上没有Y的值。
这时系统会把16＜X≤20的值找出来的。
见下图中红色线段虽然Creo不会把这条直线段画出来。
但Y的取值按这条直线段取。
这条直线段与图形在X=16处相切。
终点坐标为x=20凸轮a.建图形特征b.草绘一个直径200的圆。
并建轴线c.进入VSS。
选草绘圆为原点轨迹，Z方向垂直于轨迹。
d.选取轴线为草绘截面参考。
草绘一个矩形。
右边与轴重合。
e.输入关系sd4=evalgraph("1",trajpar*360)f.确定，完成。
通常，我们做凸轮时，图形中的X指的是角度。
扫描时指是曲线长度。
但是，曲线长度和角度正好是成正比关系。
弧长=圆心角*半径。
正好可以对应。
也就是说：Trajpar*360这个角度，正好在这个圆心角的弧长上。
常用函数前面已经介绍过几个，如：sin(),cos(),evalgraph() 下面详细介绍几个。
并通过实例讲解其中一些函数的用法1.abs()abs() 为绝对值函数2.sqrt()sqrt()开平方函数。
也可以实现绝对函数一样的功能。
如sqrt(t^2)等价于abs(t)3.ceil()与floor()ceil() 为不小于其值的最小整数floor()不大于其值的最大整数如:ceil(2.56)=3，ceil(-2.5)=-2floor(2.56)=2 floor(-2.5)=-3括号内可以是实数类型参数可以给函数ceil和floor加一个可选的自变量，用它指定要圆整的小数位数。
语法是：ceil(参数名或数字, 要圆整的小数位数)floor(参数名或数字, 要圆整的小数位数)如 ceil(2.56,1)=2.6 ceil(-2.56,1)=-2.5floor(2.56,1)=2.5 floor(-2.56,1)=-2.6再例如：A=2.56Ceil(a,1)=2.6 floor(a,1)=2.54.mod()余项函数mod(x,y)的计算方法是：a.先求出x/y的整数部份。
