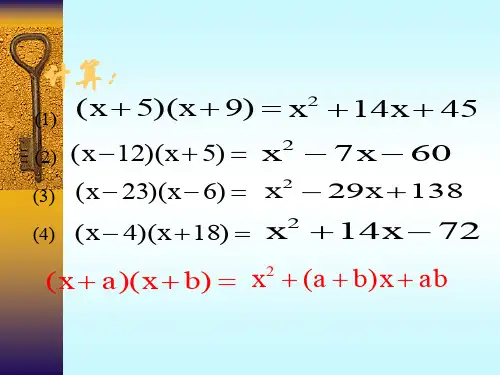十字相乘法课件ppt课件

格式：ppt
大小：391.00 KB
文档页数：18

下载文档原格式

十字相乘法(八年级数学精品课件)

例2、把 y4-7y2-18 分解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式十字相乘法的要领是：“头尾
十字相乘法
“十字相乘法”是乘法公式： (x+a)(x+b)=x2+(a+b)x+ab的反向运算，它适用于分解二次三项式。
例1、把 x2＋6x－7分解因式
十字相乘法（借助十字交叉线分解因式的方法）
例一：
x2 6x 7 (x 7)(x 1)
x

7
x 1
x7x 6x
因式分解：
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解，交叉相乘，求和凑中，观察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式

十字相乘法分解因式ppt课件

(2)(x+y+12)(x+y-4)
(2).(x+y) 2+8(x+y)-48； 14
十字相乘法分解因式（2）
本节课解决两个问题：第一：对形如ax2+bx+c (a≠0)的二次三项式进行因式分解；
第二：对形如ax2+bxy+cy2 (a≠0)的二次三项式进行因式分解；
15
(a1x+c1) (a2x+c2) =ax2+bx+c (a≠0)
1
一、计算：
(1) (x 5)(x 9) x2 14x 45
(2) (x 12)(x 5) x2 7x 60 (3) (x 23)(x 6) x2 29x 138
(4) (x 4)(x 18) x2 14x 72
(x a)(x b) x2 (a b)x ab
2
下列各式是因式分解吗？
x2 14x 45 (x 5)(x 9)
x2 7x 60 (x 12)(x 5)
x2 29x 138 (x 23)(x 6)
x2 14x 72 (x 4)(x 18)
3
x2 px q x2 (a b)x ab (x + a )(x + b)
1
－5
6
－5
2
－1
－1－10=－11
1
1
－5＋6=1
20
练习：将下列各式分解因式
1、 7x 2－13x＋6 答案(7x-6)(x-1) 2、－y 2－4y＋12 答案－ (y＋6)(y－2) 3、 15x2＋7xy－4y 2 答案 (3x－y)(5x＋4y) 4、 x 2－(a＋1) x＋a 答案 (x－1)(x－a)

十字相乘法课件18页PPT

练习：1. x45x236
2. (x2 3 x)2 8 (x2 3 x) 20
思考1：
我们现在所研究的都是二次项系数是1的二次三项式用十字相乘法进行因式分解，那么当二次项的系数不是1，而是其他数字时又该如何进行分解呢？
例如： 3x22x1
分解因式：
（1） x4-3x3 -28x2 (2) 2x2-7x+3 (3) 5x2+6xy-8y2
寻找的两数a和b的符号是如何确定的？
x2pxq(xa)x (b)
当q>0时，a、b（同号），且a、b的符号和p 的符号（相同）.
当q<0时，a、b（异号），且绝对值较大的因数与p的符号（相同 ).
例：分解因式
1. x25xy4y2
2. x45x24
3. (2 xy)2 5 (2 xy) 4
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
十字相乘法课件
16、自己选择的路、跪着也要把它走完。 17、一般情况下)不想三年以后的事，只想现在的事。现在有成就，以后才能更辉煌。
18、敢于向黑暗宣战的人，心里必须充满光明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的人只能引为烧身，只有真正勇敢的人才能所向披靡。
定义：
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。

十字相乘法PPT课件

用十字ቤተ መጻሕፍቲ ባይዱ乘法解一元二次方程
学习目标 : 理解并学会熟练运用十字相乘法进行因
式分解，解一元二次方程 .
学习重点 : 准确应用十字相乘法进行因式分解并进
行适当变式练习。
一、温故知新、自主学习
1．类比：
多位数乘以多位数

125
x +7
× 13
× x -1

3 75
-x -7
③求二次函数y=kx2+x－k+1（k≠0，k 为常数）图象与x轴的交点坐标.
五、自我评价:
1，本节课我主要是学习了： 2，仍感觉有困惑： 3，我认为我这一节课的表现：（A很棒 B一般 C没发挥出来D还需力）. 4，下节课我打算：

=（x+a）（x+b）
其中 p=a+b ，q=ab
二、探究新知、合作交流
1．自主探究：（十字相乘法解一元二次方程） (1)X2+4X+3=0 (2)X2-7X+12=0
(3) X2-7X-30=0
(4)
X2+2X+
3 4
=0
2．合作交流：（十字相乘法法解一元二次方程） (1)3X2-5X+2=0 (2)12y2-5y-2=0
1 2 5
x2 +7x
16 2 5
X2 +6x -7
（x+7 ）（x-1）= X2 +6x -7
过程的对称：
2．计算：
（x+1）(x+2)= （x+3）(x-5)=
3．因式分解： X2-7X+12=

十字相乘ppt课件免费

中等难度实例解析
总结词
中等难度实例涉及稍微复杂的因式分解和乘法运算。
详细描述
例如，将3x^3 - 9x^2 + 6x分解为(x - 2)(3x^2 - 3x + 2)，这个过程需要更深入的理解因式分解的概念，并掌握更复杂的乘法运算。
高难度实例解析
总结词
高难度实例涉及复杂的因式分解和乘法运算，需要较高的数学技巧。
教师可设计多样化的练习题目，让学生充分练习和掌握十字相乘法的技巧，提高解题能力。
教师还应关注学生的反馈和表现，及时给予指导和帮助，促进学生的学习进步。
THANKS FOR WATCHING
感谢您的观看
总结词
求解一元一次方程
详细描述
最后，我们将交叉相乘的结果相加或相减，得到一元一次方程的解。如果一元一次方程有两个解，则原多项式方程也有两个解。
04 实例解析
简单实例解析
总结词
简单实例主要涉及基本的因式分解和乘法运算。
详细描述
例如，将2x^2 - 4x + 2分解为(2x 2)(x - 1)，这个过程需要理解因式分解的概念，并掌握基本的乘法运算。
= b，则这两个数就是方程的两个根。
通过这种方法，我们可以将原方程转化为两个一元一次方程，从而求解出方程的根。
这种方法的关键在于找到合适的 m 和 n，使得它们满足上述条件。
Hale Waihona Puke 原理的数学表达如果 ax^2 + bx + c = 0 是我们要解的一元二次方程，那么我们可以通过以下步骤找到它的根
对学生的建议
学生应熟练掌握十字相乘法的步骤和技巧，通过多练习来提高自己的解题能力。
在学习过程中，学生应积极思考和探索，尝试不同的方法和思路，以培养自己的数学思维和创新能力。

【全版】十字相乘法推荐PPT

x
p
x
q
x2 px＋qx=(p＋q)x pq
十字相乘法：
对于二次三项式的分解因式，
借用一个十字叉帮助我们分解因式，这种方法叫做十字相乘法。
例1 分解因式 x2－6x＋8
解：x 2－6x＋8
x
－2
=(x－2)(x－4) x
－4
－4x－2x=－6x
练习：分解因式 (x－y)2＋(x－y) －6
对于一般地二次三项式ax＋2 bx＋c (a≠0) 此法依然好用。
例2 分解因式 3x2－10x＋3
解：3x 2－10x＋3
x
－3
=(x－3)(3x－1) 3x
－1
－9x－x=－10x
例3 分解因式 5x2－17x－12
解：5x 2－17x－12 5x
＋3
=(5x＋3)(x－4) x
－4
－20x＋3x=－17x
例4 将 2(6x 2＋x) 2－11(6x 2＋x) ＋5 分
在分组分解法中，我们学习了形如 x 2＋(p＋q)x＋pq 的式子的因式分解问题。即：x 2＋(p＋q)x＋pq=(x＋p)(x＋q)
实际在使用此公式时，需要把一次项系数和常数项进行分拆，在试算时，会带来一些困难。
下面介绍的方法，正好解决了这个困难。
即：x 2＋(p＋q)x＋pq=(x＋p)(x＋q)
4例、5 1将0(x2x＋－2)3－xy2－9(2xy＋＋23) x＋＋140y－2 分解因式 5解、：x3－x －(a1＋0x1＋) x3＋a
答案 (2x－1)(5x＋8)
5、 x 2－(a＋1) x＋a 答案 (x－1)(x－a)
例5 将 2x2－3xy－2y2＋3x＋4y－2 分解因式

十字相乘法ppt课件

十字相乘法：利用十字交叉来分解系数，把二次三项式分解因式的方法叫十字相乘法。
2、思考：用十字相乘法进行因式分解的步骤？
步骤：1、竖向分解二次项和常数项； 2、交叉相乘，并把所得的积相加； 3、检验交叉相乘所得的积的和是否
等于一次项。如果等于一次项，则横向书写因式。如果不等于，则考虑重新分解常数项；或者不能用十字相乘法进行分解。
将下列各式用十字相乘法进行因式分解 (1)x2-7x+12 =(x-3)(x-4) (2)x2-4x-12=(x+2)(x-6) (3)x2+8x+12 =(x+2)(x+6) (4)x2-11x-12 =(x+1)(x-12) (5)x2+13x+12=(x+1)(x+12)(6)x2-x-12 =(x+3)(x-4)
1.适用范围：只有当q=ab，且p=a+b时才能用十字相乘法进行分解
2。.掌握方法：拆分常数项，验证一次项。
3.关键步骤是：对常数项的处理，即把常数项分解为两个恰当的常数之积，并使得这两个常数的和等于一次项系数。
4.符号规律：(1)当q>0时，a、b同号，且a、b的符号与p的符号相同；(2)当q<0时，a、b异号，且绝对值较大的因数与p的符号相同.
探究二、分解因式
(1)
=(x+2)(x+3) (2)
=(x-2)(x-3)
(3)
=(x-1)(x+6) (4)
=(x+1)(x-6)
思考：寻找分解常数项所得的两个因数与一次项系数的符号和大小之间有何关系？
(一)符号规律:(1)当常数项为正数时，把它分解为两个同号因数的积，因式的符号与一次项系数的符号相同；

十字相乘法最优课件

小结: 由多项式乘法法则
(x+a)(x+b)=x2+(a+b)x+ab
反过来用就得到一个因式分解的方法
∴x2+(a+b)x+ab=(x+a)(x+b)
x x
a
b
这个方法也称为十字相乘法
小结
只要一个形如x2+mx+n的二次三项式的常数项可以分解成两个有理数相乘,且这两个有理数的和恰好等于一次项的系数,这个多项式就能用十字相乘法分解因式。
想一想:
把下列各式分解因式 (1) x2-4xy-5y2 =(x+y)(x-5y) (2) m2+5mn-6n2 =(m-n)(m+6n) (3) y2-8xy+12x2 =(y-2x)(y-6x) 2 2 (4) a -12ab+36b =(a-6b)2
(5)
b2-7bx2-18x4 =(b+2x2)(b-9x2)
二次项系数不是1的二次三项式
例因式分解：2x2-3x-2 解原式=(x-2)(2x+1)
x 2x
-2
+1
a1a2 x a1c2 a2c1 x c1c2
2
a1 x
c1
a2 x
所以原式可以分解为：a
c2
1 x c1 a2 x c2
因式分解：
6 x 7 xy 5 y
=(m+n-2)(m+n-3)
想一想:
把下列各式分解因式 (3) y2-2y(x-1)-15(x-1)2
=[y+3(x-1)][y-5 (x-1)] =(y+3x-3)(y-5 x+5)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x24x1 2(x_+ _6)_x(__ — _2)__
x21x11 2(x_—_1_)2x(__+_1 _) __
.
9
寻找的两数a和b的符号是如何确定的？
x2 pxq (xa)x(b)
当q>0时，a、b（同号），且a、b的符号和p 的符号（相同）.
当q<0时，a、b（异号），且绝对值较大的因数与p的符号（相同 ).
在日常生活中，如取款，上网等都需要密码，有一种用因式分解法产生的密码，原理是如对于多项式 m4 n4 ，因式分解的结果是 (m n)m (n)m (2n2)，取 m7,n7时，则各个因式的值是
(m n ) 0 ,(m n ) 1,(m 4 2 n 2 ) 9 ,8
于是便可把“01498”作为一个密码，那么对于 x26xy5y2，取 x6,y8时，用上述方法产生的密码可以是_________.
且a _____b（ ; 或a 0,b 0,且a b）（4）当q 0, p 0时，则a _____0,b ______0,
且a _____b（ ; 或a 0,b 0,且a b）
.
11
例2：分解因式
1. x25x4
2. x25xy4y2 3. x45x24
4. (2xy)25(2xy)4
（2）尝试其中的哪两个因数的和恰好等于一次项系数；验证一次项
.
8
例题1：分解式
1. x2 7x12 2. x24x12 3. x2 8x12 4. x211x12
练一练：在下列各式的横线上填入“+”和“—”
号。x27x1 2(x_— _3)_ x (__ — _4)__
x28x1 2(x_+_2)_x(_+_6 _)__
十字相乘法
.
1
课前复习：
1.什么是因式分解？
把一个多项式分解成几个整式的积的形式，叫做把这个多项式因式分解，也叫做把这个多项式分解因式。
因式分解的实质是（“和差化积”）与（整式乘法）是“积化和差”的过程正好（相反）。
2.之前我们都学习了哪些分解因式的方法？
提取公因式法
公式法
.
2
想一想：
那么a和b如何确定呢？满足什么条件呢?
ab q abp
它们的乘积等于常数项，它们的和等于一次项系数。
试一试：将 x24x3 分解因式。
.
7
定义：利用十字交叉线来分解系数,把二次三
项式分解因式的方法叫做十字相乘法。
十字相乘法进行因式分解的关键:
（1）列出常数项分解成两个因数的积的各种可能情况；拆分常数项
(x3)(x4)x27x12
(xa)(xb)x2(ab)xab
等式左边是两个一次二项式（相乘）右边是（二次三项式）
这个过程将（积）的形式，转化成（和差）的形式，进行的是（整式乘法）运算。
.
5
(x3)(x4)= (x3)(x4)= (x3)(x4)=
x27x12 x2 x12 x2 x12
（2）A和B中至少有一个为0，即A=0或B=0。
请结合上面的结论，运用十字相乘法解下列一元二次方程：
1）. x27x60 2）. x27x12
.
14
.
15
想一想：
在日常生活中，如取款，上网等都需要密码，有一种用因式分解法产生的密码，方便记忆，原理是如对于多项式 m4 n4 ，因式分解的结果是 (m n)m (n)m (2n2)，取m7,n7时，则各个因式的值是
.
3
计算下列各题：
(x3)(x4)x27x12 (x3)(x4)x2 x12 (x3)(x4)x2 x12 (x3)(x4)x27x12 问：你有什么快速计算类似多项式的方法吗？
(xa)(xb)x2(ab)xab
.
4
(x3)(x4)x2 7x12 (x3)(x4)x2 x12 (x3)(x4)x2 x12
练习：1. x45x236 2. (x23x)28(x23x)20
.
12
思考2：
我们现在所研究的都是二次项系数是1的二次三项式用十字相乘法进行因式分解，那么当二次项的系数不是1，而是其他数字时又该如何进行分解呢？
例如：3x2 2x1
.
13
课外拓展:
若 AB0 ，下面两个结论对吗？（1）A和B同时都为0，即A=0且B=0；
(m n ) 0 ,(m n ) 1,(m 4 2 n 2 ) 9 ,8
于是便可把“01498”作为一个密码，那么对于 x26xy5y2，取 x6,y8时，
用上述方法产生的密码可以是___1_4_4_6___.
.
16
思考3：
是不是所有的二次三项式都可以用十字相乘法进行因式分解呢？如果不是，那满足什么条件的二次三项式可以用十字相乘法进行因式分解呢？
(x3)(x4)= x27x12
x2pxq (xa)(xb)= x2(ab)xab
等式左边是（二次三项式），二次项的系数是（1）
等式右边是两个一次二项式（相乘），整个等式从左到右将（和差）的形式转化成（积）的形式，
进行的是（因式分解）。
x 2 p q x x 2 (a b )x a (x b a )x (b )
.
17
作业：
1. 练习册9.15 1——4题， 5题（1）——（4）
2.练习纸。
.
18
.
10
思考1:
若二次三项式能找到两数a、b使它分解为 x2p xq(xa)x(b)，则：
（1）当q 0, p 0时，则a______0,b______0 （2）当q 0, p 0时，则a _____0,b ______0 （3）当q 0, p 0时，则a _____0,b ______0,