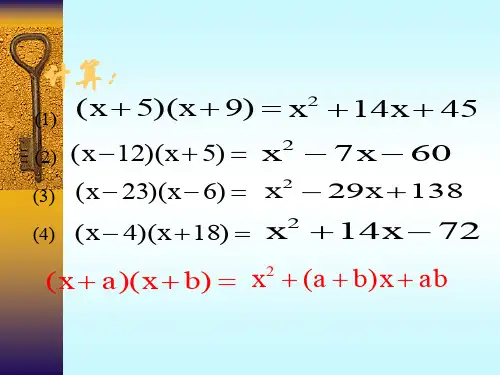当前位置：文档之家 › 十字相乘法-PPT课件

十字相乘法-PPT课件

  • 格式：ppt
  • 大小：1.08 MB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

十字相乘法(八年级数学精品课件)

十字相乘法(八年级数学精品课件)

例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是：“头尾
十字相乘法
“十字相乘法”是乘法公式： (x+a)(x+b)=x2+(a+b)x+ab的反 向运算，它适用于分解二次三 项式。
例1、把 x2＋6x－7分解因式
十字相乘法（借助十字交叉线分解因式的方法）
例一：
x2 6x 7 (x 7)(x 1)
x

7
x 1
x7x 6x
因式分解：
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解，交叉相乘，求和凑中，观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式

十字相乘法课件

十字相乘法课件
(x+a)(x+b)=x2+(a+b)x+ab X2+(a+b)x+ab=(x+a)(x+b) 二次三项式x2+(a+b)x+ab的特点: 1.二次项的系数是1. 2.常数项是两个数之积. 3.一次项系数是常数项的两个因数之和.
二次项系数为1的二次三项式x2+px+q,如果能够 把常数项q分解成两个因数a`b的积,并且a+b等 于一次项系数p,那么它就可以分解因式: 即x2+px+q= X2+(a+b)x+ab=(x+a)(x+b)
cd=(-2)x(-5)=10=C=原式中的常数项
解:原式=(x-2)(3x-5)
1 -2
3
-5
(2)
2
6x2-11x-10
-5
3
2
解:原式=(2x-5)(3x+2)
2 (11)3x -7x+2 2 (12)2x -x-3
(13)5x2+13x+6 2 (14)6x -2x-8 (15)10x2-15x+5 2 (16)3x +11x+10
2-5x-14 X
-14=(-1)×14 -14=1×(-14) -14=(-2)×7
x2+(a+b)x+ab=(x+a)(x+b)
a+b=-5,ab=-14
谁是a? 谁是b?
-14=2×(-7)
a= -7 b= 2
解:原式=(x-7)(x+2)
(1)
x2-5x+6
x2+(a+b)x+ab=(x+a)(x+b) a+b=-5 ab=6 a=-3 b=-2 解:原式=(x-3)(x-2)

十字相乘法课件

十字相乘法课件


(m 2)(m 4)



试一试，填空：
(1) x 4 x 3 ( x __ 3)( x __1) + +
2
(2) x 2 x 3 ( x __ 3)( x __1) +
2
(3) x x 20 ( x 4)( x 5)
2
(4) y 16 y 15 ( y 1)(y 15)
例1:分解因式 x 2 - 10 x + 21
1 1 －3 －7
x - 3 x - 7
1 (7) 1 (3) 10
注意:处理系数时要带符号起处理
所以:原式= ( x - 3 ) ( x - 7 )
例2:
(1) x2 + x - 2 (2) x2 - 2x - 15
分析(1) x2 + x - 2的两次项系数是 1,常数项-2=(-1) × 2,一次项系数 1=(-1)+2,得:
2
(6) x x 30
2
(7) x 7 x 6
2
(8) x 4 x 12
2
练一练 2 （1） x 9 x 20
（2） （3） （4） （5）
x 3x 18
2
2
x 3x 28 2 x 6x 8 2 m m 42
跳到思考
(x+a)(x+b) = x2+(a+b)x+ab 看谁算得快：
x2+3x+2 = 2. (x-2)(x-1) =X2-3x+2
1. (x+2)(x+1) 3. (x-2)(x+1) 4. (x+2)(x-1) 5. (x+2)(x+3) 6. (x-2)(x-3) 7. (x-2)(x+3) 8. (x+2)(x-3)

十字相乘法因式分解课件

十字相乘法因式分解课件

步骤二：寻找两个数，它们的乘积等于常数项
总结词
确定两个数的乘积与常数项相等
详细描述
在找到两个数的和与一次项的系数相等后，我们需要找到这两个数的乘积等于常数项的数。例如，在因式分解 “x^2 + 5x + 6”，我们需要找到两个数，它们的乘积为6。
步骤三：验证结果
总结词
验证分解结果的正确性
详细描述
十字相乘法因式分解
目录
CONTENTS
• 引言 • 十字相乘法的基本原理 • 十字相乘法的步骤 • 十字相乘法的应用 • 练习与挑战
01 引言
什么是十字相乘法
十字相乘法是一种数学方法，用于将 多项式因式分解为两个一次因式的乘 积。
该方法通过将多项式的常数项和一次 项系数分别分解为两个数的乘积，然 后交叉相乘得到一次项系数，从而找 到因式分解的两个一次因式。
代数式的化简
代数式化简的定义
将一个代数式通过变形、合并同 类项等方式简化。
十字相乘法的应用
在代数式化简过程中，有时需要通 过因式分解来简化代数式，而十字 相乘法是因式分解的一种常用方法 。
代数式化简的步骤
首先将代数式整理为易于因式分解 的形式，然后使用十字相乘法进行 因式分解，最后将因式分解后的代 数式进行简化。
在这个例子中，我们通过观察二次多项式的系数，找到两个数6和-1，它们的和 等于二次项的系数5，并且它们的乘积等于常数项-6，从而实现了因式分解。
03 十字相乘法的步骤
步骤一
总结词
确定两个数的和与一次项的系数相等
详细描述
在因式分解过程中，首先需要找到两个数，它们的和应等于一次项的系数。例 如，在因式分解“x^2 + 5x + 6”，我们需要找到两个数，它们的和为5。

因式分解——十字相乘法 —初中数学课件PPT

因式分解——十字相乘法 —初中数学课件PPT
如果一个多项式适当分组，使分组 后各组之间有公因式或可应用公式，那 么这个多项式就可以用分组的方法分解 因式。
练一 练
mx+my-nx-ny ① ② ③④
①②，③④两组，得（mx+my）-（nx+ny）
解1：原式= （mx+my）-（nx+ny） =m(x+y)-n(x+y) =(x+y)(m-n)
x2+px+q= x2+(a+b)x+ab= (x+a)(x+b)
x
a
x
ax +
b
bx = (a+b)x
步骤： ①竖分二次项与常数项； ②交叉相乘，和相加； ③检验确定，横写因式．
顺口溜： 竖分常数交叉验， 横写因式不能乱．
将下列各式因式分解： 1．x2+8x+12= (x+2)(x+6) 2．x2-11x-12= (x-12)(x+1) 3．x2-7x+12= (x-3)(x-4) 4．x2-4x-12= (x-6)(x+2) 5．x2+13x+12= (x+1)(x+12) 6．x2-x-12= (x-4)(x+3)
（4）(x-1)(x+2)(x-3)(x+4)+24 解：(x-1)(x+2)(x-3)(x+4)+24
= 9a4-(4a2-4a+1)
= (x2+x-2)(x2+x-12)+24
= 9a4-(2a-1) 2 = (3a2+2a-1)(3a2-2a+1)
= (x2+x) 2-14(x2+x)+48 = (x2+x-2+px+q进行因式分解， 应重点掌握以下三个问题：

十字相乘法课件18页PPT

十字相乘法课件18页PPT
练习：1. x45x236
2. (x2 3 x)2 8 (x2 3 x) 20
思考1：
我们现在所研究的都是二次项系数是1的二 次三项式用十字相乘法进行因式分解，那 么当二次项的系数不是1，而是其他数字时 又该如何进行分解呢？
例如： 3x22x1
分解因式：
（1） x4-3x3 -28x2 (2) 2x2-7x+3 (3) 5x2+6xy-8y2
寻找的两数a和b的符号是如何确定的？
x2pxq(xa)x (b)
当q>0时，a、b（ 同号 ），且a、b的符号和p 的符号（ 相同 ）.
当q<0时，a、b（ 异号 ），且绝对值较大的因 数与p的符号（ 相同 ).
例：分解因式
1. x25xy4y2
2. x45x24
3. (2 xy)2 5 (2 xy) 4
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
十字相乘法课件
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌。
18、敢于向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
定义：
利用十字交叉线来分解系数,把二次三 项式分解因式的方法叫做十字相乘法。

十字相乘法PPT课件

十字相乘法PPT课件
用十字ቤተ መጻሕፍቲ ባይዱ乘法解一元二次方程
学习目标 : 理解并学会熟练运用十字相乘法进行因
式分解，解一元二次方程 .
学习重点 : 准确应用十字相乘法进行因式分解并进
行适当变式练习。
一、温故知新、自主学习
1．类比：
多位数乘以多位 数

125
x +7
× 13
× x -1

3 75
-x -7
③求二次函数y=kx2+x－k+1（k≠0，k 为常数）图象与x轴的交点坐标.
五、自我评价:
1，本节课我主要是学习了： 2，仍感觉有困惑 ： 3，我认为我这一节课的表现： （A很棒 B一般 C没发挥出来D还需力）. 4，下节课我打算：

=（x+a）（x+b）
其中 p=a+b ，q=ab
二、探究新知、合作交流
1．自主探究：（十字相乘法解一元二次方程） (1)X2+4X+3=0 (2)X2-7X+12=0
(3) X2-7X-30=0
(4)
X2+2X+
3 4
=0
2．合作交流：（十字相乘法法解一元二次方程） (1)3X2-5X+2=0 (2)12y2-5y-2=0
1 2 5
x2 +7x
16 2 5
X2 +6x -7
（x+7 ）（x-1）= X2 +6x -7
过程的对称：
2．计算：
（x+1）(x+2)= （x+3）(x-5)=
3．因式分解： X2-7X+12=

十字相乘ppt课件免费

十字相乘ppt课件免费

中等难度实例解析
总结词
中等难度实例涉及稍微复杂的因式分 解和乘法运算。
详细描述
例如，将3x^3 - 9x^2 + 6x分解为(x - 2)(3x^2 - 3x + 2)，这个过程需要 更深入的理解因式分解的概念，并掌 握更复杂的乘法运算。
高难度实例解析
总结词
高难度实例涉及复杂的因式分解和乘法运算，需要较高的数学技巧。
教师可设计多样化的练习题目，让学生充分练习 和掌握十字相乘法的技巧，提高解题能力。
教师还应关注学生的反馈和表现，及时给予指导 和帮助，促进学生的学习进步。
THANKS FOR WATCHING
感谢您的观看
总结词
求解一元一次方程
详细描述
最后，我们将交叉相乘的结果相加或相减，得到一元一次方程的解。如果一元一次方程有两个解，则原多项式方 程也有两个解。
04 实例解析
简单实例解析
总结词
简单实例主要涉及基本的因式分解和 乘法运算。
详细描述
例如，将2x^2 - 4x + 2分解为(2x 2)(x - 1)，这个过程需要理解因式分解 的概念，并掌握基本的乘法运算。
= b，则这两个数就是方程的两个根。
通过这种方法，我们可以将原方程转化为两个一元一 次方程，从而求解出方程的根。
这种方法的关键在于找到合适的 m 和 n，使得它们满 足上述条件。
Hale Waihona Puke 原理的数学表达如果 ax^2 + bx + c = 0 是我们要解的 一元二次方程，那么我们可以通过以下 步骤找到它的根
对学生的建议
学生应熟练掌握十字相乘法的步骤和技巧，通过多练习来提高自己的解题能力。
在学习过程中，学生应积极思考和探索，尝试不同的方法和思路，以培养自己的数 学思维和创新能力。

十字相乘法最优课件

十字相乘法最优课件

小结: 由多项式乘法法则
(x+a)(x+b)=x2+(a+b)x+ab
反过来用就得到一个因式分解的方法
∴x2+(a+b)x+ab=(x+a)(x+b)
x x
a
b
这个方法也称为十字相乘法
小结
只要一个形如x2+mx+n的二次三项式的常 数项可以分解成两个有理数相乘,且这两个有理 数的和恰好等于一次项的系数,这个多项式就能 用十字相乘法分解因式。
想一想:
把下列各式分解因式 (1) x2-4xy-5y2 =(x+y)(x-5y) (2) m2+5mn-6n2 =(m-n)(m+6n) (3) y2-8xy+12x2 =(y-2x)(y-6x) 2 2 (4) a -12ab+36b =(a-6b)2
(5)
b2-7bx2-18x4 =(b+2x2)(b-9x2)
二次项系数不是1的二次三项式
例 因式分解：2x2-3x-2 解原式=(x-2)(2x+1)
x 2x
-2
+1
a1a2 x a1c2 a2c1 x c1c2
2
a1 x
c1
a2 x
所以原式可以分解为：a
c2
1 x c1 a2 x c2
因式分解：
6 x 7 xy 5 y
=(m+n-2)(m+n-3)
想一想:
把下列各式分解因式 (3) y2-2y(x-1)-15(x-1)2
=[y+3(x-1)][y-5 (x-1)] =(y+3x-3)(y-5 x+5)

十字相乘法Microsoft PowerPoint 演示文稿

十字相乘法Microsoft PowerPoint 演示文稿

智慧 & 分享 ☞ 对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b) 进行因式分解,应重点掌握以下问题:
1.适用范围:只有当q=ab,且p=a+b时才能用十字 相乘法进行分解。 2.掌握方法:拆分常数项,验证一次项. 3.符号规律：
当q>0时,a、b同号,且a、b的符号与p的符号相同; 当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
(x+a)(x+b) =x2+(a+b)x+ab
(x+a)(x+b) = x2+(a+b)x+ab
1. (x+2)(xபைடு நூலகம்1) 2. (x+2)(x-1) 3. (x-2)(x+1) 4. (x-2)(x-1) 5. (x+2)(x+3) 6. (x+2)(x-3) 7. (x-2)(x+3) 8. (x-2)(x-3)
x
1 1 x 7x 6x
x - 7x = - 6x
x

7

①竖分二次项与常数项
或
7
②交叉相乘,和相加 ③检验确定,横写因式
顺口溜：竖分常数 交叉验，横写因式 不能乱。
方法 & 理解 ☞
把下列各式分解因式： 当常数项是正数时,分解的 2 1. x -5x+6 =(x-2)(x-3) 两个数必 同 号,即都为正 或 2. x2-5x-6 =(x- 6)(x+1) 都为负 ,且两数之和等于一 3. x2+5x-6 =(x+6)(x-1) 次项系数.当常数项是负数 时,分解的两个数必为异 号, 2 4. x +5x+6=(x+2)(x+3) 且两数之和仍得 一次项系数 .
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、若x2+mx+20能在实数 范围内分解因式，则m的 整数值有几个？
2、分解因式2x2+5x+2
⑴ )x2-16x+39 ⑵-x2-2x+15 (3) ax2-ax-6a (4)x4-3x2+2 (5) (x－y)2 ＋(x－y) －6
用十字相乘法进行因式分解：
1.x2-x- 6 = (x+2)(x-3) 11.x2+13x+12= (x+1)(x+12)
练习1：分解因式
(1) x2+9x+8
(2) x2-9x+8
规律:常数项是正数时,它分解
成两个同___号_因数，它们的符号与
_一__次__项__系__数____相同。
例2：分解因式
(1)x2+5x-6
(2)x2-5x-6
规律：常数项是负数时，它分解成两个
_异__号__因数，_绝__对__值__较___大__的__数的符号与
一次项系数符号相同。
练习2：分解因式
(1) x2+2x-8 (2) x2-2x-8
练习பைடு நூலகம்：分解因式
(1) x2-4x+4
能用完全平方公式进行因式分解的多项 式，利用十字相乘法也可以分解因式。
(2) -x2-3x+4
二次项系数为负时，先提负号再分解。
(3) 3x2-9x+6
有公因式时，先提公因式再分解。
用我们已经学过的方法 你会分解x2+5x+6 吗？
我说你猜
两数之积6，两数之和5，求两数。 两数之积6，两数之和-5，求两数。 两数之积-6，两数之和1，求两数。 两数之积-6，两数之和-1，求两数。
计算下列各题
(1)(x+2)(x+3)= (2)(x+5)(x-4)= (3)(x-4)(x+1)= (4) (x-3)(x-5)=
2.x2+2x-15= (x-3)(x+5) 12.x2-11x-12= (x-12)(x+1)
3.x2-3x-10= (x+2)(x-5) 4.x2-9x+20= (x-5)(x-4) 5.x2-3x-28= (x-7)(x+4) 6.x2-2x-8= (x+2)(x-4) 7.x2-4x+3= (x-1)(x-3) 8.x2+7x+12= (x+3)(x+4) 9.x2+5x+6= (x+2)(x+3)
10.x2+4x-21=(x-3)(x+7)
13.y2+9y-36= (y+12)(y-3) 14.y2-11y-60= (y+4)(y-15) 15.y2+19y+48= (y+16)(y+3) 16.y2+y-110= (y+11)(y-10) 17.y2-16y+39= (y-13)(y-3) 18.y2+18y+56= (y+14)(y+4)
2+3 2×3
x2+ 5x + 6
5+(-4) 5×(-4)
x2+ 1x - 20
(-4)+1 (-4)×1
x2- 3x - 4
(-3)+(-5) (-3)×(-5)
x2- 8x + 15
(5) (x+p)(x+q)= x2+(p+q)x +pq
例1:分解因式
(1)x2+5x+6 (2)x2-5x+6