当前位置：文档之家 › 实验一 零输入响应零状态响应

实验一 零输入响应零状态响应

  • 格式：doc
  • 大小：6.33 MB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

信号与系统实验——零输入响应、零状态响应和全响应实验

信号与系统实验——零输入响应、零状态响应和全响应实验

实验三信号与系统实验
1. 零输入响应、零状态响应和全响应实验
1.1实验目的
(1)掌握零输入相应、零状态响应和全响应的意义。

(2)了解零输入响应、零状态响应和全响应三者之前的关系。

1.2实验步骤和结果
(1)零状态响应：在零输入、零状态及全响应单元格，将IN端接地，按下按钮S给电容放电以保证系统没有初始状态。

将直流信号源的开关拨到直流档，调节电位器使其输出+4V的直流信号。

将此信号接入IN端，按下按钮S，用示波器测量OUT端波形，大概画出所测量波形并记录表中各时刻对应的幅值。

图一零状态响应Array
(2)零输入响应：保持直流信号接入到IN端，按下按钮S，用示波器观察输出信号，待系统稳定后断开按钮。

此时电容充满电，系统拥有初态。

将直流信号从IN端断开，接IN端接地，这样系统便没有激励，按下按钮S，用示波器测量OUT端波形，大概画出所测的波形，
并记录表中各时刻对应的幅值。

图二零输入响应
(3)全响应：利用上述方法重新对电容充电，充电后保持直流信号接入到IN端，按下按钮S，用示波器测量OUT端波形，大概画出对应时刻的波形并记录表中各时刻对应的幅值。

图三全响应
3.总结
结合上面三个表格，对应每个表格各时刻的值，虽然读数有一定的偏差，但是基本上满足关系式：全响应=零输入响应+零状态响应。

从这个关系式可以得出零状态响应加上零输入响应得到的就是全响应。

零输入响应是一种系统的初态，零状态响应是没有初态的系统加入激励后产生的响应后的系统。

即拥有初态的系统，再给予其一个激励，产生的响应就
是全响应。

零输入响应和零状态响应

零输入响应和零状态响应

计算方法
利用系统的传递函数和初始条 件进行计算。
通过求解常微分方程或差分方 程ห้องสมุดไป่ตู้找到系统的零输入响应。
在MATLAB/Simulink等仿真软 件中，可以通过设置系统的初 始状态来模拟零输入响应。
02 零状态响应
定义
零状态响应：是指在系统无输入 信号的情况下，系统对初始状态
产生的响应。
描述了系统在没有输入信号作用 时，其内部状态的变化情况。
零状态响应完全取决于系统本身 的特性，与输入信号无关。
产生原因
系统内部存在储能元件（如电容、电 感），当输入信号为零时，储能元件 的能量不会立即消失，而是会以某种 形式继续存在并产生响应。
系统参数（如电阻、电感、电容等） 发生变化，导致系统内部状态发生变 化，从而产生零状态响应。
计算方法
根据系统的传递函数 和初始状态进行计算。
针对复杂系统和多尺度问题，发展基于零输入响应和零状态响应的跨学科 解决方案，促进各领域之间的交流与合作。
探索零输入响应和零状态响应在可持续发展、环境保护、公共安全等领域 的潜在应用价值，为社会发展和人类福祉做出贡献。
技术创新
开发高效、稳定的零输入响应和零状态响应算 法，提高计算效率和精度，降低计算成本。
零状态响应
零状态响应描述的是系统在外部输入作用下的输出变化。通过研究零状态响应， 可以了解系统对不同类型输入的响应特性，进而设计出更好的控制系统。
系统建模与仿真
零输入响应
在系统建模与仿真中，零输入响应用 于描述系统的内部动态特性。通过分 析零输入响应，可以深入了解系统的 内部工作原理和稳定性。
零状态响应
零状态响应用于描述系统对外部输入 的响应特性。通过研究零状态响应， 可以预测系统在不同输入条件下的行 为表现，有助于优化系统的设计和控 制。

零输入响应和零状态响应

零输入响应和零状态响应

齐次解
X
第 14
页
两种分解方式的区别：
1、 自由响应与零输入响应的系数各不相同
c c 与 i
xi 不相同
c i 由初始状态和激励共同确定
c xi 由初始状态确定
2、 自由响应包含了零输入响应和零状态响应中的齐次解
对于系统响应还有一种分解方式，即瞬态响应和稳态响应。所谓瞬态响应指
t 时，响应趋于零的那部分响应分量；而稳态响应指 t
(Cte-t
)
3
d dt
(Cte-t
)
2(Cte-t
)
e-t
特解 yp (t) t et
零状态响应： yzs (t) C1et C2e2t t et
由起始状态导出初始条件
y(0 ) 0 y '(0 ) 0
y(0 ) 0 y '(0 ) 0
y(0 ) C1 y '(0 ) C1
r1(t) rzi (t) rzs (t) 2e3t sin(2t) u(t)
r2 (t) rzi (t) 2rzs (t) [e3t 2sin(2t)]u(t)
X
四.对系统线性的进一步认识
第 17
页
解得 rzi (t) 3e3tu(t) rzs (t) [e3t sin(2t)]u(t)
零输入响应： 没有外加激励信号的作用，只由起始状态（起始时刻系 统储能）所产生的响应。
零状态响应： 不考虑原始时刻系统储能的作用（起始状态等于 零），由系统的外加激励信号产生的响应。
X
二．起始状态与激励源的等效转换
第 4
页
在一定条件下，激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。

零输入响应和零状态响应举例

零输入响应和零状态响应举例
零输入响应和零状态响应举例
例：描述某系统的微分方程为
y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t) 已知y(0-)=2，y’(0-)=0，f(t)=ε(t)。求该系统的零输入
响应和零状态响应。
解：（1）零输入响应yzi(t) 激励为0 ，故yzi(t)满足
yzi”(t) + 3yzi’(t) + 2yzi(t) = 0
■
第1页
（2）零状态响应yzs(t) 满足
yzs”(t) + 3yzs’(t) + 2yzs(t) = 2δ(t) + 6ε(t) 并有 yzs(0-) = yzs’(0-) = 0
由于上式等号右端含有δ(t)，故yzs”(t)含有δ(t)，从而 yzs’(t)跃变，即yzs’(0+)≠yzs’(0-)，而yzs(t)在t = 0连续，
即yzs(0+) = yzs(0-ห้องสมุดไป่ตู้ = 0，积分得
[yzs’(0+)- yzs’(0-)]+ 3[yzs(0+)- yzs(0-)]+002 yzs(t)dt2600 (t)dt
因此，yzs’(0+)= 2 + yzs’(0-
对)t=>20时，有 yzs”(t) + 3yzs’(t) + 2yzs(t) = 6
yzi(0+)= yzi(0-)= y(0-)=2
yzi’(0+)= yzi’(0-)= y’(0-)=0
该齐次方程的特征根为–1， – 2，故
yzi(t) = Czi1e –t + Czi2e –2t
代入初始值并解得系数为Czi1=4 ,Czi2= – 2 ，代入得

零输入响应与零状态响应

零输入响应与零状态响应

零输⼊响应与零状态响应1.零输⼊响应与零状态响应在Matlab中，lsim函数还可以对带有⾮零起始状态的LTI系统进⾏仿真，使⽤⽅法为y=lsim(sys,u,t,x0)，其中sys表⽰LTI系统，⽮量u和t分别表⽰激励信号的抽样值和抽样时间，⽮量x0表⽰该系统的初始状态，返回值y是系统响应值。

如果只有起始状态⽽没有激励信号，或者令激励信号为0，则得到零输⼊响应。

如果既有初始状态也有激励信号，则得到完全响应。

请注意lsim函数只能对⽤状态⽅程描述的LTI系统仿真⾮零起始状态响应，函数ss（对传递函数描述的LTI系统将失效，函数tf）。

例2.5 给定如图所⽰电路，t<0时S处于1的位置⽽且已经达到稳态，将其看做起始状态，当t=0时，S由1转向2.分别求t>0时i(t)的零状态响应和零输⼊响应。

图2.1 例2.4 电路图解：由所⽰电路写出回路⽅程和结点⽅程分别得到状态⽅程和输出⽅程：下⾯将⽤两种⽅法计算完全响应。

第⼀种⽅法：⾸先仿真2V电压e作⽤⾜够长时间（10s）后系统进⼊稳态，从⽽得到稳态值x0，再以该值作为初始值仿真4V电压e作⽤下的输出rf，即是系统的完全响应，为充分掌握lsim函数的使⽤⽅法，还仿真了系统的零状态响应rzs和零输⼊响应rzi。

第⼆种⽅法：构造⼀个激励信号，先保持2V⾜够长时间再跳变为4V，然后即可以零初始状态⼀次仿真得到系统的完全响应r1。

对应程序如下：C=1;L=1/4;R1=1;R2=3/2;A=[-1/R1/C,-1/C;1/L,-R2/L];B=[1/R1/C;0];C=[-1/R1,0];D=[1/R1];sys=ss(A,B,C,D); %建⽴LTI 系统systn=[-10:0.01:-0.01]'; %⽣成-10s 到-0.01s 的抽样时间，间隔为0.01sen=2*(tn<0); %⽣成机理信号的抽样值e(t)=2[rn tn xn]=lsim(sys,en,tn); %仿真t<0时的输出信号x0=xn(length(en),:); %x0记录了初始状态的值t=[0:0.01:10]';e=4*(t>=0); %⽣成激励信号的抽样值e(t)=4ezi=0*(t>=0); %⽣成零输⼊信号的抽样值e(t)=0rzs=lsim(sys,e,t); %仿真零状态响应rzi=lsim(sys,ezi,t,x0); %仿真零输⼊响应rf=lsim(sys,e,t,x0); %仿真完全响应r1=lsim(sys,[en;e],[tn;t]); %⽤另⼀种⽅法仿真完全响应2. 冲激响应与阶跃响应如果分别⽤冲激信号和阶跃信号作激励，lsim 函数可仿真出冲激响应和阶跃响应。

零输入响应和零状态响应

零输入响应和零状态响应
r3(t) rzi (t) rzs (t t0 ) 3e3tu(t) [e3(tt0 ) sin(2t 2t0 )]u(t t0 )
r4 (t) 2rzi (t) 0.5rzs (t) 2 3e3tu(t) 0.5 e3t sin(2t) u(t)
X
各种系统响应定义
第 3
页
自由响应： 也称固有响应，由系统本身特性决定，与外加激励形 式无关。对应于齐次解。
强迫响应： 形式取决于外加激励。对应于特解。
暂态响应： 是指激励信号接入一段时间内，完全响应中暂时出现的 有关成分，随着时间t 增加，它将消失。
稳态响应： 由完全响应中减去暂态响应分量即得稳态响应分量。
由起始条件
y(0 ) C1 C2 1

y
'(0 )

C1

2C2

2
得零输入响应为
yzi (t ) 4et 3e2t , t 0
X
三.求解
第 9
页
零状态响应
系统零状态响应，是在激励作用下求系统方程的非齐次解，由
状态值 vC (0 ) iL (0 ) 为零决定的初始值求出待定系数。
r1(t) rzi (t) rzs (t) 2e3t sin(2t) u(t)
r2 (t) rzi (t) 2rzs (t) [e3t 2sin(2t)]u(t)
X
第
四.对系统线性的进一步认识
17 页
解得 rzi (t) 3e3tu(t) rzs (t) [e3t sin(2t)]u(t)
自由响应 强迫响应
n
n

c eit xi

电路实验上机 RLC串联电路的零输入响应与零状态响应


零输入响应的模式完全由其微分方程的特征方程的两个特征根：
R R 1 ( )2 p1 2L 2L LC p R ( R )2 1 1 2L 2L LC
(1)当 过阻尼情况。 (2)当 为临界阻尼情况。 (3)当 欠阻尼情况。
，则 P 12 为两个不相等的实根，电路的动态响应为非振荡性的，称为
，则 P 12 为两个相等的负实根，电路的动态响应仍为非振荡性的，称
，则 P 12 为两个不相等的共轭根，电路的动态响应为振荡性的，称为
2、二阶电路的阶跃响应 二阶电路对于阶跃函数输入的零状态响应称为二阶电路的阶跃响应。 定义任一时刻 起始的单位阶跃函数为
当电路的激励为单位阶跃
或
A 时，相当于电路在 t=0 时电压值为 1V 的直
实验报告成绩：
评阅教师签字： 年 月 日
电力工程学院二〇〇七年制
一、实验目的
1、了解 Multisim9 程序的使用过程，掌握其基本操作。 2、加深对 RLC 串联电路的零输入和阶跃响应实验的理解与认识。 3、学会利用 Multisim9 程序对 RLC 串联电路的的零输入响应和阶跃响应进行分析，模 拟波形生成。
六、心得体会
通过本次实验，我基本学会了如何使用 Multicap 软件设计电路，并通过仿真得到 实验数据，这样所得的实验数据误差小，同时可供选择的电路元件多，还可以拟合实验 数据曲线，极大的方便了我们的实验过程，降低了实验成本。 同时， 通过亲自上机操作， 对于 RLC 串联电路的零输入响应和阶跃响应及其波形随 时间变化趋势也有了进一步了解，理论知识和实践相结合，利用课上学到的理论知识， 设计电路，然后通过仿真去检验分析出来的理论的真确性。操作简单易行。

零输入响应和零状态响应举例

▲ ■ 第 2页yzs(t) 满足
yzs”(t) + 3yzs’(t) + 2yzs(t) = 2δ(t) + 6ε(t) 并有 yzs(0-) = yzs’(0-) = 0 由于上式等号右端含有δ(t)，故yzs”(t)含有δ(t)，从而 yzs’(t)跃变，即yzs’(0+)≠yzs’(0-)，而yzs(t)在t = 0连续，即 yzs(0+) = yzs(0-) = 0，积分得 0 0 [yzs’(0+)- yzs’(0-)]+ 3[yzs(0+)- yzs(0-)]+2 0 y zs (t ) d t 2 60 (t ) d t
因此，yzs’(0+)= 2 + yzs’(0-)=2 对t>0时，有 yzs”(t) + 3yzs’(t) + 2yzs(t) = 6 不难求得其齐次解为Czs1e-t + Czs2e-2t，其特解为常数3， 于是有 yzs(t)=Czs1e-t + Czs2e-2t + 3 代入初始值求得 yzs(t)= – 4e-t + e-2t + 3 ，t≥0
1零输入响应yzi2t代入初始状态值得czi12e2t3yzs2yzs带入方程比较等号两端t项的系数得a22零状态响应yzszszs3yzs2yzs2t其特解为常数3
零输入响应和零状态响应举例
例：描述某系统的微分方程为 y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t) 已知y(0-)=2，y’(0-)=0，f(t)=ε(t)。求该系统的零输入 响应和零状态响应。 解：（1）零输入响应yzi(t) 激励为0 ，故yzi(t)满足 yzi”(t) + 3yzi’(t) + 2yzi(t) = 0 yzi(0+)= yzi(0-)= y(0-)=2 yzi’(0+)= yzi’(0-)= y’(0-)=0 该齐次方程的特征根为–1， – 2，故 yzi(t) = Czi1e –t + Czi2e –2t 代入初始值并解得系数为Czi1=4 ,Czi2= – 2 ，代入得 yzi(t) = 4e –t – 2e –2t ,t > 0

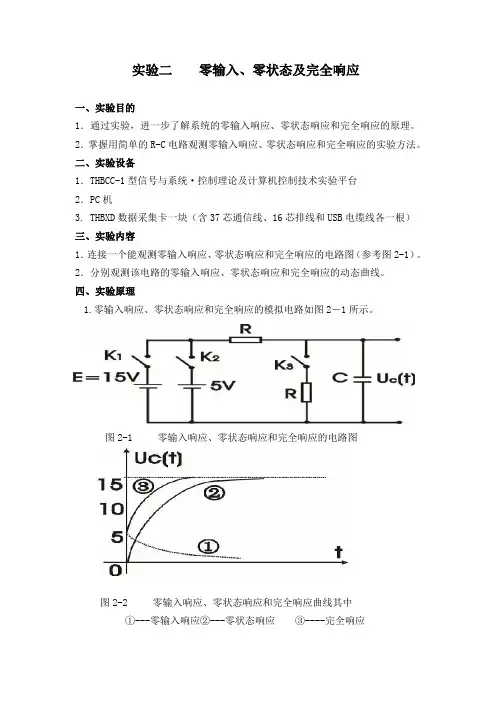
零输入、零状态及完全响应

实验二零输入、零状态及完全响应一、实验目的1．通过实验，进一步了解系统的零输入响应、零状态响应和完全响应的原理。

2．掌握用简单的R-C电路观测零输入响应、零状态响应和完全响应的实验方法。

二、实验设备1．THBCC-1型信号与系统·控制理论及计算机控制技术实验平台2．PC机3. THBXD数据采集卡一块（含37芯通信线、16芯排线和USB电缆线各一根）三、实验内容1．连接一个能观测零输入响应、零状态响应和完全响应的电路图（参考图2-1）。

2．分别观测该电路的零输入响应、零状态响应和完全响应的动态曲线。

四、实验原理1.零输入响应、零状态响应和完全响应的模拟电路如图2－1所示。

图2-1零输入响应、零状态响应和完全响应的电路图图2-2 零输入响应、零状态响应和完全响应曲线其中①---零输入响应②---零状态响应③----完全响应式(3)等号右方的第二项为零输入响应，即由初始条件激励下的输出响应；第一项为零状态响应，它描述了初始条件为零（Uc（0）=0）时，电路在输入E=15V 作用下的输出响应，显然它们之和为电路的完全响应，图2-2所示的曲线表示这三种的响应过程。

五、实验步骤1.实验准备1.1 将“阶跃信号发生器”的输出端接至实验台上“输入响应、零状态响应和完全响应”单元的“+2V”输入端，调节“阶跃型号发生器”正输出的“RP1”电位器，让阶跃输出为“2V”;1.2 将“直流稳压电源”的“+5V”接至“零输入响应、零状态响应和完全响应”单元的“+5V”输入端。

1.3 将“零输入、零状态和完全响应”单元的输出端与“数据采集接口单元”的AD1通道相连。

2. 零输入响应将S1短接到2处，S2短接到1处，使+2V直流电源对电容C充电，当充电完毕后，将S2接到2处，用“THBCC-1”软件上的“虚拟示波器”观察并记录Uc(t)的变化。

零输入响应2．零状态响应先将S2短接到2处，使电容两端的电压放电完毕，将S1接到1处，S2接到1处，用虚拟示波器观察并记5V直流电向电容的充电过程。

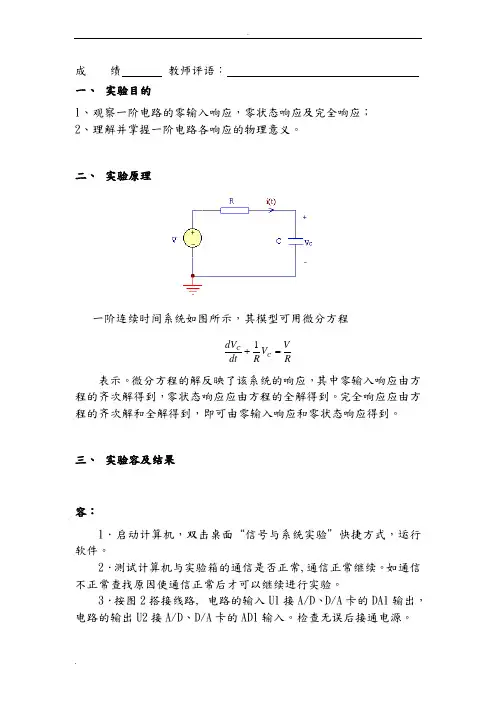
试验箱实验一一阶电路的零输入响应、零状态响应及完全响应

成 绩 教师评语： 一、 实验目的1、观察一阶电路的零输入响应，零状态响应及完全响应；2、理解并掌握一阶电路各响应的物理意义。

二、 实验原理一阶连续时间系统如图所示，其模型可用微分方程RVV R dt dV C C =+1 表示。

微分方程的解反映了该系统的响应，其中零输入响应由方程的齐次解得到，零状态响应应由方程的全解得到。

完全响应应由方程的齐次解和全解得到，即可由零输入响应和零状态响应得到。

三、 实验容及结果 容：1．启动计算机，双击桌面“信号与系统实验”快捷方式，运行软件。

2．测试计算机与实验箱的通信是否正常,通信正常继续。

如通信不正常查找原因使通信正常后才可以继续进行实验。

3．按图2搭接线路, 电路的输入U1接A/D 、D/A 卡的DA1输出，电路的输出U2接A/D 、D/A 卡的AD1输入。

检查无误后接通电源。

图2 一阶电路响应实验电路零状态响应4．在实验项目的下拉列表中选择实验三[三、一阶电路的零状态响应、零输入响应和完全响应], 鼠标单击按钮，弹出实验课题参数设置对话框，选择零状态响应，在参数框中输入目的电压值及有关采样的参数，点击确认在观察窗口观测系统响应曲线。

5．记录实验波形。

零输入响应6．在实验项目的下拉列表中选择实验三[三、一阶电路的零状态响应、零输入响应和完全响应], 鼠标单击按钮，弹出实验课题参数设置对话框，选择零输入响应，在参数框中输入电平一的电压值和保持时间及有关采样的参数，电平二的电压值默认为0，点击确认在观察窗口观测系统响应曲线。

7．记录实验波形。

完全响应8．在实验项目的下拉列表中选择实验三[三、一阶电路的零状态响应、零输入响应和完全响应], 鼠标单击按钮，弹出实验课题参数设置对话框，选择完全响应，在参数框中输入电平一和电平二的电压值及其保持时间及有关采样的参数，点击确认在观察窗口观测系统响应曲线9．记录实验波形。

结果：零状态响应电平1:1000mv电平1:500mv电平1:100mv零输入响应电平1:500mv、电平2:500mv保持：500ms电平1:1000mv、电平2:600mv保持：600ms完全响应电平1:3000mv 电平2:800ms保持：-3000mv 保持：800ms电平1:1000mv 电平2:900ms 保持：-3000mv 保持：900ms电平1:3000mv 电平2:300ms 保持：-1000mv 保持：500ms四．实验结果分析：（观察波形与理论分析波形差异的原因） 理论上该电路完全响应为求解微分方程RVV R dt dV C C =+1 （1） 零输入响应特征方程为 r+1/（RC ）=0 解得特征根为 r=-1/（RC ） 所以零输入响应为（2） 零状态响应为求零状态响应，必须先求得电路的冲击响应h （t ）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

郑玉明
090706329
09电科3班
实验一 零输入响应零状态响应
一、实验目的
1、掌握电路的零输入响应。

2、掌握电路的零状态响应。

3、学会电路的零状态响应与零输入响应的观察方法。

二、实验内容
1、观察零输入响应的过程。

2、观察零状态响应的过程。

三、实验仪器
1、信号与系统实验箱一台（主板）。

2、系统时域与频域分析模块一块。

3、20MHz 示波器一台。

四、实验原理
1、零输入响应与零状态响应： 零输入响应：没有外加激励的作用，只有起始状态（起始时刻系统储能）所产生的响应。

零状态响应：不考虑起始时刻系统储能的作用（起始状态等于零）。

2、典型电路分析：
电路的响应一般可分解为零输入响应和零状态响应。

首先考察一个实例：在下图中由RC 组成一电路，电容两端有起始电压Vc(0-),激励源为e(t)。

图2-1-1 RC 电路则系统响应－电容两端电压：
1
()0
1()(0)()t
t
t RC
RC
C c V t e
V e e d RC -τ=-+ττ⎰ 上式中第一项称之为零输入响应，与输入激励无关，零输入响应(0)t
RC
c e V -是以初始电
压值开始，以指数规律进行衰减。

第二项与起始储能无关，只与输入激励有关，被称为零状态响应。

在不同的输入信号下，电路会表征出不同的响应。

五、实验步骤
1、把系统时域与频域分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。

2、系统的零输入响应特性观察
（1）接通主板上的电源，同时按下此模块上两个电源开关，将“时域抽样定理”模块中的抽样脉冲信号（SK1000用于选择频段，“频率调节”用于在频段内的频率调节，“脉宽调节”用于脉冲宽度的调节，以下实验都可改变以上的参数进行相关的操作），通过导线引入到“零输入零状态响应”的输入端。

（2）用示波器的两个探头，一个接输入脉冲信号作同步，一个用于观察输出信号的波形，当脉冲进入低电平阶段时，相当于此时激励去掉，即在低电平时所观察到的波形即为零输入信号。

（3）改变本实验的开关SK900的位置，观察到的是不同情况下的零输入响应，进行相应的比较
3、系统的零状态响应特性观察
（1）观察的方法与上述相同，不过当脉冲进入高电平阶段时，相当于此时加上激励，即此时零状态响应应在脉冲的高电平进行。

（2）改变本实验的开关SK900的位置，观察到的是不同系统下的零输入响应，进行相应的比较。

六、零输入和零状态的输出波形
1.sk900----上
a.sk1000----低
b.sk1000---中
c.sk1000---高
2.sk900----下
a.sk1000----低
b.sk1000---中
c.sk1000---高。