高一数学竞赛选拔考试

高级中学高一数学竞赛班选拔考试试题第二卷（第二轮 考试时间60分钟，满分100分）班级 姓名 得分一、选择题（每题６分，36分）1．集合｛0,1，2,2004｝的子集的个数是 （ ）（A ）16 （B ）15 （C ）8 （D ）7 ２．乘积22221111(1)(1)(1)(1)23910---- 等于( ). (A)125 (B)21 (C)2011 (D)107 3 ．某公司从2001年起每人的年工资主要由三个项目组成并按下表规定实施：若该公司某职工在2005年将得到的住房补贴与医疗费之和超过基础工资的25%，到2005年底这位职工的工龄至少是（ ） （A ）2年（B ）3年（C ）4年（D ）5年4.若F(11x x-+)=x 则下列等式正确的是（ ）. （A ）F(-2-x)=-1-F(x)（B ）F(-x)=11x x+-（C ）F(x -1)=F(x)（D ）F （F （x ））=-x 5．已知c b a 、、是实数，条件0:=abc p ；条件0:=a q ，则p 是q 的（ ）(A)必要不充分条件(B)充分不必要条件(C)充分必要条件(D)不充分也不必要条件6．已知四边形ABCD 在映射f ：),(y x →)2,1(+-y x 作用下的象集为四边形D C B A ''''。

四边形ABCD 的面积等于6，则四边形D C B A ''''的面积等于（ ）A ．9B ．26C ．34D ．6 二、填空题（每题5分，25分）7．如果}66{}42,3,2,1{}2,{22--=-a a a a ，则a 的值是 。

8. Let f be a function such that 22))((2)()(y f x f y x f +=+ for any real numbers x and y , and 0)1(≠f , then (2005)f is equal to _____________.9．甲、乙、丙、丁、戊五位同学，看五本不同的书A 、B 、C 、D 、E ，每人至少要读一本书，但不能重复读同一本书，甲、乙、丙、丁分别读了2、2、3、5本书，A 、B 、C 、D 分别被读了1、1、2、4次。

智才艺州攀枝花市创界学校2021年上学期桂阳三中高一数学竞赛班选拔考试试卷一、选择题〔每一小题5分，45分〕1、.假设非空集合A={x |2a+1≤x ≤3a 5}，B={x|3≤x ≤22}，那么能使A 〔A B 〕成立的所有a 的集合是() (A){a|1≤a ≤9}(B){a|6≤a ≤9}(C){a|a ≤9}(D)Φ 2、定义A*B ，B*C ，C*D ，D*B 分别对应以下列图形那么以下列图形中可以表示A*D ，A*C 的分别是.A ．〔1〕、〔2〕B ．〔1〕、〔3〕C ．〔2〕、〔4〕D ．〔3〕、〔4〕3．有理数x 、y 、z 两两不等，那么,,x y y z z xy z z x x y ------中负数的个数是() 4．的解的个数为方程xx 22=() A.0B.1 C5.假设F(11xx -+)=x 那么以下等式正确的选项是〔 〕.〔A 〕F(-2-x)=-1-F(x)〔B 〕F(-x)=11xx +-〔C 〕F(x-1)=F(x)〔D 〕F 〔F 〔x 〕〕=-x442+-=x x y 的定义域为[]b a ,(a<b),值域为[]b a ,,那么这样的闭区间[]b a ,是下面的()A.[]4,0 B.[]4,1 C.[]3,1 D.[]4,37、一椭圆形地块，打算分A 、B 、C 、D 四个区域栽种欣赏植物，要求同一区域种同一种植物，相邻的两块种不〔1〕 〔2〕〔3〕 〔4〕〔1〕 〔2〕 〔3〕 〔4〕A B CD同的植物，现有4种不同的植物 可供选择，那么有〔〕种栽种方案. A.60B.68 C8．四边形ABCD 在映射f：),(y x →)2,1(+-y x 作用下的象集为四边形D C B A ''''。

四边形ABCD 的面积等于6，那么四边形D C B A ''''的面积等于〔〕A ．9B ．26C ．34D ．69.甲乙两人轮流在黑板上写下不超过10的正整数，规定制止在黑板上写已经写过的数的数，最后不能写的为失败者，假设甲写第一个，那么，甲写数字〔〕时有必胜的策略 A ．10B.9 C二、填空题〔每一小题5分，一共25分〕10、函数1,()0x f x x ⎧=⎨⎩为有理数，，为无理数.0,()x g x x ⎧=⎨⎩为有理数，1，为无理数.当x R∈时，()()_______,f g x =()()_______.g f x =11、甲、乙、丙、丁、戊五位同学，看五本不同的书A 、B 、C 、D 、E ，每人至少要读一本书，但不能重复读同一本书，甲、乙、丙、丁分别读了2、2、3、5本书，A 、B 、C 、D 分别被读了1、1、2、4次。

数学竞赛高一试题及答案一、选择题（每题5分，共10分）1. 已知函数\( f(x) = 2x^2 - 3x + 1 \)，求\( f(-1) \)的值。

A. 4B. 6C. 8D. 102. 一个圆的半径为5，求其面积。

A. 25πB. 50πC. 75πD. 100π二、填空题（每题5分，共10分）3. 已知\( a \)、\( b \)、\( c \)为三角形的三边长，且\( a^2 + b^2 = c^2 \)，这个三角形是________。

4. 将\( 1 \)、\( 2 \)、\( 3 \)三个数字排列成三位数，所有可能的组合数是________。

三、解答题（每题15分，共30分）5. 已知数列\( \{a_n\} \)满足\( a_1 = 1 \)，\( a_{n+1} = a_n + 2n \)，求\( a_5 \)。

6. 一个直角三角形的斜边长为\( 5 \)，一条直角边长为\( 3 \)，求另一条直角边长。

四、证明题（每题15分，共30分）7. 证明：对于任意正整数\( n \)，\( 1^3 + 2^3 + ... + n^3 = (1 + 2 + ... + n)^2 \)。

8. 证明：若\( a \)、\( b \)、\( c \)是三角形的三边长，且\( a^2 + b^2 = c^2 \)，则这个三角形是直角三角形。

五、综合题（每题15分，共20分）9. 一个工厂计划在一年内生产\( x \)个产品，已知生产每个产品的成本是\( 10 \)元，销售每个产品的价格是\( 20 \)元。

如果工厂希望获得的利润不少于\( 10000 \)元，求\( x \)的最小值。

10. 已知函数\( g(x) = x^3 - 6x^2 + 11x - 6 \)，求\( g(x) \)的极值点。

答案：一、选择题1. 答案：B. 6（计算方法：\( f(-1) = 2(-1)^2 - 3(-1) + 1 = 2 + 3 + 1 = 6 \)）2. 答案：B. 50π（计算方法：圆面积公式为\( πr^2 \)，代入\( r = 5 \)）二、填空题3. 答案：直角三角形4. 答案：6（排列组合方法：\( 3 \times 2 \times 1 = 6 \)）三、解答题5. 答案：\( a_5 = 1 + 2(1) + 2(2) + 2(3) + 2(4) = 1 + 2 + 4 +6 + 8 = 21 \)6. 答案：根据勾股定理，另一条直角边长为\( 4 \)（计算方法：\( 5^2 - 3^2 = 4^2 \)）四、证明题7. 证明：根据等差数列求和公式，\( 1 + 2 + ... + n =\frac{n(n+1)}{2} \)，立方后得到\( \left(\frac{n(n+1)}{2}\right)^2 \)，展开后即为\( 1^3 + 2^3 + ... + n^3 \)。

世界青少年奥林匹克数学竞赛（YMO）（中国区）选拔赛全国总决赛高中一年级试卷（无答案）第 2 页秘密★启用前第九届世界青少年奥林匹克数学竞赛（中国区）选拔赛全国总决赛试卷注意事项：1、考生按要求用黑色、蓝色圆珠笔或钢笔在密封线内填好考生的相关信息。

2、考试时间120分钟。

3、本试卷共6页，满分100分。

4、不得在答卷或答题卡上做任何标记。

5、考生超出答题区域答题将不得分。

6、考生在考试期间不得作弊，否则试卷记零分处理。

高中一年级试题一、 选择题。

以下每题的四个选项中只有一个是正确的，请将表示正确答案的英文字母写在每题后面的 括号内。

每题3分，共24分。

1、角α=cos 2019°在（ ）A.第一象限B.第二象限C.第三象限D.第四象限2、设命题甲：x =＞2或y ≤1；命题乙：x ≥3且y ＜2.则“命题甲不成立”是 “命题乙不成立”的（ ）A.充分不必要条件.B.必要不充分条件.C.充要条件.D.非充分非必要条件. 3、The minimum of |x |+|x -1|+|x -2|+……+|x -2019| is （ ）A.1003²B.1004²C.2019²D.2019²4、若关于x 的二次函数y =x ²-3mx +3的图像与端点在（21，25）和（3,5）的线段只有一个交点，则m 的值可能是（ ）A. 25B. 1C. 21 D. 31 5、在下边的每个空格中填入一个正数，使每一行方格总 分 阅卷人 ∕∕∕∕∕∕∕∕∕∕〇∕∕∕∕∕∕∕〇∕∕∕∕∕∕ ∕∕密 〇 封 〇 装 〇 订 〇 线 ∕∕∕∕∕∕〇∕第 3 页第 4 页6、如图所示的程序框图的输出结果为 。

开始 K=1 S=0 K ＞2019？S=S+1/k （k+2） 输出SK=k+27、已知梯形ABCD 中，AB=8，BC=4，CD=5，BC ⊥AB ，AB∥CD ，动点P 由B 点出发，沿BC ，CD ，DA 运动到A 点。

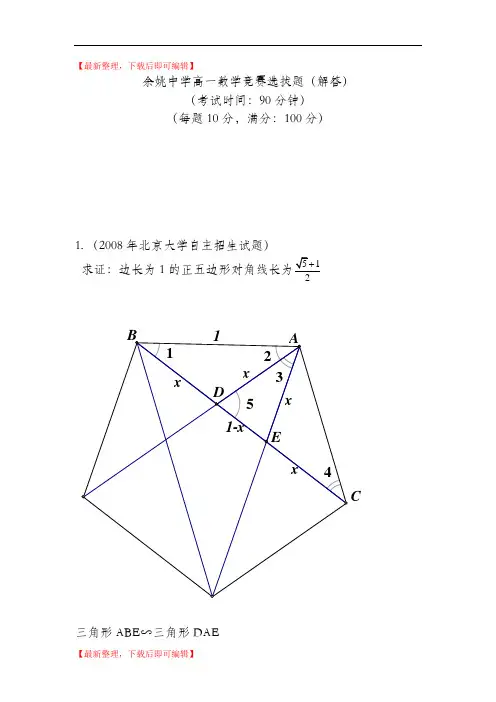
【最新整理，下载后即可编辑】2222RNBNCRNXNO+⋅=+=，①同理22RMAMCMO+⋅=. ②因为A，C，D，P四点共圆，所以MPMDMAMC⋅=⋅，③因为Q，D，C，B四点共圆，所以NQNDNBNC⋅=⋅，④由①，②，③，④得MPMDNQNDMONO⋅-⋅=-22)()(DPMDMDDQNDND+-+=M)(22DP MD DQ ND MD ND ⋅-⋅+-=, 所以， OD MN ⊥⇔2222MD ND MO NO -=-DP MD DQ ND ⋅=⋅⇔⇔P ,Q ,M ,N 四点共圆.3．（第一届“希望杯”全国邀请赛试题）求函数7210626174)(2234++++++=x x x x x x x f 在区间[-1，1]上的值域。

解：1726472)(22-+++++=x x x x x f 。

值域为]3215,15[。

4. （2000年北京市中学生数学竞赛）f(x)是定义在R 上的函数，对任意的x ∈R ，都有f(x+3) ≤f(x)+3和f(x+2) ≥f(x)+2，设g(x)=f(x)-x ，（1）求证g(x)是周期函数；（2）如果f(998)=1002，求f(2000)的值。

解：本例的难度显然又有增加，主要是难以具体化。

只能在抽象的层面来解决问题 （1）g(x)=f(x)-x ， 可得g(x+2)=f(x+2)-x-2， g(x+3)=f(x+3)-x-3，再以f(x+3) ≤f(x)+3和f(x+2) ≥f(x)+2代换，可得x x f x x f x g -=--+≥+)(22)()2(，① x x f x x f x g -=--+≤+)(33)()3(，②由①可得g(x+4) ≥f(x+2)-x-2 ≥f(x)+2-x-2=f(x)-x ，g(x+6) ≥f(x+2)-x-2≥f(x)-x 。

③由②可得g(x+6) ≤f(x+3)-x-3≤f(x)-x ，④由③、④知g(x+6)=f(x)-x=g(x)。

高一数学竞赛试题及答案一、选择题（每题5分，共30分）1. 若a，b，c是三角形的三边长，且满足a² + b² = c²，那么这个三角形是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定2. 函数f(x) = 2x³ - 3x² + 1在区间[-1,2]上的最大值是：A. 1B. 7C. 9D. 无法确定3. 已知集合A = {1, 2, 3}，B = {2, 3, 4}，求A∪B的元素个数：A. 3B. 4C. 5D. 64. 等差数列的首项a₁ = 3，公差d = 2，第10项a₁₀的值是：A. 23B. 25C. 27D. 295. 圆的方程为(x - 2)² + (y - 3)² = 9，圆心到直线x + 2y - 7= 0的距离是：A. 2B. 3C. 4D. 56. 已知函数y = |x| + 1的图像与直线y = kx平行，那么k的值是：A. 1B. -1C. 0D. 无法确定二、填空题（每题4分，共20分）7. 若二次函数y = ax² + bx + c的顶点坐标为(-1, -4)，则a =_______。

8. 已知等比数列的首项为2，公比为3，第5项的值为 _______。

9. 一个正六边形的内角和为 _______。

10. 若直线y = 2x + b与曲线y = x² - 3x相切，则b = _______。

11. 圆的方程为x² + y² = 25，圆上一点P(4,3)到圆心的距离是_______。

三、解答题（每题25分，共50分）12. 已知直线l₁：2x - 3y + 6 = 0与直线l₂：x + y - 2 = 0相交于点M，求点M的坐标。

13. 已知函数f(x) = x³ - 3x + 2，求证：对于任意的x > 0，都有f(x) > x。

高一竞赛选拔试题及答案一、选择题（每题3分，共30分）1. 下列关于函数的描述中，不正确的是（）。

A. 函数是数学中的一种关系，其中每个输入值都对应一个输出值。

B. 函数可以表示为一个表格、图形或公式。

C. 函数的值域是所有可能的输入值的集合。

D. 函数的图像是函数值域和定义域的图形表示。

答案：C2. 如果一个数列是等差数列，那么它的相邻两项之差是一个常数。

这个常数被称为（）。

A. 公比B. 公差C. 等比数列D. 等差数列答案：B3. 在几何学中，一个点到一个平面的最短距离是（）。

A. 垂直于平面的线段B. 任意一条线段C. 点到平面上任意一点的距离D. 点到平面上最近点的距离答案：A4. 以下哪个选项是复数的代数形式？（）A. a + biB. a - biC. a + bD. a - b答案：A5. 以下哪个函数是奇函数？（）A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x答案：B6. 以下哪个选项是二项式定理的展开式？（）A. (a + b)^n = Σ (n choose k) * a^(n-k) * b^kB. (a + b)^n = Σ (n choose k) * a^k * b^(n-k)C. (a + b)^n = Σ (n choose k) * a^(n-k) * b^kD. (a + b)^n = Σ (n choose k) * a^k * b^(n-k)答案：B7. 以下哪个选项是三角函数的基本恒等式？（）A. sin^2(x) + cos^2(x) = 1B. sin(x) + cos(x) = 1C. sin(x) * cos(x) = 1D. sin(x) / cos(x) = tan(x)答案：A8. 以下哪个选项是指数函数的一般形式？（）A. f(x) = a^xB. f(x) = log_a(x)C. f(x) = x^aD. f(x) = a * x答案：A9. 以下哪个选项是双曲线的标准方程？（）A. (x^2) / a^2 - (y^2) / b^2 = 1B. (x^2) / a^2 + (y^2) / b^2 = 1C. (y^2) / a^2 - (x^2) / b^2 = 1D. (y^2) / a^2 + (x^2) / b^2 = 1答案：A10. 以下哪个选项是向量的点积定义？（）A. a · b = |a| * |b| * cos(θ)B. a · b = |a| * |b| * sin(θ)C. a · b = |a| * |b| * tan(θ)D. a · b = |a| * |b| * cot(θ)答案：A二、填空题（每题4分，共20分）11. 如果一个函数f(x)在区间[a, b]上连续，并且f(a) = f(b)，那么根据罗尔定理，存在至少一个c属于(a, b)，使得f'(c) =________。

重点中学高一数学竞赛班选拔考试试卷1.{}{}0,1A x x =⊆,用列举法表示集合A=___________。

2.新高一某班的50名学生中，参加数学竞赛辅导的有22人，参加物理竞赛辅导的有20人，参加化学竞赛辅导的有19人，既参加数学又参加物理的有15人，既参加数学又参加化学的有12人，既参加物理又参加化学的有10人，三科都没参加的有20人，则三科都参加的有_____________人。

3．在小于100的正整数n 中，能使分数1(332)(41)n n ++化为有限小数的n 的所有可能值为___________。

4．在一个圆形时钟的表面，OA 表示秒针，OB 表示分针（O 为两针的旋转中心）。

若现在时间恰好是12点整，则经过_______秒后，OAB ∆面积第一次达到最大。

（用分数表示） 5.已知a 、b 、c 为整数，且2006,2005a b c a +=-=，若a b <，则a b c ++的最大值为________. b=2013-a>a 则a<1006.5 a 最大为1006 c=2005+a 所以a+b+c=2006+2005+a=a+4011所以最大值是1006+4011=50176．如果两个一元二次方程20x x m ++=与210mx x ++=都有两个不相等的实数根，并且其中有一个公共的实根0x ，那么0x =_________。

7．如果一个两位数5x 与一个三位数3yz 的积是29400，那么，x y z ++=____。

29400/400>73, 29400/300=98x 只能为7或8或929400/75=392只有这个是整数。

所以x+y+z=7+9+2=18因为29400=75*392所以x=7、y=9,z=2所以x+y+z=7+9+2=188．一名模型赛车手遥控一辆赛车。

先前进1米，然后原地逆时针方向旋转角0(0180)αα<<，被称为一次操作。

江西省萍乡市芦溪中学高一数学竞赛选拔试题一、选择题（本大题共10小题,每小题6分,共计60分）1.设集合M=⎭⎬⎫⎩⎨⎧∈+==⎭⎬⎫⎩⎨⎧∈+=Z k k x x N Z k k x x ,)214(|,,)412(|ππ,则有A M=NB M NC N MD M ∩N=φ2.集合M 由正整数的平方组成，即{}1,4,9,16,25,...M =，若对某集合中的任意两个元素进行某种运算，运算结果仍在此集合中，则称此集合对该运算是封闭的. M 对下列运算封闭的是A. 加法B. 减法C. 乘法D. 除法3.已知集合A={x |0≤x ≤4},集合B={y|0≤y ≤2},则下列从集合A 到集合B 的对应不是映射是A.x y x f 21:=→B.x y x f 31:=→C.x y x f 32:=→ D.281:x y x f =→4.函数)2,(21-∞-+=在x ax y 上为增函数,则实数a 的取值范围是A.21->a B.21>a C.21<a D.21-<a5.已知函数0)(,)1,1(213)(00=--+=x f x a ax x f 使得上存在在,则a 的取值范围是A.511<<-aB.51>a C.1-<a 或51>a D.1-<a6. 对于任意实数x ，若不等式34(0)x x a a -+->>恒成立，则实数a 应满足A. 01a <<B. 01a <≤C. 1a >D. 1a ≥7. 等差数列{}n a 、{}n b 的前n 项的和分别为n S 、n T ，且3323n n S n T n -=+，则66a b =A. 32 B. 1C. 65D. 27238.已知二次函数)1(,0)(),0()(2-<>+-=m f m f a a x x x f 则若的值是 A.正数 B.负数 C.零 D.符号与a 值有关9.定义A*B ，B*C（1） （2） （3） （4）那么下列图形中可以表示A*D ，A*C 的分别是A ．（1）、（2）B ．（1）、（3）C ．（2）、（4）D ．（3）、（4） 10.设函数2log ()a y ax x a =++的定义域是R 时,a 的取值范围为集合M;它的值域是R 时,a 的取值范围为集合N,则下列的表达式中正确的是 A. M ⊇N B.MN R = C.M N =∅ D.M N =二、填空题（本大题共5小题,每小题6分,共30分）11.函数|1|122---=x x x y 的单调增区间为 . 12.函数)2(,3)2(,2)(235-=++++=f f bx x ax x x f 则若的值等于 . 13.二次函数122++=ax ax y 在区间[－3,2]上最大值为4,则a 等于 . 14．已知函数1,()0x f x x ⎧=⎨⎩为有理数，，为无理数.0,()x g x x ⎧=⎨⎩为有理数，1，为无理数.当x R ∈时， ()()_______,f g x =()()_______.g f x =15．设{}n a 是集合{}220,,s t s t s t Z +≤<∈且中所有的数从小到大排成的数列，则550________,_____.a a ==三、解答题（本大题4小题,共60分） 16.（本题满分12分）已知函数.2222)(xx xx x f --+-= （1）求函数的定义域和值域； （2）试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB 恰好与y 轴垂直,若存在,求出A,B 两点的坐标；若不存在,说明理由并加以证明.（1） （2） （3） （4）17.（本题满分12分） 已知不等式||2|3|x x >+ ①12322≥+-+x x x ②0122<-+mx x ③（1）若同时满足①②的x 的值也满足不等式③,求实数m 的取值范围. （2）若满足不等式③的x 的值至少满足①②中的一个,求实数m 的取值范围.18.（本题满分18分）已知一次函数b ax x f +=)(与二次函数且满足,)(2c b a c bx ax x g >>++=).,,(0R c b a c b a ∈=++ （1）求证：函数)()(x g y x f y ==与的图象有两个不同的交点A,B ； （2）设A 1,B 1是A,B 两点在x 轴上的射影,求线段A 1B 1长的取值范围； （3）求证：当3-≤x 时,)()(x g x f <恒成立.19. （本题满分18分）已知数列{a n }的前n 项和S n 满足S n －S n －2=3,23,1),3()21(211-==≥--S S n n 且求数列{a n }的通项公式.[参考答案] 一、选择题：1.B2.C3.C4.D5.C6.A7.C8.A9.C 10.C 二、填空题：11. （－∞，0），]1,0( 12. 9 13. －3或3/8 14. 1,0 15. 10, 1040 三、解答题：16. 解：（1）由014022≠+≠+-xx x 得所以)(x f 的定义域{}R x x ∈|----------------2分由011:,04,1142222>-+>-+=⇒+-=--y y y y y xx xx x x 所以而所以}11|{)(<<-y y x f 的值域----------------------------------4分 （2）不存在，因为)(x f y =在R 上为增函数.------------- - ------6分 证明：任设x 1<x 2，则)14)(14(4414141414)()(2121221121++-=+--+-=-x x x x x x x x x f x f -------8分 因为x 1<x 2，y=4x在R 上为增函数，所以044,442121<-<x x x x 即而)()(,0)()(,014,14212121x f x f x f x f x x <<->++即所以所以y=f(x)在R 上为增函数.---------------------- ----------------10分 则f(x)的图象上不存在两个不同的点A ，B 使直线AB 恰好与y 轴垂直.--12分 17. 解：①的解集为A={x|－1<x <3}，②的解集为B={4210|≤<<≤x x x 或}}41|{},3210|{≤<-=⋃<<<≤=⋂x x B A x x x B A 或--------4分1）要满足题意，则方程2x 2+m x －1=0的一根小于0，大于等于3.-------- 5分 设f(x)= 2x 2+m x －1，则317)3(0)0(-≤⇒⎩⎨⎧≤<m f f --------------------7分 2）要满足题意，则方程2x 2+m x －1=0的两根应在区间[－1，4]上.-----8分设f(x)= 2x 2+m x －1，则143144/10)4(0)1(≤≤-⇒⎪⎪⎩⎪⎪⎨⎧<-<->∆≥≥-m m f f ------------12分18. 解:（1）由0)(,)()(22=-+--++=+=b c x b a ax c bx ax x g b ax x f 得和----2分则2()4,,0(,,).a b ac a b c a b c a b c R ∆=+->>++=∈又且0,0,0,a c ><∴∆>则----------------------------------4分 ∴函数)()(x g y x f y ==与的图象有两个不同的交点A,B ； ---6分（2）由,/)(,/)(2121a b c x x a b a x x -=-=+则4)2(||||22111--==-=a cx x B A ----------------------------------------9分又因为2/1/2).,,(0,-<<-∈=++>>a c R c b a c b a c b a 则且);32,2/3(||11∈B A ---------------------------------------------12分（3）设b c x b a ax x f x g x F -+--=-=)()()()(2的两根为21,x x 满足21x x <，则3212<-x x ，------------------------------14分又y=F(x )的对称轴为：,02>-=a b a x 于是321<--x a ba ，∴a ba x ab a 23231-<<--<-，由此得：当3-≤x 时，,21a ba x x -<<--------------------16分又)2,()(,0a ba x F a --∞>在知上为单调递减函数，于是，,0)()(1=<x F x F 即当)()(,3x g x f x <-≤时恒成立-----------------------18分19. 解:先考虑偶数项有：1212222)21(3)21(3---⋅-=-⋅=-n n n n S S 32324222)21(3)21(3----⋅-=-⋅=-n n n n S S……….)21(3)21(23324⋅-=-⋅=-S S ).1()21(2])41(2121[4411)41(21213]21)21()21()21[(3])21()21()21[(312332123321222≥+-=⋅--=--⋅-=++++-=+++-=∴-----n S S n n n n n n n n同理考虑奇数项有：.)21(3)21(3221212n n n n S S ⋅=-=--- 22223212)21(3)21(3----⋅=-⋅=-n n n n S S……….)21(3)21(32213⋅=-⋅=-S S.1).1()21(34))21(2()21(2).1()21(34))21(2()21(2).1()21(2])21()21()21[(31112122122221222121222222112==≥⋅+-=--+-=-=≥⋅-=+---=-=∴≥-=++++=∴----++-+S a n S S a n S S a n S S n n n n n n n n n n n n n n n n综合可得⎪⎪⎩⎪⎪⎨⎧⋅+-⋅-=--.,)21(34,,)21(3411为偶数为奇数n n a n n n。

高一年级竞赛考试数学试卷一、选择题（每小题5分，共60分）1. 已知集合{}{}332,6,4,2,0<∈==xN x B A ，则集合A B 的子集个数为( )A.4B. 6C. 7D. 8 2、函数lg(1)1x y x +=-的定义域是（ ）A . (1,)B . [1,)C . (1,1)(1,)D . [1,1)(1,)-+∞-+∞-+∞-+∞3．已知直线a x y l 2:1+-=与直线2)2(:22+-=x a y l 平行，则a 的值为( ) A ．3± B. 1± C. 1 D. 1-4.设a ， b 是两条不同的直线， α， β是两个不同的平面，下列命题中正确的是（ ） A. 若//αβ， a α⊂， b β⊂，则//a b B. 若//a α， b β⊥，且αβ⊥，则//a b C. 若a α⊥， //a b ， //b β，则αβ⊥ D. 若a b ⊥， a α⊂， b β⊂，则αβ⊥5. 已知一个空间几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ），可得这个几 何体的体积是( )A ．4 cm 3B ．5 cm 3C ．6 cm 3D ．7 cm 36．半径为R 的半圆做成一个圆锥面（无重叠），则由它围成的圆锥的体积为（ ） A 33R B 33R C 35R D 35R 7.已知⎩⎨⎧≥<+-=1log 14)13()(x xx a x a x f a 是),(+∞-∞上的减函数，那么a 的取值范围是（ ）A ．)1,0( B. )31,0( C.)31,71[ D.)1,71[ 8.圆心为)1 , 1(-M 且与直线027=+-y x 相切的圆的方程为( ) A ．2)1()1(22=++-y x B ．2)1()1(22=-++y x C ．100)1()1(22=++-y x D ．100)1()1(22=-++y x9. 已知三棱锥P ABC -的三条棱PA ,PB ,PC 长分别是3、4、5，三条棱PA ,PB ,PC 两两垂直，且该棱锥4个顶点都在同一球面上，则这个球的表面积是 ( ) A ．25π B.50π C. 125π D.都不对10.已知函数)(x f 的图象向右平移a (0>a )个单位后关于直线1+=a x 对称，当112>>x x 时，[]0)()()(1212<--x x x f x f 恒成立，设)21(-=f a ，)2(f b =)，)(e f c =，则a ，b ，c 的大小关系为 （ ）A.b a c >>B.c a b >>C.b c a >>D. a b c >>11. 四面体S ABC -中，各个侧面都是边长为a 的正三角形，,E F 分别是SC 和AB 的中 点，则异面直线EF 与SA 所成的角等于（ ）A ．090B ．060C ．045D ．03012. 已知偶函数)(x f 的定义域为}{0≠∈x R x x 且， ⎪⎩⎪⎨⎧>-≤<-=-2),2(2120,12)(1x x f x x f x ，则函数)1(log )(4)(7+-=x x f x g 的零点个数为（ ）．A. B. C. D. 二、填空题 (每小题5分，共20分)13.已知函数()f x 是R 上的奇函数，且0x >时，()1f x x =+,则当0x <时，()f x =14.光线由点P （2，3）射到直线1-=+y x 上，反射后过点Q （1，1），则反射光线所在的 直线方程为15、将边长为a 的正方形ABCD 沿对角线AC 折起，使BD=a ，则三棱锥D —ABC 的体积为 16、在三棱锥S —ABC 中，SA ＝SB ＝SC ＝1，∠ASB ＝∠ASC ＝∠BSC ＝30°，一只蚂蚁从点A 出发沿三棱锥的表面爬行一周后又回到A 点，则蚂蚁爬过的最短路程为_____．三、解答题（共70分。