机车的两种启动方式

机车的两种启动方式通常讲机车的功率是指机车的牵引力的功率，P ＝F v 恒成立，与阻力f 无关，与P 是否为额定功率无关，与机车的运动状态无关。

机车可通过油门控制功率，可通过换档调整速度从而改变牵引力。

机车起动通常有两种方式，下面把这两种启动方式的规律总结如下：一、机车以恒定功率启动的运动过程 1、机车以恒定的功率P 启动后，若运动过程中所受的阻力不变，由于牵引力F ＝P ／v ，根据牛顿第二定律： F －f ＝ma 即 P ／v －f ＝ma所以： 当速度v 增大时，加速度a 减小。

当加速度a ＝0时，机车的速度达到最大，此时有： 。

以后，机车已v m 做匀速直线运动。

2、这一过程，F 、v 、a3、用v －t 图，这一过程可表示为右下图：最大速度之前是一段曲线。

4、以恒定功率启动的特点：（1）汽车在启动过程中先做加速度不断减小的加速运动，同时牵引力变小，当牵引力等于阻力时，开始以最大速度匀速运动。

（2）汽车在启动过程中的功率始终等于汽车的额定功率。

（3）汽车的牵引力和阻力始终满足牛顿第二定律F －f ＝ma 。

（4）汽车的牵引力和瞬时速度始终满足P －P 额＝F v 。

（5）在启动过程结束时，因为牵引力和阻力平衡，此时有 P 额＝F v m ＝f v m 。

（6）从能的角度看，启动过程中牵引力所做的功一方面用以克服阻力做功，另一方面增加汽车的动能。

二、机车以恒定加速度启动的运动过程1、机车以恒定的加速度a 启动时，牵引力F 、阻力f 均不变， 此时有：F －f ＝ma 。

机车匀加速运动的瞬时功率：P ＝Fv ＝（f ＋ma ）•v ＝（f ＋ma ）•a t ≤P 额。

匀加速阶段的最长时间t ＝P 额／［（ma ＋f ）a ］；匀加速运动的末速度为v t ＝P 额／（ma ＋f ）。

当机车达到这一速度时，其瞬时功率等于它的额定功率。

然后机车又做变加速运动。

此时加速度a 和第一种启动过程一样变化；这时的最大速度还是 。

机车起动的两种方式分析机车起动问题是指汽车、火车、轮船、摩托等动力机械的起动问题，而起动过程分为以恒定功率起动和恒力起动（先匀加速起动至额定功率后再变加速运动）两种情况，因起动过程中各物理量相互关联而又发生变化，过程比较复杂，有一定的难度．1．以恒定功率起动在此过程中，机车不断加速，因为开始时机车已经达到额定功率，根据P=Fv 可知在速度v 不断增大的时候，牵引力F 会不断减小，加速度F-f=ma （f 表示机车运动过程中受到的阻力）也不断减小，但因为加速度的方向和速度的方向相同，所以无论加速度a 怎样小，速度v 也是增加的．即机车一直做加速度减小的加速运动，直到F f =时，达到最大速度m P P v F f==，此后以v m 做匀速直线运动．起动过程结束的标志就是“速度不变”． 例1．汽车发动机的额定功率为60kw,汽车质量为5t,汽车在水平路面上行驶时，阻力是车中的0.1倍，g=10m/s 2问（1）汽车保持以额定功率从静止启动能达到的最大速度是多少？解析：由P =F·v 可知，汽车在额定功率下行驶，牵引力与速度成反比．速度增大，牵引力减小，当汽车的牵引力与所受阻力相等时，速度达到最大．所以v m =P /F f=60000/0.1×5000×10m/s = 12m/s ． 说明：此类问题主要把握住机车作加速度减小的加速运动，最终匀速的运动特点，利用F f =时，达到最大速度m P P v F f==来解题． 2．先以恒力起动至额定功率后再恒功率起动该起动过程分为两个阶段：阶段１是匀加速过程，在此过程中，速度v 由零开始不断增加，功率P 也由零开始逐渐增加；由F-f=ma ，因为加速度a 是不变的，所以在此过程中牵引力F 也是不变的．此过程的结束就是第二个过程的开始，以“功率P 达到最大即额定功率，但速度没有达到最大”为标志．阶段２中因为还有加速度的存在，所以速度v 会继续增加，在功率P 不变的情况下，根据P =Fv ，可知牵引力F 不断减小，加速度a 也相应减小．第二过程结束的标志就是“机车的功率P 最大，速度v 也是最大”，到此为止，整个起动过程结束．再以后，机车将以v m 做匀速直线运动，功率不变．例2．汽车发动机的额定功率为60 kW ，汽车的质量为4 t ，当它行驶在坡度为0.02的长直公路上时，如图１，所受阻力为车重的0.1倍(g ＝10 m/s 2)，求：⑴汽车所能达到的最大速度v m =？⑵若汽车从静止开始以0.6 m/s 2的加速度做匀加速直线运动，则此过程能维持多长时间？解析： ⑴汽车在坡路上行驶，所受阻力由两部分构成，即f ＝kmg ＋mg sin α=4000＋800N=4800 N ． 又因为F ＝f 时达到最大速度，且P =f·v m ，所以36010/12.5/sin 4800m P v m s m s kmg mg α⨯===+． ⑵汽车从静止开始，以a =0.6 m/s 2匀加速行驶，由F ＝ma ，有F ′－f －mg sin α＝ma ．故 3sin 7.210F kmg mg ma N α'=++=⨯ 保持这一牵引力，汽车匀加速行驶到速度mv '，此时达到额定功率，据P Fv =有图１8.33/m m P v m s F '=='． 由运动学规律可以求出匀加速行驶的时间8.3313.90.6m v t s s a '===． 说明：此后汽车将做加速度减小的加速运动，直到达到12.5m/s,而后匀速直线运动． ３．两种启动方式的共同点对同一机车，在相同条件下，两种启动方式最终都是F =f ，匀速时的速度v m 相同．v -t 图像如图２所示．例3．电动机通过一绳子吊起质量为8 kg 的物体，绳的拉力不能超过120 N ，电动机的功率不能超过1200 W ，要将此物体由静止起用最快的方式吊高90 m （已知此物体在被吊高接近90 m 时，已开始以最大速度匀速上升）试分析应如何吊起物体？达到最大功率的最短时间是多少？匀速时的速度是多少？解析： 此题可以采用机车起动类问题的思路，即将物体吊高分为两个过程处理：第一过程是以绳所能承受的最大拉力拉物体，使物体匀加速上升，第一个过程结束时，电动机刚达到最大功率．第二个过程是电动机一直以最大功率拉物体，拉力逐渐减小，当拉力等于重力时，物体开始匀速上升.在匀加速运动过程中加速度为a =8108120m ⨯-=-m mg F m/s 2=5 m/s 2 末速度v t =1201200=m m F P =10 m/s 上升的时间t 1=510=a v t s=2 s 此即达到最大功率的最短时间．在功率恒定的过程中，最后匀速运动的速率为v m =1081200⨯==mg F F P m m =15 m/s 说明：本题考查对机车启动两类问题的理解及迁移应用的创新能力．同学们往往对整个过程分析不透，若开始即以最大功率拉，绳会被拉断．v v 2。

机车的两种启动⽅式机车的两种启动⽅式机车启动通常有两种⽅式，即以恒定功率启动和以恒定加速度启动．1.机车以恒定功率启动的运动过程机车达到最⼤速度时，a＝0，F＝f，P＝Fv m＝fv m，这⼀启动过程的v－t图象如图所⽰．2.机车以恒定加速度启动的运动过程这⼀运动过程的v－t图象如图所⽰．(1)机车以恒定加速度启动时，先后经过两个过程，匀加速结束时的速度并未达到整个过程的最⼤速度v m，只是达到匀加速度阶段的最⼤速度．(2)在P＝Fv中，因为P为机车牵引⼒的功率，所以对应的F是牵引⼒并⾮合⼒．汽车的质量为2 000 kg，汽车发动机的额定功率为80 kW，它在平直的公路上⾏驶时所受的阻⼒是4 000 N，试求：(1)汽车保持额定功率从静⽌启动后达到的最⼤速度是多少？(2)若汽车以2 m/s2的加速度做匀加速直线运动，可维持多长时间？[思路点拨] 解答本题时应把握以下两点：(1)汽车匀速运动时的速度，是该功率下汽车所能达到的最⼤速度．(2)匀加速运动结束时P ＝P 额．[解析] 当汽车速度最⼤时，汽车做匀速直线运动．可根据受⼒平衡求出牵引⼒，再根据P ＝Fv 求出最⼤速度；在汽车的匀加速运动过程中，牵引⼒恒定，功率在变⼤，直到达到额定功率为⽌．(1)汽车以额定功率运⾏，其牵引⼒为F ＝P v汽车达到最⼤速度后做匀速直线运动，所以F ＝fv max ＝P F ＝P f ＝80×1034 000m/s ＝20 m/s. (2)汽车以恒定加速度启动后F ′－f ＝ma所以F ′＝f ＋ma ＝(4 000＋2 000×2) N ＝8 000 N.匀加速运动可达到的最⼤速度为v max ′＝P F ′＝80×1038 000 m/s ＝10 m/s. 所以匀加速运动的时间t ＝v max ′a ＝102s ＝5 s. [答案] (1)20 m/s (2)5 s解决汽车的启动问题，⾸先要明确属于恒定功率启动还是恒定加速度启动，其次要明确所求解的问题属于哪个阶段．若以恒定加速度启动，汽车先做匀加速运动，当功率达到额定功率后，汽车做变加速运动．2.质量为2 t 的汽车，发动机的牵引功率为30 kW ，在⽔平公路上，能达到的最⼤速度为15 m/s ，则当汽车的速度为10 m/s 时的加速度为( )A ．0.5 m/s 2B ．1 m/s 2C ．1.5 m/s 2D ．2 m/s 2解析：选A.当v ＝15 m/s 时，汽车所受牵引⼒F 与阻⼒f 相等，由P ＝Fv 得f ＝F ＝P v＝30×10315 N ＝2×103 N ；当v ′＝10 m/s 时，其牵引⼒为F ′＝P v ′＝30×10310 N ＝3×103 N ，由⽜顿第⼆定律得a ＝F ′－f m ＝3×103－2×1032×103m/s 2＝0.5 m/s 2.。

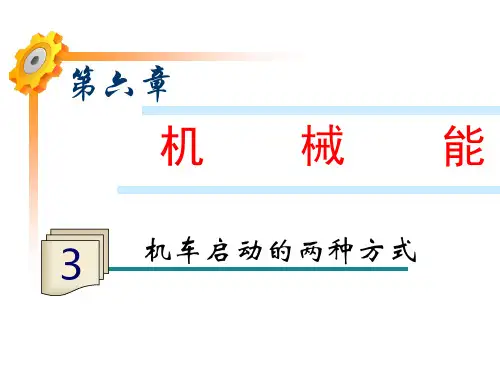
机车的两种启动方式通常讲机车的功率是指机车的牵引力的功率，P ＝F v 恒成立，与阻力f 无关，与P 是否为额定功率无关，与机车的运动状态无关。

机车可通过油门控制功率，可通过换档调整速度从而改变牵引力。

机车起动通常有两种方式，下面把这两种启动方式的规律总结如下：一、机车以恒定功率启动的运动过程 1、机车以恒定的功率P 启动后，若运动过程中所受的阻力不变，由于牵引力F ＝P ／v ，根据牛顿第二定律： F －f ＝ma 即 P ／v －f ＝ma所以：当速度v 增大时，加速度a 减小。

当加速度a ＝0时，机车的速度达到最大，此时有： 。

以后，机车已v m 做匀速直线运动。

2、这一过程，F 、v 、a3、用v －t 图，这一过程可表示为右下图：最大速度之前是一段曲线。

4、以恒定功率启动的特点：（1）汽车在启动过程中先做加速度不断减小的加速运动，同时牵引力变小，当牵引力等于阻力时，开始以最大速度匀速运动。

（2）汽车在启动过程中的功率始终等于汽车的额定功率。

（3）汽车的牵引力和阻力始终满足牛顿第二定律F －f ＝ma 。

（4）汽车的牵引力和瞬时速度始终满足P －P 额＝F v 。

（5）在启动过程结束时，因为牵引力和阻力平衡，此时有P 额＝F v m ＝f v m 。

（6）从能的角度看，启动过程中牵引力所做的功一方面用以克服阻力做功，另一方面增加汽车的动能。

二、机车以恒定加速度启动的运动过程1、机车以恒定的加速度a 启动时，牵引力F 、阻力f 均不变，此时有：F －f ＝ma 。

机车匀加速运动的瞬时功率：P ＝Fv ＝（f ＋ma ）•v ＝（f ＋ma ）•a t ≤P 额。

匀加速阶段的最长时间t ＝P 额／［（ma ＋f ）a］；匀加速运动的末速度为v t ＝P 额／（ma ＋f ）。

当机车达到这一速度时，其瞬时功率等于它的额定功率。

然后机车又做变加速运动。

此时加速度a 和第一种启动过程一样变化；这时的最大速度 还是。

专题1：机车的两种启动方式一、以恒定功率启动1．（2022春·陕西咸阳·高一期末）一辆汽车在水平公路上行驶，设汽车在行驶过程中所受阻力不变，汽车的发动机始终以额定功率输出。

关于牵引力和汽车速度，下列说法中正确的是（）A．汽车加速行驶时，牵引力不变，速度增大B．汽车加速行驶时，牵引力增大，速度增大C．汽车加速行驶时，牵引力减小，速度增大D．当牵引力等于零时，速度达到最大值【答案】C【详解】ABC．根据P Fv=由题意可知汽车的发动机始终以额定功率输出，可知汽车加速行驶时，汽车速度增大，牵引力减小，C正确，AB错误；D．当牵引力等于汽车所受阻力时，汽车速度达到最大值，D错误。

故选C。

2．（2022春·陕西渭南·高一渭南高级中学阶段练习）质量为m的汽车在平直公路上启动，阻力f保持不变，当它以加速度a加速到速度v时，发动机的实际功率正好等于额定功率P，从此时开始，发动机在额定功率下工作，则此后（）A．汽车的牵引力先减小后不变B．汽车的牵引力为f+maC．汽车的最大速度为PmaD．汽车的加速度在增大【答案】A【详解】ABD．由P Fv=，可知当达到速度v后，此时牵引力大于阻力，继续做加速运动，则牵引力减小，由牛顿第二定律可知F f ma-=汽车做加速度减小的加速运动，当牵引力等于阻力时，加速度减小到零，速度达到最大，所以汽车的牵引力先减小后不变，故A正确，BD错误；C．汽车的最大速度为故选A 。

3．（2022春·河北石家庄·高一阶段练习）（多选）连准扬镇高铁扬州段12月11日正式开通，如图所示，“复兴号”列车正沿直线驶出扬州东站，假设列车质量为m ，牵引电机的输出功率恒为P ，所受阻力恒为f 。

某时刻速度为1v 、加速度为1a ，一段时间t 后速度为2v ，在这段时间内位移为x 。

下列关系式正确的是（ ）A ．122v v x t +>B ．11P f a mv m =- C ．21112x v t a t =+ D ．22211122Pt mv mv =-可知速度增大，牵引力减小，加速度减小，即车做加速度减小的变加速直线运动，不是匀变速直线运动，则位移表达式不成立，C错误；A ．根据上述分析，作出v —t 图如图所示由于车做加速度减小的变加速直线运动，则该运动的位移大于如图虚线描述的匀加速直线运动的位移，则有B ．列车速度为v 1时，牵引力是1P v ，根据牛顿第二定律得解得B 正确；D ．根据动能定理可知解得D 错误。