下载文档原格式
3．5 贝叶斯网络贝叶斯网络是一系列变量的联合概率分布的图形表示。
一般包含两个部分，一个就是贝叶斯网络结构图，这是一个有向无环图（DAG），其中图中的每个节点代表相应的变量，节点之间的连接关系代表了贝叶斯网络的条件独立语义。
另一部分，就是节点和节点之间的条件概率表（CPT），也就是一系列的概率值。
如果一个贝叶斯网络提供了足够的条件概率值，足以计算任何给定的联合概率，我们就称，它是可计算的，即可推理的。
3.5.1 贝叶斯网络基础首先从一个具体的实例（医疗诊断的例子）来说明贝叶斯网络的构造。
假设：命题S(moker)：该患者是一个吸烟者命题C(oal Miner)：该患者是一个煤矿矿井工人命题L(ung Cancer)：他患了肺癌命题E(mphysema)：他患了肺气肿命题S对命题L和命题E有因果影响，而C对E也有因果影响。
命题之间的关系可以描绘成如右图所示的因果关系网。
因此，贝叶斯网有时也叫因果网，因为可以将连接结点的弧认为是表达了直接的因果关系。
图3-5 贝叶斯网络的实例tp3_5_swf.htm图中表达了贝叶斯网的两个要素：其一为贝叶斯网的结构，也就是各节点的继承关系，其二就是条件概率表CPT。
若一个贝叶斯网可计算，则这两个条件缺一不可。
贝叶斯网由一个有向无环图（DAG）及描述顶点之间的概率表组成。
其中每个顶点对应一个随机变量。
这个图表达了分布的一系列有条件独立属性：在给定了父亲节点的状态后，每个变量与它在图中的非继承节点在概率上是独立的。
该图抓住了概率分布的定性结构，并被开发来做高效推理和决策。
贝叶斯网络能表示任意概率分布的同时，它们为这些能用简单结构表示的分布提供了可计算优势。
假设对于顶点x i，其双亲节点集为P ai，每个变量x i的条件概率P(x i|P ai)。
则顶点集合X={x1,x2,…,x n}的联合概率分布可如下计算：双亲结点。
该结点得上一代结点。
该等式暗示了早先给定的图结构有条件独立语义。
3．1 概述一个人工智能系统，由于知识本身的不精确和不完全，采用标准逻辑意义下的推理方法难以达到解决问题的目的。
对于一个智能系统来说，知识库是其核心。
在这个知识库中，往往大量包含模糊性、随机性、不可靠性或不知道等不确定性因素的知识。
为了解决这种条件下的推理计算问题，不确定性推理方法应运而生。
归纳起来，不确定性推理方法研究产生的原因大致如下：·很多原因导致同一结果如多种原因引起同一种疾病。
例如，发烧可能因为感冒，也可能因为得了肺炎，需要进一步的知识才能作出具体判断。
·推理所需的信息不完备如勘探得到的地质分析资料不完备。
·背景知识不足由于人类认识水平的客观限制，客观世界的很多知识仍不为人们所认知。
在智能系统中，表现为所处理的知识的背景知识不完备。
如疾病的发病原因不十分明确。
·信息描述模糊这种现象十分普遍。
如"他不高不矮"，"今天不冷不热"等等。
在这类描述中，通常无法以一个量化的标准来描述，所描述的事物通常处在一个大致的范围。
比如，认为"身高在165cm－174cm 之间"的男士符合"不高不矮"的描述。
·信息中含有噪声噪声的存在干扰了人们对本源信息的认知，从而加大了认知上的难度。
如语音信号、雷达信号中的噪音干扰带来的信息模糊。
·规划是模糊的当需要对某个问题域进行划分时，可能无法找到一个清晰的标准。
如根据市场需求情况调节公司产品的内容和数量。
·推理能力不足必须考虑到实现的可能性，计算复杂度，系统性能。
如计算机的实现能力，推理算法的规模扩大能力有限等。
·解题方案不唯一没有最优方案，只有相对较优方案。
不实施，不能做出最后判断。
不精确思维并非专家的习惯或爱好所至，而是客观现实的要求。
在人类的知识和思维行为中，精确性只是相对的，不精确性才是绝对的。
知识工程需要各种适应不同类的不精确性特点的不精确性知识描述方法和推理方法。
3.2.1确定性方法以产生式作为知识表示的MYCIN 中，第一次使用了不确定性推理方法，给出了以确定性因子(Certainty Factor)或称可信度作为不确定性的度量。
1. 规则的不确定性度量规则以A →B 表示(认为A 为证据，B 为假设)，其中前提A 可以是一些命题的合取或析取。
MYCIN 系统引入可信度CF 作为规则不确定性度量。
CF 表示了增量P (B|A)－P(B)相对于P(B)或P(~B)的比值。
其中P 表概率。
（ P(B|A)表示事件A 已发生的条件下事件B 发生的概率） 规定 )()|( )()()|()()|( )()()|(),(B P A B P B P B P A B P B P A B P B P I B P A B P A B CF <-≥--⎩⎨⎧= CF(B,A)表示了证据A 为真时，相对于P(~B)=1-P(B)来说A 对B 为真的支持程度(当CF (B,A )≥0)。
或相对于P(B)来说A 对B 为真的不支持程度(当CF (B,A )<0)。
这种定义形式保证了－1≤CF(B,A)≤1当P(B|A)-P(B)相同时，P(B)小的CF小，P(B)大的CF大。
所以，CF(B,A)表达了证据A对假设B的影响程度。
CF(B,A)的几个特殊值:(1)前提A真，结论B必真的情形：由P(B|A)=1来体现，这时CF(B,A)=1。
(2)前提A与结论B无关的情形：由P(B|A)=P(B)来体现，这时CF(B,A)=0。
(3)前提A真,结论B必假的情形：由P(B|A)=0来体现，这时CF(B,A)= -1。
显然CF(B,A)≥0表示前提A真支持B真。
CF(B,A)<0表示前提A真不支持B真。
不难看出，CF(B,A)的定义借用了概率，但它本身并不是概率。
因为CF(B,A)可取负值，CF(B,A)+CF(B,~A)不必为1甚至可能为0。
实际应用中，A→B的CF(B,A)值是由专家主观确定的，并不是由P(B|A)来计算的。
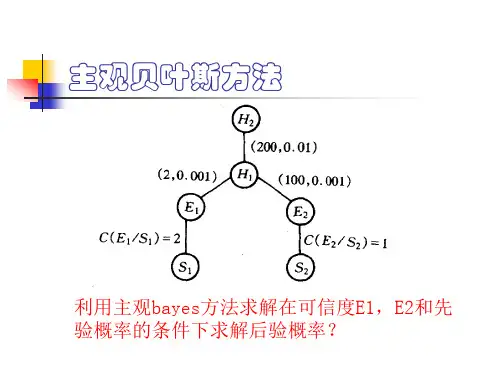
3.3主观Bayes 方法以语义网络表示的PROSPECTOR 系统，采用了主观Bayes 方法来度量不确定性。
引入两个数值(LS,LN) 作度量，LS 表示规则成立的充分性，LN 表示规则成立的必要性，这种表示既考虑了A 的出现对B 的支持，又考虑了A 的不出现对B 的影响。
3.3.1 对规则的不确定性度量直接使用Bayes 公式来做度量时，在计算P(B|A)时需要已知P(A|B)，为避开这个困难，提出了主观Bayes 方法。
对规则A →B 的不确定性f(B,A)以(LS,LN)来描述。
（1）LS 和LN 的定义)|~(~)|(~ )|~()|(B A P B A P LN B A P B A P LS ==（2）建立几率函数)(1)()(X P X P X O -=表示的是证据X 的出现概率与不出现概率之比，显然随P(X)的加大O （X ）也加大，而且有P(X)=0时 O(X)=0 （X 为假时）P(X)=1时 O(X)=∞ （X 为真时）这样，取值[0,1]的P(X)放大为取值[0,∞]便得O(X)。
（3）推导修改的Bayes 公式由于)()(~)|~()|(~)()()|()|(A P B P B A P A B P A P B P B A P A B P == 两者相比得)(~)()|~()|()|(~)|(B P B P B A P B A P A B P A B P ∙=这就是O (B|A)=LS ·O(B)相仿地也可得O(B|~A)=LN ·O(B)这两个公式就是修改的Bayes 公式。
称O(B)为结论的先验几率，称O (B|A)为结论的后验几率。
可以看出：● LS 表示A 真时，对B 为真的影响程度，表示规则A →B 成立充分性。
● LN 表A 假对B 为真的影响程度，表示规则A →B 成立的必要性。
（4）LS 和LN 的意义⎪⎩⎪⎨⎧<<>>== O(B),A)|O(B 1 O(B),)|B ( 1 O(B)A)|O(B ,1B A B A A O B A LS 不支持即当，支持即当，没有影响对，即当 ⎪⎩⎪⎨⎧<<>>==B A B A A B A LN 不支持即当，支持即当，没有影响对，即当~ O(B),A)|~O(B1~ O(B),)|~(O(B 1~O(B)A)|~O(B ,1 （5）LS 和LN 的关系由LS ，LN 的定义知，LS ，LN 均≥0，而且LS ，LN 不是独立取值的，只能出现以下3种情况：LS>1，LN<1LS<1，LN>1LS = LN = 1由于A 和~A 不会同时支持或排斥B ，所以不能出现两者同时>1或同时<1。
3．2 确定性方法以产生式作为知识表示方法的专家系统MYCIN中，第一次使用了不确定性推理方法，给出了以确定性因子或称可信度作为不确定性的度量。
这种推理方法必须解决几个方面的核心问题，即规则和证据的不确定性度量问题，不确定性的传播与更新问题。
MYCIN系统研制过程中产生了不确定推理方法，该方法是第一个采用了不确定推理逻辑的专家系统，在20世纪70年代非常有名。
这个系统提出该确定性方法时遵循了下面的原则：（1）不采用严格的统计理论。
使用的是一种接近统计理论的近似方法。
（2）用专家的经验估计代替统计数据（3）尽量减少需要专家提供的经验数据，尽量使少量数据包含多种信息。
（4）新方法应适用于证据为增量式地增加的情况。
（5）专家数据的轻微扰动不影响最终的推理结论。
注意：这种方法在理论上实质是以定量法为工具，比较法为原则的相对确认理论。
因此，采用此方法的MYCIN系统的诊断结果不是只给出一个最可信结论及其可信度，而是给出可信度较高的前几位，供人们比较选用。
3.2.1 规则的不确定性度量在逻辑推理过程中，常常以A → B表示规则。
其中A表示前提，可以是一些命题的析取或合取；B表示结论或推论，是在前提A下的直接逻辑结果。
在精确逻辑推理中，通常只有真假的描述：若A真，则B也必为真。
但在不确定推理过程中，通常要考虑的是A为真时对B为真的支持程度，甚至还考虑A为假（不发生）时对B为真的支持程度。
为此，引入规则的不确定性度量。
有规则A → B，其可信度CF(B, A)定义如下：CF(B,A)表示的意义：证据为真是相对于P(～B) = 1 - P(B)来说，A对B为真的支持程度，即A发生更支持B发生，此时CF(B,A)≥ 0。
相对于P(B)来说，A对B为真的不支持程度。
即A发生不支持B发生，此时CF(B,A)< 0。
它总是满足条件-1 ≤ CF(B,A) ≤ 1。
CF(B, A)的特殊值：CF(B, A) = 1，前提真，结论必真CF(B, A) = -1，前提真，结论必假CF(B, A) = 0 ，前提真假与结论无关实际应用中CF(B, A)的值由专家确定，并不是由P(B|A), P(B)计算得到的。
3.3主观Bayes方法
R.O.Duda等人于1976年提出了一种不确定性推理模型。
在这个模型中，他们称推理方法为主观Bayes方法，并成功的将这种方法应用于地矿勘探系统PROSPECTOR中。
在这种方法中，引入了两个数值（LS，LN），前者体现规则成立的充分性，后者则表现了规则成立的必要性，这种表示既考虑了事件A的出现对其结果B的支持，又考虑了A的不出现对B的影响。
在上一节的CF方法中，CF（A）<0.2就认为规则不可使用，实际上是忽视了A不出现的影响，而主观Bayes方法则考虑了A 不出现的影响。
t3-B方法_swf.htm
Bayes定理：
设事件A1，A2，A3，…，An中任意两个事件都不相容，则对任何事件B有下式成立：
该定理就叫Bayes定理，上式称为Bayes公式。
全概率公式：
可写成：
这是Bayes定理的另一种形式。
Bayes定理给出了一种用先验概率P（B|A），求后验概率P （A|B）的方法。
例如用B代表发烧，A代表感冒，显然，求发烧的人中有多少人是感冒了的概率P（A|B）要比求因感冒而发烧的概率P（B|A）困难得多。
3.3.1规则的不确定性
为了描述规则的不确定性，引入不确定性描述因子LS,LN：对规则A→B的不确定性度量f（B，A）以因子（LS，LN）来描述：
表示A真时对B的影响，即规则成立的充分性
表示A假时对B的影响，即规则成立的必要性
实际应用中概率值不可能求出，所以采用的都是专家给定的LS,LN值。
从LS，LN的数学公式不难看出，LS表征的是A的发生对B发生的影响程度，而LN表征的是A的不发生对B发生的影响程度。
几率函数O(X)：
即，表示证据X的出现概率和不出现的概率之比，显然O(X)是P(X)的增函数，且有：
P(X)＝0，O(X)＝0
P(X)＝0.5，O(X)＝1
P(X)＝1，O(X)＝∞，几率函数实际上表示了证据X的不确定性。
几率函数与LS,LN的关系：
O(B|A)=LS·O(B)
O(B|~A)=LN·O(B)
几个特殊值：
LS、LN≥0，不独立。
LS,LN不能同时＞1或＜1
LS,LN可同时＝1
3.3.2证据的不确定性
证据的不确定性度量用几率函数来描述：
虽然几率函数与概率函数有着不同的形式，但是变化趋势是相同的：当A为真的程度越大（P(A)越大）时，几率函数的值也越大。
由于几率函数是用概率函数定义的，所以，在推理过程中经
常需要通过几率函数值计算概率函数值时，此时可用如下等式：
3.3.3推理计算
由于是不确定性推理，所以必须讨论证据发生的各种可能性。
①A必出现时（即P(A)＝1）:
O(B|A)=LS·O(B)
O(B|~A)=LN·O(B)
②当A不确定时即P(A)≠1时
设A'代表与A有关的所有观察，
P(B|A')=P(B|A)P(A|A')+P(B|～A)P(～A|A')
当P(A|A')=1时，证据A必然出现
当P(A|A')=0时，证据A必然不出现
当P(A|A')=P(A)时，观察A'对A没有影响：
P(B|A')=P(B)
这样可得P(A|A')为0，P(A)，1时相应的P(B|A')的值，根据这三点可以得到线性插值图，见图3-2。
P(A|A')的其它取值下的P(B|A')可根据此图通过线性插值法得到。
更简单的还有用两点直线插值的，当然也可以用更复杂的插
值方法，只要你有足够的数据。
图3-2线性插值图
t3-2插值_swf.htm
当证据不确定时，证据理论推理的基本原理是，从该证据A 往前看，即寻找A的出处。
如果A是由A'导出的，即A'→A→B,则当A不清楚的时候，采用A'的相关信息进行计算。
如果还不行，就再往前推。
是一个递归推导的过程。
注意：A'是指从A向前看的各个相关证据，所以有时可能存在多个相关证据。
③当存在两个证据时
P(A1∧A2|A')=min{P(A1|A'),P(A2|A')}
P(A1∨A2|A')=max{P(A1|A'),P(A2|A')}
④多个观察时
若A1→B，A2→B而A1，A2相互独立，对A1，A2的观察分别为A1',A2'
例题1
已知：P(A)=1,P(B1)=0.04,P(B2)=0.02
R1:A→B1LS=20LN=1
R2:B1→B2LS=300LN=0.001
计算：P(B2|A)
分析：当使用规则R2时，证据B1并不是确定的发生了，即P(B1)≠1，因此要采用插值方法。
解：
先依照A必然发生，由定义和R1得：
O(B1)=0.04/(1-0.04)=0.0417
O(B1|A)=LS*O(B1)=0.83
P(B1|A)=0.83/(1+0.83)=0.454
然后假设P(B1|A)=1,计算：
P(B2|B1)=300*0.02/(300*0.02+1)=0.857
最后进行插值：
P(B2|A)=0.02+(0.857-0.02)*(0.454-0.04)/(1-0.04)
=0.410
例题2
已知：证据A1，A2必然发生，且P（B1）＝0.03，P（B2）＝0.01，规则如下：
R1：A1→B1LS=20LN=1
R2：A2→B1LS=300LN=1
R3：B1→B2LS=300LN=0.0001
求B1，B2的更新值。
解：
先求B1的更新值：
依R1，P1（B）＝0.03
O（B1）＝0.03/(1-0.03)=0.030927
O(B1|A1)=LS×O(B1)=20×0.030927=0.61855
P(B1|A1)=0.61855/(1+0.61855)=0.382
使用规则R1后，B1的概率从0.03上升到0.382
依R2：
O(B1|A1A2)=300×O(B1|A1)=185.565
P(B1|A1A2)=185.565/(1+185.565)=0.99464
使用规则R2后，B1的概率从0.382上升到0.99464
再求B2的更新值：
由于B1不确定所以讨论其前项证据A，
证据A必然发生时，由以上计算可知P（B1）＝0.03，规则R1：A1→B1LS=20LN=1
对于规则R1，证据A必然发生，可得
P（B1|A）＝0.382；
但是使用规则R3时，B1并非确定地发生，因此要用插值法。
先假设P（B1|A）＝1，此时
P（B2|B1）＝300*0.01/((300-1)*0.01+1)(公式（1）)
＝0.75188
再假设P（B1|A）＝P(B1)=0.03时，即A对B1无影响
P（B2）＝0.01
根据这两个值可进行插值计算：
P（B2|A）=0.01+(0.75188-0.01)*(0.382-0.03)/(1-0.03)
=0.305105
总结
主观Bayes方法优点：直观，明了。
问题：要求B j个事件相互独立（无关），实际上是不可能的。
P(A/B i)和P(B i)难以计算。
实际应用中，为了避开这一点采用LS,LN的专家给定值。
