常用逻辑电路
- 格式:doc
- 大小:190.50 KB
- 文档页数:8


以下是八种逻辑门电路的真值表:1. 与门(AND):所有输入为高时,才会有输出高。
真值表如下:* 输入A
* 输入B
* 输出Y
* 0
* 0
* 0
* 0
* 1
* 0
* 0
* 1
* 1
* 1
2. 或门(OR):所有输入为低时,才会有输出低。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
* 0
* 0
* 1
* 1
* 1
* 0
3. 非门(NOT):逆转输入的高低状态。
真值表如下:
* 输入A
* 输出Y
* 0
* 1
4. 与非门(NAND):所有输入为高时,才会有输出低。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
* 1
* 0
* 1
* 1
5. 或非门(NOR):所有输入为低时,才会有输出高。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
* 0
6. 异或门(XOR):输入相同时输出为低,否则为高。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
7. 同或门(XNOR):与异或门相反。
输入相同时输出为高,否则为低。
真值表如下:
8. 与门的逻辑符号为AND,或门的逻辑符号为OR,非门的逻辑符号为NOT,与非门的逻辑符号为NAND,或非门的逻辑符号为NOR,异或门的逻辑符号为XOR,同或门的逻辑符号为XNOR。

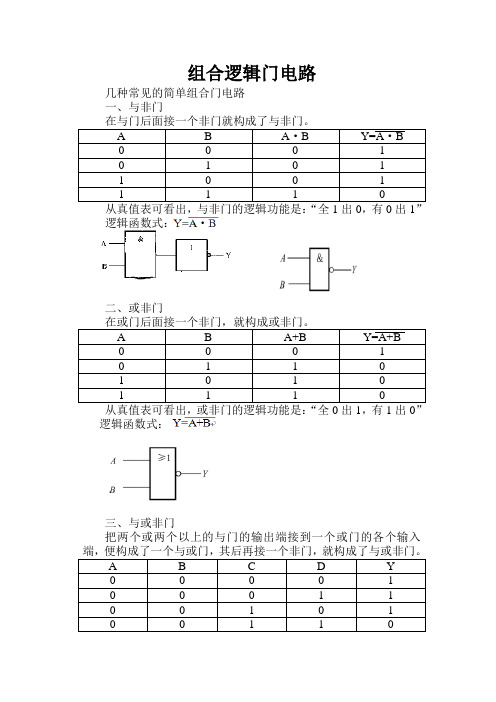
组合逻辑门电路几种常见的简单组合门电路一、与非门在与门后面接一个非门就构成了与非门。
A B A·B Y=A·B0 0 0 10 1 0 11 0 0 11 1 1 0从真值表可看出,与非门的逻辑功能是:“全1出0,有0出1”逻辑函数式:二、或非门在或门后面接一个非门,就构成或非门。
A B A+B Y=A+B0 0 0 10 1 1 01 0 1 01 1 1 0从真值表可看出,或非门的逻辑功能是:“全0出1,有1出0”逻辑函数式:三、与或非门把两个或两个以上的与门的输出端接到一个或门的各个输入端,便构成了一个与或门,其后再接一个非门,就构成了与或非门。
A B C D Y0 0 0 0 10 0 0 1 10 0 1 0 10 0 1 1 00 1 0 0 10 1 0 1 10 1 1 0 10 1 1 1 01 0 0 0 11 0 0 1 11 0 1 0 11 0 1 1 01 1 0 0 11 1 0 1 11 1 1 0 11 1 1 1 0从真值表、逻辑函数可看出,与或非门的逻辑功能是:当输入端中任何一组全为1时,输出即为0,;只有各组输入都至少有一个为0时,输出才能为1.逻辑函数式:Y=AB+CD四、异或门A B Y0 0 00 1 11 0 11 1 0逻辑函数式:Y= 或或Y=A○+B从逻辑函数式及真值表可看出,异或门的逻辑功能是:当两个输入端的状态相同(都为0或都为1)时输出为0;反之,当两个输入端状态不同(一个为0,另一个为1)时,输出端为1。
五、同或门A B Y0 0 10 1 01 0 01 1 1逻辑函数式:Y=或Y=A○·B从逻辑函数式及真值表可看出同或门的逻辑功能是:当两个输入端的状态相同(都为0或都为1)时输出为1;反之,当两个输入端状态不同(一个为0,另一个为1)时,输出端为0。

数字逻辑电路中共8种:有与门,或门,非门,与非门,或非门,同或门,异或门,与或非门它们在逻辑电路中分别起什么作用?
与门:逻辑乘(好像数学中的交集)有0出0,全1出1。
Y=AB。
或门:逻辑加(好像并集)有1出1,全0出0。
Y=A+B。
非门:“非”即否定,也称反相器。
0出1,1出0。
Y=非A。
或非门:全0出1,有1出0。
F=非(A+B)。
异或门:输入相同为0,相异为1,(全0或全1才出0)。
F=A⊕B=(非A)·B+A·(非B)。
作用是判断输入端是否一致!
同或门:全0或全1才出1。
F=A⊙B=A·B+(非A)·(非B)。
作用也是判断输入端是否一致!
与非门:全1出0,有0出1。
F=非(AB)。
先进行与运算,然后是非运算。
如输入A=1,B=0,输出Y=/AB=1。
AB的与运算结果为0,然后输出为非运算后,结果就为1. 同理输入A=1,B=1,输出 Y=/AB=0。
与或非门:。
序在现代电子学和计算机科学中,逻辑门电路是至关重要的基础组成部分。
而逻辑门电路最基本的形式就是7种逻辑门,它们分别是与门、或门、非门、异或门、与非门、或非门以及同或门。
每种逻辑门都有其独特的逻辑符号和逻辑表达式,它们在数字电子电路中扮演着不可或缺的角色。
接下来,我们将深入探讨这7种逻辑门电路的逻辑符号和逻辑表达式,并从浅到深逐步分析它们的原理和应用。
一、与门与门是最简单的逻辑门之一,它的逻辑符号是一个“Λ”形状,而其逻辑表达式可以用“Y=A·B”来表示。
在与门电路中,只有当输入的布尔值均为1时,输出才会为1;否则输出为0。
这个逻辑表达式实际上就表明了与门的原理,即只有当所有输入为真时,输出才为真。
二、或门或门的逻辑符号是一个“V”形状,而其逻辑表达式可以用“Y=A+B”来表示。
与与门相反,或门只要有一个输入为1,输出就为1;只有当所有输入为0时,输出才为0。
可以看出,或门的逻辑表达式和与门的逻辑表达式是相对应的。
三、非门非门的逻辑符号是一个“¬”形状,而其逻辑表达式可以用“Y=¬A”来表示。
非门的原理是将输入的布尔值取反,即如果输入为1,则输出为0;如果输入为0,则输出为1。
四、异或门异或门的逻辑符号是一个带有一个加号的“⊕”形状,而其逻辑表达式可以用“Y=A⊕B”来表示。
异或门的原理是只有当输入不同时为1时,输出为1;否则输出为0。
异或门也常被用于比较两个输入是否相等的情况。
五、与非门与非门实际上是与门和非门的组合,其逻辑符号是一个与门后加上一个小圆点的符号,而其逻辑表达式可以用“Y=¬(A·B)”表示。
与非门的原理是先进行与运算,再对结果取反。
六、或非门或非门实际上是或门和非门的组合,其逻辑符号是一个或门后加上一个小圆点的符号,而其逻辑表达式可以用“Y=¬(A+B)”表示。
或非门的原理是先进行或运算,再对结果取反。
七、同或门同或门的逻辑符号是一个带有一个加号和一个横线的“⊙”形状,而其逻辑表达式可以用“Y=¬(A⊕B)”表示。
常用逻辑电路
在逻辑电路中,输入和输出只有两种状态,即高电平和低电平。
通常以逻辑“1”和“0”表示电平高低。
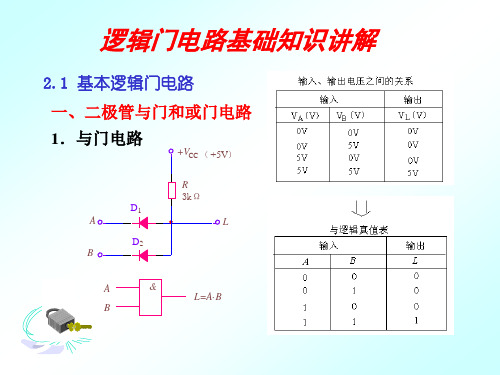
1、与门
是一个能够实现逻辑乘运算的、多端输入、单端输出的逻辑电路。
逻辑解释:
即如右边图所示,当开关A与B当中只有全部闭合(即为高电平1)时,才会有输出(即灯泡才会亮)所以在与门电路中,只有输入的全部条件为高电平“1”时输会有输出。
2、或门
是一个能够实现逻辑加运算的、多端输入、单端输出的逻辑电路。
逻辑解释:
即如右边图所示,当开关A与B当中只要有一个开关闭合(即为高电平1)时,就会有输出(即灯泡才会亮)所以在或门电路中,只要输入的为高电平“1”就会有输出。
语言表达为:“有1出1,全0出0”。
3、非门
是一个能够实现逻辑非运算的、单端输入、单端输出的逻辑电路。
非就是反,就是否定,也就是输入与输出的状态总是相反。
逻辑解释:
如右边图所示,当开关K断开时灯亮,开关闭合时灯灭。
如以开关断开为灯亮,开关接通为灭为结果,则开关K与灯泡的因果关系为非逻辑关系。
语言表达为:“有0出1,有1出0”。
复合逻辑门电路:
4.与非门
将一个与门与一个非门联接起来就构成了一个与非门。
根据与门和非门的逻辑功能,可以列出与非门逻辑关系真值表。
其逻辑功能的特点是:“当输入全为1,输出为0;只要输入有0,输出就为1”。
5.或非门
将一个或门与一个非门联接起来就构成了一个或非门。
根据或门和非门的逻辑功能,可以列出与非门逻辑关系真值表。
其逻辑功能的特点是:
“当输入全为0,输出为1;只要输入有1,输出就为0”。
6.异或门
异或门只有两个输入端和一个输出端,。
其逻辑功能的特点是:“当两个输入端一个为0,另一个为1时输出为1,当两个输入端均为1或均为0时,输出为0”。
真值表如下:
异或门的作用是:把两路信号进行比较,判断是否相同。
当两路输入信号不同,即一个为高电平,一个为低电平时,输出为高电平。
反之当两个输出端信号相同时,即为高电平或低电平时,输出为低电平”。
触发器:
触发器是计算机记忆装置的基本单元,它具有把以前的输入‘记忆’下来的功能,一个触发器能储存一位二进制代码。
下面我们简单的来介绍计算机中常用的几中触发器。
1.R-S 触发器
R-S 触发器的逻辑符号如下图所示,它有两个输入端,两个输出端。
其中,S 为置位信号输入端,R 为复位信号输入端;Q
和Q 非为输出端。
规定Q 为高、Q 非为低时,该触发器为1状态;反之为0状态。
其真值表如下。
2.D 触发器
D 触发器又称数据触发器,它的逻辑符号如下图所示,R 、S 分别为强制置0、置1端,触发器的状态是由时钟脉冲CLK 上升沿到来时D 端的状态决字。
当D=1时,触发器为1状态;反之为0状态。
其真值表如下
3.J-K触发器
J-K触发器的逻辑符号如下,R、S分别为强制置0、置1端。
K为同步置0输入端,J 街?输入端。
触发器的状态是由时钟脉冲CLK下降沿到来时J、K端的状态决定,其真值表如下
J-K触发器的逻辑功能比较全面,因此在各种寄存器、计算器、逻辑控制等方面应用最为广泛。
但在某些情况,如二进制计数、移位元、累加等,多用D 触发器。
由于D触发器线路简章,所以大量应用于移位寄存器等方面。
寄存器:
寄存器是由触发器组成的,一个触发器是一个一位寄存器。
多个触发器就可以组成一个多位的寄存器。
由于寄存器在计算机中的作用不同,从而被命名不同,常用的有缓冲寄存器、移位寄存器、计数器等。
下面我们就简单的来介绍下这些寄存器的电路结构及工作原理。
1.缓冲寄存器
它是用来暂存某个数据,以便在适当的时间节拍和给定的计算步骤将数据输入或输出到其它记忆单元中去,下图是一个并行输入、并行输出的4位缓冲器的电路原理图,它由4个D触发器组成。
启动时,先在清零端加清零脉冲,把各触发器置0,即Q端为0。
然后,把数据加到触发器的D输入端,在CLK时钟信号作用下,输入端的信息就保存在各触发器中(D0~D3)。
2.移位寄存器
移位寄存器能将所储存的数据逐位向左或向右移动,以达到计算机运行过程中所需的功能,请看下图
启动时,先在清零端加清零脉冲,使触发器输出置0。
然后,第一个数据D0加到触发器1的串行输入端,在第一个CLK脉冲的上升沿Q0=Q0,Q1=Q2。
Q3=Q0。
其后,第二个数据D1加到串行输入端,在第二个CLK脉冲到达时,Q0=Q1,Q1=Q0,Q2=Q3=0。
以此类推,当第四个CLK来到之后,各输出端分别是Q0=Q3,Q1=Q2,Q2=Q1,Q3=Q0。
输出数据可用串行的形式取出,也可用并行开式取出。
3.计数器
计数器也是由若干个触发器组成的寄存器,它的特点是能够把存款在其中的数据加1或减1。
计数器的种类也很多,有行波计数器、同步计数器等,下面我们就以行波计数器向大家作个介绍。
下图就是一个由J-K触发器组成的行波计数器的工作原理图。
这种计数器的特点是:第一个时钟脉冲促使其最低有效位加1,使其由0变1;第二个时钟脉冲促使最低有效位由1变0。
同时推动第二位,使其由0变1;同理,第二位由1变0时又去推动第三位,使其由0变1,这样有如水波前进一样逐位进位下去。
上图中各位的J、K输入端都是悬浮的,这相当于J、K输入端都是置1淖刺锤魑欢即τ谧急阜淖刺V灰敝勇龀灞哐匾坏剑钣冶叩拇シ⑵骶突岱碤由0
转为1或由1转为0。
上图中的这个计数器是4位的,因此可以计0~15的数。
如果要计更多的数,需要增加位数,如8位计数器可计0~255的数,16位则可计0~65535的数。
4.三态门(三态缓冲器)
为减少信息传输线的数目,大多数计算机中的信息传输线均采用总线形式,即凡要传输的同类信息都走同一组传输线,且信息是分时传送的。
在计算机中一般有三组总线,即数据总线、地址总线和控制总线。
为防止信息相互干扰,要求凡挂在总线上的寄存器或内存等,它的传输端不仅能呈现0、1两个信息状态,而且还应能呈现第三种状态——高阻抗状态(又称高阻状态),即此时好像它们的输出被断开,对总线状态不起作用,此时总线可由其它器件占用。
三态门即可实现上述的功能,它除具有输入输出端之外,还有一控制端,请看下图。
当控制端E=1时,输出=输入,此时总线由该器件驱动,总线上的数据由输入数据决定;
当控制端E=0时,输出端呈高阻抗状态,该器件对总线不起作用。
当寄存器输出端接至三态门,再由三态门输出端与总线连接起来,就构成三态输出的级冲寄存器。
如下图所示就是一个4位的三态输出缓冲寄存器。
由于这里采用的是单向三态门,所以数据只能从寄存器输出到数据总线。
如果要实现双向传送,则要用双向三态门。
在这里有个问题问下大家,前面我们已把触发器,寄存器的概念跟大家讲解了一下,那么触发器、寄存器、内存,这三者之间是一个什么样的关系呢?答:通过前面的学习,我们知道触发器是计算机记忆装置的基本单元,一个触发器能储存一位二进制代码。
寄存器是由触发器组成的。
一个触发器就职一个一位的寄存器,多个触发器就可以组成一个多位的寄存器。
内存是由大量寄存器组成的,其中每一个寄存器就称为一个存储单元。
它可以存放一个有独立意义的二进
制代码。