6 均匀设计

•均匀设计方法•一、均匀试验设计•均匀设计是在正交试验设计的基础上，创造出的一种新适用于多因素、多水平试验的试验设计方法。

•均匀设计特别适合需要考察因素因素变化范围较大，且每个因素有较多水平的试验设计问题。

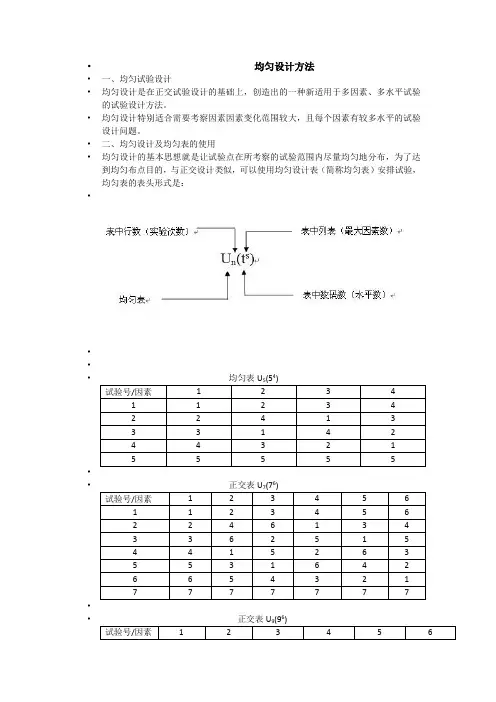
•二、均匀设计及均匀表的使用•均匀设计的基本思想就是让试验点在所考察的试验范围内尽量均匀地分布，为了达到均匀布点目的，与正交设计类似，可以使用均匀设计表（简称均匀表）安排试验，均匀表的表头形式是：••••4••正交表U6••正交表U6•••三、均匀表的特点• 1.任何一列，各水平仅出现一次；• 2.任何两列同行数码构成的有序数对仅出现一次；• 3.均匀表中任两列组成的试验方案不等价; 因此，每个均匀表都附加了使用表，告诉我们如何挑选相应的列按排试验。

• 4.当因素的水平数增加时，试验次数按水平数增加；• 5.使用表最多可安排的因素数都比均匀表列数少。

只能安排（s/2+1）个因素•四、用均匀表安排试验的步骤• 1.根据试验的目的，确定考察的指标；• 2.选择合适的因素和因素的考察范围；• 3.选择合适该项试验的均匀表，然后根据该表的使用表从中选出列号，将因素分别安排到相应的列号上；• 4.确定各因素的水平，并将这些因素的水平按所在列的指示分别对号号入座。

最后进行试验。

• 5.对实验结果进行分析，确定最佳的试验方案。

•例1．在阿魏酸的合成工艺考察中，选取原料配比，吡啶量，反应时间三个因素进行考察，试验的考察指标是阿魏酸的收率。

因素的变化范围如下：•原料配比A：1.0~3.4•吡啶量B：10~28(ml)•反应时间C：0.5~3.5(hr)•试用均匀设计安排试验。

•解:对于三个因素，s/2+1=3，求出s=4或5，考虑试验的承受程度，选用U7（76）均匀表安排试验，根据各因素的变化范围，划分因素水平表如下：••由U7（76）均匀表的配套使用表可知，应选1，2，3列，因而得下面的试验设计表:••将各因素所对应的水平值填入表中，得试验表如下，按试验表中每个试验的条件安排试验，将所得结果填入表最右列。

均匀设计的基本步骤
均匀设计是一种实验设计方法，用于在有限次试验中寻找最佳的试验条件。

以下是均匀设计的基本步骤：
1.确定实验目的和响应变量：首先需要明确实验的目的，确定要研究的响应变量，以便于确定实验的主要内容和目标。

2.确定实验因素和水平：根据专业知识和实际经验，选择对响应变量影响较大的因素作为实验因素。

根据实际情况和历史数据，为每个实验因素选择适当的水平。

3.制定均匀设计表：根据实验因素和水平的数量，选择合适的均匀设计表进行实验。

均匀设计表是一种特殊的矩阵，用于安排实验并确保各因素水平在实验中均匀分布。

4.安排实验：根据均匀设计表，安排实验的具体实施方案。

确保每个实验条件只被试验一次或多次，以确保结果的准确性。

5.收集数据：按照实验方案进行实验，并记录各实验条件下的响应变量值。

6.分析数据：对收集到的数据进行分析，探索各因素与响应变量之间的关系。

可以采用回归分析、方差分析等方法进行数据分析。

7.优化条件：根据数据分析结果，选择最优的实验条件进行进一步优化。

这可能涉及对实验方案进行调整或重复试验。

8.验证和确认：对优化后的条件进行验证和确认，以证明其在实践中具有可行性和有效性。

9.总结和报告：整理实验过程和结果，编写详细的实验报告，总
结实验的经验和教训，并提出改进意见和建议。

以上步骤是一个典型的均匀设计过程的基本流程。

具体的实施过程中，可以根据实际需求和条件进行调整和优化。

单因素6水平均匀设计
单因素6水平均匀设计是一种实验设计方法，用于研究一个因素对结果变量的影响。

在该设计中，将一个因素分为6个水平，每个水平都有相同数量的观测值。

以下是单因素6水平均匀设计的步骤：
确定因素和水平：首先确定要研究的因素，并将其分为6个水平。

确保每个水平的差异程度相对均匀，并且能够涵盖因素的全部范围。

确定观测值数量：确定每个水平的观测值数量，这些观测值数量应该相等。

通常情况下，观测值的数量越多，实验结果的可靠性越高。

随机化实验次序：为了消除实验中其他可能的干扰因素，需要随机化实验次序。

这样可以减小实验结果的偏差，并增加实验结果的可靠性。

进行实验并记录数据：按照随机化的实验次序，进行实验并记录结果变量的数据。

确保在每个水平上的观测值都得到准确记录。

数据分析：
对实验结果进行数据分析，可以使用统计方法，如方差分析。

通过分析结果，可以确定因素对结果变量的影响是否显著。

结果解释和推论：
根据数据分析的结果，解释因素对结果变量的影响，并进行推论。

根据推论，可以对因素的不同水平进行比较，并得出结论。

单因素6水平均匀设计的优点是简单易行，容易分析和解释结果。

然而，它也
有一些限制，如无法分析因素与其他因素的交互作用。

因此，在实际应用中，需要根据具体的研究目的和需求来选择合适的实验设计方法。

均匀试验设计均匀设计均匀设计(uniform design)是中国数学家方开泰和王元于1978年首先提出来的，它是一种只考虑试验点在试验范围内均匀散布的一种试验设计方法。

与正交试验设计类似、均匀设计也是通过一套精心设计的均匀表来安排试验的。

由于均匀设计只考虑试验点的“均匀散布”，而不考虑“整齐可比”，因而可以大大减少试验次数，这是它与正交设计的最大不同之处。

例如，在因素数为5，各因素水平数为31的试验中，若采用正交设计来安排试验，则至少要作312 =961次试验，这将令人望而生畏，难以实施，但是若采用均匀设计，则只需作31次试验。

可见，均匀设计在试验因素变化范围较大，需要取较多水平时，可以极大地减少试验次数。

经过20多年的发展和推广，均匀设计法已广泛应用于化工、医药、生物、食品、军事工程、电子、社会经济等诸多领域，并取得了显著的经济和社会效益。

1. 均匀设计表1.1 等水平均匀设计表均匀设计表，简称均匀表，是均匀设计的基础，与正交表类似，每一个均匀设计表都有一个代号，等水平均匀设计表可用U n ( r l)或U n* (r l)表示，其中，U为均匀表代号；n为均匀表横行数(需要做的试验次数)；r为因素水平数，与n相等；l为均匀表纵列数。

代号U右上角加“*”和不加“*”代表两种不同的均匀设计表，通常加“*”的均匀设计表有更好的均匀性，应优先选用。

表1-1、表1-3分别为均匀表U7 (74)与U7* (74)，可以看出，U7 ( 74)和U7*(74)都有7行4列，每个因素都有7个水平，但在选用时应首选U7*(74 )。

表1-1 U7 (74)表1-2 U7 (74)的使用表表1-3 U7* (74)表1-4 U7* (74)的使用表每个均匀设计表都附有一个使用表，根据使用表可将因素安排在适当的列中。

例如，表1-2是U7 ( 74)的使用表，由该表可知，两个因素时，应选用1，3两列来安排试验；当有三个因素时，应选用1,2,3三列，……。

均匀设计方法简介在工农业生产和科学研究中，常须做试验，以获得予期目的：改进生产工艺，提高产品收率或质量，合成出某化合物等等。

怎样做试验，是大有学问的。

本世纪30年代，费歇（R.A.Fisher）在试验设计和统计分析方面做了一系列先驱工作，使试验设计成为统计科学的一个分支。

今天，试验设计理论更完善，试验设计应用更广泛。

本节着重介绍均匀设计方法。

一、试验设计对于一项试验，例如用微波加热法通过离子交换制备Cu13X分子筛。

我们可以13X分子筛、CuCl2为原料来制备，为寻找最佳条件，应如何设计这个试验呢？若我们已确定了微波加热功率（A）、交换时间（B）、交换液摩尔浓度（C）为三个影响因素，每个因素取五个不同值（即水平：A1，…，A5，B1，…，B5，C1，…，C5）。

有两种方法最易想到：1．全面试验：将每个因素的不同水平组合做同样数目的试验。

对上述示例，不计重复试验，共需做5×5×5=125次试验。

2．多次单因素试验：依次考查各因素（考查某因素时，其它因素固定）取最佳值。

容易知道，对上示例（不计重复试验）共需做3×5=15次试验。

该法在工程和科学试验中常被人们采用，可当考查的因素间有交互作用时，该法所得结论一般不真。

3．正交设计法：利用正交表来安排试验。

本世纪60年代，日本统计学家田口玄一将试验设计中应用最广的正交设计表格化，使正交试验设计得到更广泛的使用。

70年代以来，我国许多统计学家深入工厂、科研单位，与广大工程技术人员、工人一起，广泛开展正交设计的研究、应用，取得了大批成果。

该法是目前最流行，效果相当好的方法。

正交表记为：L n(q m)，这里“L”表示正交表，“n”表总共要做的试验次数，“q”表每个因素都有q个水平，“m”表该表有4列，最多可安排m个因素。

常用的二水平正交表为L4(23)，L8(27)，L16(215)，L32(231)；三水平正交表有L9(34)，L27(313)；四水平正交表L16(45)及五水平正交表L25(56)等。