e=ac=||FO2FB22||=cos∠OF2B2.
(4)若椭圆的标准方程为ax22+yb22=1(a>b>0),则椭圆与 x 轴的交点 A1,A2 到焦点 F2 的距离分别最大和最小,且|A1F2|=a+c,|A2F2| =a-c.
精选ppt
15
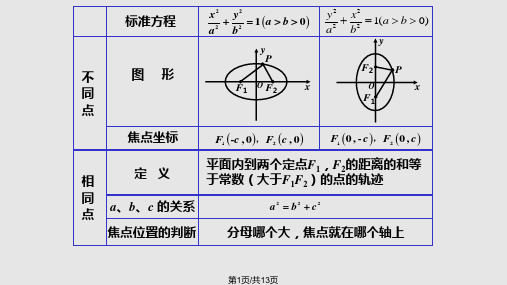
思考:已知椭圆的长轴A1A2和短轴B1B2 ,
怎样确定椭圆焦点的位置?
知椭圆的标准方程,则根据a、b的值可确定其性质.
(2)明确a,b的几何意义,a是长半轴长,b是短半轴长,不
要与长轴长、短轴长混淆,由c2=a2-b2,可得“已知椭圆
的四个顶点,求焦点”的几何作图法,只要以短轴的端点
B1(或B2)为圆心,以a为半径作弧交长轴于两点,这两点就 是焦点.
精选ppt
14
(3)如图所示椭圆中的△OF2B2 找出 a,b,c, e 对应的线段或量为 a=|F2B2|,b=|OB2|,c=|OF2|,
B2
a
A1
F1 c
b
oc
a
A2
F2
因为a2=b2+c2,所以以椭圆B1 短轴端点为
圆心,a长为半径的圆与x轴的交点即为
椭圆焦点.
精选ppt
16
4 离心率
思 考观 察 不 同 的 图2椭 .1圆 9,我 们 发, 现
椭 圆 的 扁 平 程 ,那度么 ,用 不什 一么 量 可 以 画 椭 圆 的 扁 平 ? 程 度 呢
18
我们把椭圆的焦 轴距 长与 c的称 长为椭: 圆的离心率
用e来表示, e即 c.
a
a
因为 a >c>0,所以 e 的取值范围是:__0_<_e_<_1___
e 越接近于1,则c越接近于a,从而b就越小,因此椭圆就 越扁反之,e越接近于0, c 就越接近于0,从而b 就越接近 于 a,这时椭圆就越接近于圆