当前位置：文档之家 › 简谐振动教程(详细)

简谐振动教程(详细)

  • 格式：ppt
  • 大小：619.50 KB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

大学物理简谐运动

大学物理简谐运动


t
t2
t1
x
A
a
b
Ab
A2
t
x
o
A
v
π
A
t π 3 T 1 T
0
A 2
Aa
A
3
2π 6
二 旋5 转– 1矢简谐量运动 简谐运动的振幅 周期 频率和相位
物理学教程 （第二版）
2）对于两个同频率的简谐运动，相位差表示它们间步调 上的差异.（解决振动合成问题）
x1 A1 cos(t 1) x2 A2 cos(t 2 )
物理学教程 （第二版）
x t 用旋转矢量图画简谐运动的
图
x A
x x Acos(t ) π
A
4
*
*
**
O
t O * T T * 3T T 5T
4* 2* 4
4
-A
-A
*
T 2π （旋转矢量旋转一周所需的时间）
二 旋5 转– 1矢简谐量运动 简谐运动的振幅 周期 频率和相位
x t 用旋转矢量图画简谐运动的
3 简5谐– 运1 简动谐的运动能简量谐运动的振幅 周期 频率和相位
物理学教程 （第二版）
例 质量为 0.10kg 的物体，以振幅 1.0102 m 作简谐运
动，其最大加速度为 4.0m s2，求：
（1）振动的周期；
解:
amax A 2
amax 20s1
A
T 2π 0.314s
（2）通过平衡位置的动能；
Ep 1.0103J
由
Ep
1 2
k x2
1 2
m 2 x2
x2
2Ep
m 2
0.5104 m2
简谐振动教程

简谐振动教程

简谐振动教程简谐振动是自然界中一种常见的振动现象，特点是周期性、方向性固定、振幅可变。

简谐振动广泛应用于物理、工程和生物等领域，以下是一份详细的简谐振动教程。

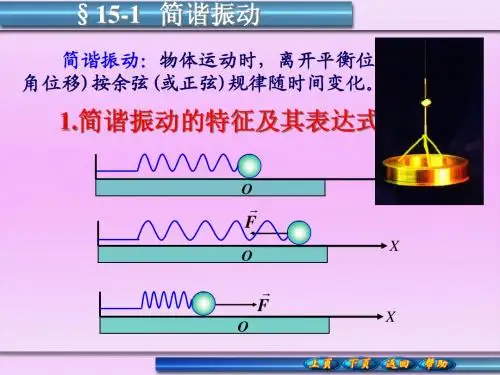
一、简谐振动的基本概念简谐振动是指一个物体在弹性力的作用下以一定振幅沿着其中一方向周期性地来回振动的现象。

简谐振动具有如下特点：1.周期性：物体完成一次完整的振动所需的时间为周期，记作T。

2.频率：频率是指单位时间内完成的振动次数，记作f，单位是赫兹（Hz），即1Hz等于一秒内完成一次振动。

3.振幅：振幅是指物体振动时与平衡位置之间的最大位移距离。

二、简谐振动的数学描述简谐振动可以用数学函数来表示，常用的数学表示方式有正弦函数和余弦函数。

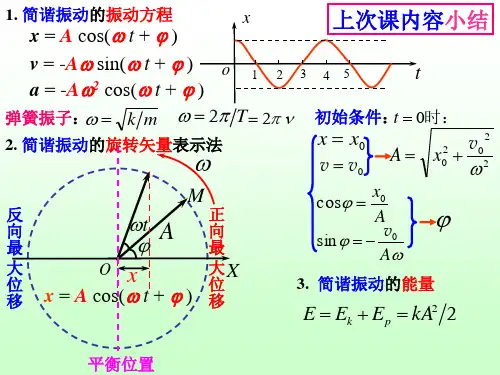
一般来说，振动方程可以写成如下形式：x(t) = A*cos(ωt + φ)其中，x(t)表示物体在时刻t的位移，A表示振幅，ω表示角频率，φ表示初相位。

三、简谐振动的运动规律1.位移与时间的关系：位移与时间的关系可以通过振动方程来描述。

根据振动方程可知，位移随时间的变化是呈正弦或余弦函数的周期性变化，即做正弦或余弦曲线。

2.速度与时间的关系：速度是位移对时间的导数，即v(t) = dx(t)/dt。

可以通过对振动方程进行求导得到速度与时间的关系式。

3.加速度与时间的关系：加速度是速度对时间的导数，即a(t) = dv(t)/dt。

同样可以通过对振动方程进行求导得到加速度与时间的关系式。

四、简谐振动的特性1.周期与频率的关系：周期T与频率f之间存在如下关系：T=1/f。

也就是说，周期和频率是互为倒数的。

2.能量守恒：简谐振动的系统中，振动能量在运动过程中是守恒的，由动能和势能相互转化。

振动系统的总能量等于振动质点的动能和势能之和。

在振幅不变的情况下，位移越大，动能越大，对应的势能越小。

3.振动的相位差关系：对于同一简谐振动系统中的两个质点，其相位差等于时间差乘以角频率。

两个质点的位移相差一个相位差，相位差的大小可以通过两个质点的位移波形图来确定。

大学物理简谐振动

大学物理简谐振动

tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
A2
A
A2 sin 2
2 -1
2
O
1 A1 x2
A1 sin 1
x2 x
x1x1
x2
x
A1 cos1 A2 cos2
合振动振幅：A A12 A22 2A1A2 cos(2 1)
1. 两个分振动的相位相同（同相）
5 (或 3 )
4
4
第六章
机械波
mechanical wave
6.1 机械波的产生、传播和描述 波动: 振动在空间中的传播过程.
机械波: 机械振动在弹性介质中的传播过程. 波动
电磁波: 交变电磁场在空间中的传播过程. 6.1.1 机械波的产生
当弹性介质中的一部分发生振动时，由于介质各个 部分之间的弹性力作用，振动就由近及远地传播出去. (1) 机械波实质上是介质中大量质点参与的集体振动;
20 0.47
(2) 30为何值时, x1+x3 的振幅为最大; 30为何值时, x2+x3的振幅为最小.
x1 0.05cos10t 3 4
x2 0.06cos10t 4
x3 0.07 cos10t 30
30
10
0 时，x1+x3 振幅最大：30
10
3
4
30 20 时，x2+x3 振幅最小：30 20
t 时刻点 P 的振动状态
P点在
t
时刻的位移
y P ,t
yO ,t x
u
A c os [ (t
x) u
0 ]
波函数 (波方程)
y( x, t )
A cos[ (t
简谐振动

简谐振动


1 1 2 2 2 2 m A sin (t 0 ) kA cos 2 (t 0 ) 2 2
简谐振动的能量
1 2 考虑到 k m ，系统总能量为 E kA ，表明 2 简谐振动的机械能守恒。
2
能量平均值
1 T1 1 2 2 2 2 EK m A sin (t 0 ) d t kA T 0 2 4
§15-1 简谐振动
简谐振动：物体运动时，离开平衡位置的位移(或 角位移)按余弦(或正弦)规律随时间变化。
1.简谐振动的特征及其表达式
O
X
F
X
O
F
O
X
简谐振动的特征及其表达式
位移 x 之解可写为： 或
x A cos(t 0 )
i(t 0 )
x Ae
简谐振动的运动学特征:物体的加速度与位移成正 比而方向相反，物体的位移按余弦规律变化。
1 T1 2 1 2 2 EP kA cos (t 0 ) d t kA T 0 2 4
EK EP E 2
上述结果对任一谐振系统均成立。
简谐振动的能量
谐振子的动能、势能和总能量随时间的变化曲线:
E
EP
1 2 E kA 2
O
Ek
t
x
O
x A cos t
t
简谐振动的振幅、周期、频率和相位
(3)相位和初相
相位 (t 0 ) ：决定简谐运动状态的物理量。
初相位 0 ：t=0 时的相位。 相位概念可用于比较两个谐振动之间在振动 步调上的差异。 设有两个同频率的谐振动，表达式分别为： x1 A1 cos(t 10 )
x2 A2 cos(t 20 )
简谐震动简正坐标(0301)

简谐震动简正坐标(0301)

声学
在声学领域，声音的传播和辐射都 可以看作是简谐震动的叠加，因此 简谐震动理论也是声学研究的重要 基础。
02
简正坐标的概念
什么是简正坐标
• 简正坐标是一种描述系统振动的坐标方式，它将复 杂的振动问题简化为简单的数学模型，以便于分析 和求解。在简正坐标下，系统的振动形式被分解为 一系列正弦和余弦函数，每个函数代表一种独立的 振动模式。
简谐震动
简谐震动是物理学中一个基本而重要的概念，它描述的是一个振动系统在平衡 位置附近做周期性的往复运动。简谐震动可以用数学公式表示，其运动规律具 有特定的周期性和振幅。
简正坐标
简正坐标是用来描述简谐震动的坐标系，它能够将复杂的振动问题简化，方便 分析和计算。简正坐标系的选择取决于系统的具体形式和物理特性。
实例二：单摆的简谐震动
总结词
单摆在摆角较小的情况下，做近似于简谐振动的往复运动。
详细描述
单摆由一根长度为摆长的细线悬挂着一个质量块组成，在重 力作用下产生往复运动。当摆角较小（小于5度）时，单摆的 运动可以近似看作是简谐振动。在简正坐标系下，单摆的振 动形式可以表示为正弦或余弦函数。
实例三：电磁振荡器的简谐震动
教育教学
在高等教育中，简谐震动和简正坐标是物理学、工程学等专业的重要教学内容。通过深入 学习和理解简谐震动和简正坐标的理论基础，可以培养学生的逻辑思维和分析能力，提高 他们的科学素养。
THANKS
感谢观看
简正坐标的应用
1. 振动分析
简正坐标广泛应用于振动分析 领域，用于研究系统的振动特
性和响应。
2. 结构优化
在结构优化设计中，简正坐标 可以帮助分析结构的振动模态 和频率，从而优化结构的设计 。
3. 声学研究
第九章第一节 简谐运动

第九章第一节 简谐运动

二、简谐运动
振子以O点为中心在水平杆方向做往复运动。振子由A点开始运动，经过O点运动到A’点，由C 点再经过O 点回到A 点，且OA 等于OA’ , 此后振子不停地重复这种往复运动。以上装置称为弹簧振子。
1）回复力
振子在振动过程中，所受重力与支持力平衡，振子在离开平衡位置 O 点后，只受到弹簧的弹力作用，这个力的方向跟振子离开平衡位置的位移方向相反，总是指向平衡位置，所以称为回复力。
MOMODA POWERPOINT
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Fusce id urna blandit, eleifend nulla ac, fringilla purus. Nulla iaculis tempor felis ut cursus.
第九章 机械振动
第一节 简谐运动
一、机械振动
物体（或物体的一部分）在某一中心位置两侧所做的往复运动，就叫做机械振动。
钟摆的摆动 担物行走时扁担的颤动 风中飘扬的红旗 秋千 振动的音叉、鼓 地震等都是机械振动。
比如：
振动是自然界广泛存在的，一般的振动往往都比较复杂，所以我们先研究最简单、最基本的振动，这种振动叫简谐振动
3）简谐运动的特点 （１）周期性：每经过一个周期，物体运动的速度、位移、加速度均与一个周期前相同。经过半个周期与半周期前相比，物体的位移、速度、加速度大小相等方向相反。 （２）对称性：简谐运动物体运动到同一点或关于平衡对称的两点时，其位移、速度、加速度均大小相等。 （３）矢量性：注意位移、速度、加速度均为矢量，相同时必须是大小方向均相同。 （ 4 ）简谐运动是一种非匀变速运动 （ 5 ）简谐运动是一种理想化的运动，振动过程中无阻力，所以振动系统机械能守恒。
振动力学教程PPT课件

振动力学教程PPT课件


动的叠加-----------谐波分析
•
2、非周期：利用傅立叶积分作谐波分析
• δ函数又称为单位脉冲函数-----它的性质、应用
示成一系列简谐振
第22页/共35页
第一节：简谐振动及其表示方法
•一、简谐振动的表示方法
• （一）正弦函数表示
2、A、ω、Φ ------简谐振动三要素
第23页/共35页
第24页/共35页
船舶的模态分析和强度分析，飞行器的结构振动和声疲劳分析等。
3） 在土木建筑、地质工程中：建筑、桥梁等结构物的模态分析，地震
引起结构物的动态响应，爆破技术的研究等。
4） 在医学、生物工程中：脑电波、心电波、脉搏波动等的信号处理等。
第12页/共35页
2途径：
1）从具体的工程对象提炼出力学模型 2）建立数学模型------应用力学知识建立所研究问题的数学模型 3）对数学模型进行分析和计算，求出请确、近似或数值解。 4） 比较------将计算结果与工程问题的实际现象或实验研究的测试结果进行 比较，考察理论结果是否解决该工程问题，如不能解决而数学模型及求解均无错 误，则需要修改力学模型重复上述过程。
第9页/共35页
5 随机振动
20世纪50年代，航空和航天工程的发展对振动力学提出了更高 的要求，确定性的力学模型无法处理包含随机因素的工程问题----如大气湍流引起的飞机颤振、喷气噪音导致飞行器表面结构 的声疲劳、火箭运载工具有效负荷的可靠性等。工程的需要迫使 人们用概率统计的方法研究承受非确定性载荷的机械系统和结构 的响应、稳定性和可靠性等， 从而 形成了随机振动这一振动力 学的重要组成部分。 在工程问题中振动信号的采集和处理是随机振动理论应用的前提， 由于计算机的迅速发展和快速第1傅0页/立共35叶页 变换算法的出现，随机振动
简谐振动(单摆)

简谐振动(单摆)


• 析：设将摆提至最大偏 后释放，当摆至偏角 为 时，角速度为 ，根据机械能守恒定律有：
• 而对没有凹槽的一般单摆有：
• • 因此该振动系统的周期为
• 例5. 用一根长为L的细绳将一个密度
的小球
拴在盛水的容器底上，如图1所示。若使小球稍微偏
离平衡位置而振动起来，它的周期将是多少？（水的
阻力不计）
能力·思维·方法
【解析】(1)振幅为最大位移的绝对值，从图像可 知振幅A=5cm. (2)从图像可知周期T=0.8s，则振动的频率： f=1/T=1/0.8=1.25Hz. (3)由各时刻的位移变化过程可判断：t=0.1s、 0.7s时，质点的振动方向向上； t=0.3s，0.5s时，质点的振动方向下.
能力·思维·方法
【例3】将某一在北京准确的摆钟，移到南 极长城站，它是走快了还是慢了?若此钟在 北京和南极的周期分别为T北、T南，一昼夜 相差多少?应如何调整?
能力·思维·方法
【解析】单摆周期公式T= 2 l ，由于北京和南极
g 的重力加速度g北、g南不相等，且g北＜g南，因此 周期关系为：T北＞T南.
单摆简谐运动的图像
要点·疑点·考点 课前热身 能力·思维·方法 延伸·拓展
要点·疑点·考点
1.单摆
(1)单摆：一条不可伸长的、忽略质量的 细线，一端固定，另一端拴一质点，这样构 成的装置叫单摆.
这是一种理想化的模型，实际悬线(杆)下接 小球的装置都可作为单摆.
(2)单摆振动可看作简谐运动的条件是最 大偏角α＜5°.
(5)单摆的等时性：在小振幅摆动时，单摆的 振动周期跟振幅和振子的质量都没关系.
要点·疑点·考点
2.简谐运动图像 (1)物理意义：表示振动物体的位移随时间变化
(24)简谐振动1绪论、概念、特征方程、特征量、旋转矢量法new.

(24)简谐振动1绪论、概念、特征方程、特征量、旋转矢量法new.

【课时】3-4次课
简谐运动（1）绪论、概念、特征方程、特征量、旋转矢量法
力学量（如位移）
机械振动
一物理量在某一定值附近周期性变化的现象称振动。 机械振动 电磁振动
电磁量（如I 、V、 E、 B） 机械振动 物体围绕一固定位置往复运动.
其运动形式有直线、平面和空间振动.
例如一切发声体、心脏、海浪起伏、地震以及晶体 中原子的振动等. 最基本、 最简单、最重要的振动是简谐振动。 简谐运动
思考：加入改变原点位置， 结果如何？
P ( M m )g
F合 （M m ) g k( L l x ) kx 为简谐振动 d 2x 由 ( M m) 2 kx 得 dt 2 d x k d2x 2 为简谐振动 x 0 x 0 即 2 M m dt dt2
注意
T 2π
m k
周期和频率仅与振动系 统本身的物理性质有关
简谐运动（1）绪论、概念、特征方程、特征量、旋转矢量法
简谐运动中， x和 v 间不存在一一对应的关系.
机械振动
x A cos(t ) v A sin(t )
（三）相位
A
x
o
A
v
v
T 2
xt 图
2. 描述简谐振动的特征量 （一） 振幅
机械振动
A xmax
A
x xt 图
T 2
T
（二）
A x A cos(t ) A cos[ (t T ) ]
周期
周期、频率
o
t
1 频率 T 2π 2π 圆频率 2π T
T
2π
弹簧振子周期
1. 简谐振动的运动学方程
简谐运动

简谐运动


准弹性力
系统本身决定的常数
动力学方程：
在水平方向上：
弹簧振子
F kx
由牛顿第二定律
d 2x kx m 2 dt
k 令 2 m
则有
d x 2 x 0 2 dt
二阶齐次常 微分方程
2
一般写成： 或：
x A sin t x A cost
振动和波动
共同特征：运动在时间、空间上的周期性
振动: 任何物理量在某一定值附近随时间周期性变化
波动: 振动在空间的传播
振动
机械振动：物体在某一位置附近作周期往复运动 电磁振荡：电场、磁场随时间作周期性变化
简谐振动（简谐运动）：最简单、最基本的振动
9-1简谐振动
一、简谐振动的基本特征
弹簧振子
轻弹簧 k + 刚体 m (平动~质点） 集中弹性 集中惯性
解得
2 2 v v 2 A x0 02 x 2 2
的状态如何就决定了系 统未来的振 但计算A的大小时不一定非用初 始 条件，只要同时告诉某 时刻的x与
幅A的大小。所以A由初始条件决定。
相应的v，又知道，就可以求出A。
3、初相位
初相：
由 t = 0时
x0 A cos v0 A sin
(1)、相位 t 是确定振动状态的物理量
(2) ( t )与状态参量 x，v有一一对应的关系
x A cos(t ); v A sin(t )
当 t 例：

3
时：
A x , 2
A x , 2
3 v A 2
质点在 x A 2 处以速率 v向 x方向运动
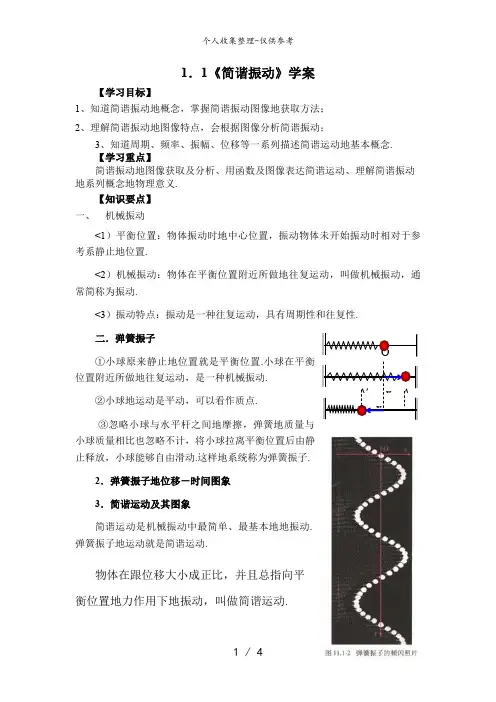
1.1《简谐振动》教案(鲁科版选修3-4)

1.1《简谐振动》教案(鲁科版选修3-4)

1．1《简谐振动》学案【学习目标】1、知道简谐振动地概念，掌握简谐振动图像地获取方法；2、理解简谐振动地图像特点，会根据图像分析简谐振动；3、知道周期、频率、振幅、位移等一系列描述简谐运动地基本概念.【学习重点】简谐振动地图像获取及分析、用函数及图像表达简谐运动、理解简谐振动地系列概念地物理意义.【知识要点】一、机械振动<1）平衡位置：物体振动时地中心位置，振动物体未开始振动时相对于参考系静止地位置.<2）机械振动：物体在平衡位置附近所做地往复运动，叫做机械振动，通常简称为振动.<3）振动特点：振动是一种往复运动，具有周期性和往复性.二．弹簧振子①小球原来静止地位置就是平衡位置.小球在平衡位置附近所做地往复运动，是一种机械振动.②小球地运动是平动，可以看作质点.③忽略小球与水平杆之间地摩擦，弹簧地质量与小球质量相比也忽略不计，将小球拉离平衡位置后由静止释放，小球能够自由滑动.这样地系统称为弹簧振子.2．弹簧振子地位移－时间图象3．简谐运动及其图象简谐运动是机械振动中最简单、最基本地地振动.弹簧振子地运动就是简谐运动.物体在跟位移大小成正比，并且总指向平衡位置地力作用下地振动，叫做简谐运动.写出F＝-kx说明式中F为回复力；x为偏离平衡位置地位移；k是常数，对于弹簧振子，k是劲度系数，对于其他物体地简谐运动，k是别地常数；负号表示回复力与位移地方向总相反.质点地位移随时间按正弦规律变化地振动，叫做简谐运动.简谐运动地位移－时间图象为正弦曲线.【典型例题】例1、如图所示，在光滑水平面上，用两根劲度系数分别为k1、k2地轻弹簧系住一个质量为m地小球，开始时，两弹簧均处于原长，后使小球向左偏离x后放手，可以看到小球将在水平面上作往复振动，试问小球是否作简谐运动？分析：为了判断小球地运动性质，需要根据小球地受力情况，找出回复力，确定它能否写成F=-kx地形式.解读：以小球为研究对象，竖直方向处于力平衡状态，水平方向受到两根弹簧地弹力作用，设小球位于平衡位置O左方某处时，偏离平衡位置地位移为x，则左方弹簧受压，对小球地弹力大小为F1=k1x，方向向右.右方弹簧被拉伸，对小球地弹力大小为F2=k2x方向向右.小球所受回复力等于两个弹力地合力，其大小为F=F1+F2=(k1+k2>x，方向向右，令k=k1+k2，上式可写成F=kx 由于小球所受回复力地方向与位移x地方向相反，考虑方向后，上式可表示为F=-kx所以，小球将在两根弹簧地作用下，沿水平面简谐运动.说明：由本题可归纳出判断物体是否作简谐运动地一般步骤：确定研究对象<整个物体或某一部分）→分析受力情况→找出回复力→表示成F=-kx地形式<可以先确定F地大小与x地关系，再定性判断方向）.【达标训练】1．做简谐运动地质点，先后经过同一点时，下列物理量哪些是不同地< ）A．速度 B．加速度 C．位移 D．动能OBC 2．某个弹簧振子在水平方向上做简谐运动，下列说法中正确地是< ） A ．该振子地加速度和位移大小成正比，方向相反 B ．该振子地加速度和位移大小成正比，方向相同 C ．该振子做非匀变速运动D ．该振子做匀变速运动3．弹簧振子做简谐运动时，下列说法中正确地是< ） A ．若位移为负值，则速度一定为正值B ．振子通过平衡位置时，速度为零，加速度最大C ．振子每次通过平衡位置时，加速度相同，速度也相同D ．振子通过同一位置时，速度不一定相同，但加速度一定相同 4．如图，一水平弹簧振子，O 为平衡位置，振子在B 、C 之间做简谐运动，设向右为正方向，则振子< ）A ．由C 向O 运动时，位移为正值，速度为正值，加速度为正值B ．由O 向B 运动时，位移为正值，速度为正值，加速度为负值C ．由B 向O 运动时，位移为负值，速度为正值，加速度为负值D ．由O 向C 运动时，位移为负值，速度为负值，加速度为正值5．水平方向做简谐运动地物体偏离平衡位置地位移为X ，速度为V ，加速度为a ，则< ）A ．X 与V 同向时，物体加速B ．X 与V 反向时，物体加速C ．V 与a 同向时，位移变大，D ．V 与a 反向时，位移变大6．关于水平方向上做简谐运动地弹簧振子地位移，加速度和速度间地关系，下列说法中正确地是< ）A ．位移减小时，加速度减小，速度增大B ．位移地方向 总是跟加速度地方向 相反，跟速度地方向相同C ．振子地运动方向 指向平衡位置 时，速度地方向 跟位移方向相同D ．振子地运动方向改变时，加速度地方向也改变7．如图，若水平弹簧振子在B 、C 间做简谐运动，O 点为平衡位置，则< ） A ．振子在经过O 点时速度最大，回复力也最大 B ．振子在经过O 点时速度最大，回复力为零C ．振子在由C 点向OOBC加速度却逐渐增大D．振子在由O 点向B点运动地过程中，弹性势能逐渐增大，加速度却逐渐减小，则在位移8．若做简谐运动地弹簧振子地振幅是A，最大加速度地值为amX=A/2处振子地加速度值a=.答案:申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途.。

3.1 简谐振动


例 一物体沿x轴做简谐振动，平衡位置在坐标原点O， 振幅 A 0.12m，周期 T 2s。当t=0时，物体的位 移 x 0.06m，且向x轴正方向运动。求： (1) 简谐振动的表达式； 解： x Acos( t ) 已知A 0.12m，T 2

2s
1 cos = ， = 当t 0时，x 0.06m 2 3 t 0时，v0 A sin 0 = 3
第7章 机械振动
x
x0
x
3.1 简谐振动
讨论
1）对同一简谐运动，相位差可以给出两运动状 态间变化所需的时间.
x A cos(t1 ) x A cos(t2 )
(t2 ) (t1 ) t t 2 t1
第7章 机械振动
它的大小由振动系统的初始状态决定。
约定：
( π,π]
第7章 机械振动
3.1 简谐振动
讨论 初始条件确定 A 和 ：
x A cos(t )
t 0 t 0
x v
x0 A cos
v0 A sin
A x0
2
v
v0 tan x0
谐振动物体的振动速度
谐振动物体的振动加速度
dv a A 2 cos(t ) dt
第7章 机械振动
3.1 简谐振动
x A cos(t )
取 0
A
o o
A
x
x t 图
T
t
t
v A sin(t )
A
v
a
v t 图
T
π A cos(t ) 2

第一章(简谐振动)(3-4)

2 2
2
2
2、频率不同的两个简谐振动的 合成不再是简谐振动，振动比为 有理数时，合成为周期振动；频 率比为无理数时，合成为非周期 振动。
•1、证明：
•1、证明：
• • • • •
设T=mT1=nT2，记x=x1+x2，则： x(t+T)=x1(t+T)+x2(t+T) = x1(t+mT1)+x2(t+nT2) =x1(t)+x2(t) =x(t)
• 两张频谱图中的图形都是离散的直线，称为谱 线，各种分量的幅值及相位角如何一目了然， 这种分析振动的方法称为频谱分析 • 考虑的自变量由时间改变为频率，所以频谱分 析实际由时间域转入频率域
虽然周期振动的谐波分析以无穷级数出现， 但一般可以用有限近似表示周期振动
对称函数与反对称函数相乘在 区间积分应为零
J c J 0 ml 2
69
例 2.3 一个质量为m的物体从h高处自由落下， 与一根抗弯刚度为EJ、长L的简支梁作完全非弹 性碰撞，不计梁的质量，求梁的自由振动的频 率和最大挠度。
M
x
70
解：
由材料力学可知简支梁在 重物mg作用下的静变形为： m gl3 s 48EJ
M
x
故自由振动频率为： wn
mg k (s x) m x
52
在静平衡时有：
m g ks
代入：
mg k (s x) m x
振动微分方程为：
kx m x
令 k / m g / s
2 n
n2 x 0 x
方程的通解为：
x A sin(nt )
狄里赫利条件

第十三章(振动一讲)

演示
T
t( s)
( 2)相轨迹 ( 相图) x v图线. x A cos(0t )
v A0 sin(0 t ) 2 v 2 2 得: x 2 A
由
v x o
11
0
四、简谐振振动的矢量表示法 vm 0 A 如图:振幅矢量 A 以圆频 v0 率 0 绕平衡点 o 逆时针 A( t ) 方向转动 . 2 an A0 A( t 0) A在x轴上的投影点运动, 0t 0 表示一特定的简谐振动.
0 t 0 t t 0 初相位
8
注意：相位是相对的； 同相、反相； 超前、落后。
例如,二同频率不同振幅的谐振动:
x1 A1 cos(0t 1 ) x2 A2 cos(0t 2 )
t时刻的相位差:
相位
1 0t 1
2 0t 2
t时刻 :
x A cos(0t )
k 0 m
例题1.设一物体沿x轴做简谐振动，振幅为12cm， 周期为2.0s；在t=0时的位移为6.0cm，且这时物 体向x正向运动。试求： (1) 初相位、振动方程; (2) t =0.5s时物体的位置、速度和加速度； (3) 在 x=-6.0cm处，且向x负向运动时，物体的速 度和加速度，以及它从这个位置到达平衡位置所 用的时间。 [解] A 0.12m , 0 2 T 5或 据题意设物体的运动方程为 A 3 A 2 x 0.12 cos( t ) 0 x 则t 0时刻 : 0.06 0.12cos 3 A 14 而v 0.12 sin 0, 故 3 0
(3) 在x=-6.0cm处，且向x负向运动时，有 0.06 0.12cos( t 3)

简谐振动


3
1. 简谐振动（Simple Harmonic Motion）
x Acos( t ) →运动学判据
即:按时间t的余弦或正弦函数描述的运动
x 可作广义理解（位移、电流、场强、温度…） 简谐振动是最简单、最基本的振动，可用来研究 复杂的振动。
F kx →动力学判据
d2x dt 2
时，振幅矢量转过的角度为： 5
t 0.83(s)
26

21
例：一质点作简谐振动，其振动曲线如图所示。根
据此图写出该振动的表达式。 x(cm)
解：由振动曲线可知：A 0.04 4
由振动曲线可得t＝0和t＝
o
2对应的旋转矢量如图
2
2
t(s)
对应的相位：
t＝2
cos2 (t
)
因 此 ，弹 簧 振 子 的 总 机 械 能 为:
E

Ek

Ep

1 2
kA2
结论：（1）作简谐运动的物体，其机械能守恒。
（2）简谐运动的总能量和振幅的平方成正比。
9
5.其它简谐振动 例如单摆
取逆时针为 张角正向，以悬
点为轴，重力的切向分量
Ft mg sin
“ – ”表示力与 张角方向相反。
设振动物体在任一时刻t 的位移为x ，速度为v ，于是
它所具有的动能EK 和势能EP 分别为
Ek

1 2
mv2
Ep

1 2
k x2
考虑到 x Acos(t ) 及v Asin(t )与2 k / m

Ek
1 kA2 sin 2 (t )
2

大学物理-12第十二讲简谐振动的合成、阻尼、受迫振动（001）


解得 ω = ωr = ω02 − 2β 2
则
A=
2mβ
F0
ω02 − β 2
= Amax
A
β2 β3
β1
ω
β1 > βω2 0> β3
23
2.速度共振—使速度振幅达最大值的状态
v = dx = − Aω sin(ωt − δ )
dt
速度振幅 vm = Aω
而 Aω =
F0ω
m (ω02 − ω2 ) + 4β 2ω2
●合振幅A的大小由两个分振动的初相差决定。
当 Δϕ = ϕ2 − ϕ1 = ±2kπ
(k = 0，1，2") 同相
Y ωK
A2
ωK
A ωK
A = A1 + A2 = Amax
θ2
Δθ θ1
A1
合振动加强
x2 θ x1 x x
4
当 Δϕ = ϕ2 −ϕ1 = ±(2k +1)π 反相
(k = 0，1，2")
ϕ =0
t
19
2. β =ω0（临界阻尼） x = e −βt (C1 + C 2t)
●在临界阻尼时，质点到达平衡位置时速度即减为 零，振动不可能发生。
◆原理常用于阻尼天平等，以减少摆动时间.
3. β >ω0（过阻尼）
x = e − βt (C 1e ω1t + C 2 e −ω1t )
●过阻尼时，质点的速度 x
F强 = F0 cosωt
v = dx = Aω cos ωt v与强迫力同位相。
dt
●在整个周期内外力的方向和物体运动方向一致， 不断对物体作正功，使振动最强。 ◆外力的周期性变化与物体的固有振动“合拍”。

简谐振动方程的求解方法

简谐运动的位移x=Rcos（ωt+φ）；
简谐运动的速度v=-ωRsin（ωt+φ）；
简谐运动的加速度a=-ω2Rcos（ωt+φ），上述三式即为简谐运动的方程。

扩展资料
简谐运动的特点
一、物体运动的路线不一定都是直线
例如，单摆摆球做简谐运动时的运动路线是在摆球平衡位置两侧并通过平衡位置的一段圆弧，即摆球的运动路线为曲线。

二、物体运动的速度方向与位移方向不一定相同
简谐运动的位移指的是振动物体偏离平衡位置的位移，位移的起点总是在平衡位置，那么当物体远离平衡位置时位移方向与速度方向相同，靠近平衡位置时位移方向与速度方向相反。

三、振动物体所受的回复力方向与物体所受的合力方向不一定相同
例如，单摆在平衡位置附近（小角度范围内）的摆动既做圆周运动，又做简谐运动，摆球所受到的各个力的合力既要提供其做圆周运动的向心力，又要提供其做简谐运动的回复力，即单摆振动过程中摆球受到所有力的合力的一个分力提供向心力，另一个分力提供回复力。

那么回复力方向就与摆球所受到的各力的合力方向不相同。

四、物体在平衡位置不一定处于平衡状态
例如，单摆摆球做简谐运动经过平衡位置时，由于摆球的平衡位置在圆弧上，摆球在圆弧上做圆周运动需要向心力，故摆球在平衡位置处悬绳的拉力大于摆球的重力，即摆球在平衡位置并非处于平衡状态。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a dv 2 A cos t 2 x dt
12
v、x 哪个超前？
x A1 A2 O - A2 -A1
x2
x
x1
同相
T t
A1 A2 O - A2 -A1
x1
反相
T t
x2
x
A1 A2
x1
O
- A2 -A1
x2
t x2超前于x1
13
3.旋转矢量表示法： 旋转矢量A 注意影子
机械振动 一、简谐振动
§1 简谐振动的动力学方程 §2 简谐振动的描述 §3 简谐振动的能量
二、简谐振动的合成
1
1. 振动：
平衡位置附近作周期性 来回往复的运动。 振动的成因是回复力。 平衡位置的回复力总为零。 振动的基本形式—简谐振动
oscillation
x
t
钟摆、活塞、波浪、 琴弦、交流电、 脑电波、生物钟
二者的相位差为：
(t 20 ) (t 10 ) 20 10
11
由 2.振动曲线： x A cos t 描点
v
x
a
t
相差？
*速度和加速度： dx v A sin t A cos t 2 dt
kx m g
kx kx kx kx
d 2 2 k k x x0 2 dt m m
得证
F mg k ( x x)
d 2x k a kx x 0 m 2 dt m
2 m T m k
k
6
4、简谐方程的、A和
1）固有圆频率取决于振子本身固有性质
A

t=5/6 ( s)
x
2 T t
2 2 5 / 6 t

x t=0( s)
t=5/6 （ s）22
§3 简谐振动的能量
1 Ek m 2 A2 sin 2 t 2
1 E p m 2 A2 cos2 t 2
投影到任意轴？

A
φ
x
x A cost
投影到X轴, 描述X方向的谐振动
x
Y
14 投影到Y,描述Y方向的谐振
旋转矢量与振动的对应量
Rotational vector and phase

t
A
φ
t0
相差？

x

t
对应量 旋转矢量 简谐振动 A 长度 振幅 φ 初角 t+φ 夹角 位相 x 投影 位移 15 角速度
解：
A2
A
A 1
A 22 42 2 5
o
.464 x 2 5 cos3t 026.6O

x
tg 1

26.6 0.464 180
2 4
27
小结 谐振
F kx summary2 x brief a d 2x 2x 0 2 dt x A cost
A cos t
合成后仍然是谐振。式中A和为：
24
x A cost
A
2 A12 A2 2 A1 A2 cos 2 1
A1 sin 1 A2 sin 2 tg A cos A cos 1 2 2 1
8
EX.待物体静止后,再向下拉 Y y0=0.1m后放手,测得T=2s。 O 求：振动方程.
解： 2 s 1 T y0 0.1 v 0 0
2 A y0
0.1m

Y
2
2 v0
y0 0.1m
v 0 舍 tg1 0 y y 0 0 0
Ⅰ.谐振特点 Ⅱ.谐振描述 x-t曲线 几何表示 旋转矢量
振动方程x =Acos( t+φ )（单位）
1 Ek E p EM kA 2 Ⅲ.机械能守恒 2 Ⅳ.同方向同频率的谐振动合成
28
1
2 1 2k 2 1 2k 1
A A1 A2
A A1 A2
25
2. 旋转矢量法：
A2
x2 2 1
A A1
x x1 x2
x
x1
x1 x
3、振动曲线法：
x2
26
t
Ex.
已知：
x1 4 cos3t
x2 2 cos 3 t 2 写合振动方程。
负号表示指向平衡位置，得证。
正
方
向
f
mg
由f=mat=ml
d 2 m l 2 m g dt d 2 g 0 dt 2 l l T 2 令2=g / l g
m cost
5
EX.证明悬挂的弹簧m,k的振 动是谐振。求出振动周期。
o
O
x
x
解：弹簧原长处为o’ 平衡位置O 任意x处
1 1 E m 2 A2 kA2 2 2
E
Ep
Ek
23
t
简谐振动的合成
同方向同频率的谐振合成
1 .运动学方程法 x1 A1 cos t 1 x2 A2 cos t 2 x x1 x2 A1 cost 1 A2 cost 2
方法一：用t=0时的旋转矢量 x(m) x(m)
0.02 0.02
t (s) 4
19
方法二：先参考标准式 x 0.02cos t m
2
再根据初相平移 x 0.02 cos( t )m 2 2 x(m) t (s)
20
21
例10-1 一质点沿x轴作简谐振动，A=0.12m T=2s，x0=0.06m,此时刻质点向x正向运动。 求:(1)振动方程 (2)t=T/4时x,v,a (3) 第一次通 过平衡位置的时刻t 和所需时间t。
解： 2
T
(3) 第一次通过平衡位置的时刻t
3
(1) x=Acos(t+φ) =0.12cos(t ) m (2) v=Acos(t +/2) m/s a=Acos(t +) m/s2 把t=T/4 代入x,v,a
振动 方程：

O
0.1m
y 0.1cos t
m
9
§2 简谐振动的描述
简谐振动 — x随t按正弦或余弦变化 三种描述方法： 1.振动方程：x A cost
单位
—圆频率—2秒内的振动数。 2 s 1 t +φ—相位—反映质点的运动状态(x,v)。 10
圆频率 初位相
思考: 在旋转矢量图上怎样表现位相 超前或落后、相差、 同相、反相？

2 1
o
x
2 1

x
2 1
o
o
16
x
例1. 按图写振动方程。x 10 cos( ห้องสมุดไป่ตู้ 2 )m 3 x(m) 10 2 t (s) -5 x(m) 10 1
x 10 cos( t 3 )m 2
2
t (s)
17
例2. 由旋转矢量图（相量图） 画振动曲线、写振动方程。
已知:旋转矢量A=0.04m, =4(rad/s)
x
0.04
x(m)
/4
o
-0.04
1 16
1 1 16 2
t (s)
18
例3. 由振动方程画振动曲线。 已知方程：x 0.02 cos( t )m 2 2
2.机械振动的研究: 运动学—位移,速度,加速度,周期,频率。 动力学—力,能量。
2
简谐振动
§1 简谐振动的动力学方程
1、简谐振动的特点
回复力 f kx 的振动。
O
x
又如：单摆、复摆； 交流电、电磁振动。
3
2、简谐振动的动力学方程
f kx
d 2x m 2 kx dt
d 2x k x0 2 dt m
2）振幅A和初相 取决于初始条件x0 , v0
已知 , x0 , v0 ，则A和可求：
x A cost v A sin t
t0
x0 A cos v0 A sin
A
x
2 0
2
2 v0
tg
v0 x0
7
结论： 一个谐振子(确定m,k)，只能 有一个固定的频率，但可以有无数的 A 和，即可做无数种振动。
k m
d 2x 2x 0 dt 2
a 2 x
令：
方程解：
固有圆频率
x A cost
4
以上4式都是判断谐振的依据。
3、证明几种常见谐振动 证明单摆的微小摆动是简谐振动； 写振动方程；求振动周期。
解：任意处 合力f= mg sin ≈ m g
相差？
x—位移—质点对于平衡位置的位移。 A—振幅—质点到平衡位置的最大位移。 1 2 φ—初相位—t=0时的位相。 T
相差——相位的差。可用于比较两个谐振动
之间在振动步调上的差异。 设有两个同频率的谐振动，表达式分别为：
x1 A1 cos(t 10 )
x2 A2 cos(t 20 )