中考数学总复习 第一轮 同步演练 第三部分 统计与概率 第8章 概率与统计 第29节 数据的分析与

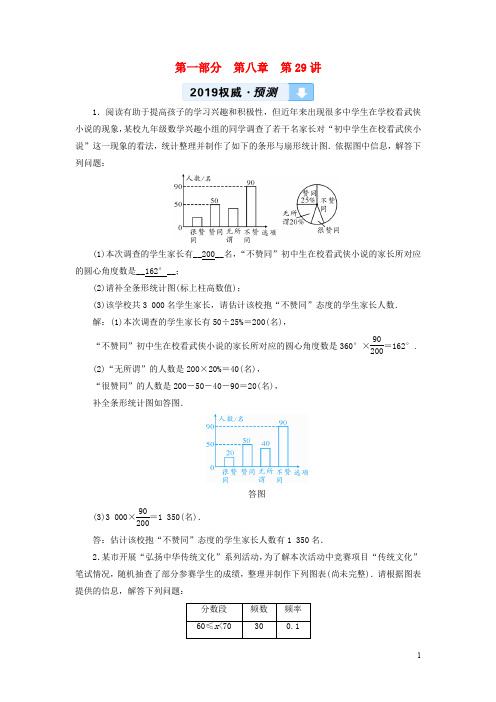
第一部分 第八章 第29讲1．阅读有助于提高孩子的学习兴趣和积极性，但近年来出现很多中学生在学校看武侠小说的现象，某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生在校看武侠小说”这一现象的看法，统计整理并制作了如下的条形与扇形统计图．依据图中信息，解答下列问题：(1)本次调查的学生家长有__200__名，“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是__162°__；(2)请补全条形统计图(标上柱高数值)；(3)该学校共3 000名学生家长，请估计该校抱“不赞同”态度的学生家长人数． 解：(1)本次调查的学生家长有50÷25%＝200(名)，“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是360°×90200＝162°.(2)“无所谓”的人数是200×20%＝40(名)， “很赞同”的人数是200－50－40－90＝20(名)， 补全条形统计图如答图．答图(3)3 000×90200＝1 350(名)．答：估计该校抱“不赞同”态度的学生家长人数有1 350名．2．某市开展“弘扬中华传统文化”系列活动，为了解本次活动中竞赛项目“传统文化”笔试情况，随机抽查了部分参赛学生的成绩，整理并制作下列图表(尚未完整)．请根据图表提供的信息，解答下列问题：(1)__300____120__n ＝__0.3__； (2)补全频数分布直方图；(3)若小聪同学的比赛成绩恰好是所有抽查学生成绩的中位数，则小聪同学的成绩落在__80≤x ＜90__分数段内；(4)如果比赛成绩80分以上(含80分)为优秀，那么该竞赛项目的优秀率是多少？ 解：(1)本次调查的样本容量为30÷0.1＝300， 则m ＝300×0.4＝120，n ＝90÷300＝0.3. (2)补全频数分布直方图如答图．答图(3)∵共有300个数据，其中位数是第150,151个数据的平均数，而第150,151个数据均落在80≤x <90分数段内，∴中位数在80≤x <90分数段内，即小聪同学的成绩落在80≤x <90分数段内． (4)该竞赛项目的优秀率是120＋60300×100%＝60%，答：该竞赛项目的优秀率是60%.。

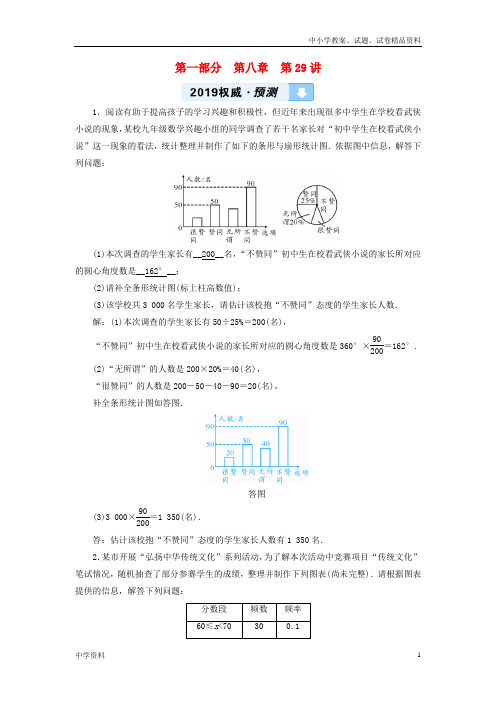
第一部分 第八章 第29讲1．阅读有助于提高孩子的学习兴趣和积极性，但近年来出现很多中学生在学校看武侠小说的现象，某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生在校看武侠小说”这一现象的看法，统计整理并制作了如下的条形与扇形统计图．依据图中信息，解答下列问题：(1)本次调查的学生家长有__200__名，“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是__162°__；(2)请补全条形统计图(标上柱高数值)；(3)该学校共3 000名学生家长，请估计该校抱“不赞同”态度的学生家长人数． 解：(1)本次调查的学生家长有50÷25%＝200(名)，“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是360°×90200＝162°.(2)“无所谓”的人数是200×20%＝40(名)， “很赞同”的人数是200－50－40－90＝20(名)， 补全条形统计图如答图．答图(3)3 000×90200＝1 350(名)．答：估计该校抱“不赞同”态度的学生家长人数有1 350名．2．某市开展“弘扬中华传统文化”系列活动，为了解本次活动中竞赛项目“传统文化”笔试情况，随机抽查了部分参赛学生的成绩，整理并制作下列图表(尚未完整)．请根据图表提供的信息，解答下列问题：(1)__300____120__n ＝__0.3__； (2)补全频数分布直方图；(3)若小聪同学的比赛成绩恰好是所有抽查学生成绩的中位数，则小聪同学的成绩落在__80≤x ＜90__分数段内；(4)如果比赛成绩80分以上(含80分)为优秀，那么该竞赛项目的优秀率是多少？ 解：(1)本次调查的样本容量为30÷0.1＝300， 则m ＝300×0.4＝120，n ＝90÷300＝0.3. (2)补全频数分布直方图如答图．答图(3)∵共有300个数据，其中位数是第150,151个数据的平均数，而第150,151个数据均落在80≤x <90分数段内，∴中位数在80≤x <90分数段内，即小聪同学的成绩落在80≤x <90分数段内． (4)该竞赛项目的优秀率是120＋60300×100%＝60%，答：该竞赛项目的优秀率是60%.。

1第一部分 第八章 课时291．已知一组数据：x,8,2,9,3的平均数为5，则这组数据的中位数和众数分别是( D )A ．4,3B ．4,4C ．3,4D ．3,3 【解析】根据平均数的计算，得x ＋8＋2＋9＋35＝5，解得x ＝3, ∵3出现次数最多，∴众数为3，把该组数按照从小到大的顺序排列：2,3,3,8,9，可得中位数为3.2．现有相同个数的A ，B ，C 三组数据，经过数据分析：数据的平均数x －甲＝x －乙＝x －丙，且s 2甲＝0.32，s 2乙＝0.28，s 2丙＝0.15，比较这三组数据的稳定性，下列说法正确的是( C )A ．甲比较稳定B ．乙比较稳定C ．丙比较稳定D ．无法确定 【解析】∵三组数据平均成绩相等，甲组的方差为0.32、乙组的方差为0.28、丙组的方差为0.15，∴丙组数据比较稳定．3．若一组数据x ，y ，z 的平均数为3，方差为2，那么数据3x,3y,3z 的平均数和方差分别是( A )A ．9,18B ．9,9C ．12,9D ．9,12 【解析】∵数据x ，y ，z 的平均数为3，∴13(x ＋y ＋z )＝3， ∴13(3x ＋3y ＋3z )＝3×13(x ＋y ＋z )＝3×3＝9. ∵数据x ，y ，z 的方差为2，∴13[(x －3)2＋(y －3)2＋(z －3)2]＝2， ∴3x,3y,3z 的方差为13[(3x －9)2＋(3y －9)2＋(3z －9)2]＝13[9(x －3)2＋9(y －3)2＋9(z －3)2]＝9×13[(x －3)2＋(y －3)2＋(z －3)2]＝9×2＝18.。

第一部分第八章课时29命题点一平均数、众数、中位数1．(2017·遵义)我市某连续7天的最高气温为28°，27°，30°，33°，30°，30°，32°，这组数据的平均数和众数分别是( D )A．28°，30°B．30°，28°C．31°，30°D．30°，30°【解析】数据28°，27°，30°，33°，30°，30°，32°的平均数是(28°＋27°＋30°＋33°＋30°＋30°＋32°)÷7＝30°，这组数据中30°出现了3次，出现的次数最多，则众数是30°.2．(2016·遵义)已知一组数据：60,30,40,50,70，这组数据的平均数和中位数分别是( C )A．60,50 B．50,60C．50,50 D．60,60【解析】这组数据的平均数是(60＋30＋40＋50＋70)÷5＝50；把这组数据从小到大排列为30,40,50,60,70，最中间的数是50，则中位数是50.3．(2014·遵义)有一组数据7,11,12,7,7,8,11.下列说法错误的是( A )A．中位数是7 B．平均数是9C．众数是7 D．极差是5【解析】这组数据按照从小到大的顺序排列为7,7,7,8,11,11,12，则中位数为8，平均数为7＋7＋7＋8＋11＋11＋127＝9，众数为7，极差为12－7＝5.故选A．命题点二方差及其意义4．(2018·遵义)贵州省第十届运动会将于2018年8月8日在遵义市奥体中心开幕，某校有2名射击队员在比赛中的平均成绩均为9环，如果教练要从中选1名成绩稳定的队员参加比赛，那么还应考虑这2名队员选拔成绩的( A )A．方差B．中位数C．众数D．最高环数【解析】如果教练要从中选1名成绩稳定的队员参加比赛，那么应考虑这2名队员选拔成绩的方差，方差越小，成绩越稳定．5．(2015·遵义)如果一组数据x1，x2，…，x n的方差是4，则另一组数据x1＋3，x2＋3，…，x n＋3的方差是( A )A．4 B．7C．8 D．19【解析】根据题意，设数据x1，x2，…，x n的平均数为a，则数据x1＋3，x2＋3，…，x n＋3的平均数为a＋3, 根据方差公式得s2＝1n{[(x1＋3)－(a＋3)]2＋[(x2＋3)－(a＋3)]2＋…＋[(x n＋3)－(a＋3)]2}＝1n[(x1－a)2＋(x2－a)2＋…＋(x n－a)2]＝4.。

第一部分 第八章 课时291．已知一组数据：x,8,2,9,3的平均数为5，则这组数据的中位数和众数分别是( D )A ．4,3B ．4,4C ．3,4D ．3,3 【解析】根据平均数的计算，得x ＋8＋2＋9＋35＝5，解得x ＝3, ∵3出现次数最多，∴众数为3，把该组数按照从小到大的顺序排列：2,3,3,8,9，可得中位数为3.2．现有相同个数的A ，B ，C 三组数据，经过数据分析：数据的平均数x －甲＝x －乙＝x －丙，且s 2甲＝0.32，s 2乙＝0.28，s 2丙＝0.15，比较这三组数据的稳定性，下列说法正确的是( C )A ．甲比较稳定B ．乙比较稳定C ．丙比较稳定D ．无法确定 【解析】∵三组数据平均成绩相等，甲组的方差为0.32、乙组的方差为0.28、丙组的方差为0.15，∴丙组数据比较稳定．3．若一组数据x ，y ，z 的平均数为3，方差为2，那么数据3x,3y,3z 的平均数和方差分别是( A )A ．9,18B ．9,9C ．12,9D ．9,12 【解析】∵数据x ，y ，z 的平均数为3，∴13(x ＋y ＋z )＝3， ∴13(3x ＋3y ＋3z )＝3×13(x ＋y ＋z )＝3×3＝9. ∵数据x ，y ，z 的方差为2，∴13[(x －3)2＋(y －3)2＋(z －3)2]＝2， ∴3x,3y,3z 的方差为13[(3x －9)2＋(3y －9)2＋(3z －9)2]＝13[9(x －3)2＋9(y －3)2＋9(z －3)2]＝9×13[(x －3)2＋(y －3)2＋(z －3)2]＝9×2＝18.。

第一部分 第八章 课时29命题点一 平均数、众数、中位数1．(2017·遵义)我市某连续7天的最高气温为28°，27°，30°，33°，30°，30°，32°，这组数据的平均数和众数分别是( D )A ．28°，30°B ．30°，28°C ．31°，30°D ．30°，30°【解析】数据28°，27°，30°，33°，30°，30°，32°的平均数是(28°＋27°＋30°＋33°＋30°＋30°＋32°)÷7＝30°，这组数据中30°出现了3次，出现的次数最多，则众数是30°.2．(2016·遵义)已知一组数据：60,30,40,50,70，这组数据的平均数和中位数分别是( C )A ．60,50B ．50,60C ．50,50D ．60,60【解析】这组数据的平均数是(60＋30＋40＋50＋70)÷5＝50；把这组数据从小到大排列为30,40,50,60,70，最中间的数是50，则中位数是50.3．(2014·遵义)有一组数据7,11,12,7,7,8,11.下列说法错误的是( A ) A ．中位数是7 B ．平均数是9 C ．众数是7D ．极差是5【解析】这组数据按照从小到大的顺序排列为7,7,7,8,11,11,12，则中位数为8，平均数为7＋7＋7＋8＋11＋11＋127＝9，众数为7，极差为12－7＝5.故选A ．命题点二 方差及其意义4．(2018·遵义)贵州省第十届运动会将于2018年8月8日在遵义市奥体中心开幕，某校有2名射击队员在比赛中的平均成绩均为9环，如果教练要从中选1名成绩稳定的队员参加比赛，那么还应考虑这2名队员选拔成绩的( A )A ．方差B ．中位数C ．众数D ．最高环数【解析】如果教练要从中选1名成绩稳定的队员参加比赛，那么应考虑这2名队员选拔成绩的方差，方差越小，成绩越稳定．5．(2015·遵义)如果一组数据x 1，x 2，…，x n 的方差是4，则另一组数据x 1＋3，x 2＋3，…，x n ＋3的方差是( A )A ．4B ．7C ．8D ．19【解析】根据题意，设数据x 1，x 2，…，x n 的平均数为a ，则数据x 1＋3，x 2＋3，…，x n ＋3的平均数为a ＋3, 根据方差公式得s 2＝1n{[(x 1＋3)－(a ＋3)]2＋[(x 2＋3)－(a ＋3)]2＋…＋[(x n ＋3)－(a ＋3)]2}＝1n[(x 1－a )2＋(x 2－a )2＋…＋(x n －a )2]＝4.。

》》》》》》》》》积一时之跬步 臻千里之遥程《《《《《《《《《《《《马明风整理第一部分 第八章 课时291．已知一组数据：x,8,2,9,3的平均数为5，则这组数据的中位数和众数分别是( D )A ．4,3B ．4,4C ．3,4D ．3,3 【解析】根据平均数的计算，得x ＋8＋2＋9＋35＝5，解得x ＝3, ∵3出现次数最多，∴众数为3，把该组数按照从小到大的顺序排列：2,3,3,8,9，可得中位数为3.2．现有相同个数的A ，B ，C 三组数据，经过数据分析：数据的平均数x －甲＝x －乙＝x －丙，且s 2甲＝0.32，s 2乙＝0.28，s 2丙＝0.15，比较这三组数据的稳定性，下列说法正确的是( C )A ．甲比较稳定B ．乙比较稳定C ．丙比较稳定D ．无法确定 【解析】∵三组数据平均成绩相等，甲组的方差为0.32、乙组的方差为0.28、丙组的方差为0.15，∴丙组数据比较稳定．3．若一组数据x ，y ，z 的平均数为3，方差为2，那么数据3x,3y,3z 的平均数和方差分别是( A )A ．9,18B ．9,9C ．12,9D ．9,12 【解析】∵数据x ，y ，z 的平均数为3，∴13(x ＋y ＋z )＝3， ∴13(3x ＋3y ＋3z )＝3×13(x ＋y ＋z )＝3×3＝9. ∵数据x ，y ，z 的方差为2，∴13[(x －3)2＋(y －3)2＋(z －3)2]＝2， ∴3x,3y,3z 的方差为13[(3x －9)2＋(3y －9)2＋(3z －9)2]＝13[9(x －3)2＋9(y －3)2＋9(z －3)2]＝9×13[(x －3)2＋(y －3)2＋(z －3)2]＝9×2＝18.。