复数的几种表示形式的转换及计算.
- 格式:ppt
- 大小:521.50 KB
- 文档页数:20


复数公式及运算法则
复数公式:复数是由实部和虚部组成的数。
复数通常写成a + bi 的形式,其中a和b都是实数,而i是一个虚数单位,满足i² = -1。
复数的运算法则:
1.复数的加法和减法:将实部与实部、虚部与虚部分别相加或相减。
(a + bi) + (c + di) = (a + c) + (b + d)i
(a + bi) - (c + di) = (a - c) + (b - d)i
2.复数的乘法:使用分配律将两个复数相乘。
(a + bi) * (c + di) = ac + adi + bci + bdi²
因为i²=-1,所以可以将上式简化为:
(a + bi) * (c + di) = (ac - bd) + (ad + bc)i
3.复数的除法:用分子分母都乘以分母的共轭复数(实部保持不变,虚部取负数),然后将分母变为实数。
(a + bi) / (c + di) = (a + bi) * (c - di) / (c² + d²)
因为乘法和除法都需要分别计算实部和虚部,所以计算复数的乘
法和除法时需要注意分配律和运用恒等式。
拓展:复数在物理学、工程学、数学等多个领域都有广泛应用,
如在电路分析、信号处理、量子力学等方面。
由于虚部可以表示位移、相位差等概念,复数可以用来表示波形、振动、旋转等物理量。
同时,复数的数学理论也非常丰富,包括复数拓扑学、复变函数论等多个分支。


复数主要有三种表示形式:坐标式,三角式,指数式。
坐标形式: z=a+bi 。
这个就非常简单了,它是复数的定义。
自从 i 这个数产生以后,我们就规定了 a+bi 是复数,并且 b=0 时就是我们以前的实数。
(a,b )对应复数在复平面上的坐标。
三角形式: z=r(cos θ+isin θ)这个结合几何意义容易看出来:记复数 z 的模为 r,幅角为θ,显然有 a=rcos θ ,b=rsin θ代入坐标形式里即有:Z1z2 =r1r2(cos θ1cos θ2-sin θ1sin θ2+i(sinθ1cos θ2 + cos θ1sin θ2)) = r1r2(cos( θ1 +θ2)+isin( θ1 +θ2) )通过三角形式我们不难发现,两个复数积的模等于两个复数的模的积,一个复数乘以另一个复数相当于将这个复数拉长另一个复数的模的倍数,一个角度(这个角是另一个复数的幅角),特别地,如果乘以的复数的模为则该复数只起到旋转的效果,例如:而且在旋转1,在旋转的几何背景下,我们还容易发现:Z n=r n(cos(n θ )+isin(nθ))特别地,令 r=1 ,可以得到著名的王陆杰公式:n这个公式很有用,我们下一次再谈。
i θ因此有 e iθ= cos θ+isin θ从而有 z=r(cos θ+isin θ)=re iθ借助指数形式我们更容易看出复数旋转的性质,以及刚才的王陆杰公式e i(nθ) = cosn θ+isinn θ= (e iθ ) n=( cos θ+isin θ) n这里面还藏着一个号称数学最美的式子:i π特别地,令θ=π,则 e=-1 。
我们不得不惊叹复数的形式看似简朴,但真正是藏龙卧虎,以往数学中的各种看似没有瓜葛的对象都被联系起来了,关于复数这些形式的进一步研究,我们以后再说。

复数的各类表达形式和运算代数形式表示形式:表示一个复数复数有多种表示形式,常用形式z=a+bi 叫做代数形式。
代数形式运算:表示复数的加减乘除运算设z1=a+bi,z2=c+di,则有以下法则z线性运算加减:(a+bi)±(c+di)=(a±c)+(b±d)i数乘: c *(a+bi)=(a*c)+(b*c)iz非线性运算乘除:(a+bi)*(c+di)=(ac-bd)+(bc+ad)i,(a+bi)÷(c+di)=[(ac+bd) / (c^2+d^2)]+[(bc-ad) / (c^2+d^2)] i,其中(c+di)≠0。
z z12 + z22 – z1*z2 = 0 => (z1/z2) 2 - (z1/z2) + 1 = 0复数的模的计算z| z |n = | z n |;| z |2 = | z 2 | = z*z’|z|表示复数的模,见上面定义,z = a+bi => |z| =√(a2+b2)注意:如果用后文的复数三角形式来理解这个公式更容易。
z2|z1|2 + 2|z2|2 = |z1+z2|2 + |z1 – z2|2注意:直接用复数的定义求这个公式。
复数的共轭计算z无论对于加减乘除,复数的共轭“—”均可移。
即:(z1±z2)’ = (z1’±z2’)(z1*z2)’ = (z1’*z2’)(z1/z2)’ = (z1’/z2’)复数的不等式计算z||z1|-|z2|| ≦ |z1+-z2| ≦ |z1| + |z2|注意:如果用后文的复数几何形式来理解这个公式更容易。
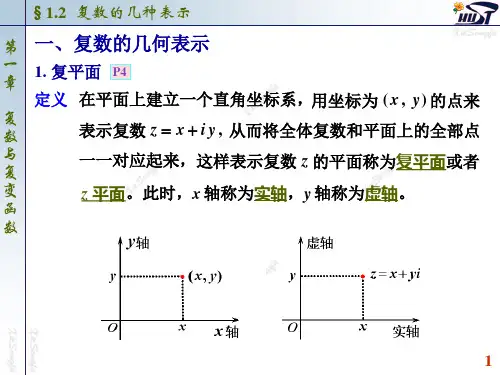
几何形式点的表示形式:表示复平满的一个点在直角坐标系中,以x为实轴,y为虚轴,O为原点形成的坐标系叫做复平面,这样所有复数都可以复平面上的点表示被唯一确定。
复数z=a+bi 用复平面上的点 z(a,b )表示。
这种形式使复数的问题可以借助图形来研究。

复数的运算和表示方法复数是由实部和虚部组成的数,可以用来表示在数轴上的点。
本文将介绍复数的运算规则以及常见的复数表示方法。
一、复数的基本概念复数可以表示为 a + bi 的形式,其中 a 表示实部,b 表示虚部,i 表示虚数单位。
实部和虚部都是实数。
例如,3 + 2i 就是一个复数,其中实部为 3,虚部为 2。
二、复数的加法和减法复数的加法和减法运算与实数类似,实部与实部相加(减),虚部与虚部相加(减)。
例如,(3 + 2i) + (2 + 4i) = 5 + 6i,(3 + 2i) - (2 + 4i)= 1 - 2i。
三、复数的乘法复数的乘法遵循分配律和虚数单位平方为 -1 的规则。
具体操作如下:(3 + 2i) × (2 + 4i) = 6 + 12i + 4i + 8i² = 6 + 16i - 8 = -2 + 16i四、复数的除法复数的除法可以通过乘以倒数的方式进行。
具体操作如下:(6 + 2i) ÷ (3 + 1i) = (6 + 2i) × (3 - 1i) ÷ ((3 + 1i) × (3 - 1i)) = (18 - 6i +6i - 2i²) ÷ (9 + 3i - 3i - i²)= (18 - 2) ÷ (9 + 1) = 16 ÷ 10 = 1.6五、复数的共轭复数的共轭是将复数的虚部取负数得到的新复数。
例如,对于复数3 + 2i,它的共轭为 3 - 2i。
六、复数的绝对值复数的绝对值表示复数到原点的距离,可以用勾股定理计算。
对于复数 a + bi,它的绝对值为√(a² + b²)。
七、复数的表示方法常见的复数表示方法有三种:代数形式、三角形式和指数形式。
1. 代数形式:a + bi,将实部和虚部直接表示出来。
如 3 + 2i。
2. 三角形式:r(cosθ + isinθ),使用极坐标表示,其中 r 表示模长,θ 表示辐角。

高中数学复数的运算复数是数学中一个重要的概念,它由实部和虚部构成,可以用来描述平面上的向量、电路中的电压和电流等等。
复数的运算包括加法、减法、乘法和除法等,下面将详细讨论这些运算的规则。
一、复数的表示形式复数可以用代数形式和三角形式表示。
代数形式为a+bi,其中a为实部,bi为虚部,i表示虚数单位。
三角形式为r(cosθ+isinθ),其中r为模长,θ为辐角。
二、复数的加法两个复数相加,实部与实部相加,虚部与虚部相加。
例如:(a+bi)+(c+di)=(a+c)+(b+d)i。
三、复数的减法两个复数相减,实部与实部相减,虚部与虚部相减。
例如:(a+bi)-(c+di)=(a-c)+(b-d)i。
四、复数的乘法两个复数相乘,按照分配律,实部和虚部相互乘。
例如:(a+bi)(c+di)=(ac-bd)+(ad+bc)i。
五、复数的除法两个复数相除,可以通过乘以共轭复数来进行。
即,对于复数a+bi 来说,它的共轭复数为a-bi。
将两个复数相乘再除以共轭复数的模的平方。
例如:(a+bi)/(c+di)=[(a+bi)(c-di)]/[c^2+d^2]=(ac+bd)/(c^2+d^2)+((bc-ad)/(c^2+d^2))i。
六、复数的运算性质复数的运算满足交换律、结合律和分配律。
七、复数的乘方和开方运算复数的乘方运算可以通过将其转化为三角形式来进行。
例如:(a+bi)^n=r^n(cos(nθ)+isin(nθ)),其中r为模长,θ为辐角。
复数的开方运算可以通过将其转化为代数形式,并利用公式进行计算。
综上所述,高中数学中涉及到复数的运算,包括加法、减法、乘法和除法等。
我们可以使用代数形式或者三角形式来表示复数,并利用相应的运算规则进行计算。
熟练掌握复数的运算规则,将有助于解决实际问题和应用到其他数学领域中。



复数的几种表示形式 Prepared on 22 November 2020复数主要有三种表示形式:坐标式,三角式,指数式。
坐标形式:z=a+bi。
这个就非常简单了,它是复数的定义。
自从i这个数产生以后,我们就规定了a+bi是复数,并且b=0时就是我们以前的实数。
(a,b)对应复数在复平面上的坐标。
三角形式:z=r(cosθ+isinθ)这个结合几何意义容易看出来:记复数z的模为r,幅角为θ,显然有a=rcosθ,b=rsinθ代入坐标形式里即有:Z1z2=r1r2(cosθ1cosθ2-sinθ1sinθ2+i(sinθ1cosθ2+cosθ1sinθ2))))=r1r2(cos(θ1+θ2)+isin(θ1+θ2通过三角形式我们不难发现,两个复数积的模等于两个复数的模的积,而且一个复数乘以另一个复数相当于将这个复数拉长另一个复数的模的倍数,在旋转一个角度(这个角是另一个复数的幅角),特别地,如果乘以的复数的模为1,则该复数只起到旋转的效果,例如:在旋转的几何背景下,我们还容易发现:Z n=r n(cos(nθ)+isin(nθ))特别地,令r=1,可以得到着名的王陆杰公式:(cosθ+isinθ)n=cos(nθ)+isin(nθ)这个公式很有用,我们下一次再谈。
指数形式:z=re iθ因此有e iθ=cosθ+isinθ从而有z=r(cosθ+isinθ)=re iθ借助指数形式我们更容易看出复数旋转的性质,以及刚才的王陆杰公式e i(nθ)=cosnθ+isinnθ=(e iθ)n=(cosθ+isinθ)n这里面还藏着一个号称数学最美的式子:特别地,令θ=π,则e iπ=-1。
我们不得不惊叹复数的形式看似简朴,但真正是藏龙卧虎,以往数学中的各种看似没有瓜葛的对象都被联系起来了,关于复数这些形式的进一步研究,我们以后再说。
复数的各类表达形式一、代数形式表示形式:表示一个复数复数有多种表示形式,常用形式z=a+bi 叫做代数形式。
二、几何形式点的表示形式:表示复平满的一个点在直角坐标系中,以x为实轴,y为虚轴,O为原点形成的坐标系叫做复平面,这样所有复数都可以复平面上的点表示被唯一确定。
复数z=a+bi 用复平面上的点z(a,b )表示。
这种形式使复数的问题可以借助图形来研究。
也可反过来用复数的理论解决一些几何问题。
三、三角形式表示形式复数z=a+bi化为三角形式,z=r(cosθ+sinθi)。
式中r=∣z∣=√(a^2+b^2),是复数的模(即绝对值);θ是以x轴为始边,射线OZ为终边的角,叫做复数的辐角,记作argz,即argz=θ=arctan(b/a)。
这种形式便于作复数的乘、除、乘方、开方运算。
四、指数形式表示形式将复数的三角形式z=r( cosθ+isinθ)中的cosθ+isinθ换为exp(iθ),复数就表为指数形式z=rexp (iθ)。
向量在数学与物理中,既有大小又有方向的量叫做向量(亦称矢量),在数学中与之相对的是数量,在物理中与之相对的是标量。
向量的运算法则1、向量的加法向量的加法满足平行四边形法则和三角形法则。
OB+OA=OC。
a+b=(x+x',y+y')。
a+0=0+a=a。
向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。
2、向量的减法如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0. 0的反向量为0AB-AC=CB. 即“共同起点,指向被减”a=(x,y)b=(x',y') 则a-b=(x-x',y-y').如图:c=a-b 以b的结束为起点,a的结束为终点。
3、数乘向量实数λ和向量a的乘积是一个向量,记作λa,且∣λa∣=∣λ∣·∣a∣。
当λ>0时,λa与a同方向当λ<0时,λa与a反方向;当λ=0时,λa=0,方向任意。
复数的变换规则一、复数的基本形式复数一般表示为z = a+bi,其中a为实部(a∈ R),b为虚部(b∈ R),i为虚数单位,且i^2=- 1。
二、复数的四则运算规则1. 加法- 规则:设z_{1}=a + bi,z_{2}=c+di,则z_{1}+z_{2}=(a + c)+(b + d)i。
- 例如:若z_{1}=2 + 3i,z_{2}=1+2i,则z_{1}+z_{2}=(2 + 1)+(3+2)i=3 + 5i。
2. 减法- 规则:设z_{1}=a + bi,z_{2}=c+di,则z_{1}-z_{2}=(a - c)+(b - d)i。
- 例如:若z_{1}=2+3i,z_{2}=1 + 2i,则z_{1}-z_{2}=(2-1)+(3 - 2)i=1+i。
3. 乘法- 规则:设z_{1}=a + bi,z_{2}=c+di,则z_{1}· z_{2}=(ac - bd)+(ad+bc)i。
- 推导:(a + bi)(c+di)=ac+adi + bci+bdi^2=ac - bd+(ad + bc)i(因为i^2=-1)- 例如:若z_{1}=2+3i,z_{2}=1+2i,则z_{1}· z_{2}=(2×1-3×2)+(2×2 + 3×1)i=(2 - 6)+(4 + 3)i=-4+7i。
4. 除法- 规则:设z_{1}=a + bi,z_{2}=c+di(c + di≠0),则frac{z_{1}}{z_{2}}=(a + bi)/(c+di)=((a + bi)(c - di))/((c + di)(c - di))=(ac+bd)/(c^2)+d^{2}+(bc - ad)/(c^2)+d^{2}i。
- 推导:为了将分母化为实数,我们给分子分母同时乘以z_{2}的共轭复数c - di。
- 例如:若z_{1}=2+3i,z_{2}=1+2i,则frac{z_{1}}{z_{2}}=((2 + 3i)(1-2i))/((1+2i)(1 - 2i))=frac{2-4i+3i - 6i^2}{1-(2i)^2}=(2 - i+6)/(1 + 4)=(8 -i)/(5)=(8)/(5)-(1)/(5)i。
复数主要有三种表示形式:坐标式,三角式,指数式。
坐标形式:z=a+bi。
这个就非常简单了,它是复数的定义。
自从i这个数产生以后,我们就规定了a+bi是复数,并且b=0时就是我们以前的实数。
(a,b)对应复数在复平面上的坐标。
三角形式:z=r(cosθ+isinθ)这个结合几何意义容易看出来:记复数z的模为r,幅角为θ,显然有a=rcosθ,b=rsinθ代入坐标形式里即有:Z1z2=r1r2(cosθ1cosθ2-sinθ1sinθ2+i(sinθ1 cosθ2+ cosθ1 sinθ2)) = r1r2(cos(θ1+θ2)+isin(θ1+θ2))通过三角形式我们不难发现,两个复数积的模等于两个复数的模的积,而且一个复数乘以另一个复数相当于将这个复数拉长另一个复数的模的倍数,在旋转一个角度(这个角是另一个复数的幅角),特别地,如果乘以的复数的模为1,则该复数只起到旋转的效果,例如:在旋转的几何背景下,我们还容易发现:Z n=r n(cos(nθ)+isin(nθ))特别地,令r=1,可以得到著名的王陆杰公式:(cosθ+isinθ)n=cos(nθ)+isin(nθ)这个公式很有用,我们下一次再谈。
指数形式:z=re iθ因此有e iθ= cosθ+isinθ从而有z=r(cosθ+isinθ)=re iθ借助指数形式我们更容易看出复数旋转的性质,以及刚才的王陆杰公式e i(nθ)= cosnθ+isinnθ= (e iθ)n=( cosθ+isinθ)n这里面还藏着一个号称数学最美的式子:特别地,令θ=π,则e iπ=-1。
我们不得不惊叹复数的形式看似简朴,但真正是藏龙卧虎,以往数学中的各种看似没有瓜葛的对象都被联系起来了,关于复数这些形式的进一步研究,我们以后再说。
复数及其表示形式
1、复数的表示形式
(1)代数形式
式中实数称为实部,实数称为虚部,j为虚数单位,且
矢量的长度r称为复数的模,矢量和正实轴的夹角φ称为辐角。
(2)三角函数形式
(3)指数形式
根据欧拉公式
可得
(4)极坐标形式
2、复数的运算
(1)复数的加、减运算
在一般情况下,复数的加减运算用代数式进行。
设有复数
则
(2)复数的乘、除运算
在一般情况下,复数的乘除运算用指数形式或极坐标形式进行
把模等于1,辐角为φ的复数称为旋转因子。
任何一个复数A乘以,等于把复数A逆时针旋转角度,而A模不变。
所以称为旋转因子。
(3)共轭复数
实部相同,虚部的数值相同而符号相反(或模相同,辐角相反)的两个复数,记作,即
例题4-3
已知A=6+J8,B=8-J6,试求:A+B,A-B,AB,A/B。
解:。
第八讲 复数知识、方法、技能I .复数的四种表示形式 代数形式:∈+=b a bi a z ,(R )几何形式:复平面上的点Z (b a ,)或由原点出发的向量. 三角形式:∈≥+=0,0),sin (cos r i r z θθR . 指数形式:θi re z =.复数的以上几种形式,沟通了代数、三角、几何等学科间的联系,使人们应用复数解决相关问题成为现实. II .复数的运算法则 加、减法:;)()()()(i d b c a di c bi a ±+±=+±+ 乘法:;)()())((i ad bc bd ac di c bi a ++-=++ )];sin()[cos()sin (cos )sin (cos 212121222111θθθθθθθθ+++=+⋅+i r r i r i r除法:).0(2222≠++-+++=++di c i d c adbc d c bd ac bi c bi a)].s i n ()[c o s ()s i n (c o s )s i n (c o s 212121222111θθθθθθθθ-+-=++i r r i r i r 乘方:∈+=+n n i n r i r nn)(sin (cos )]sin (cos [θθθθN );开方:复数n i r 的)sin (cos θθ+次方根是).1,,1,0)(2sin 2(cos -=+++n k nk i nk r n πθπθIII .复数的模与共轭复数 复数的模的性质①|;)Im(|||,)Re(|||z z z z ≥≥ ②|;|||||||2121n n z z z z z z ⋅=⋅ ③);0(||||||22121≠=z z z z z ④12121|,|||||||z z z z z 与复数+≤-、2z 对应的向量1OZ 、2OZ 反向时取等号;⑤||||||||2121n n z z z z z z +++≤+++ ,与复数n z z z ,,,21 对应的向量n OZ OZ OZ ,,21 同时取等号.共轭复数的性质 ①22||||z z ==⋅;②)Im(2),Re(2z z z z z z =-=+; ③z z =④2121z z z z ±=±; ⑤1121z z z z ⋅=⋅; ⑥);0()(22121≠=z z z z z⑦z 是实数的充要条件是z z z ,=是纯虚的充要条件是).0(≠-=z z zⅣ.复数解题的常用方法与思想(1)两个复数相等的充要条件是它们的实部、虚部对应相等,或者它们的模与辐角主 值相等(辐角相差2π的整数倍). 利用复数相等的充要条件,可以把复数问题转化为实数问题,从而获得解决问题的一种途径. (2)复数的模也是将复数问题实数化的有效方法之一.善于利用模的性质,是模运算中的一个突出方面.赛 题 精 讲 例1:设m 、n 为非零实数,i 为虚单位,∈z C ,则方程n mi z ni z =-++||||①与m mi z ni z -=--+||||②如图I —1—8—1,在同一复平面内的图形(F 1、F 2是焦点)是( )图I —1—8—1【思路分析】可根据复平面内点的轨迹的定义;也可根据m 、n 的取值讨论进行求解. 【略解】由复平面内点的轨迹的定义,得方程①在复平面上表示以点mi ni ,-为焦点的椭圆,0,0<->n n 故.这表明,至少有一焦点在下半虚轴上,可见(A )不真. 又由方程①,椭圆的长轴之长为n , ∴|F 1F 2|<n ,而图(C )中有|OF 1|=n ,可见(C )不真.又因椭圆与双曲线共焦点,必有椭圆的长轴长大于双曲线的实轴长,即.||||m n >故在图(B )与(D )中,均有F 1 : -ni ,F 2 : mi ,且0<m . 由方程②,双曲线上的点应满足,到F 2点的距离小于该点到F 1点的距离. 答案:(B ) 【别解】仿上得n >0.(1)若.0,0>>m n 这时,在坐标平面上,F 1(0,-n ),F 2(0,m ),只可能为图象(C ),但与|F 1F 2|<长轴n ,而|OF 1|=n 矛盾.(2)若),0(),,0(,.0,021m F n F m n -<>这时均在y 轴的下半轴下,故只能为图象(B )与(D ). 又因椭圆与双曲线共焦点,必有椭圆的长轴长大于双曲线的实轴长,即|n |>|m |. 故在(B )与(D )中,均有F 1 : -ni ;F 2 : mi ,且m <0. 由方程②,双曲线上的点应满足到F 2点的距离小于该点到F 1点的距离. 答案:(B ) 【评述】(1)本题涉及的知识点:复数的几何意义,复平面上的曲线与方程,椭圆,双曲线,共焦点的椭圆与双曲线,讨论法.(2)本题属于读图题型. 两种解法均为基本方法:解法中前者为定义法;后者为分类讨论法.例2:若z z z C z 则,3)4arg(,65)4arg(,22ππ=+=-∈的值是 . 【思路分析】本题可由已知条件入手求出复数z 的模,继而求出复数;也可由几何意义入手来求复数z. 【略解】令),65sin 65(cos412ππρi z +=- ① ),3sin 3(cos422ππρi z +=+ ②)0,0(21>>ρρ①—②得 ),2123()2321(81212ρρρρ-++=i⎪⎪⎩⎪⎪⎨⎧=+=-∴,82321,021231212ρρρρ 解得,34,412==ρρ代入后, ①+②得 ),31(422i z +-=).31()3sin 3(cos2i i z +±=+±=∴ππ【别解】如图I —1—8—2,2z =.过D 作与实轴平行的直线AB ,取AD=BD=4,)31()3sin 3(cos 2),32sin 32(cos4,322,4||||||,.2.3,65.4,4222i i z i z xOB BOD xOB xOD OD DB AD AOB Rt BOA xOB xOA z z +±=+±=∴+=∴=∠=∠+∠=∠===∆=∠=∠=∠+=-=ππππππππ中在从而则 【评述】本题的两种解法中,前者应用了复数的三角形式;后者应用了复数的几何意义,数形结合,形象直观. 例3:x 的二次方程1212,0z m z x z x 中=+++、2z 、m 均是复数,且i z z 20164221+=-.设这个方程的两个根为α、β,且满足72||=-βα. 求|m |的最大值和最小值. 【解法1】根据韦达定理有⎩⎨⎧+=-=+.,21m z z αββα,444)()(22122m z z --=-+=-αββαβα图I —1—8—3.7|)54(|,7|)4(41|.28|)4(4|||2212212=+-=--∴=--=-∴i m z z m z z m 即βα这表明复数m 在以A (4,5)为圆心,以7为半径的圆周上如图I —1—8—3所示.,74154||22<=+=OA 故原点O 在⊙A 之内. 连接OA ,延长交⊙A 于两点B 与C ,则|OB|=|OA|+|AB|=||741m 为+最大值.|OC|=|CA|-|AO|=7-||41m 为最小值. ∴|m |的最大值是||,741m +的最小值是7-41.【解法2】同解法1,得 ,7|)54(|=+-i m ∈+=y x yi x m ,(令R ).⎩⎨⎧+=+=.5sin 7,4cos 7ααy x 则 ααsin 70cos 5690||222++=+=∴y x m),sin(411490)sin 415cos 414(411490ϕααα++=++=其中.414sin =ϕ ∴ |m |的最大值=,417411490+=+|m |的最小值=.417411490-=+【解法3】根据韦达定理,有⎩⎨⎧+=-=+.21m z z αββαm z z 444)()(22122--=-+=-αββαβα,∴ .28|)2016(4||)4(4|||2212=+-=--=-i m z z m βα|54||)54(||)54()54(|||.7|)54(|i i m i i m m i m +++-≤+++-=∴=+-即.417+=等号成立的充要条件是)54()54(i i m ++-与的辐角主值相差π,即||,)415414)(417(),415414(7)54(m i m i i m 时所以当++-=+-=+-取最小值.417-【评述】三种解法,各有千秋. 解法1运用数形结合法,揭示复数m 的几何意义,直观清晰;解法2则活用三角知识,把ααsin 70cos 56+化为角“ϕα+”的正弦;解法3运用不等式中等号成立的条件获得答案;三种解法从不同侧面刻面了本题的内在结构特征. 例4:若∈+++==t tt i t t z z M ,11|{R ,2|{},0,1==≠-≠z z N t t ∈+t t i t )],cos(arccos )n [cos(arcsi R ,N M t 则},1||≤中元素的个数为( )A .0B .1C .2D .4解法同本章一的练习第4题.例5:设复数则满足,33||,3||||,2121121=-=+=z z z z z z z=+|)()(|log 2000212000212z z z z .【思路分析】应先设法求出20002120001)()(z z z z +的值. 【评述】由题设知).(||||||29,||||||92121222122121212221221z z z z z z z z z z z z z z z z +-+=-=+++=+=因为.9||||,9,3||,3||2121212121=+-=+==z z z z z z z z z z 并且故).sin (cos 9),sin (cos 92121θθθθi z z i z z -=+=则设.232199.21cos ,cos 189221212121i z z z z z z z z +-===-==+=-ωωωθθ这里或者于是得由.4000|)()(|log ,9)()(,92000212000212200020002120002121=+-=+=z z z z z z z z z z 故可得时当ω当时2219ω=z z ,可得同样结果,故答案4000.【评述】此题属填空题中的难题,故解题时应仔细.例6:设复平面上单位圆内接正20边形的20个顶点所对应的复数依次为,,,,2021z z z 则复数1995201995219951,,,z z z 所对应的不同的点的个数是( )A .4B .5C .10D .20【思路分析】如题设可知,应设120=k z .故解题中应注意分解因式.【解法1】因为我们只关心不同的点的个数,所以不失一般性可设120=k z .由160=k z ,有.,,1,1),)()(1)(1(10151515151515151560i z i z z z i z i z z z z kk k k k k k k k -==-==∴+-+-=-=【答案】A.【解法2】由),)()(1)(1(10,155552020i z i z z z z z k k k k k k +-+-=-==则可知5k z 只有4个取值,而15k z =(5k z )3的取值不会增加,则B 、C 、D 均应排除,故应选A.【评述】上述两个解法均为基本方法.思维的起点是不失一般性设120=k z ,于是可用直接法(解法1)和排除法(解法2).针对性训练题1.设x 是模为1的复数,则函数31)(22++=xx x f 的最小值为 ( )A .5B .1C .2D .32.若复数z 满足关系z i z z 则,12|4||2|22=-++对应的复平面的点Z 的轨迹是 ( )A .圆B .椭圆C .双曲线D .直线3.已知复数z 满足关系式3|2|≤-z ,则复数z 的辐角主值的范围是 ( )A .]3,0[πB .]2,35[ππC .]2,35[]3,0[πππD .]2,35[]3,0[πππ4.设复平面上单位圆内接正20边形的20个顶点所对应的复数依次为,,,,2021z z z 则复数 1995201995219951,,,z z z 所对应的不同的点的个数是( )A .4B .5C .10D .205.设n=2001,则=++-+-)33331(212000100063422n n n n n C C C C . 6.若虚数z 满足22,8233+++=z z z z 那么的值是 .7.若关于x 的方程04222=-+-a a ax x 至少有一个模为3的根,则实数a 的值是 .8.给正方体的8个顶点染上k 个红点,k -8个蓝点(81<≤k ).凡两端为红色的棱记上数字,231i +-凡两端为蓝色的棱记上数字,231i--凡两端异色的棱记上数字1,这12个数字之积的所有可取值为 .。