南师附中物理竞赛讲义-12.1欧姆定律

《探究欧姆定律》讲义一、什么是欧姆定律在电学的世界里，欧姆定律就像是一把万能钥匙，能够帮助我们打开理解电路中电流、电压和电阻关系的大门。

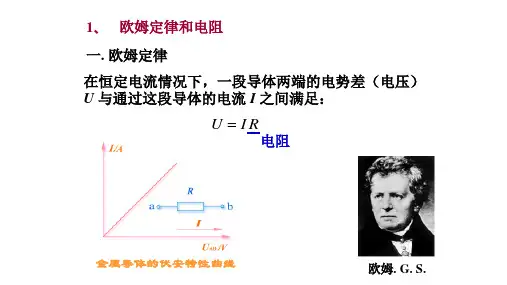
欧姆定律指出：通过一段导体的电流与这段导体两端的电压成正比，与这段导体的电阻成反比。

用数学公式来表达，就是 I ＝ U ／ R，其中 I 表示电流，单位是安培（A）；U 表示电压，单位是伏特（V）；R 表示电阻，单位是欧姆（Ω）。

二、欧姆定律的发现历程欧姆定律的发现并非一蹴而就，而是经历了一番艰辛的探索。

德国物理学家乔治·西蒙·欧姆在 19 世纪初期进行了大量的实验研究。

当时的实验条件相当简陋，但欧姆凭借着坚韧不拔的毅力和对科学的执着追求，不断改进实验方法和设备。

他尝试了各种不同的材料和电路连接方式，经过无数次的测量和分析，最终得出了电流、电压和电阻之间的定量关系，也就是我们现在所熟知的欧姆定律。

欧姆的发现为电学的发展奠定了坚实的基础，也让我们更加深刻地认识到自然界中物理规律的美妙和神奇。

三、欧姆定律的实验验证为了更好地理解和验证欧姆定律，我们可以通过简单的实验来进行。

实验器材包括电源、电阻器、电流表和电压表。

首先，将电源、电阻器、电流表串联在电路中，电压表并联在电阻器两端。

然后，改变电源的电压，同时记录下相应的电流和电压值。

通过对实验数据的分析，可以发现电流与电压的比值始终保持不变，这个比值就是电阻。

这就直观地验证了欧姆定律中电流与电压成正比的关系。

接下来，保持电源电压不变，更换不同阻值的电阻器，再次测量电流。

会发现电流随着电阻的增大而减小，验证了电流与电阻成反比的关系。

需要注意的是，在实验过程中，要确保实验仪器的准确性和实验操作的规范性，以减少误差。

四、欧姆定律的应用欧姆定律在我们的日常生活和工业生产中有着广泛的应用。

在家庭电路中，我们可以根据欧姆定律计算出电器的功率。

功率 P＝ U × I，知道了电压和电流，就能算出电器消耗的电能。

12.1欧姆定律一、电阻的大小1、电阻的计算式（欧姆定律）U R I =2、电阻的决定式（电阻定律）l R Sρ= 微观解释：电阻产生的原因，是定向移动的自由电子与原子核碰撞。

长度越长，碰撞概率越大 横截面积越大，碰撞概率越小 3、电阻率与温度的关系：0(1)t ρρα=+微观解释：对于金属：温度高，分子热运动剧烈，碰撞概率大，电阻升高，α为正值 对于绝缘体：温度高，更多电子挣脱束缚，成为自由电子，电阻降低，α为负值二、网络电阻的化简1、利用电路的对称性进行折叠、翻转、合并拆分（1）设网络电阻的两端点为A 和B 。

AB 的这根对称轴两侧的对称是“完全对称”。

可以看成是两条支路并联，因此只需计算一条支路的电阻，并将总电阻除以2，相当于将原电路沿AB 折叠，电阻变粗，电阻值减半。

如果电阻就在对称轴上，相当于是中间一条支路上的电阻，则折叠过程中不受影响 （2）AB 中垂线的两侧具有不完全的对称性。

虽然电阻网络的分布是对称的，但是电路中电势的分布是不对称的，一边高一边低。

由这种不完全的对称性可以得到： <1>中垂线上各点电势相等①等电势的点之间，可以用导线任意连接②等势点间若存在电阻，则此支路上电流为0，可将此支路断开 <2>对称的支路上电流大小相等，因此可以将节点处的电路分离 2、利用电路的自相似性进行化简弄清究竟谁和谁自相似自相似性一般适用于半无限网络。

注意相似比的大小 3、等效电路在不改变电路性质的情况下，可以对电路进行变形、翻转，导线可以伸缩移动（节点移动不能跨过电路元件），三维图形可以“压扁”为二维图形。

4、电流注入法用均匀电阻线做成的正方形回路，如图，由九个相同的小正方形组成．小正方形每边的电阻均为r=8Ω．(1)在A 、B 两点问接入电池，电动势E=5.7V ，内阻不计，求流过电池的电流强度．(2)若用导线连接C 、D 两点，求通过此导线的电流(略去导线的电阻)．电阻丝无限网络如图所示，每一段金属丝的电阻均为r ，试求A 、B 两点间的等效电阻R AB ．由十二个相同的电阻连接成一个立方体框架，若每个电阻的阻值均为R 问从立方体八个顶点中的任意两个顶点测量时立方体的总电阻等于多少？1. 三个相同的金属圈两两相交地焊接成如图所示的形状，若每一金属圈的原长电阻（即它断开时测两端的电阻）为R ，试求图中A 、B 两点之间的电阻.【解析】从图看出，整个电阻网络相对A 、B 两点具有上、下对称性，因此可上、下压缩成如图所示的等效简化网络，其中r 为原金属圈长度部分的电阻，即有:r=R/4图网络中从A 点到O 点电流与从O 点到B 点的电流必相同；从A ′点到O 点的电流与从O 点到B ′点电流必相同.因此可将O 点断开，等效成图所示简化电路.B ′A ′AA继而再简化成如图所示的电路:最后可算得: R AB =1225512r r r -+=（） 即有R AB =5R/48.如图所示，无限旋转内接正方形金属丝网络由一种粗细一致、材料相同的金属丝构成，其中每个内接正方形的顶点都在外侧正方形四边中点上．已知与最外侧正方形边长相同的同种金属丝A'B'的电阻为R 0，求网络中：(1)A 、C 两端间等效电阻R AC ． (2)E 、G 两端间等效电阻R EG ．例1. 如图所示，框架是用同种金属丝制成的，单位长度的电阻为ρ，一连串内接等边三角形的数目可认为趋向无穷，取AB 边长为a ，以下每个三角形的边长依次减小一半，则框B ′BA ′AAB ′BA ′架上A 、B 两点间的电阻为多大？从对称性考虑原电路可以用如图所示的等效电路来代替，同时我们用电阻为2ABR 的电阻器来代替由无数层“格子”所构成的“内”三角，并且电阻是RAB 这样的，AB x R R =，R αρ=因此/2/2()()/2/2x x x x x RR RR R R R R R R R R R =+⋅++++解此方程得到：11)3AB x R R a ρ===如图所示是一个由电阻丝构成的平面正方形无穷网络，各小段的电阻为R ，求A 、B 两点间的等效电阻.若将A 、B 间的一小段电阻丝换成电阻为4R 的另一小段电阻丝.试问换后A 、B 间的等效电阻是多少?解析:设想内阻极大的电源加在A 和地(或无穷远)之间,使由A 点流进网络的电流为I ，则由对称性可知,流过AB 的电流为4I.假设拆去此电源,在B 点和地(或无究远)之间加上另一内AB B2/阻极大的电源,使由B 点流出网络的电流强度为I,由对称性可知,流过AB 的电流仍为4I.若把上述电源同时加上,则由叠加原理可知,流过AB 的电流为442I I I+=.设AB 间的等效电阻为R AB ，所以：2AB I IR R =⋅2AB R R =外的其它电阻丝构成的网络的电阻为R0，则整个电阻可以看成是除A 、B 间电阻丝与R0的并联.则:002AB R R RR R R ==+0R R =当A 、B 间的一小段电阻丝换成电阻为4R 时,则:004'0.84AB R RR R R R⋅==+.有一无限平面导体网络，它由大小相同的正六边形网眼组成，如图所示．所有六边形每边的电阻均为R 0． (1)求结点a 、b 间的电阻．(2)如果有电流I 由a 点流入网络，由g 点流出网络，那幺流过de 段电阻的电流I de 为多大?【解析】（1）设有电流I 自a 点流入，流到四面八方无穷远处，那么必有3/I 电流由a 流向c ，有6/I电流由c 流向b .再假设有电流I 由四面八方汇集b 点流出，那么必有6/I 电流由a 流向c ，有3/I电流由c 流向b .将以上两种情况综合，即有电流I 由a 点流入，自b 点流出，由电流叠加原理可知263II I I ac =+=（由a 流向c ） 263I I I I cb =+=（由c 流向b ）因此，a 、b 两点间等效电阻000R I R I R I I U R cb ac AB AB =+==（2）假如有电流I 从a 点流进网络，流向四面八方，根据对称性，可以设 A I I I I ===741B I I I I I I I ======986532应该有I I I A =+B 63因为b 、d 两点关于a 点对称，所以A be deI I I 21=='同理，假如有电流I 从四面八方汇集到g 点流出，应该有 BdeII =''最后，根据电流的叠加原理可知()I I I I I I I I B A B A de dede 61636121=+=+=''+'=如图，有一三角形的无穷长电路其中每个电阻阻值均为R ，求AB 间的等效电阻R AB 。

知识网络重难点聚焦1．欧姆定律公式中的三个物理量应是对同一部分电路而言；计算时单位一定要统一；会用欧姆定律的变形公式求电压和电阻。

2．根据欧姆定律分析电表的变化问题及分析电路的故障。

这既是本章的难点，也是中考热点。

此类型题分两种情况：①是电路里滑动变阻器滑片滑动时，会引起电路里一系列物理量的变化，不管变阻器是串联在电路里还是并联在电路里，当变阻器连入电路里的阻值变大时，电路里的总阻值都变大，总电流都变小，然后根据欧姆定律再进行分析；②开关闭合或断开时，关键是分析电路的构成。

3．根据欧姆定律求极值问题。

为了保护电流表，电流不能超过0.6A或3A量程;为了保护电压表,电压不能超过3V或15V,可按电流表和电压表的量程,求电阻的临界值,再根据欧姆定律求极值。

4.选择题中的定性判断和定量计算是电学的核心,是中考的重点和热点,题目中等难度或中等难度以上，要求时刻围绕欧姆定律以及串、并联电路中电流、电压、电阻的特点来进行,要熟记串联电阻的分压作用和并联电阻的分流作用。

5.安全用电的常识:熟记几种电压值;知道电压越高越危险;了解预防触电及触电救护知识;注意防雷。

一、电阻1.电阻（R）：表示导体对电流的阻碍作用导体如果对电流的阻碍作用越大，那么电阻就越大，而通过导体的电流就越小）。

国际单位：欧姆（Ω）；常用：兆欧（MΩ），千欧（KΩ）；1兆欧=103千欧；1千欧=103欧。

2.决定电阻大小的因素：材料，长度，横截面积，另外还与温度有关（R 与它的U 和I 无关）。

3.滑动变阻器：原理：改变电阻线在电路中的长度来改变电阻的。

作用：（1）通过改变接入电路中的电阻来改变电路中的电流和电压。

（2）防止电流过大烧坏用电器铭牌：如一个滑动变阻器标有“50Ω2A”表示的意义是：最大阻值是50Ω，允许通过的最大电流是2A.正确使用：a ，应串联在电路中使用；b ，接线要“一上一下”;c ，通电前应把阻值调至最大的地方。

1.有甲、乙、丙三根用同种材料制成的导线，已知甲和乙粗细相同，但甲比乙长；乙和丙的长度相同，但乙比丙细。

欧姆定律知识点3 伏安法测定电阻的阻值定值电阻的阻值一般固定不变，在额定电压下或实际电压低于额定电压时，定值电阻的温度变化很小，温度对定值电阻的影响很小，一般忽略不计。

[注意事项]（1）连接电路时，开关必须断开，电流表、电压表的接法要分别串联、并联，电流表与小灯泡串联，电压表与小灯泡并联。

还要注意电流表、电压表量程的选择以及正、负接线柱的接法。

滑动变阻器采用“一上一下”接法与小灯泡串联。

（2）接通电路前，移动滑动变阻器滑片，使变阻器接入电路中的电阻最大，使串联电路电流最小，保护电路元件。

（3）加在小灯泡两端的电压不要超过额定电压太多，否则会烧坏小灯泡。

（4）移动滑片P改变小灯泡两端电压时，要紧盯电压表示数，并留意电流表示数变化情况，不要盲目乱动，造成不必要的损坏。

知识点4 额定电压●额定电压：用电器正常工作时所需的电压，叫做额定电压。

如果实际电压比额定电压高很多，很可能损坏用电器；如果实际电压比额定电压低很多，用电器就不能正常工作，有时还会损坏用电器。

●额定电流：用电器在额定电压下流过的电流叫额定电流。

例如，若灯泡标有“3.8V 0.3A”字样，“3.8V”是该小灯泡的额定电压，“0.3A”是该小灯泡的额定电流。

一般每个用电器都标有额定电压和额定电流值，对用电器造成损坏的原因往往是电流过大，实际电流大于额定电流时，易损坏用电器，实际电流小于额定电流时，用电器不能正常工作，有时易损坏用电器。

四、欧姆定律和安全用电知识点1 电压越高越危险●触电是人体直接或间接与火线连通，有较大的电流通过人体造成的。

触电的起因是人体直接或间接与火线连通。

触电危险的真正原因是有较大的电流通过人体。

因为人体是导体，当人体触及带电体时，有电流通过人体，电流对人体的危险性跟电流大小、通电时间长短等因素有关，通过人体的电流为8~10mA，人手就很难摆脱带电体，通过人体的电流达到100mA，只要很短时间，就会使人窒息，心跳停止，即发生触电事故时，电流越大，从触电到死亡的时间越短。

《探究欧姆定律》讲义一、什么是欧姆定律在电学的世界里，欧姆定律就像是一座重要的桥梁，连接着电压、电流和电阻这三个关键要素。

简单来说，欧姆定律表明了通过一段导体的电流与这段导体两端的电压成正比，与这段导体的电阻成反比。

用数学公式来表达就是：I ＝ U ／ R 。

其中，I 代表电流，单位是安培（A）；U 代表电压，单位是伏特（V）；R 代表电阻，单位是欧姆（Ω）。

这个定律可不是凭空想象出来的，而是经过无数科学家的实验和研究总结出来的。

它对于我们理解和分析电路中的各种现象起着至关重要的作用。

二、欧姆定律的发现历程欧姆定律的发现并非一蹴而就，而是经历了一个漫长而曲折的过程。

乔治·西蒙·欧姆，这位德国物理学家，经过大量的实验和不懈的努力，终于在 1826 年发现了这一重要定律。

在当时，实验条件有限，测量工具也不够精确，但欧姆凭借着坚定的信念和严谨的科学态度，不断改进实验方法和装置。

他使用了不同的材料和长度的导线进行实验，通过测量电流、电压和电阻的值，经过反复的计算和分析，最终得出了电流与电压、电阻之间的关系。

欧姆的发现最初并没有得到广泛的认可和重视，甚至遭到了一些权威的质疑和批评。

但随着时间的推移，越来越多的实验验证了欧姆定律的正确性，它逐渐成为了电学领域的基本定律之一。

三、欧姆定律的实验验证为了更好地理解欧姆定律，让我们一起来进行一个简单的实验。

实验器材：电源、电阻箱、电流表、电压表、导线若干。

实验步骤：1、按照电路图连接好实验电路，确保连接牢固，无短路现象。

2、调节电阻箱的阻值，分别记录下不同阻值时电压表和电流表的示数。

3、根据测量的数据，计算出每次实验中的电流值和电阻值，验证是否满足 I ＝ U ／ R 。

通过实验，我们可以直观地看到，当电阻不变时，电压增大，电流也随之增大；当电压不变时，电阻增大，电流则减小。

这充分证明了欧姆定律的正确性。

四、欧姆定律在电路中的应用欧姆定律在实际电路中有着广泛的应用。

12.2含电源的欧姆定律一、含源电路的欧姆定律计算两点a 到b 的电势降落值U a -U b 。

即规定了走向为a 到b正负号规则：1、对于电阻等用电器，若电流方向与走向一致，电势降落值为正，反之为负。

2、对于电源，顺着走向，若是从正极到负极，电势降低，电势降落值为正，反之为负。

如图，电流向右，走向也向右：1122a b U U Ir IR Ir εε-=++-+若电流向右，走向向左，计算U b -U a1122b a U U Ir IR Ir εε-=---+-若电流向左，走向也向左：若电流向左，走向向右：二、基尔霍夫定律1、基尔霍夫第一定律（节点电流定律）对于任意一个节点，流入的总电流等于流出的总电流2、基尔霍夫第一定律（回路电压定律）对于任意一个回路，绕回路一周，电势降落的代数和为0思考：对于一个电路，一共要列多少方程？电流方程数等于节点数减1，电压方程数等于最简回路的个数例1、如图所示的电路中，E1=12V ，r 1=1Ω，E 2=8V ，r 2=O.5Ω，R 1=3Ω，R 2=1.5Ω，R 3=4Ω．试求通过每个电阻的电流．例2、在图所示的回路中，已知三节电池的电动势和内阻分别为E1=4V，E2=E3=2V，r1=r2=r3=1Ω，定值电阻R1=7Ω，R2=1Ω，R3=3Ω，求AB间的电压U AB．例3、如图所示，7个相同的电阻R构成一个二端网络．试求A、B两点之间的等效电阻R AB．二、△-Y 形变换例4、证明：在满足以下变换关系式时，以下两种电阻连接方式完全等效：(1)对应节点间的电压相等（两图中的U 12、U 23、U 31分别相等）(2)对应支路上的电流相等（两图中的I 1、I 2、I 3分别相等）特例：各电阻阻值相同 △变为 Y ，R =R 0/3Y 变为 △，R =3R 0例5、求右图电路中的干路电流例6、用△-Y 形变换解例3如图所示，7个相同的电阻R 构成一个二端网络．试求A 、B 两点之间的等效电阻R AB ．例7、电阻丝网络如图所示，每一小段电阻均为R ，求A 、B 之间的等效电阻R AB解法1：△-Y 变换解法2：注入电流法A B。