2-2 几种常见的力
- 格式:ppt
- 大小:1.79 MB
- 文档页数:18


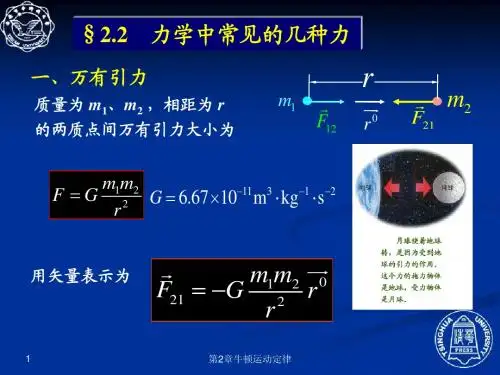
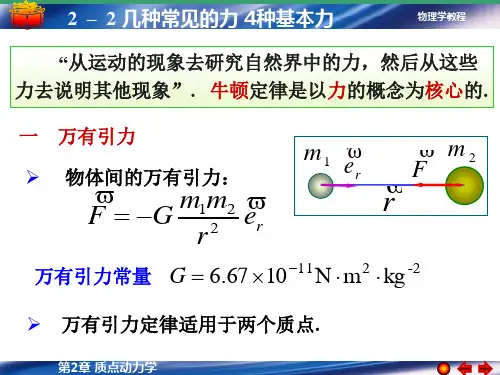
大学物理(2.2.2)--常见力非惯性系惯性力一、几种常见的力1.万有引力(Law of Gravitation )1)文字叙述:在两个相距为r ,质量分别为m 1,m 2的质点间有万有引力,其方向沿着它们的连线,其大小与它们的质量的乘积成正比,与它们之间的距离的平方成反比,即2)数学表示 0221r r m m G F = ——引力质量Gravitational Mass其中 211..1067.6--?=kg m N G ——引力常量。
2.重力(Gravity )——本质上归结于万有引力。
1)文字叙述:物体重力就是指忽略地球的自转效应时,地球表明附近物体所受的地球的引力,即物体与地球之间的万有引力。
其方向指向地心。
2)数学表示 G=mg g=9.8m.s -2——重力加速度。
3)思考题:赤道的重力加速度大还是两极的重力加速度大?为什么?3.弹性力(Elastic Force )大家知道,两个物体相互接触,彼此将产生形变,使其内部产生反抗力——形变恢复力(弹性力)。
形变是产生弹性力的条件之一。
例如:板擦和桌子相互接触,彼此有了一定的形变,在各自的接触部分产生弹性力。
所以,弹性力是一种与物体的形变有关的接触力。
即发生形变的物体,由于要恢复原状,对与它接触的物体会产生力的作用,这种物体因形变而产生欲使其恢复原来形状的力叫做弹性力。
常见的弹性力有:1)弹簧中的弹性力:弹簧被拉伸或压缩时产生的弹性力。
胡克定律(Hooke Law ):在弹性限度内,弹性力的大小与弹簧的伸长量成正比,方向指向平衡位置。
数学表示 f=-kx—— k 为弹簧的劲度系数(Stiffness )。
k 的值决定于弹簧本身的性质。
而弹簧弹性力的方向总是指向平衡位置。
2)绳子被拉紧时所产生的张力绳的张力:即绳内部各段之间的弹性作用力。
下面以AB 段为研究对象,设其质量为m A 点和B 点的张力:'A A T T -=、'B B T T -=由牛顿第二定律:a m T T B A =+(1)当a =0或者m →0时,F T T B A =-=',绳子上各点张力相同而且拉力相等。




力的种类
在物理学中,力是指导致物体产生运动或形变的物理量。
力的种类多种多样,
常见的力包括:
1.重力:地球或其他天体吸引物体的力,是最普遍的力之一。
重力使
物体朝着地球的中心运动,决定了物体在重力场中的运动轨迹。
2.弹力:当物体受到挤压或拉伸时,恢复原状的力就是弹力。
弹簧、
橡皮等材料都具有弹性,可以产生弹力。
3.摩擦力:当两个物体相对运动或相互接触时产生的阻碍运动的力。
摩擦力可以分为静摩擦力和动摩擦力,影响物体在表面上的滑动或滚动。
4.拉力:以拉拽形式作用在物体上的力。
例如绳索或链条拉扯物体时
施加的力就是拉力。
5.压力:在物体表面向内或外方向的力。
压力是单位面积上的力,可
以是气体或液体对物体施加的力。
6.电磁力:电荷之间相互作用的力称为电力,磁场中的磁性物质所受
的力称为磁力。
电磁力是一种非接触力,广泛存在于自然界中。
7.核力:原子核内部质子和中子之间的相互作用力,主要负责维持原
子核的结构稳定。
8.弯曲力:作用于梁、柱等结构上的力,使结构产生弯曲或变形的力。
以上列举的力只是物理学中常见的一部分,不同环境和情况下会有更多种类的
力作用在物体上,影响着物体的运动和形变。
通过深入了解各种力的性质和作用方式,可以更好地理解物体运动和结构力学的基本原理。



力的分类
命名:
1、性质:重力、弹力、摩擦力……
2、作用效果:拉力、压力、推力、支持力……
常见的力
最常见的一种力——重力:
⑴重力的概念:地面附近的物体,由于地球的吸引而受的力叫重力。
重力的施力物体是:地球。
⑵重力大小的计算公式G=mg 其中g=9.8N/kg 它表示质量为1kg 的物体所受的重力为
9.8N。
⑶重力的方向:竖直向下,其应用是重垂线、水平仪分别检查墙是否竖直和面是否水平。
⑷重力的作用点——重心:重力在物体上的作用点叫重心。
质地均匀外形规则物体的重心,在它的几何中心上。
如均匀细棒的重心在它的中点,球的重心在球心。
方形薄木板的重心在两条对角线的交点
摩擦力:
1、定义:两个互相接触的物体,当它们要发生或已发生相对运动时,就会在接触面上产生一种阻碍相对运动的力叫摩擦力。
条件:①接触;②挤压;③相对运动或相对运动的趋势
2、分类:
滑、滚动摩擦
3、摩擦力的方向:摩擦力的方向与物体相对运动的方向相反,有时起阻力作用,有时起动力作用。
5、应用:⑴增大摩擦力的方法有:增大压力、接触面变粗糙变滚动为滑动。
⑵减小摩擦的方法有三:减小压力接触面变光滑、变滑动为滚动(滚动轴承)使接触面彼此分开(加润滑油)。
摩擦力平衡求解,下节课说
静摩擦力大小应通过受力分析,结合二力平衡求得。