下载文档原格式
决策树习题练习（答案）决策树习题练习答案1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。
两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】（1）绘制决策树，见图1；100×10 -20×10 60×1020×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 3202 31 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。
（3）决策比较节点②与节点③的期望收益值可知，大规模投资方案优于小规模投资方案，故应选择大规模投资方案，用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。
A方案的投资额为500万元，其年净收益在产品销售好时为150万元，，销售差时为50万元；B方案的投资额为300万元，其年净收益在产品销路好时为100万元，销路差时为10万元，根据市场预测，在项目寿命期内，产品销路好时的可能性为70%,销路差的可能性为30％，试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】（1）首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。
（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元) 机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
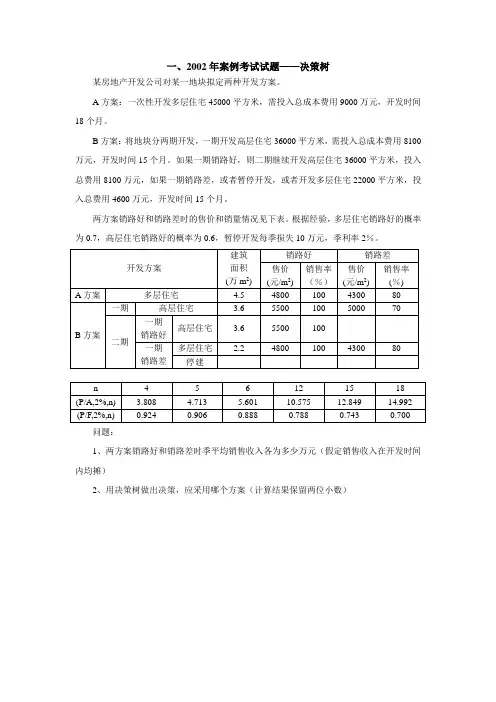
一、2002年案例考试试题——决策树某房地产开发公司对某一地块拟定两种开发方案。
A方案：一次性开发多层住宅45000平方米，需投入总成本费用9000万元，开发时间18个月。
B方案：将地块分两期开发，一期开发高层住宅36000平方米，需投入总成本费用8100万元，开发时间15个月。
如果一期销路好，则二期继续开发高层住宅36000平方米，投入总费用8100万元，如果一期销路差，或者暂停开发，或者开发多层住宅22000平方米，投入总费用4600万元，开发时间15个月。
两方案销路好和销路差时的售价和销量情况见下表。
根据经验，多层住宅销路好的概率为0.7，高层住宅销路好的概率为0.6，暂停开发每季损失10万元，季利率2％。
问题：1、两方案销路好和销路差时季平均销售收入各为多少万元（假定销售收入在开发时间内均摊）2、用决策树做出决策，应采用哪个方案（计算结果保留两位小数）答案：1、A方案开发多层住宅：销路好4.5×4800×100％÷6＝3600（万元）销路差4.5×4300×80％÷6＝2580（万元）B方案一期开发高层住宅：销路好3.6×5500×100％÷5＝3960（万元）销路差3.6×5000×70％÷5＝2520（万元）B方案二期开发高层住宅：3.6×5500×100％÷5＝3960（万元）开发多层住宅：销路好2.2×4800×100％÷5＝2112（万元）销路差2.2×4300×80％÷5＝1513.6（万元）2、机会点①净现值的期望值：(3600×0.7＋2580×0.3)×(P/A,2％,6)－9000=(3600×0.7＋2580×0.3)×5.601－9000=9449.69（万元）等额年金：9449.69×(A/P,2％,6)=9449.69×1/5.601=1687.14（万元）机会点③净现值的期望值：3960×(P/A，2％，5)×1.0－8100=3960×4.713×1.0－8100=10563.48（万元）等额年金：10563.48×(A/P,2％,5)=10563.48×1/4.713=2241.35（万元）机会点④净现值的期望值：－10×(P/A,2％,5)=－10×4.713=－47.13（万元）等额年金：－47.13×(A/P,2％,5)=－47.13×1/4.713=－10.00（万元）机会点⑤净现值的期望值：(2112×0.7＋1513.6×0.3)×(P/A,2％,5)－4600=(2112×0.7＋1513.6×0.3)×4.713－4600=4507.78（万元）等额年金：4507.78×(A/P,2％,5)=4507.78×1/4.713=956.46（万元）根据计算结果判断，B方案在一期开发高层住宅销路差的情况下，二期应改为开发多层住宅。
决策树习题练习（答案）决策树习题练习答案1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。
两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】（1）绘制决策树，见图1；100×10 -20×10 60×1020×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 3202 31 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。
（3）决策比较节点②与节点③的期望收益值可知，大规模投资方案优于小规模投资方案，故应选择大规模投资方案，用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。
A方案的投资额为500万元，其年净收益在产品销售好时为150万元，，销售差时为50万元；B方案的投资额为300万元，其年净收益在产品销路好时为100万元，销路差时为10万元，根据市场预测，在项目寿命期内，产品销路好时的可能性为70%,销路差的可能性为30％，试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】（1）首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。
（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元) 机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
决策树习题练习(答案)决策树题练答案题目1：某投资者预计投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。
两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15.试用决策树法选择最优方案。
解答：首先绘制决策树，如图1所示。
然后计算各状态点的期望收益值，并将其标在圆圈上方。
最后比较节点②与节点③的期望收益值，选择期望收益值更高的方案，即大规模投资方案。
题目2：某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。
A方案的投资额为500万元，其年净收益在产品销售好时为150万元，在销售差时为50万元；B方案的投资额为300万元，其年净收益在产品销路好时为100万元，在销路差时为10万元。
根据市场预测，在项目寿命期内，产品销路好时的可能性为70%，销路差的可能性为30％，试根据以上资料对方案进行比选。
已知标准折现率ic10%。
解答：首先画出决策树，如图2所示。
然后计算各个机会点的期望值，最后计算各个备选方案净现值的期望值，选择期望净现值更高的方案，即方案A。
根据计算，方案A的净现值期望值为33万元，方案B的净现值期望值为148.5万元。
因此，选择方案B为优先方案。
接着，投资者提出了第三个方案，先进行小规模投资160万元，生产3年后根据销售情况再决定是否进行大规模投资。
根据表2的销售概率表，绘制出决策树，计算各节点的期望收益值。
经过计算，节点④的期望收益值为616万元，节点⑤的期望收益值为-140万元，节点②的期望收益值为281.20万元，节点⑧的期望收益值为476万元，节点⑨的期望收益值为392万元，因此选择扩建方案。
节点⑥的期望损益值取扩建方案的期望损益值476万元。
节点⑦的期望收益值为140万元。
某建筑公司计划建一预制构件厂，方案一为建大厂，需投资300万元，每年可盈利100万元，若销路差则每年亏损20万元，使用期为10年；方案二为建小厂，需投资170万元，每年可盈利40万元，若销路差则每年盈利30万元。
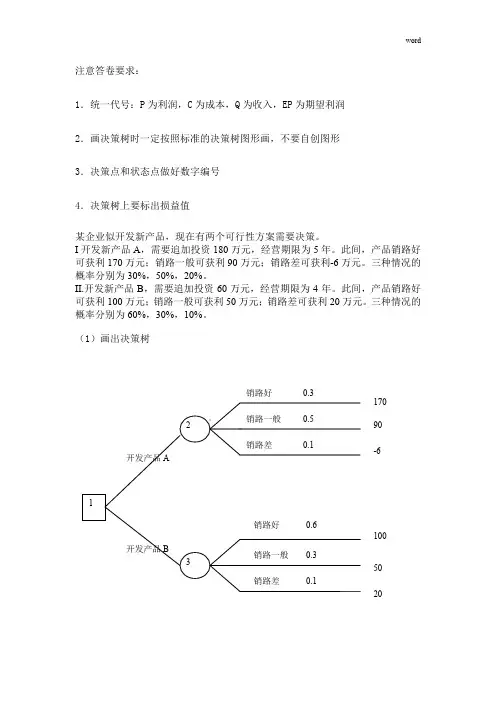
注意答卷要求：1．统一代号：P 为利润，C 为成本，Q 为收入，EP 为期望利润 2．画决策树时一定按照标准的决策树图形画，不要自创图形 3．决策点和状态点做好数字编号 4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。
I 开发新产品A ，需要追加投资180万元，经营期限为5年。
此间，产品销路好可获利170万元；销路一般可获利90万元；销路差可获利-6万元。
三种情况的概率分别为30%，50%，20%。
II.开发新产品B ，需要追加投资60万元，经营期限为4年。
此间，产品销路好可获利100万元；销路一般可获利50万元；销路差可获利20万元。
三种情况的概率分别为60%，30%，10%。
（1）画出决策树销路好 0.317090 -61005020（2）计算各点的期望值，并做出最优决策求出各方案的期望值：方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值：方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。
某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（1）公司组织技术人员逐渐改进技术，使用期是10年；（2）购买先进技术，这样前期投入相对较大，使用期是10年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。
预计该种产品前四年畅销的概率为0.7，滞销的概率为0.3。
如果前四年畅销，后六年畅销的概率为0.9；若前四年滞销，后六年滞销的概率为0.1。
相关的收益数据如表所示。
（1）画出决策树（2）计算各点的期望值，并做出最优决策投资收益表单位：万元解（1）画出决策树，R为总决策，R1为二级决策。
决策树习题练习（答案）决策树习题练习答案1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。
两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】（1）绘制决策树，见图1；100×10 -20×10 60×1020×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 3202 31 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。
（3）决策比较节点②与节点③的期望收益值可知，大规模投资方案优于小规模投资方案，故应选择大规模投资方案，用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。
A方案的投资额为500万元，其年净收益在产品销售好时为150万元，，销售差时为50万元；B方案的投资额为300万元，其年净收益在产品销路好时为100万元，销路差时为10万元，根据市场预测，在项目寿命期内，产品销路好时的可能性为70%,销路差的可能性为30％，试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】（1）首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。
（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元) 机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
