决策树的例题

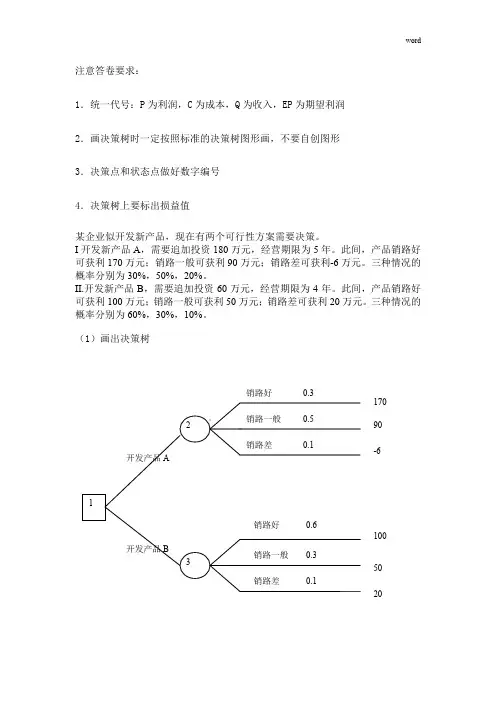
注意答卷要求：1．统一代号：P 为利润，C 为成本，Q 为收入，EP 为期望利润 2．画决策树时一定按照标准的决策树图形画，不要自创图形 3．决策点和状态点做好数字编号 4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。

I 开发新产品A ，需要追加投资180万元，经营期限为5年。

此间，产品销路好可获利170万元；销路一般可获利90万元；销路差可获利-6万元。

三种情况的概率分别为30%，50%，20%。

II.开发新产品B ，需要追加投资60万元，经营期限为4年。

此间，产品销路好可获利100万元；销路一般可获利50万元；销路差可获利20万元。

三种情况的概率分别为60%，30%，10%。

（1）画出决策树销路好 0.317090 -61005020（2）计算各点的期望值，并做出最优决策求出各方案的期望值：方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值：方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。

某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（1）公司组织技术人员逐渐改进技术，使用期是10年；（2）购买先进技术，这样前期投入相对较大，使用期是10年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。

预计该种产品前四年畅销的概率为0.7，滞销的概率为0.3。

如果前四年畅销，后六年畅销的概率为0.9；若前四年滞销，后六年滞销的概率为0.1。

相关的收益数据如表所示。

（1）画出决策树（2）计算各点的期望值，并做出最优决策投资收益表单位：万元解（1）画出决策树，R为总决策，R1为二级决策。

人工智能决策树例题经典案例一、经典案例：天气预测决策树在天气预测中有广泛应用，下面是一个关于是否适宜进行户外运动的示例：1. 数据收集：- 温度：高（>30℃）/中（20℃-30℃）/低（<20℃）- 降水：是/否- 风力：高/中/低- 天气状况：晴朗/多云/阴天/雨/暴雨- 应该户外运动：是/否2. 构建决策树：- 根据温度将数据分为三个分支：高温、中温、低温- 在每个分支中，继续根据降水、风力和天气状况进行划分，最终得到是否适宜户外运动的决策3. 决策树示例：温度/ / \高温中温低温/ | | \ |降水无降水风力适宜/ \ | | / \是否高中低| |不适宜适宜- 如果温度是高温且有降水，则不适宜户外运动- 如果温度是高温且无降水，则根据风力判断，如果风力是高，则不适宜户外运动，如果风力是中或低，则适宜户外运动 - 如果温度是中温，则不论降水和风力如何，都适宜户外运动- 如果温度是低温，则需要考虑风力，如果风力是高，则适宜户外运动，如果风力是中或低，则不适宜户外运动4. 参考内容：决策树的构建和应用：决策树通过对输入特征进行划分，构建了一棵树形结构，用于解决分类或回归问题。

构建决策树主要包括数据预处理、特征选择、划分策略和停止条件等步骤。

特征选择可以使用信息增益、基尼指数等算法，划分策略可以使用二叉划分或多叉划分，停止条件可以是叶子节点纯度达到一定阈值或达到预定的树深度。

决策树的应用包括数据分类、特征选择和预测等任务。

天气预测案例中的决策树：将天气预测问题转化为分类问题，通过构建决策树，可以得到识别是否适宜户外运动的规则。

决策树的决策路径可以用流程图或树状图表示，帮助理解和解释决策过程。

决策树的节点表示特征值，分支表示判断条件，叶子节点表示分类结果。

决策树的生成算法可以基于启发式规则或数学模型，如ID3、C4.5、CART等。

决策树的优缺点：决策树具有可解释性强、易于理解和实现、能处理非线性关系等优点。

决策树习题练习（答案）决策树习题练习答案1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。

两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。

试用决策树法选择最优方案。

表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】（1）绘制决策树，见图1；100×10 -20×10 60×1020×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 3202 31 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。

（3）决策比较节点②与节点③的期望收益值可知，大规模投资方案优于小规模投资方案，故应选择大规模投资方案，用符号“//”在决策树上“剪去”被淘汰的方案。

2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。

A方案的投资额为500万元，其年净收益在产品销售好时为150万元，，销售差时为50万元；B方案的投资额为300万元，其年净收益在产品销路好时为100万元，销路差时为10万元，根据市场预测，在项目寿命期内，产品销路好时的可能性为70%,销路差的可能性为30％，试根据以上资料对方案进行比选。

已知标准折现率ic=10%。

【解】（1）首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。

（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元) 机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。

决策树实例计算计算题⼀ 1.为⽣产甲产品，⼩⾏星公司设计了两个基本⽅案：⼀是建⼤⼯⼚，⼆是建⼩⼯⼚。

如果销路好，3年以后考虑扩建。

建⼤⼯⼚需投资300万元，建⼩⼯⼚需投资160万元，3年后扩建另需投资140万元。

扩建后可使⽤7年，其年度损益值与⼤⼯⼚相同。

每种⾃然状态的预测概率及年度损益值如下表：前 3 年后 7 年根据上述资料试⽤决策树法做出决策。

四、计算题（15分）答：建⼤⼚收益=581-300=281建⼩⼚收益=447-160=287所以应选择建⼩⼚⽅案。

⼆⼭姆公司的⽣产设备已经落后，需要马上更新。

公司有⼈认为，⽬前产品销路增长，应在更新设备的同时扩⼤再⽣产的规模。

但也有⼈认为，市场形势尚难判断，不如先更新设备，3年后再根据形势变化考虑扩⼤再⽣产的规模问题。

这样，该公司就⾯临着两个决策⽅案。

决策分析的有关资料如下：A、现在更新设备，需投资35万元， 3年后扩⼤⽣产规模，另需投资40万元。

B、现在更新设备的同时扩⼤再⽣产的规模，需投资60万元。

C、现在只更新设备，在销售情况良好时，每年可获利6万元；在销售情况不好时，每年可获利4、5万元。

D、如果现在更新与扩产同时进⾏，若销售情况好，前3年每年可获利12万元；后7年每年可获利15万元；若销售情况不好，每年只获利3万元。

E、每种⾃然状态的预测概率如下表前 3 年后 7 年根据上述资料试⽤决策树法做出决策。

答案：结点7收益值=0、85×7 × 15+0、15 ×7 ×3=92、4（万元）结点8收益值=0、85×7 ×6+0、15 ×7 ×4、5=40、4（万元）结点9收益值=0、1×7 × 15+0、9 ×7 ×3=29、4（万元）结点10收益值=0、1×7 × 6+0、9 ×7 ×4、5=32、6（万元）结点1收益值=0、7×[52、4+（3 × 6）]+0、3 ×[32、6+（3 × 4、5）]=63、1（万元）结点2收益值=0、7×[92、4+（3 × 12）]+0、3 ×[29、4+（3 × 3）]=101、4（万元）答：⽤决策树法进⾏决策应选择更新扩产⽅案，可获得收益41、4万元。

决策树算法例题经典
案例1：购物产品推荐。

假设当前我们需要进行购物产品推荐工作，用户可以选择若干项属性，例如品牌、价格、颜色、是否有折扣等等，在已知一些样本的基础上，构
建一棵决策树，帮助用户快速得到最佳购买推荐。

如果用户选择的品牌为A，则直接推荐产品P3；如果选择品牌为B，
则继续考虑价格，如果价格低于100，则推荐产品P1，否则推荐产品P2。

如果用户选择的品牌为C，则直接推荐产品P4。

当然，这只是一个简单的例子，实际应用场景中可能会有更多的属性
和样本。

因此，在构建决策树时需要考虑选取最优特征，避免过度拟合等
问题。

案例2：疾病预测。

假设有一组医学数据，其中包括患者的年龄、性别、身高、体重、血
压等指标以及是否患有糖尿病的标签信息。

我们希望构建一个决策树来帮
助医生快速判断患者是否可能患有糖尿病。

如果患者年龄大于45岁，则进一步考虑体重，如果体重高于120kg，则判断为高风险群体；否则判断为低风险群体。

如果患者年龄不超过45岁，则直接判断为低风险群体。

当然，这只是一个简单的例子，实际应用场景中可能会有更多的指标
和样本。

因此，在构建决策树时需要考虑选取最优特征，避免过度拟合等
问题。

《决策树习题练习（答案）》摘要：20×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 320 2 3 1 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方，100 10 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -300 2 3 1 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18，点⑦：150×0.3+100×0.5+50×0.2＝105（万元）点②：105×0.3-3×0.7＝29.4（万元）点⑧：110×0.2+60×0.7+0×0.1＝64（万元）点⑨：110×0.4+70×0.5+30×0.1＝82（万元）点④：82×0.4-2×0.6＝31.6（万元）点⑩：70×0.2+30×0.5-10×0.3＝26（万元）点⑤：26×0.7-2×0.3＝17.6（万元）点⑥：0 （3）选择最优方案决策树习题练习答案 1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。

两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。

试用决策树法选择最优方案。

表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7 100 60 销路差 0.3 -20 20 【解】（1）绘制决策树，见图1；100×10 -20×10 60×10 20×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 320 2 3 1 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。

以下是一个决策树经典例题的简单介绍：
例题：假设某工厂要生产一种新产品，根据市场调研，该产品有三种可能的销售情况：高、一般、低。

工厂有三种生产方案：大、中、小。

1. 方案一为大生产方案，预计在高销售情况下获得100万元利润，一般销售情况下获得40万元利润，低销售情况下获得20万元利润。

2. 方案二为中生产方案，预计在高销售情况下获得80万元利润，一般销售情况下获得50万元利润，低销售情况下获得30万元利润。

3. 方案三为小生产方案，预计在高销售情况下获得60万元利润，一般销售情况下获得45万元利润，低销售情况下获得50万元利润。

根据这些信息，我们需要使用决策树方法来选择最优的生产方案。

首先，我们需要确定问题的目标，这里的目标是最优利润。

然后，我们需要确定决策树的结构，包括树的根节点（工厂的生产方案）和每个分支（每种生产方案的预期利润）。

接着，我们需要计算每个分支的期望值（每种生产方案的预期利润乘以每种销售情况发生的概率），并根据期望值选择最优的分支作为决策树的下一级节点。

最后，我们重复上述步骤，直到找到最优的生产方案。

通过计算，我们可以得出大生产方案的期望值为72.73万元、中生产方案的期望值为64.67万元和小生产方案的期望值为58.67万元。

因此，根据决策树方法的选择规则，我们应该选择大生产方案作为最优的生产方案。

希望对您有所帮助！。

人工智能决策树例题决策树是人工智能和机器学习中用于分类和回归问题的一种常用算法。

可以通过对训练数据集的学习，构建出一棵决策树，用于对新数据进行分类。

下面是一个基于人工智能的决策树算法的例子：假设我们有一个银行客户数据集，其中包含以下特征：年龄、收入、婚姻状况、信用评分等。

我们的目标是预测客户是否会流失（即停止使用该银行的服务）。

首先，我们使用决策树算法对训练数据集进行学习，构建出一棵决策树。

这棵决策树会对每个节点进行判断，将数据分成不同的群组，并对每个群组进行分类。

例如，一个节点可能判断“年龄小于30”的客户更容易流失，而另一个节点可能判断“信用评分高于700”的客户不容易流失。

然后，我们可以使用这棵决策树来预测新客户的流失风险。

对于每个新客户，我们可以根据他们的特征信息，沿着决策树的路径进行判断，最终得到他们的流失风险。

需要注意的是，决策树算法虽然简单易懂，但也可能存在过度拟合的问题。

为了避免这个问题，我们通常会对决策树进行剪枝操作，或者使用集成学习等技术来提高模型的泛化能力。

下面是一个关于决策树的经典例题：例题描述：假设我们有一个数据集，包含不同年龄段的人群（年轻、中年、老年）以及他们的收入水平（低、中、高）、是否拥有房产（是/否）等信息，并且我们要根据这些特征预测一个人是否会购买某种理财产品。

构建决策树步骤：1. 选择一个最优属性作为根节点。

通常通过计算信息增益、信息增益率或基尼不纯度来确定，例如首先以“收入水平”作为划分标准。

2. 对于“收入水平”，我们可以创建三个分支：-收入低的分支，可能大多数人未购买理财产品；-收入中的分支，进一步基于其他特征如年龄、是否有房进行判断；-收入高的分支，可能多数人购买了理财产品。

3. 在每个子集中，继续寻找最优属性并分割数据，直到达到预定条件（如所有样本属于同一类别或者达到预设的最大深度）。

最终形成的决策树模型会像一棵树形结构，从根节点开始，每个内部节点表示一个属性测试，每个分支代表该属性的一个输出值，而每个叶节点则对应一种预测结果（是否购买理财产品）。

1.为生产甲产品，小行星公司设计了两个基本方案：一是建大工厂，二是建小工厂。

如果销路好，3年以后考虑扩建。

建大工厂需投资300万元，建小工厂需投资160万元，3年后扩建另需投资140万元。

扩建后可使用7年，其年度损益值及大工厂相同。

每种自然状态预测概率及年度损益值如下表：前 3 年后 7 年根据上述资料试用决策树法做出决策。

2山姆公司生产设备已经落后，需要马上更新。

公司有人认为，目前产品销路增长，应在更新设备同时扩大再生产规模。

但也有人认为，市场形势尚难判断，不如先更新设备，3年后再根据形势变化考虑扩大再生产规模问题。

这样，该公司就面临着两个决策方案。

决策分析有关资料如下：A、现在更新设备，需投资35万元， 3年后扩大生产规模，另需投资40万元。

B、现在更新设备同时扩大再生产规模，需投资60万元。

C、现在只更新设备，在销售情况良好时，每年可获利6万元；在销售情况不好时，每年可获利4、5万元。

D、如果现在更新及扩产同时进行，若销售情况好，前3年每年可获利12万元；后7年每年可获利15万元；若销售情况不好，每年只获利3万元。

E、每种自然状态预测概率如下表前 3 年后 7 年根据上述资料试用决策树法做出决策。

3某公司为满足某地区对某一产品需求设计了三个方案：第一个方案是新建一个大工厂,需投资320万元；第二个方案是新建一个小工厂,需投资140万元；第三方案是先投资140万元建造一个小工厂,三年以后,如果销路好再考虑扩建，扩建需追加投资200万元,收益及新建大工厂方案相同。

根据预测该产品在前三年销路好概率为0.7，销路差概率为0.3。

如果前三年销路好,后七年销路好概率为0.9,销路差概率为0.1;如果前三年铺路差,则后七年销路必定差。

每个方案收益如下表所示。

4华美莱公司准备生产甲种新产品，对未来3年市场预测资料如下：企业现在有两个方案可以选择：（1）新建一个新产品生产车间，投资需140万元；（2）扩建原有车间，投资需60万元。