河南省郑州枫杨外国语中学2017-2018学年八年级上期期中考试数学试卷

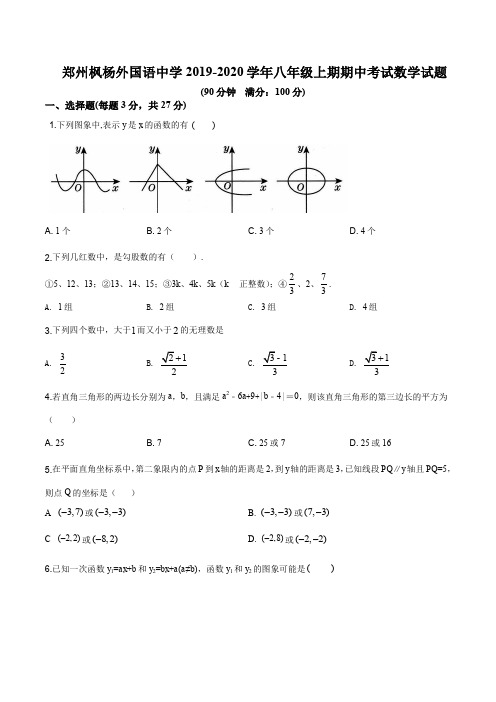
郑州枫杨外国语中学2019-2020学年八年级上期期中考试数学试题(90分钟 满分：100分)一、选择题(每题3分，共27分)1.下列图象中,表示y 是x 的函数的有 ()A. 1个B. 2个C. 3个D. 4个2.下列几红数中，是勾股数的有（ ）.①5、12、13；②13、14、15；③3k 、4k 、5k （k正整数）；④23、2、73. A. 1组 B. 2组 C. 3组 D. 4组3.下列四个数中，大于1而又小于2的无理数是 A. 32B. 12C. 13D. 13 4.若直角三角形的两边长分别为a ，b ，且满足a 2﹣6a +9+|b ﹣4|＝0，则该直角三角形的第三边长的平方为（ ）A. 25B. 7C. 25或7D. 25或165.在平面直角坐标系中，第二象限内的点P 到x 轴的距离是2，到y 轴的距离是3，已知线段PQ ∥y 轴且PQ =5，则点Q 的坐标是（ ）A . (3,7)-或(3,3)--B. (3,3)--或(7,3)- C (2,2)-或(8,2)- D. (2,8)-或(2,2)--6.已知一次函数y 1=ax +b 和y 2=bx +a (a ≠b )，函数y 1和y 2的图象可能是( )A.B. C. D. 7.点M1，-2)关于x 轴对称的点所在的象限是 ( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限8.0)a <得( ) AB.D. 9.小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练，他们从同一地点出发，先到达终点的人原地休息，已知小明先出发2秒，在跑步的过程中，小明和小亮的距离y (米)与小亮出发的时间t (秒)之间的函数关系如图所示，下列四种说法：①小明的速度是4米/秒；②小亮出发100秒时到达了终点； ③小明出发125秒时到达了终点；④小亮出发20秒时，小亮在小明前方10米．其中正确的说法为( )A. ①②③B. ②③④C. ①②④D. ①②③④二、填空题(每题3分，共21分)10.在34，2π，0，223-，0.454454445…，中，无理数有______个． 11.已知关于x 函数224(5)1m y m x m -=-++，若它是一次函数，则m =______.12.将一次函数y ＝5x ﹣1的图象向上平移3个单位，所得直线不经过第_____象限．13.如图所示，把边长为1的正方形放在数轴上，以数1表示的点为圆心，正方形的对角线长为半径作弧，交数轴于点A ，则点A 表示的数是_____．14.已知x 、y 为实数，且满足12y =求521x y +-15.如图，ABCD 是长方形地面，长AB ＝10m ，宽AD ＝5m ，中间竖有一堵砖墙高MN ＝1m ．一只蚂蚱从点A 爬到点C ，它必须翻过中间那堵墙，则它至少要走______m ．16.如图，矩形ABCD 中，AB ＝6，BC ＝8，点E 是BC 边上一点，连接AE ，把∠B 沿AE 折叠，使点B 落在点B ′处，当△CEB ′为直角三角形时，BE 的长为_____．三、解答题(共52分)17.计算题2(--(2) ()()110101132π-⎛⎫-+-+ ⎪⎝⎭18.先化简，再求值.(6(4-，其中x y ==19.已知一次函数y=kx+b 的图象经过点（﹣2，5），并且与y 轴交于点P ，直线y=12x+3与y 轴交于点Q ，点Q 恰与点P 关于x 轴对称，求这个一次函数的解析式． 20.如图，在△ABC 中，∠B =90°，AB =BC =9，把△ABC 进行折叠，使点A 与点D 重合，BD :DC =1:2，折痕为EF ，点E 在AB 上，点F 在AC 上，求EC 的长.21.甲、乙两车分别从相距420km 的A 、B 两地相向而行，乙车比甲车先出发1小时，两车分别以各自的速度匀速行驶，途经C 地（A 、B 、C 三地在同一条直线上）．甲车到达C 地后因有事立即按原路原速返回A 地，乙车从B 地直达A 地，甲、乙两车距各自出发地的路程y （千米）与甲车行驶所用的时间x （小时）的关系如图所示，结合图象信息回答下列问题：（1）甲车的速度是 千米/时，乙车的速度是 千米/时； （2）求甲车距它出发地的路程y （千米）与它行驶所用的时间x （小时）之间的函数关系式； （3）甲车出发多长时间后两车相距90千米？请你直接写出答案．22.如图直线l ：y ＝kx +6与x 轴、y 轴分别交于点B 、C 两点，点B 的坐标是（﹣8，0），点A 的坐标为（﹣6，0）．（1）求k 的值．（2）若点P 是直线l 在第二象限内一个动点，当点P 运动到什么位置时，△PAC 的面积为3，求出此时直线AP 的解析式．（3）在x 轴上是否存在一点M ，使得△BCM 为等腰三角形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．。

一、选择题（每题3分，共24分）1. 如果一个实数的平方根与它的立方根相等，则这个数是（ ） A. 0 B. 正整数 C. 0和1 D. 12. 下列各组数中不是勾股数的一组是（ ）A. 7,24,25B. 4,6,9C. 0.3,0.4,0.5D. 114,7,8223. 点P （3,4）关于x 轴对称的点的坐标是（ ）A. ()34-，B. ()34，-C. ()34-，-D. ()4，3 4. 如果 ABC ∆的三边分别为()21,2,11m m m m --＞，那么（ ） A. ABC ∆是直角三角形，且斜边长为21m -； B. ABC ∆是直角三角形，且斜边长为2m ；C. ABC ∆是直角三角形，但斜边长需由m 的大小确定；D. ABC ∆不是直角三角形. 5. 下列说法错误的是（ ）A. a 2与()2a -相等 B. 2a 与()2a --互为相反数C.3a 与3a -互为相反数 D. a 与a -互为相反数6. 已知P （0，a ）在y 轴的负半轴上，则Q ()21,1a a ---+在（ ） A. y 轴的左边，x 轴的上方 B. y 轴的右边，x 轴的上方 C. y 轴的左边，x 轴的下方 D. y 轴的右边，x 轴的下方7. 化简二次根式22a a a+-的结果是（ ） A.2a -- B. 2a --- C.2a - D. 2a --8. 若一个三角形的三个内角度数之比为1:1:2，则它们所对的边的平方之比为（ ） A. 1:1:2 B. 1:2:4 C. 1:1:4 D. 2:1:1 二、填空题（每小题3分，共33分）9、x 为整数，且23x -≤≤，则x =__________.10、在数轴上与表示3-的点距离为1的点表示的数是__________. 11、若点(),P a b 在第三象限，则点()2,3M a b -+-在第__________象限.12、点C 在x 轴的下方，y 轴的右侧，距离x 轴三个单位长度，距离y 轴5个单位长度，则点C 的2017-2018学年郑州枫杨外国语中学八年级上学期数学第一次月考试卷蚂蚁AC 蜂蜜坐标___________.13、已知Rt ABC ∆中，C ∠=90°，若14a b cm +=，10c cm =，则Rt ABC ∆的面积__________2cm . 14、若215b +和31a -都是5的立方根，则23a b +=__________. 15、比较大小:1012-________89. (填“>”或“<”) 16、若()22a +与1b +互为相反数，则a b -的相反数为___________.17、如图，ABC ∆中，点A 的坐标为()0,1，点C 的坐标为()4,3，如果要使ABD ∆与ABC ∆全等，那么点D 的坐标是______________________.yxOCBA第17图 第18题图18、如图，圆柱形玻璃杯高为12cm ，底面周长为18cm ，在杯内离杯底4cm 的点C 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm 与蜂蜜相对的点A 处，则蚂蚁到达蜂蜜的最短距离为___________cm .19、在平面直角坐标系xoy 中，对于点(),P x y 我们把点()'1,1P y x -++叫做点P 的伴随点，已知点1A 的伴随点为2A ，点2A 的伴随点为3A ，点3A 的伴随点为4A ，这样依次得到123,,,nA A A A ，若点1A 的坐标为()3,1，则点3A 的坐标为________,点2014A 坐标为_______;若点1A 的坐标为(),a b ，对于任意的正整数n ，点n A 均在x 轴上方，则a ，b 应满足的条件为_________________. 三、解答题20、计算：（每题4分，共8分） （1）1(6215)363-⨯- （2）23332332(13)8(0.125)3-----⨯-马帅炮兵O xyCPAB21、（5分）如图所示，在象棋盘上建立平面直角坐标系，使“马”位于点（2,2），“炮”位点()1,2-，写出“兵”所在位置的坐标.22、（6分）设a,b,c 都是实数，且满足22(2)80a a b c c -+++++=,20ax bx c ++=,求式子22x x +的算术平方根.23、（7分）如图，在Rt ABC ∆中，90°C ∠=，5BC =,A ∠的平分线交BC 于点E ,EFAB ⊥于点F ，点F 恰好是AB 的一个三等分点(AF BF >)，求BE 的长.24、（7分）如图所示，(3,0)A -、(0,1)B 分别为x 轴、y 轴上的点，ABC ∆为等边三角形，点(3,)P a 在第一象限内，且满足2ABP ABC S S ∆∆=,求a 的值.25、（10分）如图1，等腰直角三角形ABC 中，90°BCA ∠=，AC CB =,点M,N 在边AB 上，且45°MCN ∠=.（1）如图○1，当AM BN =时，将ACM ∆沿CM 折叠，点A 落在P 处，再将BCN ∆沿CN 折叠，点B 也恰好落在P 点处，此时，PM AM =,PN BN =,PMN ∆的是形状是_______，线段AM 、BM 、MN 之间的关系是_______________________；（2）如图○2，当MCN ∠绕点C 在ACB ∠内部任意位置时，线段MN 、AM 、BN 之间的数量关系是____________.试证明你的猜想；若1,3AM BN ==，求MN 的长.CBM A N CB A M N （3）当MCN图○3的位置时，线段MN 、AM 、BN 之间的数量关系是____________.（不要求证明）图○1 图○2 图○3一、选择题1. A2. A3. B4. A5. D6. A7. B8. A 二、填空题9. 1-,0或1 10. 31--或31-+ 11. 四 12. ()5,3- 13. 24 14. 15 15. > 16.21- 17. ()4,1-，()1,1--或()1,3- 18. 15 19. ()3,1-，()0,2-，11a -<<和12b <<三、解答题20.（1）326523--；（2）32432-+ 21. 兵(2,3)- 22. 2 23. 3 24. 33 25.（1）等腰三角形，222AM BM MN += （2）222AM BN MN +=，MN =10 （3）222AM BN MN +=2017-2018学年郑州枫杨外国语中学八年级上学期数学第一次月考试卷答案。

郑州XX学校2017-2018学年上学期期中学业水平测试八年级数学试卷（考试时间：90分钟，满分：100分）一、选择题（每小题3分，共24分）1．在﹣2，，，3.14，，，这6个数中，无理数共有【】A．4个 B．3个C．2个 D．1个2．以下列数组作为三角形的三条边长，其中能构成直角三角形的是【】A．1，，3 B．，，5 C．1.5，2，2.5 D．，，3．在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是【】A． B． C．9 D．64．已知，则2xy的值为【】A．﹣15 B．15 C． D．5．在平面直角坐标系中，点P（﹣1，1）关于x轴的对称点在【】A．第一象限 B．第二象限 C．第三象限 D．第四象限6．若函数y=（m﹣1）x|m|﹣5是一次函数，则m的值为【】A．±1 B．﹣1 C．1 D．27．如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是【】A．乙前4秒行驶的路程为48米B．在0到8秒内甲的速度每秒增加4米/秒C．两车到第3秒时行驶的路程相等D．在4至8秒内甲的速度都大于乙的速度8．若实数a、b、c满足a+b+c=0，且a＜b＜c，则函数y=ax+c的图象可能是【】A．B．C．D．二、填空题（每小题3分，共21分）9．的算术平方根是．10．如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为．11．在△ABC中，AB=10，AC=2，BC边上的高AD=6，则另一边BC等于12．在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1y2．（填“＞”“＜”或“=”）13．小明到超市买练习本，超市正在打折促销：购买10本以上，从第11本开始按标价打折优惠，买练习本所花费的钱数y（元）与练习本的个数x（本）之间的关系如图所示，那么在这个超市买10本以上的练习本优惠折扣是折．14．如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，则CE的长为．15．观察下列各式：…请你将发现的规律用含自然数n（n≥1）的等式表示出来．三、解答题（共7小题，共55分）16．计算（8分）：（1）×（9）（2）﹣×．17．（6分）已知2a+1的平方根是±3，5a+2b﹣2的算术平方根是4，求：3a﹣4b的平方根．18．（6分）如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．（1）试判断△BDE的形状，并说明理由；（2）若AB=4，AD=8，求△BDE的面积．19．（9分）△ABC在直角坐标系内的位置如图所示．（1）分别写出A、B、C的坐标；（2）请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称，并写出B1的坐标；（3）请在这个坐标系内画出△A2B2C2，使△A2B2C2与△ABC关于原点对称，并写出A2的坐标．20．（8分）如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：（1）△ACE≌△BCD；（2）AD2+DB2=DE2．21．（9分）已知一次函数y=2x+4（1）在如图所示的平面直角坐标系中，画出函数的图象；（2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；（3）在（2）的条件下，求出△AOB的面积；（4）利用图象直接写出：当y＜0时，x的取值范围．22.（9分）在社会主义新农村建设中，某乡镇决定对A、B两村之间的公路进行改造，并有甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：（1）乙工程队每天修公路多少米？（2）分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式．（3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？八年级数学试卷参考答案一、选择题（每小题3分，共24分）1．C． 2．C． 3．A． 4．A． 5．C． 6．B． 7．C． 8．A．二、填空题（每小题3分，共21分）9．9． 10．﹣1． 11．6或10． 12．＜． 13．七．14．． 15．=（n+1）（n≥1）．三、解答题（共7小题，共55分）16．计算：（1）原式 = ×9× = 45；（2）原式 =﹣ = 1﹣．17．解：根据题意得：2a+1=32=9，5a+2b﹣2=16，即a=4，b=﹣1，∴3a﹣4b=16，∴3a﹣4b的平方根是±=±4．答：3a﹣4b的平方根是±4．18．解：（1）△BDE是等腰三角形．由折叠可知，∠CBD=∠EBD，∵AD∥BC，∴∠CBD=∠EDB，∴∠EBD=∠EDB，∴BE=DE，即△BDE是等腰三角形；（2）设DE=x，则BE=x，AE=8﹣x，在Rt△ABE中，由勾股定理得：AB2+AE2=BE2即42+（8﹣x）2=x2，解得：x=5，所以S△BDE=DE×AB=×5×4=10．19．解：（1）A（0，3）；B（﹣4，4）；C（﹣2，1）；（2）如图：B1的坐标为：（4，4）；（3）如图：A2（0，﹣3）．20．证明：（1）∵∠ACB=∠ECD=90°，∴∠ACD+∠BCD=∠ACD+∠ACE，即∠BCD=∠ACE．∵BC=AC，DC=EC，∴△ACE≌△BCD．（2）∵△ACB是等腰直角三角形，∴∠B=∠BAC=45度．∵△ACE≌△BCD，∴∠B=∠CAE=45°∴∠DAE=∠CAE+∠BAC=45°+45°=90°，∴AD2+AE2=DE2．由（1）知AE=DB，∴AD2+DB2=DE2．21．解：（1）当x=0时y=4，当y=0时，x=﹣2，则图象如图所示（2）由上题可知A（﹣2，0）B（0，4），（3）S△AOB=×2×4=4，（4）x＜﹣2．22．解：（1）由图得：720÷（9﹣3）=120（米）答：乙工程队每天修公路120米．（2）设y乙=120x+b，把点（3,0）代入，得b=-360.所以y乙=120x﹣360，当x=6时，y乙=360，设y甲=kx，把点（6,360）代入，则360=6k，k=60，所以y甲=60x；（3）当x=15时，y甲=900，所以该公路总长为：720+900=1620（米），设需x天完成，由题意得：（120+60）x=1620，解得：x=9，答：该项工程由甲、乙两工程队一直合作施工，需9天完成．。

一、选择题1．题目文件丢失！2．题目文件丢失！3．题目文件丢失！4．题目文件丢失！5．题目文件丢失！6．题目文件丢失！7．题目文件丢失！8．题目文件丢失！9．题目文件丢失！10．题目文件丢失！11．题目文件丢失！12．题目文件丢失！13．题目文件丢失！14．题目文件丢失！15．题目文件丢失！二、填空题16．题目文件丢失！17．题目文件丢失！18．题目文件丢失！19．题目文件丢失！20．题目文件丢失！21．题目文件丢失！22．题目文件丢失！23．题目文件丢失！24．题目文件丢失！25．题目文件丢失！三、解答题26．题目文件丢失！27．题目文件丢失！28．题目文件丢失！29．题目文件丢失！30．题目文件丢失！【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．B2．C3．C4．A5．C6．D7．A8．C9．B10．A11．A12．D13．C14．D15．C二、填空题16．2n-1【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3以及A2B2=2B1A2得出A3B3=4B1A2=4A4B4=8B1A2=8A5B5=16B1A2…进而得17．66【解析】【分析】首先根据正五边形的性质得到度然后根据角平分线的定义得到度再利用三角形内角和定理得到的度数【详解】解：∵五边形为正五边形∴度∵是的角平分线∴度∵∴故答案为：66【点睛】本题考查了多18．3【解析】【分析】分式的值为零时：分子等于零但是分母不等于零【详解】依题意得：x-3=0且x+3≠0解得x=3故答案是：3【点睛】本题考查了分式的值为零的条件分式值为零的条件是分子等于零且分母不等于19．3458【解析】【分析】根据此分式的值是正整数可知m-2是6的约数而6的约数是1236然后分别列出四个方程解之即可得出答案【详解】解：∵分式的值是正整数∴m-2＝1或2或3或6∴m＝3或4或5或8故20．或或【解析】分①4a2是平方项②4a2是乘积二倍项然后根据完全平方公式的结构解答解：①4a2是平方项时4a2±4a+1=（2a±1）2可加上的单项式可以是4a或-4a②当4a2是乘积二倍项时4a4+21．22【解析】【分析】底边可能是4也可能是9分类讨论去掉不合条件的然后可求周长【详解】试题解析：①当腰是4cm底边是9cm时：不满足三角形的三边关系因此舍去②当底边是4cm腰长是9cm时能构成三角形则22．6【解析】【分析】【详解】解：∵∠A+∠APO=∠POD+∠COD∠A=∠POD=60°∴∠APO=∠COD在△APO和△COD中∠A=∠CAPO=∠CODP=OD∴△APO≌△COD（AAS）∴A23．3【解析】在123处分别涂黑都可得一个轴对称图形故涂法有3种故答案为324．5【解析】【分析】根据非负数的性质列式求出mn的值然后代入代数式进行计算即可得解【详解】解：根据题意得：m-2=0n-2018=0∴m=2n=2018∴m-1+n0=12+1=32；故答案为：32【25．7【解析】【分析】把已知条件平方然后求出所要求式子的值【详解】∵∴∴=9∴=7故答案为7【点睛】此题考查分式的加减法解题关键在于先平方三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．B解析：解析丢失2．C解析：解析丢失3．C解析：解析丢失4．A解析：解析丢失5．C解析：解析丢失6．D解析：解析丢失7．A解析：解析丢失8．C解析：解析丢失9．B解析：解析丢失10．A解析：解析丢失11．A解析：解析丢失12．D解析：解析丢失13．C解析：解析丢失14．D解析：解析丢失15．C解析：解析丢失二、填空题16．2n-1【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3以及A2B2=2B1A2得出A3B3=4B1A2=4A4B4=8B1A2=8A5B5=16B1A2…进而得解析：解析丢失17．66【解析】【分析】首先根据正五边形的性质得到度然后根据角平分线的定义得到度再利用三角形内角和定理得到的度数【详解】解：∵五边形为正五边形∴度∵是的角平分线∴度∵∴故答案为：66【点睛】本题考查了多解析：解析丢失18．3【解析】【分析】分式的值为零时：分子等于零但是分母不等于零【详解】依题意得：x-3=0且x+3≠0解得x=3故答案是：3【点睛】本题考查了分式的值为零的条件分式值为零的条件是分子等于零且分母不等于解析：解析丢失19．3458【解析】【分析】根据此分式的值是正整数可知m-2是6的约数而6的约数是1236然后分别列出四个方程解之即可得出答案【详解】解：∵分式的值是正整数∴m-2＝1或2或3或6∴m＝3或4或5或8故解析：解析丢失20．或或【解析】分①4a2是平方项②4a2是乘积二倍项然后根据完全平方公式的结构解答解：①4a2是平方项时4a2±4a+1=（2a±1）2可加上的单项式可以是4a或-4a②当4a2是乘积二倍项时4a4+解析：解析丢失21．22【解析】【分析】底边可能是4也可能是9分类讨论去掉不合条件的然后可求周长【详解】试题解析：①当腰是4cm底边是9cm时：不满足三角形的三边关系因此舍去②当底边是4cm腰长是9cm时能构成三角形则解析：解析丢失22．6【解析】【分析】【详解】解：∵∠A+∠APO=∠POD+∠COD∠A=∠POD=60°∴∠APO=∠COD在△APO和△COD中∠A=∠CAPO=∠CODP=OD∴△APO≌△COD（AAS）∴A解析：解析丢失23．3【解析】在123处分别涂黑都可得一个轴对称图形故涂法有3种故答案为3解析：解析丢失24．5【解析】【分析】根据非负数的性质列式求出mn的值然后代入代数式进行计算即可得解【详解】解：根据题意得：m-2=0n-2018=0∴m=2n=2018∴m-1+n0=12+1=32；故答案为：32【解析：解析丢失25．7【解析】【分析】把已知条件平方然后求出所要求式子的值【详解】∵∴∴=9∴=7故答案为7【点睛】此题考查分式的加减法解题关键在于先平方解析：解析丢失三、解答题26．解析丢失27．解析丢失28．解析丢失29．解析丢失30．解析丢失。

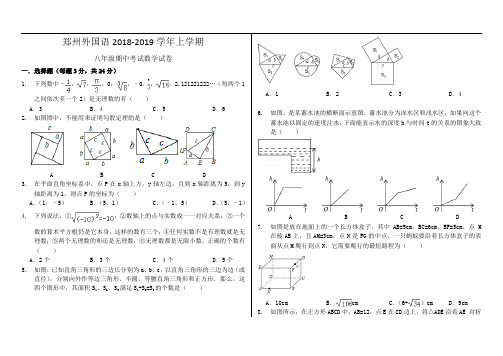
郑州市枫杨外国语中学 2018−2019 学年八年级上期第二次月考数学试卷(时间：90 分钟，满分：100 分)一、选择题(3 分×9=27 分)1. 在下列各数：3. 14，−π， 5 ，A.2B.3C. 4D.5，131，3 27中无理数的个数是()112. 下列关系中：y =−3x +1、y =3、y =x 2+1、y =1x ，y 是x 的一次函数的有()x 2A.1个B.2个C.3个D. 4个3. 下列命题中，是假命题的是( )A. 等腰三角形时轴对称图形B. 无理数都是小数C. 有一个角等于 60°的等腰三角形是等边三角形D. 两边分别相等且其中一组等边的对角相等的两个三角形全等4. 已知 a =5，=7，且a +b =a +b ，则a −b 的值为( )A. 2或12B. 2或−12C. −2或12D. −2或−125. 某校有15名同学参加区数学竞赛.已知有8名同学获奖，他们的竞赛得分均不相同.若知道某位同学的得分，要判断它能否获奖，在下列15名同学成绩的统计量中， 只需知道( )A. 方差B. 平均数C.众数D.中位数6. 如图，在△ABC 中，若 AB =AC =6，BC =4，D 是 BC 的中点，则 AD 的长等于 ()第6题图A. 4B. 2C. 2D. 47. 如图，在四边形ABCD 中，AB =12cm ，BC =3cm ，CD =4cm ，∠C =90°，当为多少时? ∠ABD =90°( ) A.13B.6C. 12D.6第7题图8. 若点P (m ，1)在第二象限内，则点Q (1−m ，−1)在( )A. 第三象限B.x 轴负半轴上C.第四象限D. y 轴负半轴上9. 已知A 、B 两地相距180km ，甲、乙两车分别从A 、B 两地同时出发，匀速开往对方所在地.甲车的速度是90km /h ，乙车的速度是60km /h ，甲、乙两车之间的距离y (km )与时间x (h )的函数图象是()A. B. C.⎨x -2y =m +1 二、填空题(3 分×9=27 分)10. 若4-a有意义，则a 的取值范围为 . a + 211. 如图，若∠1=∠D =39°，∠C =51°，则∠B =°. 12. 若x +17的立方根是3，则3x −5的立方根是.13. 比较大小： -1 5 +1 (填“>”“<”或“=”).14. 已知点(−4，y 1) (2，y 2)都在直线 y =1x + 2 上，则 y 12y 2(填“>”“<”或“=”).15.已知点M (a ，−4)与点N (6，b )关于直线x =2对称，那么a −b 等于.16.已知关于 x 、y 的二元一次方程组⎧x +y =5-m，⎩则4x 2−4xy +y 2的值为 .17.如图，矩形ABCD 中AB =6，BC =10，将矩形如图折叠，折痕为BE ，若点A 的对应点F 恰好落在线段EC 上，则折痕BE 的长为 .18.如图，在平面直角坐标系中矩形 AOBC 的顶点 A ，B 的坐标分别第17题图是A (0，2)，B (2，0)，做点A 关于直线y =kx (k >0)的对称点P ，△POB 为等腰三角形，则点P 的坐标为 .三、解答题(共46分) 19.计算(每题 5分，共 10分)⎧3x - 2(y -1)= 11 ⑴ 18⨯(-1)-3-64-6-32+1-⎪ ⑵ ⎨x +y= 3 ⎩4 320. (8分)某射击队教练为了了解队员的训练情况，从队员中选取甲、乙两名队员进行射击测试，相同条件下各射击 5次，成绩统计如下表：⑴根据上述信息可知：甲命中环数的中位数是环，乙命中环数的众数是环；⑵试通过计算说明甲、乙两人的成绩谁比较稳定； ⑶如果乙再射击1次，命中8环，那么乙射击成绩的方差会(填“变大”、“变小”或“不变”)21.(8分)如图，已知 AD ⊥BC ，EF ⊥BC ，垂足分别是 D 、F ，∠1=∠2，∠3=110°，试求∠BAC 的度数.第21题图22.(8分)俗话说：“冬至到，吃饺子”随着中国传统节日“冬至”的临近，丹尼斯百货决定开展“喜迎冬至，回馈顾客”的让利促销活动，对部分品牌的水饺进行打折销售，其中甲品牌水饺打八折，乙品牌水饺打七五折. 已知打折后，买6盒品牌水饺和3盒乙品牌水饺需117元；打折前，买50盒甲品牌水饺和40盒乙品牌水饺需1550元.⑴打折前，每盒甲、乙品牌水饺分别是多少元?⑵阳光敬老院需购买甲品牌水饺80 盒，乙品牌水饺100 盒，则打折后购买这批水饺比打折前节省了多少钱?23.(12分)如图，在平面直角坐标系中，△AOB为等边三角形，B(4，0)，直线l：y=kx+b经过点B，点C是x轴上点B右侧的一动点，以线段AC为边在第一象限作等边△ACD.⑴直接写出点A的坐标.当直线l经过点A时，求直线BA的表达式.⑵当直线l 经过点D 时，直线l 与y 轴相交于点F，随着点C 的变化，点F 的位置是否发生变化?若没有变化，求出此时点F 的坐标；若有变化，请说明理由.⑶当直线l 与线段OA 相交于点E 时，如果直线l 把△AOB 的面积分为1:2 两部分，求出此时点E 的坐标.⑷若点C 的坐标为(8，0)时，直线l 与线段AD 有交点，请直接写出此时k 的取值范围.⎨⎨y ＝80郑州市枫杨外国语中学 2018−2019 学年八年级上期第二次月考数学试卷答案参考一、选择题 1.B 2.B 3.D 4.D 5.D 6. A 7. A 8.C 9.D二、填空题10. a≤4且a≠-211.129 12.±5 13.< 14.< 15.2 16.36. 17.218. ( 2 3 ， 2 33 )，( 2 3 ，- 233 )，( 2，2)，( 2，-2).3 3 三、解答题19. 解：⑴3- 3 3 3⎧x =6 ⎪ ⎨y =9⎩⎪ 220. 解：⑴8 环，6 或 9 环；⑵甲的平均数是：(7+8+8+8+9)÷5=8 ，则甲的方差是： 1[(7-8)2+3(8-8)2+(9-8)2]=0.4，5 乙的平均数是：(6+6+9+9+10)÷5=8 ，则甲的方差是： 1[2(6-8)2+2(9-8)2+(10-8)2]=2.8，5所以甲的成绩比较稳定；⑶如果乙再射击 1 次，命中 8 环，那么乙的射击成绩的方差变小．故答案为：变小． 21. 解：70°.22. 解：⑴设打折前甲品牌粽子每盒 x 元，乙品牌粽子每盒 y 元， 根据题意得： ⎧6x + 3y ＝660⎩50⨯0.8x +40⨯0.75y ＝5200，解得：⎧x ＝70．⎩ 答：打折前甲品牌粽子每盒 70 元，乙品牌粽子每盒 80 元． ⑵80×70× (1-80%)+100×80× (1-75%)=3120(元)． 答：打折后购买这批粽子比不打折节省了 3120 元．23. 解：⑴A(2，2 3 )，直线 AB 的解析式为：y=- 3 x+4 3 ； ⑵作直线 BD ，由已知 AO=AB ，AC=AD ，又∵∠OAB=∠CAD ， ∴∠OAB+∠BAC=∠CAD+∠BAC ，即∠OAC=∠BAD ，∴△OAC ≌△BAD(SAS)∠AOC=∠ABD=60°， ∵∠OAB=∠AOB=60°，∴∠OAB=∠ABD=60°，∴BD ∥OA ，∵直线OA 的解析式为y ＝-3x ，设直线BD ：y ＝3x+b 1， 则0＝3×4+b 1，所以b 1=−43，即点 F 的位置不会发生变化，为 F(0，−4 3 )．⑶有两种情况，当OE= 1 3 OA 或 OE′= 2 3OA 时，满足条件， ∵A(2，2 3 )，∴E( 1 ， 3 )，E′( 2 ， 2 3)；3 3 3 3 ⑷k≤- 3 或 k≥ 3 .⑵。

郑州2017-2018学年上学期期中考试卷八年级 数学一、选择题：（每题3分，共30分）1.下列四个数中，是负数的是 （ ） A.2- B.()22- C.2- D.()22-2.在下列各数中， 212212221.1,27,2,216,21,8,0,46,31,32.0,733-∏--（相邻两个1之间的2的个数逐步增加1），499，其中无理数的个数是（ ） A.3个 B.4个 C.5个 D.6个3.若直角三角形三边长6,8，m ，则2m 的值为 （ ）A.10B.100C.28D.100或284.在,12,9,90,0===∠∆BC AC C ABC Rt 则点C 到斜边AB 的距离是（ ） A. 536 B.512 C.9 D.6 5.若,27b a -且a,b 是连续的整数，则a+b= （ ）A.1B.2C.3D.46.如图，OA=OB,BD=1,则数轴上点A 表示的是 （ ） A.2 B.3 C.5 D.107.若点P （m ，1）在第二象限内，则Q （-m ，O ），在 （ ）A.x 轴正半轴B.x 轴负半轴C.y 轴正半轴D.y 轴负半轴8.下列函数，满足下面两个条件的是：①y 随x 的增大而减小； ②与y 轴正半轴相交 （ ）A. y=-2x-1B.y=-2x+1C.y=2x-1D.y=2x+19.已知函数()321-+=m x m y ，是正比例函数，且过二，四象限，则m （ ）A.2B.-2C.2±D.21- 10.a ，b 在数轴上位置如图，化简：2a b a -- （ ）A.2a-bB.bC.-bD.-2a+b二、填空题：（每题3分，共15分）11.等腰求底边上的高底边腰,16,10==∆BC AB ABC 。

12.已知点P （-3,2），A 和P 关于y 轴对称，则A 坐标。

13.点p 在第四想先，且到x 轴距离是4，到y 轴距离是3，则点p 的坐标。

14.比较大小：5223。

郑州XX学校2017-2018学年上学期期中学业水平测试八年级数学试卷（考试时间：90分钟，满分：100分）一、选择题（每小题3分，共24分）1．在﹣2，，，3.14，，，这6个数中，无理数共有【】A．4个 B．3个C．2个 D．1个2．以下列数组作为三角形的三条边长，其中能构成直角三角形的是【】A．1，，3 B．，，5 C．1.5，2，2.5 D．，，3．在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是【】A． B． C．9 D．64．已知，则2xy的值为【】A．﹣15 B．15 C． D．5．在平面直角坐标系中，点P（﹣1，1）关于x轴的对称点在【】A．第一象限 B．第二象限 C．第三象限 D．第四象限6．若函数y=（m﹣1）x|m|﹣5是一次函数，则m的值为【】A．±1 B．﹣1 C．1 D．27．如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是【】A．乙前4秒行驶的路程为48米B．在0到8秒内甲的速度每秒增加4米/秒C．两车到第3秒时行驶的路程相等D．在4至8秒内甲的速度都大于乙的速度8．若实数a、b、c满足a+b+c=0，且a＜b＜c，则函数y=ax+c的图象可能是【】A．B．C．D．二、填空题（每小题3分，共21分）9．的算术平方根是．10．如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为．11．在△ABC中，AB=10，AC=2，BC边上的高AD=6，则另一边BC等于12．在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1y2．（填“＞”“＜”或“=”）13．小明到超市买练习本，超市正在打折促销：购买10本以上，从第11本开始按标价打折优惠，买练习本所花费的钱数y（元）与练习本的个数x（本）之间的关系如图所示，那么在这个超市买10本以上的练习本优惠折扣是折．14．如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C 恰好落在AD边上的点F处，则CE的长为．15．观察下列各式：…请你将发现的规律用含自然数n （n≥1）的等式表示出来．三、解答题（共7小题，共55分）16．计算（8分）：（1）×（9）（2）﹣×．17．（6分）已知2a+1的平方根是±3，5a+2b﹣2的算术平方根是4，求：3a﹣4b的平方根．18．（6分）如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．（1）试判断△BDE的形状，并说明理由；（2）若AB=4，AD=8，求△BDE的面积．19．（9分）△ABC在直角坐标系内的位置如图所示．（1）分别写出A、B、C的坐标；（2）请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称，并写出B1的坐标；（3）请在这个坐标系内画出△A2B2C2，使△A2B2C2与△ABC关于原点对称，并写出A2的坐标．20．（8分）如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：（1）△ACE≌△BCD；（2）AD2+DB2=DE2．21．（9分）已知一次函数y=2x+4（1）在如图所示的平面直角坐标系中，画出函数的图象；（2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；（3）在（2）的条件下，求出△AOB的面积；（4）利用图象直接写出：当y＜0时，x的取值范围．22.（9分）在社会主义新农村建设中，某乡镇决定对A、B两村之间的公路进行改造，并有甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：（1）乙工程队每天修公路多少米？（2）分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式．（3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？八年级数学试卷参考答案一、选择题（每小题3分，共24分）1．C． 2．C． 3．A． 4．A． 5．C． 6．B． 7．C． 8．A．二、填空题（每小题3分，共21分）9．9． 10．﹣1． 11．6或10． 12．＜． 13．七．14．． 15．=（n+1）（n≥1）．三、解答题（共7小题，共55分）16．计算：（1）原式 = ×9× = 45；（2）原式 =﹣ = 1﹣．17．解：根据题意得：2a+1=32=9，5a+2b﹣2=16，即a=4，b=﹣1，∴3a﹣4b=16，∴3a﹣4b的平方根是±=±4．答：3a﹣4b的平方根是±4．18．解：（1）△BDE是等腰三角形．由折叠可知，∠CBD=∠EBD，∵AD∥BC，∴∠CBD=∠EDB，∴∠EBD=∠EDB，∴BE=DE，即△BDE是等腰三角形；（2）设DE=x，则BE=x，AE=8﹣x，在Rt△ABE中，由勾股定理得：AB2+AE2=BE2即42+（8﹣x）2=x2，解得：x=5，所以S△BDE=DE×AB=×5×4=10．19．解：（1）A（0，3）；B（﹣4，4）；C（﹣2，1）；（2）如图：B1的坐标为：（4，4）；（3）如图：A2（0，﹣3）．20．证明：（1）∵∠ACB=∠ECD=90°，∴∠ACD+∠BCD=∠ACD+∠ACE，即∠BCD=∠ACE．∵BC=AC，DC=EC，∴△ACE≌△BCD．（2）∵△ACB是等腰直角三角形，∴∠B=∠BAC=45度．∵△ACE≌△BCD，∴∠B=∠CAE=45°∴∠DAE=∠CAE+∠BAC=45°+45°=90°，∴AD2+AE2=DE2．由（1）知AE=DB，∴AD2+DB2=DE2．21．解：（1）当x=0时y=4，当y=0时，x=﹣2，则图象如图所示（2）由上题可知A（﹣2，0）B（0，4），（3）S△AOB=×2×4=4，（4）x＜﹣2．22．解：（1）由图得：720÷（9﹣3）=120（米）答：乙工程队每天修公路120米．（2）设y乙=120x+b，把点（3,0）代入，得b=-360.所以y乙=120x﹣360，当x=6时，y乙=360，设y甲=kx，把点（6,360）代入，则360=6k，k=60，所以y甲=60x；（3）当x=15时，y甲=900，所以该公路总长为：720+900=1620（米），设需x天完成，由题意得：（120+60）x=1620，解得：x=9，答：该项工程由甲、乙两工程队一直合作施工，需9天完成．。

学年上学期第二次考试试题郑州2017-2018数学八年级分钟）（满分：100分时间：903选择题（每小题分,共30分）一．（）1．下列各数中，不是无理数的是?7）…（相邻两个5之间1A. 的个数逐次加 B. 0.5 C. 21 D. 0.5151151115，则斜边长是（）2.直角三角形的两条直角边长分别为3，4D．2 B. 3 C．4 A．）3. 下列说法错误的是（1 的平方根是±1 B. –1的立方根是– A. 122)3(? C. 是是2的算术平方根 D. -3的平方根）3，那么点P的坐标为（，到P在第四象限内，P到x轴的距离是4y轴的距离是4. 点 -4） D.（3，（-3,4） C. （4，-3）A.（-4,3）B.?5?x?6，且x 若是整数，则满足条件的x的值有（） 5.A.5个 B.4个 C.3个D.2个x?1mx?ny?7??是二元一次方程组的解，则m的值为（6.已知）??y?1nx?my?1??A.1 B.2 C.3 D.4已知一次函数y=kx-k,若y随x的增大而增大,则图象经过（）7.A.第一?二?三象限B.第一?三?四象限C.第一?二?四象限D.第二?三?四象限8．八年级1班生活委员小华去为班级购买两种单价分别为8元和10元的盆栽，共有100元，若小华将100元恰好用完，共有几种购买方案（）A. 2B.3C. 4D.59.在平面直角坐标系中，点A(2，m)在第一象限，若点A关于x轴的对称点B在直线y=-x+1上，则m的值为( )A.-1B.1C.2D.310．如图，正方形ABCD的边长为2，动点P从C出发，在正方形的边上沿着C→B→A的方向运动(点P与A不重合)．设P运动的路程为x，则下列图象中符合△ADP的面积y关于x的函数关系式的是()15分）二．填空题（每小题3分,共45?20。

计算：11.= 轴对称，则点B的坐标为。

B），点A与点关于y12.已知点A（-2，-3．平面直角坐标系内的一条直线同时满足下列两个条件：①不经过第四象限；②与两条坐标轴所13 2，这条直线的解析式可以是（写出一个解析式即可）．围成的三角形的面积为AB为8，宽A与C重合．若长方形的长BCABCD14．如图，把长方形纸片折叠，使其对角顶点，则折痕EF的长度为。

P BA 6第6题图AB HGFE D 43C第7题图第8题图AF E D CB郑州外国语中学2017-2018八年级上期期中考试数学试卷(时间：90分钟，满分：100分)一、选择题(3分×8=24分)1. 在下列各数：3. 14159260. 2、1π13111A . 2个B . 3个C . 4个D . 5个2. 已知点P (a ，b )到x 轴的距离是2，到y 轴的距离是5，且a b a b -=-， 则P 点的坐标是（）A . (5，2)B . (2，−5)C . (5，2)或(5，−2)D . (2，−5)或(5，2) 3. 下列说法正确的有（）①无理数是无限不循环小数；②1的平方根与立方根都是1④负数的立方根仍是负数；⑤3±. A . 2个B . 3个C . 4个D . 5个4. 如图，爸爸从家(点O )出发，沿着等腰三角形AOB 的边OA →AB →BO 的路 径去匀速散步，其中OA =OB . 设爸爸距家(点O )的距离为S ，散步的时间为t ， 则下列图形中能大致刻画S 与t 之间函数关系的图像是（）A .B .C .D .5. 点P在数轴上运动，它所对应的数值为a ，如图，当点P 从点A 运动到点B ， 4a +的最大值为（）A . 5B . a +1C . 7D . a +46. 如图所示，AE ⊥AB ，且AE =AB ，BC ⊥CD 且BC =CD ，若点 E 、B 、D 到直线AC 的距离分别为6，3，4，则图中实现所围 成的图像面积是（） A . 50B . 44C . 38D . 327. 如图，圆柱形容器的底面周长是30cm ，高为17cm ，在外侧地面S处有 一蜘蛛，与蜘蛛相对的圆柱形容器的上口内侧距开口出3cm 的点F 处有 一苍蝇，急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是（） A. B . 25cmC.D . 30cm8. 如图，在直角坐标系中，已知点P 0的坐标为，将线段OP 0按逆时针 方向旋转45°，再将其长度伸长为OP 0的2倍，得到线段OP 1；又将线段OP 1逆时针方向旋转45°，长度伸长为OP 1的2倍，得到线段OP 2线段OP 3，OP 4，…，OPn (n 为正整数)，则点P 2017的坐标为（）A 2017220172)B . (0，22018)C 2018220182)D. (22018，0) 二、填空题(3分×7=21分) 9. 填“>”、“=”、“<”) 10. 化简()113.1412π-⎛⎫-+- ⎪⎝⎭的结果________.11. 4，则点A (1，a )关于y 轴的对称点为B ，则点B 的坐标为___________.12. 当m =______时，函数23()23my m x -=-+是关于x 的一次函数.13. 如图，在长方形ABCD 中，DC =6cm ，在DC 上存在一点E ，沿直线AE 把三角形AE 折叠，使点D 恰好落在BC 边上，设此点为F ，若三角形ABF 的面积为24，那么CE 长度为__________cm 2.14. 在东昌湖举行的健身运动会龙舟比赛中，甲、乙两队在500米的赛道上，所滑行的路程y (m )与实践x (min )之间的函数关系如图所示，下列说法正确 的有____________.①乙队比甲队提前0. 25min 到达终点. ②当乙队划行110m 时，此时落后甲队15m . ③0. 5min 后，乙队比甲队每分钟快40m .④自1. 5min 开始，甲队若要与乙队同时到达终点，甲队的速度需要提高到255m /min . 15. 在△ABC 中，AB =10，AC =17，BC 边上的高为8，则△ABC 的面积为__________.DCBA备用图三、解答题(共55分)16. 计算：(每题4分，共8分)252-(2)()((201720182231⎛---⎝17. (5分)已知2a+4的立方根是−2，3a+b−1的算数平方根是1的整数部分是c，求3a+b−c的值.18. (6分)如图，图中的小方格都是边长为1的正方形，若点A(−x，362y-+)，点B(2x−1，213y+)，点C(z+1，283z-)，已知点A，B关于原点对称，点C在二，四象限平分线上.(1)求A、B、C点的坐标；(2)结合A、B、C的坐标，在图中建立平面直角坐标系；(3)在(2)的条件下，若P为y轴上的一个动点，请直接写出使△PBC周长最小的点P的坐标.19. (6分)观察下列各式：①()1f=；②()2f=③()3f=()4f=(1)利用你观察到的规律直接写出f(n)=________________；(2)计算()()()()()21232017f f f f⎡++++⎤⎣⎦.20. (8分)某工厂加工一批汽车零件，为了提前交货，规定每个工人完成规定每个工人完成100个以内(含100个)，每个零件付酬1. 8元；超过100个，超过部分每个零件付酬增加0. 2元；超过200个，超过部分除按上述规定外，每个零件再增加0. 5元.(1)若一个工人加工了150个零件，他能得到多少报酬?(2)求一个工人所得报酬y(元)与零件数x(个)之间的函数关系式.21. (10分)如图，△ABC和△DBE都是等腰直角三角形，点D在AC上，其中∠ABC=∠DBE=90°.(1)求∠DCE的度数；(2)当AB=5，AD：DC=2：3时，求DE的大小；(3)当点D在线段AC上运动时(D不与A重合)，请写出一个反映DA2，DC2，DB2之间关系的等式，并加以证明.22. (12分)如图，在平面直角坐标系内，点O为坐标原点，点A在x轴负半轴上，点B、C分别在x轴、y轴正半轴上，且OB=2OA，OB−OC=OC−OA=1.(1)求点C的坐标；(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动，同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动，当点Q到达终点A时，点P、Q均停止运动，设点P运动的时间为t(t＞0)秒，线段PQ的长度为y，用含t的式子表示y，并写出相应的t的范围；(3)在(2)的条件下，过点P作x轴的垂线PM，PM=PQ，是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.郑州外国语中学2017-2018八年级上期期中考试数学试卷答案参考一、选择题1. A2. C3. B4. D5. C6. A7. B8. B 二、填空题9. >10. 11. (-1，-1) 或(-1，7) 12. -2 13. 8314. ①②③ 15. 36或84 三、解答题 16. ⑴17. 解：由题意得，248311a a b +=-+-=⎧⎨⎩，解得620a b =-=⎧⎨⎩，3，即c =3，则3a +b -c =-6×3+20-3=-1， ∴3a +b -c =-1.18. ⑴A (-1,-3)、B (1，3)、C (2，-2)； ⑵如右图所示： ⑶P (0，43). 19. ⑴f (n;⑵2017.20. ⑴280元；⑵分类讨论①y =1.8x （x ≤100）；②y =1.8x +（x ﹣100）×0.2=2x -20（100<x ≤200）； ③y =2.5x -120 （x >200）．21. 解:⑴由SAS ，手拉手结构，△ABD ≌△CBE ，∴∠A =∠ACB =∠BCE =45°， ∠ABD =∠CBE ，AD =CE ，DB =BE ，∴∠PCQ =∠ACB +∠BCQ =90°，∠ABP +∠PBC =∠CPQ +∠PBC =90°， ∴△BDE 是等腰直角三角形，△DCE 是直角三角形；⑵当AB =5，AD ：DC =2:3时，有AC=AD=DC= 于是，在Rt △DCE 中，CD=CE =AD=DE⑶存在，2BD 2=DA 2+DC 2；由于△BDE 是等腰直角三角形,∴DE，∵AD =CE ，∴DE 2=DC 2+CE 2=AD 2+CD 2， 故2BD 2=AD 2+CD 2.22. 解：（⑴∵点A 在x 轴负半轴上，点B 、C 分别在x 轴、y 轴正半轴上，OB =2OA ，OB -OC =OC -OA =2． 设A （x ，0），∴OA =-x ，OB =-2x ，OC =-2x -2，∴B （-2x ，0），C （0，-2x -2）， ∵OC -OA =2，∴-2x -2-（-x ）=2，解得：x =-4， ∴OA =4，OB =8，OC =6，点A 的坐标为（-4，0），点B 的坐标为（8，0），点C 的坐标为（0，6）； ⑵由⑴知：AB =OA +OB =12，∵点P 从点A 出发以每秒1个单位的速度沿AB 向点B 匀速运动，同时点Q 从点B 出发以每秒3个单位的速度沿BA 向终点A 匀速运动，∴点P 运动的时间为t （t ＞0）秒时，AP =t ，BQ =3t ， 当P 、Q 两点相遇时的t 的值为：12÷（1+3）=3秒，∵当点Q 到达终点A 时，点P 、Q 均停止运动， ∴t 的最大值为12÷3=4秒； ①当0＜t ≤3时，如图1，PQ =AB -AP -QB =12-t -3t =12-4t ， 即y =12-4t （0＜t ≤3）； ②当3＜t ≤4时，如图2， PQ =AP +BQ -AB =4t -12， 即y =4t -12（3＜t ≤4）；⑶存在t 值使点O 为PQ 中点， ∵点O 为PQ 中点，∴0＜t ≤3，OP =OQ ，即OA -AP =OB -BQ ，∴4-t =8-3t ，解得：t =2， 当t =2时，AP =2，OP =2，OQ =2，PQ =4，PM =PQ =4， ①点M 在x 轴上方时，如图3，过点C 作CN ⊥PM ，得：四边形CNPQ 是梯形， ∵S △CMQ =S 梯形CNPQ -S △CNM -S △PQM ， ∴S △CMQ =12(CN +PQ )×PN -12CN •MN -12•PM •PQ =12×(OP +PQ )×OC -12×OP ×（OC -PM ）-12×4×4 =12×(2+4)×6-12×2×(6-4)-8 =18-2-8=8；②点M 在x 轴下方，如图4．过点C 作CN ⊥PM ，得：四边形CNPQ 是梯形， ∵S △CMQ =S 梯形CNPQ +S △PQM -S △CNM ， ∴S △CMQ =12（CN +PQ ）•PN +12•PQ •PM -12•MN •CN =12×（OP +PQ ）×OC +12×4×4-12•（OC +PM ）•OP =12×（2+4）×6+8-×（6+4）×2 =12×6×6+8-12×10×2 =18+8-10=16．∴三角形CMQ 的面积为：8或16．。