甘肃省武威第六中学2020-2021学年高二上学期第二次学段考试数学(理)试题 Word版含答案

正视图322甘肃省武威市第六中学2020-2021学年高二数学上学期第二次学段考试试题 文一、选择题：本大题共12小题，每小题5分，共计60分．请把答案填写在答题卷相应位置．．．．．．．上．． 1．命题“已知a ，b ，c 为实数，若abc ＝0，则a ，b ，c 中至少有一个等于0”，则该命题的逆命题、否命题、逆否命题中，真命题的个数为（ ） A ．0B ．1C ．2D ．32．直线21l //l ,在1l 上取3个点,2l 上取2个点,由这5个点能确定平面的个数为（ ） A.5 B.4 C.9 D.1 3．命题“∃x 0∈（0，+∞）．lnx 0＝x 0+1”的否定是（ ） A ．∃x 0∈（0，+∞）．lnx 0≠x 0+1 B ．∀x ∉（0，+∞）．lnx ≠x +1 C ．∀x ∈（0，+∞）．lnx ≠x +1D ．∃x 0∉（0，+∞）．lnx 0≠x 0+14．若方程2244x ky k +=表示焦点在y 轴上的椭圆，则实数k 的取值范围为 A ．(4,)+∞B ．(0,4)C ．(,4)-∞D ． (,0)-∞5．条件p ：关于x 的不等式（a ﹣4）x 2+2（a ﹣4）x ﹣4＜0（a ∈R ）的解集为R ；条件q ：0＜a ＜4，则p 是q 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．给出两个命题：p ：函数y ＝x 2－x －1有两个不同的零点；q ：若1x <1，则x>1，那么在下列四个命题中，真命题是( ) A ． (￢p)∨(￢q) B ．p ∧q C ．(￢p)∧(￢q)D ．(￢p)∨q7．如图，α∩β＝l ，点A ，C ∈α，点B ∈β，且BA ⊥α，BC ⊥β，那么直线l 与直线AC 的关系是( )A ．异面B ．平行C ．垂直D ．不确定8．若正四棱锥的正视图和俯视图如图所示，则该几何体的表面积是（ ） A ．4 B ．4410+ C ．8 D ．4411+9．设球的体积为V ，它的内接正方体的体积为V ，下列说法中最合适的是（ ）A ． V 比V 大约多一半；B ． V 比V 大约多两倍半；C ． V 比V大约多一倍； D ． V 比V大约多一倍半10．用a,b,c 表示三条不同的直线,γ表示平面,给出下列命题: ①若a ∥b,b ∥c,则a ∥c; ②若a ⊥b,b ⊥c,则a ⊥c; ③若a ∥γ,b∥γ,则a ∥b; ④若a ⊥γ,b⊥γ,则a ∥b. 其中真命题的序号是( ) A.①②B.②③C.①④D.③④11．已知直线的斜率为2,、是直线与双曲线C :,的两个交点,设、的中点为(2,1),则双曲线C 的离心率为( ) A.B.C. 2D.12．已知函数f （x ）＝ ， g （x ）＝2x +a ，若对任意的∈[-1，2]，总存在∈[﹣1，2]，使得f （）=g （），则实数a 的取值范围是（ ） A ．[﹣1，1] B ．（﹣∞，﹣1]∪[1，+∞） C ．[﹣1，2]D ． [3，+∞）二、填空题：本大题共4小题，每小题5分，共计20分．请把答案填写在答题卷相应位置上．．．．．．．．． 13．下列说法正确的序号是 ①经过三点时以确定一个平面；②梯形可以确定一个平面；③两两相交的三条直线最多可以确定三个平面；④如果两个平面有三个公共点，则这两个平面重合.14．若命题“∃x ∈[0，3]，使得x 2﹣ax +3＜0成立”是假命题，则实数a 的取值范围是 ．（用区间写）15．若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积之比为 .16．设F 1，F 2是双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左，右焦点，O 是坐标原点．过F 2作C 的一条渐近线的垂线，垂足为P .若|PF 1|＝6|OP |，则C 的离心率为_____三、解答题：本大题共6小题，共计70分．请在答题卷指定区域内作答．．．．．．．．．．，解答时应写出文字说明、证明过程或计算步骤．17．(本题10分)已知p :x 2-2x +2≥m 的解集为R ;q :函数f (x )=-(7-3m )x是减函数.若这两个命题中有且只有一个是真命题,求实数m 的取值范围.18．（本小题满分12分）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，PA ⊥底面ABCD ，且PA AD =，点F 是棱PD 的中点，点E 为CD 的中点．（1）证明：∥EF 平面PAC ； （2）证明：AF EF ⊥．19.（本小题满分12分）已知抛物线219:2C y x =与双曲线222:13y C x -=在第一象限的交点为P ，斜率为2的直线l 过点P ．（1）求双曲线2C 的渐近线方程及离心率； （2）求直线l 被抛物线1C 所截得的弦长．20．（本题12分）如图，已知正方体ABCD ­A 1B 1C 1D 1，O 是底面ABCD 对角线的交点．求证：(1)C 1O ∥面AB 1D 1； (2)A 1C ⊥面AB 1D 1.21. (本题12分)在如图所示的多面体中,已知是正三角形,是的中点．(1)求证：平面；(2)求直线与平面所成角的余弦值；22．(本题12分)已知为椭圆的左右焦点，点为其上一点，且有(Ⅰ)求椭圆的标准方程；(Ⅱ)过的直线与椭圆交于两点，过与平行的直线与椭圆交于两点，求四边形的面积的最大值.高二文科数学答案一，选择题DDCBBACBDCAA二，填空题 13.②③ 14.15.16.三，解答题17.【答案】若命题p 为真命题,由x 2-2x +2=(x -1)2+1≥m ,可知m ≤1; 若命题q 为真命题,则7-3m >1,即m <2.命题p 和q 中有且只有一个是真命题,则p 真q 假或p 假q 真,即或,所以1<m <2故实数m 的取值范围是(1,2) 18．（本小题满分12分）【解析】（1）点,E F 分别为,CD PD 的中点，∥EF PC ∴，（2分）PC ⊂平面PAC ，EF ⊄平面PAC ， ∥EF ∴平面PAC .（4分）（2）PA ⊥平面ABCD ，CD ⊂平面ABCD ，CD PA ∴⊥，又四边形ABCD 是矩形，CD AD ∴⊥，PA AD A =，CD 平面PAD ，（8分）AF ⊂平面PAD ，AF CD ∴⊥，PA AD =，点F 是PD 的中点，AF PD ∴⊥，又CDPD D =， AF ∴⊥平面PDC ，（10分）EF ⊂平面PDC ，AF EF ∴⊥.（12分）19．（本小题满分12分）【答案】（1）3y x =，离心率为2；（2）1558． 【解析】（1）令2203y x -=，可得双曲线2C 的渐近线方程为3y x =，（2分）双曲线2C 的离心率221132be a=+=+=．（4分） （2）将292y x =与2213y x -=联立，消去2y 可得22320x x --=，解得2x =（负值舍去），因为点P 位于第一象限，所以(2,3)P ，（6分）因为斜率为2的直线l 过点P ，所以直线l 的方程为32(2)y x -=-，即21y x =-，（7分）将21y x =-代入292y x =，消去y 可得281720x x -+=， 设直线l 与抛物线1C 交于11(,)A x y ，22(,)B x y 两点，则12178x x +=，1214x x =，（10分）所以直线l 被抛物线1C 所截得的弦长221212155||1()4AB k x x x x =+⋅+-=．（12分）20.[证明] (1)如图，连接A 1C 1，设A 1C 1∩B 1D 1＝O 1，连接AO 1， ∵ABCDA 1B 1C 1D 1是正方体， ∴A 1ACC 1是平行四边形， ∴A 1C 1∥AC 且A 1C 1＝AC ，又O 1，O 分别是A 1C 1，AC 的中点， ∴O 1C 1∥AO 且O 1C 1＝AO ， ∴四边形AOC 1O 1是平行四边形，∴C 1O ∥AO 1，AO 1⊂面AB 1D 1，C 1O ⊄面AB 1D 1， ∴C 1O ∥面AB 1D 1. (2)∵CC 1⊥面A 1B 1C 1D 1， ∴CC 1⊥B 1D 1， 又∵A 1C 1⊥B 1D 1， ∴B 1D 1⊥面A 1C 1CA ，即A 1C ⊥B 1D 1，同理可证A 1C ⊥AB 1， 又B 1D 1∩AB 1＝B 1，∴A 1C ⊥面AB 1D 1.21.解析：(1)如图,取的中点,连接,因为的中点,所以MF∥,又AF∥DE,所以MF∥,四边形为平行四边形.所以,因为平面平面,所以平面(2)因为是正三角形,所以,在中,,所以,故,又所以平面取的中点,连接,则,又,所以,又,所以平面,所以是直线与平面所成的角．在中,所以22.【答案】(Ⅰ)设椭圆的标准方程为因为，根据椭圆的性质得，所以又因为点在椭圆上，所以解得所以椭圆的标准方程为.(Ⅱ)由题意可知，四边形为平行四边形，所以=4设直线的方程为，且，由代入化简可得，由根与系数的关系可得：，因为=+，所以====令，则，==，又因为在上单调递增，所以，所以的最大值为,所以的最大值为6.。

甘肃省武威第六中学2021-2022高二数学下学期第二次学段考试（期末考试）试题 文（含解析）一、单选题（每小题5分，共60分）1. 已知集合M ＝{x|(x －1)2＜4，x∈R}，N ＝{－1，0，1，2，3}，则M∩N＝（ ）A. {0，1，2}B. {－1，0，1，2}C. {－1，0，2，3}D. {0，1，2，3}【答案】A【解析】试题分析：求出集合M 中不等式的解集，确定出M ，找出M 与N 的公共元素，即可确定出两集合的交集．解：由（x ﹣1）2＜4，解得：﹣1＜x ＜3，即M={x|﹣1＜x ＜3}，∵N={﹣1，0，1，2，3}，∴M∩N={0，1，2}．故选A点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2. 若命题p 的逆命题是q ，否命题是r ，则q 是r 的（ ）A. 逆命题B. 否命题C. 逆否命题D. 以上都不正确【答案】C【解析】【分析】首先设原命题p 为：若m 则n ，分别求出逆命题是q 和否命题是r ，再判断即可得到答案.【详解】设原命题p 为：若m 则n ，则逆命题q 为：若n 则m ，否命题r 为：若m ⌝则n ⌝. 则q 是r 的逆否命题.故选：C【点睛】本题主要考查四种命题，熟练掌握四种命题的关系为解题的关键，属于简单题.3. 若4sin 5α，且α为锐角，则sin 2α的值等于（ ）.A. 1225B. 2425C. 1225-D. 2425- 【答案】B【解析】【分析】根据二倍角的正弦公式计算即可. 【详解】4sin 5α=,α为锐角, 3cos 5α∴=, 4324sin 22sin cos 25525ααα∴==⨯⨯=, 故选：B【点睛】本题主要考查了同角三角函数的基本关系，二倍角的正弦公式，属于容易题.4. “a 、b 、c 成等比数列”是“b =） A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件 【答案】D【解析】【分析】利用充分条件和必要条件的定义结合等比中项的定义判断即可.【详解】充分性：若a 、b 、c 成等比数列，则2b ac =且0ac >，则b =成立；必要性：若b =0a b c ===，则a 、b 、c 不成等比数列，即必要性不成立.因此，“a 、b 、c 成等比数列”是“b =. 故选：D.【点睛】本题考查充分条件、必要条件的判断，同时也考查了等比中项定义的应用，考查计算能力与推理能力，属于基础题.5. 函数sin cos y x x =⋅的最小正周期和最大值分别为（ ）A. π，1B. π，12C. 2π，1D. 2π，12 【答案】B【解析】【分析】利用二倍角公式进行化简，进而可得函数sin cos y x x =⋅的最小正周期和最大值. 【详解】1sin cos =sin 22y x x x =⋅，函数sin cos y x x =⋅的最小正周期22T ππ==，1sin 21x -≤≤，∴111sin 2222x -≤≤，∴函数sin cos y x x =⋅的最大值为12.故选：B.【点睛】本题考查了二倍角公式、最小正周期及正弦型函数的最值问题，属于基础题.6. 已知5log 2a =，0.5log 0.2b =，0.20.5c =，则,,a b c 的大小关系为（ ）A. a c b <<B. a b c <<C. b c a <<D. c a b <<【答案】A【解析】【分析】 利用10,,12等中间值区分各个数值的大小．【详解】551log 2log 2a =<，0.50.5log 0.2log 0.252b =>=，10.200.50.50.5<<，故112c <<，所以a c b <<．故选A ．【点睛】本题考查大小比较问题，关键选择中间量和函数的单调性进行比较．7. 函数()21,11,1x x x f x x x⎧-+<⎪=⎨>⎪⎩的值域为（ ） A. 3,4⎡⎫+∞⎪⎢⎣⎭ B. ()0,1 C. 3,14⎡⎫⎪⎢⎣⎭D. ()0,∞+ 【答案】D【解析】【分析】分别求出当1,1x x <>时的值域,再取并集即可.【详解】当1x <时,2213()1()24f x x x x =-+=-+,故3(),,(1)4f x x ⎡⎫∈+∞<⎪⎢⎣⎭.当1x >时,1()(0,1)f x x =∈,故()21,11,1x x x f x x x ⎧-+<⎪=⎨>⎪⎩的值域为()0,∞+.故选D【点睛】分段函数的值域只需每段函数单独求解值域再求并集即可.8. 函数()22x x xf x -=+的大致图象为（ ）A. B.C. D.【答案】B【解析】【分析】根据函数为奇函数排除C ，取特殊值排除AD 得到答案. 【详解】当()22x x x f x -=+，()()22x x x f x f x ---==-+，函数为奇函数，排除C ； 2221(2)22242f -=<=+，排除A ； 3324(3)22536f -==+，4464(4)224257f -==+，故()()34f f >，排除D. 故选：B.【点睛】本题考查了函数图象的识别，意在考查学生的计算能力和识图能力，取特殊值排除是解题的关键.9. 若函数()f x ax b =+的零点是2（0a ≠），则函数2()g x ax bx =+的零点是（ ）A. 2B. 2和0C. 0D. 2-和0【答案】B【解析】【分析】 首先根据()f x 的零点是2求得,a b 的关系式，对()g x 因式分解，由此求得()g x 的零点.【详解】由条件知(2)0f =，∴2b a =-，∴2()(2)g x ax bx ax x =+=-的零点为0和2.故选B.【点睛】本小题主要考查函数零点的知识运用，属于基础题.10. 已知全集U =R ，设函数()lg 1y x =-定义域为集合A ，函数y =的值域为集合B ，则()U AC B =（ ） A. [)1,3B. []1,3C. ()1,3D. (]1,3 【答案】C【解析】 ∵全集U=R ，设函数y=lg （x ﹣1）的定义域为集合A ，∴A={x|x﹣1＞0}={x|x ＞1}，∵函数y =的值域为集合B ， ∴B={y|y∴C U B={y|y ＜3}，∴A∩（∁U B ）=（{x|1＜x ＜3}=（1，3）．故选C ．11. 函数()f x 定义在0,2π⎛⎫⎪⎝⎭上，()f x '是它的导函数，且()()tan x f x f x '⋅>在定义域内恒成立，则（ ）A. 43f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭ 63f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭C. ()cos1126f f π⎛⎫⋅>⎪⎝⎭ 46ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭【答案】D【解析】【分析】 构造函数()cos (),0,2g x x f x x π⎛⎫=⋅∈ ⎪⎝⎭，利用所给不等式判断()'g x 的符号推出()g x 的单调性，利用()g x 的单调性即可比较函数值的大小. 【详解】因为0,2x π⎛⎫∈ ⎪⎝⎭，所以sin 0cos 0x x >>，， 由()()tan x f x f x '⋅>可得()cos ()sin f x x f x x '<，即()cos ()sin 0f x x f x x '-<， 令()cos (),0,2g x x f x x π⎛⎫=⋅∈ ⎪⎝⎭，则()()cos ()sin 0g x f x x f x x ''=-<， 所以函数()g x 在0,2π⎛⎫ ⎪⎝⎭上为减函数，则(1)643g g g g πππ⎛⎫⎛⎫⎛⎫>>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 则cos cos cos(1)(1)cos 664433f f f f ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫>>> ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，2cos(1)(1)643f f πππ⎛⎫⎛⎫⎛⎫>>>⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选：D 【点睛】本题考查利用导数研究函数的单调性、函数单调性的应用，属于中档题.12. 已知()f x 是定义域为(),-∞+∞的奇函数，满足()()2f x f x =-.若()11f =，则()()()()1232019f f f f +++⋅⋅⋅+=（ ）A. -2021B. 1C. 0D. 2021【答案】C【解析】【分析】推导出函数()f x 为周期为4的周期函数， ()11f =，(2)(02)(0)0,(3)(12)(1) 1.(4)(0)0,f f f f f f f f =+=-==+=-=-== 由此能求出()()()()1232019.f f f f +++⋅⋅⋅+ 【详解】 ()f x 是定义域为(),-∞+∞的奇函数，满足()()2f x f x =-，则有()()2f x f x -=+ ，又由函数()f x 为奇函数，则()()f x f x -=- ，则有(2)().f x f x +=- ∴ (4)(2)f x f x +=-+ ∴ (4)().f x f x +=则函数()f x 是周期为4的周期函数，()11f ∴=，(2)(02)(0)0,(3)(12)(1) 1.(4)(0)0,f f f f f f f f =+=-==+=-=-==∴ ()()()()[]1232019504(1)(2)(3)(4)(1)(2)(3)50401010.f f f f f f f f f f f +++⋅⋅⋅+=⨯++++++=⨯++-=【点睛】本题考查了函数的奇偶性，周期性．通过函数的奇偶性和周期性推导出函数的周期是关键．第II 卷（非选择题）二、填空题（每小题5分，共20分） 13. 240432(3)(3)log 6427π-+-+-=__________.【答案】1【解析】【分析】根据指数幂运算及对数的性质,化简即可求解.【详解】根据指数幂运算及对数的性质,化简可得240432(3)(3)log 6427π-+-+-()2633231log 23=-++-31691=++-=.故答案为:1【点睛】本题考查了指数幂运算及对数的性质应用,属于基础题.14. 已知()2log ,0,21,0,x x x f x x ->⎧=⎨-+<⎩则方程()3f x =的解是x =______. 【答案】8【解析】【分析】采用分类讨论进行求解，结合对数方程以及指数方程的解法，可得结果.【详解】由题可知：①208log 3x x x >⎧⇒=⎨=⎩，②0213x x x -<⎧⇒∈∅⎨-+=⎩故方程()3f x =的解是8x =故答案为：8【点睛】本题考查根据分段函数解析式，给出函数值求解，关键在于分类讨论方法的使用，审清题意，细心计算，属基础题.15. 函数2()34f x x mx =-+在[5,)-+∞上是增函数，在(,5]-∞-上是减函数，则(1)f -=_________．【答案】23-【解析】【分析】根据二次函数单调性确定m 的值，代入函数求解函数值.【详解】函数2()34f x x mx =-+在[5,)-+∞上是增函数，在(,5]-∞-上是减函数， 所以5,306m m =-=-，2()3304f x x x =++， (1)330423f -=-+=-.故答案为：23-【点睛】此题考查根据函数单调性求参数的取值，根据函数解析式求解函数值，属于简单题目.16. 若()323ln 442f x m x x x x =-+-+在()2,+∞上单调递减，则实数m 取值范围__________.【答案】(],20-∞【解析】【分析】由题可知，求导()2334m f x x x x'=-+-，由于()f x 在()2,+∞上单调递减，则转化为()0f x '≤在()2,+∞上恒成立，分离参数法，转化为32334m x x x ≤-+在()2,+∞上恒成立，构造新函数()()323342g x x x x x =-+>，利用导数研究函数的单调性和最值，求出()min g x 即可得出m 取值范围.【详解】解：()323ln 442f x m x x x x =-+-+()0x >， ()2334m f x x x x'∴=-+-， 由于()f x 在()2,+∞上单调递减，即()0f x '≤在()2,+∞上恒成立， 即23340m x x x-+-≤在()2,+∞上恒成立， 则32334m x x x ≤-+在()2,+∞上恒成立，即()min m g x ≤在()2,+∞上恒成立，设()()323342g x x x x x =-+>， ()2964g x x x '=-+，知364940∆=-⨯⨯<，()2,x ∴∈+∞时，()0g x '>，()g x 单调递增，()()32min 232324220m g x g ∴≤==⨯-⨯+⨯=，20m ∴≤，即实数m 取值范围为(],20-∞.故答案为：(],20-∞.【点睛】本题考查利用导数研究函数的单调性求参数范围，以及利用函数解决恒成立问题，考查转化思想和计算能力.三、解答题（共70分）17. 已知:p 22a -<<，q ：关于x 的方程20x x a -+=有实数根.（1）若q 为真命题，求实数a 的取值范围；（2）若p q ∨为真命题，q ⌝为真命题，求实数a 的取值范围.【答案】（1）14a ≤；（2）124a << 【解析】【分析】（1）关于x 的方程x 2﹣x+a=0有实数根，则△=1﹣4a≥0，解得a 的范围．（2）由题意得p 为真命题，q 为假命题求解即可.【详解】（1）方程20x x a -+=有实数根，得：:140q a ∆=-≥得14a ≤； （2）p q ∨为真命题，q ⌝为真命题∴ p 为真命题，q 为假命题，即2214a a -<<⎧⎪⎨>⎪⎩得124a <<. 【点睛】本题考查了一元二次方程的实数根与判别式的关系、复合命题真假的判断方法，考查了推理能力，属于基础题．18. 已知()()()()3sin cos 2cos 2cos sin 2f ππαπαααπαπα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭. (1)化简()f α；(2)若α是第三象限角，且()1sin 5απ-=，求()f α的值. 【答案】(1)()cos f αα=-. 【解析】【分析】(1)根据诱导公式直接化简即可;(2)由()1sin 5απ-=,可以利用诱导公式计算出sin α,再根据角所在象限确定cos α,进而得出结论.【详解】(1)根据诱导公式 ()()()()3sin cos 2cos 2cos sin 2f ππαπαααπαπα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭()sin cos sin sin sin ααααα⋅⋅-=⋅ cos α=-,所以()cos f αα=-;(2)由诱导公式可知()sin sin απα-=-,即1sin 5α=-, 又α是第三象限角,所以cos α==,所以()=cos 5f αα-=. 【点睛】本题主要考查诱导公式的运用,属于基础题.使用诱导公式时,常利用口诀“奇变偶不变,符号看象限”进行记忆.19. ()()()222f x x m x m m R =+--∈ (1)已知()f x 在[]2,4上是单调函数,求m 的取值范围；(2)求()0f x <的解集.【答案】(1) 6m ≤-或2m ≥-；(2) 当2m =-时,不等式()0f x <的解集为空集； 当2m >-时, 不等式()0f x <的解集为{}2x m x -<<；当2m <-时, 不等式()0f x <的解集为{}2x x m <<-.【解析】【分析】(1)求出函数的对称轴,然后根据二次函数的单调性,由题意分类讨论即可求m 的取值范围；(2)根据一元二次方程根之间的大小关系进行分类讨论求出()0f x <的解集.【详解】(1)函数 ()()()222f x x m x m m R =+--∈对称轴为：22m x -= 因为()f x 在[]2,4上是单调函数,所以有：242m -≥或222m -≤,解得 6m ≤-或2m ≥-；(2)方程()2220x m x m +--=的两个根为：2,m -. 当2m =-时,不等式()0f x <的解集为空集；当2m >-时, 不等式()0f x <的解集为{}2x m x -<<；当2m <-时, 不等式()0f x <的解集为{}2x x m <<-.【点睛】本题考查了已知函数单调性求参数问题,考查了求解一元二次不等式的解集,考查了分类讨论思想.20. 已知函数32111()2322f x x x x =---. （1）求函数()f x 的单调区间；（2）当[2,4]x ∈-时，求函数()f x 的最大值.【答案】（1）()f x 的单调增区间为(),1-∞-，()2,+∞；单调减区间为()1,2-（2）()max 296f x = 【解析】【分析】（1）函数()f x 求导数，分别求导数大于零小于零的范围，得到单调区间.（2）根据（1）中的单调区间得到最大值.【详解】解：（1）()22f x x x '=-- 当()0f x '>时，1x <-，或2x >；当()0f x '<时，12x -<<．∴()f x 的单调增区间为(),1-∞-，()2,+∞；单调减区间为()1,2-．（2）分析可知()f x 的递增区间是()2,1--，()2,4，递减区间是()1,2-，当1x =-时，()213f -=；当4x =时，()2946f =． 由于()()41f f >-，所以当4x =时，()max 296f x =． 【点睛】本题考查了函数单调区间，最大值，意在考查学生的计算能力.21. 已知函数2()(1)1()x f x mx x e m R =+-+∈.（1）当0m ≥时，讨论函数()f x 的单调性；（2）证明：当1,13x ⎛⎫∈ ⎪⎝⎭时，23()f x mx x >+. 【答案】（1）()f x 在(,0)-∞上单调递减，在(0,)+∞上单调递增；（2）证明见解析.【解析】【分析】（1）求出导数，判断导数符号从而确定单调性；（2）设()()23F x f x mx x =--，通过导数判断函数()F x 的单调性，证明()0F x >在1,13x ⎛⎫∈ ⎪⎝⎭上成立即可得证.【详解】（1）()()22x x f x mx xe x e m '=+=+，当0m ≥时，令()0f x '>，得0x >；令()0f x '<，得0x <，故()f x 在(,0)-∞上单调递减，在(0,)+∞上单调递增；（2）设233()()(1)1x F x f x mx x x e x =--=--+，则()2()(1)33x x x F x e x e x x e x '=+--=-，设()3x x e x ϕ=-，则()3x x e ϕ'=-， 1,13x ⎛⎫∈ ⎪⎝⎭，()30x e ϕ'∴<-<，()x ϕ∴在1,13⎛⎫⎪⎝⎭上单调递减，又1103ϕ⎛⎫=> ⎪⎝⎭，(1)30e ϕ=-<，()x ϕ∴在1,13⎛⎫ ⎪⎝⎭内存在唯一的零点，设为0x ，则当013x x <<时，()0x ϕ>，()0F x '>，()F x 单调递增，当01x x <<时，()0x ϕ<，()0F x '<，()F x 单调递减，又1133126226180327327e F e -⎛⎫=-=> ⎪⎝⎭，(1)0F =，()0F x ∴>在1,13x ⎛⎫∈ ⎪⎝⎭上成立，∴当1,13x ⎛⎫∈ ⎪⎝⎭时，23()f x mx x >+.【点睛】本题考查分类讨论含参函数的单调区间、利用导数证明不等式，属于较难题.22. 已知曲线4cos :3sin x C y θθ=⎧⎨=⎩（θ为参数）． （1）将C 的方程化为普通方程；（2）若点(,)P x y 是曲线C 上的动点，求2x y +的取值范围．【答案】（1）221169x y +=．（2）[． 【解析】【分析】（1）根据曲线的参数方程，消去参数ϕ，即可得到曲线的普通方程；（2）根据曲线的参数方程，求得28cos 3sin x y θθ+=+，再利用三角函数的性质，即可求解.【详解】解：（1）4:(3x cos C y sin θθθ=⎧⎨=⎩为参数)，所以1413x cos y sin θθ⎧=⎪⎪⎨⎪=⎪⎩，平方相加消除θ， 得曲线C 的普通方程为221169x y +=． （2）由曲线4cos :3sin x C y θθ=⎧⎨=⎩得823sin 8cos arctan 3x y θθθ⎛⎫+=+=+ ⎪⎝⎭ ∴当8sin arctan 13θ⎛⎫+= ⎪⎝⎭时，2x y +当8sin arctan 13θ⎛⎫+=- ⎪⎝⎭时，2x y +取得最小值 2x y ∴+的取值范围是[．【点睛】本题主要考查了参数方程与普通方程的互化，以及曲线的参数方程的应用，其中解答中掌握参数方程与普通方程的互化方法，以及合理利用曲线的参数方程是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.。

甘肃武威市六中2020年秋高二数学（理）上学期第二次学段考卷第I 卷（选择题）一、单选题（每小题5分，共60分） 1．抛物线24y x =的焦点坐标为（ ）A ．(1,0)-B ．(1,0)C ．(0,1)-D ．(0,1)2．设命题2:,10p x R x ∀∈+>，则p ⌝为（ ） A ．200,10x R x ∃∈+> B ．200,10x R x ∃∈+≤C ．200,10x R x ∃∈+<D ．200,10x R x ∃∈+<3．双曲线222536x y -＝1的渐近线方程为（ ）A ．6x ±5y =0B ．5x ±6y =0C ．25x ±36y =0D ．36x ±25y =04．已知函数()y f x =在0x x =处的导数为11，则()()000limx f x x f x x∆→-∆-=∆（ ）A ．11B ．-11C ．111 D ．111-5．“1x >”是“2x x >”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．设'()y f x =是函数()y f x =的导数，'()y f x =的图像如图所示， 则()y f x =的图像最有可能的是（ ）．A ．B ．C ．D ．7．已知l 是双曲线C ：22124x y -=的一条渐近线，P 是l 上的一点，F 1，F 2分别是C 的左，右焦点，若120PF PF ⋅=，则点P 到x 轴的距离为( )A ．233 B ．2 C ．2 D ．2638．已知A 、B 、C 是不共线的三点，O 是平面ABC 外一点，则在下列条件中，能得到点M 与A 、B 、C 一定共面的条件是（ ）A ．111222OM OA OB OC =++ B ．OM OA OB OC =++C ．1133OM OA OB OC =-+ D ．2OM OA OB OC =--9．设椭圆C ：22221x y a b +=(a >0，b >0)的左､右焦点分别为1F ，2F ，离心率为32.P 是C 上一点，且1F P⊥2F P .若12PF F △的面积为4，则a =（ ）A ．1B ．2C ．4D ．810．如图，棱长为1的正方体1111ABCD A B C D -，O 是底面1111D C B A 的中心，则O到平面11ABC D 的距离是（ ）A ．12 B ．24 C ．22D ．3211．过抛物线()220x py p =>的焦点F 作倾斜角为30°的直线，与抛物线交于A 、B 两点（点A 在y 轴左侧），则AFBF的值为（ ）A ．3B ．13C ．1D ．1212．已知()f x 是定义在R 上的偶函数，且()20f =，当0x >时，()()0xf x f x '->，则不等式()0xf x >的解集是( )A ．()(),22,-∞-+∞ B ．()2,2- C ．()()2,02,-+∞ D ．以上都不正确第II 卷（非选择题）二、填空题（每小题5分，共20分）13．若方程22151x y m m +=--表示焦点在y 轴的椭圆，则实数m 的取值范围是 .14．如图，在四棱柱1111ABCD A B C D -中，底面ABCD 是平行四边形，点E 为BD 的中点，若11A E xAA yAB zAD =++，则x y z ++=______. 15．给出下列命题：①“若1xy =，则lg lg 0x y +=”；②“若sin cos 3παα+=，则α是第一象限角”的否命题；③“若0b ≤，则方程2220x bx b b -++=有实根”的逆否命题； ④“若A B B ⋃=，则A B ⊆的逆命题． 其中是真命题的有________．16．设过原点的直线与双曲线C ：22221x y a b-=()0,0a b >>交于,P Q 两个不同点，F 为C 的一个焦点，若4tan 3PFQ ∠=，5QF PF =，则双曲线C 的离心率为__________.三、解答题：（共70分）17．已知函数()ln f x x =，()2g x ax bx =-（a 、b 为常数）.（1）求函数()f x 在点()()1,1f 处的切线方程；（2）当函数()g x 在2x =处取得极值2-，求函数()g x 的解析式.18．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD ，E 为PD 中点，O 为AC 中点，222AD AB AP ===.（1）证明：OE //平面PAB ；（2）异面直线PC 与OE 所成角的余弦值.19．已知抛物线()2:20E y px p =>的焦点F ，E 上一点坐标为()1,2.（1）求抛物线E 的方程；（2）过F 作直线l ，交抛物线E 于A ，B 两点，若直线AB 中点的纵坐标为1-，求直线l 的方程.20．如图，四边形ABCD 与BDEF 均为菱形，FA FC =，且60DAB DBF ∠=∠=︒.（1）求证：AC ⊥平面BDEF ；（2）求直线AD 与平面AEF 所成角的正弦值.21．已知函数()ln f x x x =-.（1）求()f x 的单调区间和极值；（2）若()(1)f x m x m -+≥对任意(0,)x ∈+∞恒成立，求实数m 的值.22．已知离心率为22的椭圆2222:1(0)x y C a b a b +=>>过点()2,1M．（1）求椭圆C 的方程；（2）过点()1,0作斜率为2直线l 与椭圆相交于A ，B 两点，求||AB 的长； （3）过点()1,0的直线l 与椭圆相交于A ，B 两点，求OAB ∆的面积的最大值．参考答案 一、选择题B 2．B 3．A 4．B 5．A 6．C 7．C 8．C 9．C 10．B 11．B 12．C 二、填空题13．(3,5) 14．0 15．③④ 162 三、解答题17．（1）由已知，(1)0f =，()'1f x x=，()'11f =，所以函数()f x 在点()()1,1f 处的切线方程为1y x =-，即10x y --=.（2）()'2g x ax b =-，由题意(2)0(2)2g g =⎧⎨=-'⎩，即40422a b a b -=⎧⎨-=-⎩，解得122a b ⎧=⎪⎨⎪=⎩，经检验，1,22a b ==满足题意，所以()2122g x x x =-.18．（1）证明：连接BD ，则O 为BD 中点， 又E 为PD 中点，∴OE //PB .∵PB ⊂平面PAB ，OE ⊄平面PAB ， ∴OE //平面PAB（2）以A 为原点建立空间直角坐标系， 如图，则(0,0,1),(1,2,0),(0,2,0)P C D ，110,1,,,1,022E O ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭∴11(1,2,1),,0,22PC OE ⎛⎫=-=- ⎪⎝⎭，∴3cos ,162PC OE ==⋅即异面直线PC 与OE 319．（1）把()1,2代入抛物线方程解得2P = ∴E 的方程为24y x =.（2）法一：由（1）得抛物线E 的方程为24y x =,焦点()1,0F设A ,B 两点的坐标分别为()11,Ax y ,()22,B x y ,代入抛物线可得则21122244y x y x ⎧=⎨=⎩,两式相减,整理得()211221214y y x x x x y y -=≠-+ ∵线段AB 中点的纵坐标为1-∴直线l 的斜率()2144212AB k y y ===-+-⨯直线l 的方程为()021y x -=--即220x y +-=法二：由（1）得抛物线E 的方程为24y x =,焦点()1,0F设直线l 的方程为1x my =+ 由241y x x my ⎧=⎨=+⎩消去x ,得2440y my --=设A ,B 两点的坐标分别为()11,Ax y ,()22,B x y ,∵线段AB 中点的纵坐标为1- ∴()124122m y y --+==- 解得12m =-直线l 的方程为112x y =-+即220x y +-= 20．（1）设AC 与BD 相交于点O ，连接FO ，∵四边形ABCD 为菱形，∴AC BD ⊥，且O 为AC 中点， ∵FA FC =，∴AC FO ⊥，又FO BD O ⋂=，∴AC ⊥平面BDEF（2）连接DF ，∵四边形BDEF 为菱形，且60DBF ∠=︒，∴DBF 为等边三角形，∵O 为BD 中点，∴FO BD ⊥，又AC FO ⊥， ∴FO ⊥平面ABCD .∵OA ，OB ，OF 两两垂直，∴建立空间直角坐标系O xyz -，如图所示，设2AB =，四边形ABCD 为菱形，60DAB ∠=︒，∴2BD =，23AC =∵DBF 为等边三角形， 3.OF =∴3,0,0)A ，()0,1,0B ，()0,1,0D -，3)F ∵DB EF =，//DB EF∴(0,E -(1,0AD =--，(AF =-，(0,2,0)EF =.设平面AEF 的法向量为(,,)n x y z =，则3020AF n x EF n y ⎧⋅=-=⎪⎨⋅==⎪⎩，取1x =，得()1,0,1n =. 设直线AD 与平面AEF 所成角为θ， 则||6sin cos ,4||||AD n AD n AD n θ⋅=<>==⋅. 21．（1）()ln f x x x =-，1()1f x x'=-，(0)x ∈+∞，， 由()0f x '>，得1x >，由()0f x '<，得01x <<， 所以()f x 在(01)，上单调递减，在(1)+∞，上单调递增， 所以()f x 有极小值(1)1f =，无极大值.（2）()ln (1)f x x x m x m =-≥-+即ln (1)0x m x --≤. 记()ln (1)h x x m x =--，则()0≤h x 对任意(0)x ∈+∞，恒成立， 求导得1()h x m x'=-（0x >）， 若0m ≤，则()0h x '>，得()h x 在(0)+∞，上单调递增，又(1)0h =， 故当1x >时，()0h x >，不合题意；若0m >，由()h x '0>得10x m <<，由()h x '0<得1x m>， 所以()h x 在10m ⎛⎫ ⎪⎝⎭，上单调递增，在1m ⎛⎫+∞ ⎪⎝⎭，单调递减. 依题意有max 1()ln 10()1h x h m m f m m ⎛⎫==--+⇔ ⎪⎝⎭≤≤，22．解：（1）由题可知，椭圆C 的离心率为2，且椭圆过点)M ，则222222211c e a a b a b c ⎧==⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得：24a =，222c b ==，故椭圆C 的方程为22142x y +=；（2）过点(1,0)作斜率为2直线l ，∴直线:22l y x =-，联立2214222x y y x ⎧+=⎪⎨⎪=-⎩，整理得：291640x x -+=， 设1(A x ，1)y ，2(B x ，2)y ，则12169x x +=，1249x x =， 2221212216164||()4535999AB x x x x ∴=+-=-=； （3）由于直线l 过点()1,0直线l ，设1(A x ，1)y ，2(B x ，2)y ， 当直线l 的斜率不存在时，直线l x ⊥轴，此时将1x =代入22142x y +=，解得：y =， 即A ，B的坐标分别为,1,⎛⎛ ⎝⎭⎝⎭，则OAB 的面积为：12111222S y y =-⨯==； 当直线l 的斜率存在，且不为0时，可设直线l 的方程为：1x my =+，联立221421x y x my ⎧+=⎪⎨⎪=+⎩，整理得：()222230m y my ++-=， 则12122223,11m y y y y m m --+==++， 而OAB 的面积为：12112S y y =-⨯=即S==12=== 令t =>2246t m =+，得 2264t m -=，所以(224426224t t S t t t t t ====>-+++，由于t >23t t +>=，则(422S t t t=<=>+所以综上得：2S ≤，所以OAB的面积最大值为2.。

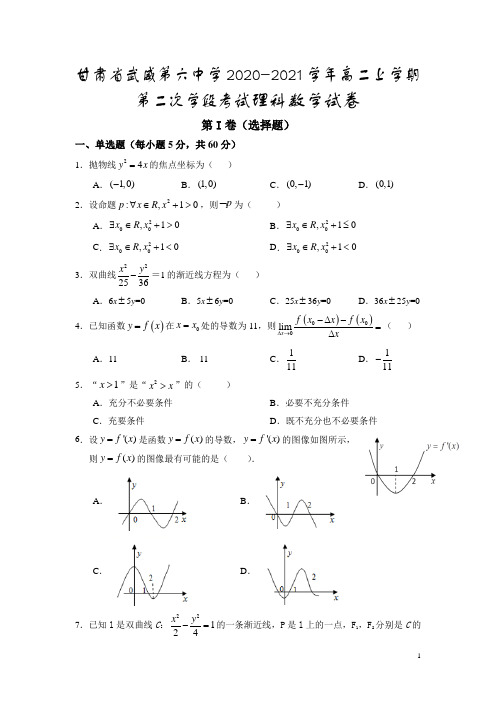
甘肃省武威第六中学2020-2021学年高二上学期第二次学段考试理科数学试卷第I 卷（选择题）一、单选题（每小题5分，共60分）1．抛物线24y x =的焦点坐标为（ ）A ．(1,0)-B ．(1,0)C ．(0,1)-D ．(0,1)2．设命题2:,10p x R x ∀∈+>，则p ⌝为（ ） A ．200,10x R x ∃∈+> B ．200,10x R x ∃∈+≤C ．200,10x R x ∃∈+<D ．200,10x R x ∃∈+<3．双曲线222536x y -＝1的渐近线方程为（ ）A ．6x ±5y =0B ．5x ±6y =0C ．25x ±36y =0D ．36x ±25y =04．已知函数()y f x =在0x x =处的导数为11，则()()000lim x f x x f x x∆→-∆-=∆（ ）A ．11B ．-11C ．111 D ．111-5．“1x >”是“2x x >”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．设'()y f x =是函数()y f x =的导数，'()y f x =的图像如图所示， 则()y f x =的图像最有可能的是（ ）．A ．B ．C ．D ．7．已知l 是双曲线C ：22124x y -=的一条渐近线，P 是l 上的一点，F 1，F 2分别是C 的左，右焦点，若120PF PF ⋅=，则点P 到x 轴的距离为( )A ．23B ．2C ．2D ．2638．已知A 、B 、C 是不共线的三点，O 是平面ABC 外一点，则在下列条件中，能得到点M 与A 、B 、C 一定共面的条件是（ ） A ．111222OM OA OB OC =++ B ．OM OA OB OC =++C ．1133OM OA OB OC =-+D ．2OM OA OB OC =--9．设椭圆C ：22221x y a b +=(a >0，b >0)的左､右焦点分别为1F ，2F ，离心率为3.P 是C 上一点，且1F P ⊥2F P .若12PF F △的面积为4，则a =（ ）A ．1B ．2C ．4D ．810．如图，棱长为1的正方体1111ABCD A B C D -，O 是底面1111D C B A 的中心，则O 到平面11ABC D 的距离是（ ）A ．12 B ．2 C ．2 D ．3211．过抛物线()220x py p =>的焦点F 作倾斜角为30°的直线，与抛物线交于A 、B 两点（点A 在y 轴左侧），则AFBF的值为（ ） A ．3 B ．13C ．1D ．1212．已知()f x 是定义在R 上的偶函数，且()20f =，当0x >时，()()0xf x f x '->，则不等式()0xf x >的解集是( )A ．()(),22,-∞-+∞ B ．()2,2- C ．()()2,02,-+∞D ．以上都不正确第II 卷（非选择题）二、填空题（每小题5分，共20分）13．若方程22151x y m m +=--表示焦点在y 轴的椭圆，则实数m 的取值范围是 .14．如图，在四棱柱1111ABCD A B C D -中，底面ABCD 是平行四边形，点E 为BD 的中点，若11A E xAA yAB zAD =++，则x y z ++=______. 15．给出下列命题：①“若1xy=，则lg lg 0x y +=”；②“若sin cos 3παα+=，则α是第一象限角”的否命题；③“若0b ≤，则方程2220x bx b b -++=有实根”的逆否命题； ④“若A B B ⋃=，则A B ⊆的逆命题． 其中是真命题的有________．16．设过原点的直线与双曲线C ：22221x y a b-=()0,0a b >>交于,P Q 两个不同点，F 为C 的一个焦点，若4tan 3PFQ ∠=，5QF PF =，则双曲线C 的离心率为__________.三、解答题：（共70分）17．已知函数()ln f x x =，()2g x ax bx =-（a 、b 为常数）.（1）求函数()f x 在点()()1,1f 处的切线方程；（2）当函数()g x 在2x =处取得极值2-，求函数()g x 的解析式.18．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD ，E 为PD 中点，O 为AC 中点，222AD AB AP ===. （1）证明：OE //平面PAB ；（2）异面直线PC 与OE 所成角的余弦值.19．已知抛物线()2:20E y px p =>的焦点F ，E 上一点坐标为()1,2.（1）求抛物线E 的方程；（2）过F 作直线l ，交抛物线E 于A ，B 两点，若直线AB 中点的纵坐标为1-，求直线l 的方程.20．如图，四边形ABCD 与BDEF 均为菱形，FA FC =，且60DAB DBF ∠=∠=︒.（1）求证：AC ⊥平面BDEF ；（2）求直线AD 与平面AEF 所成角的正弦值.21．已知函数()ln f x x x =-.（1）求()f x 的单调区间和极值；（2）若()(1)f x m x m -+≥对任意(0,)x ∈+∞恒成立，求实数m 的值.22．已知离心率为2的椭圆2222:1(0)x y C a b a b +=>>过点)M．（1）求椭圆C 的方程；（2）过点()1,0作斜率为2直线l 与椭圆相交于A ，B 两点，求||AB 的长； （3）过点()1,0的直线l 与椭圆相交于A ，B 两点，求OAB ∆的面积的最大值．武威六中2020-2021学年度第一学期 第二次学段考试高二数学试卷（理）参考答案一、选择题B 2．B 3．A 4．B 5．A 6．C 7．C 8．C 9．C 10．B 11．B 12．C 二、填空题13．(3,5) 14．0 15．③④ 162 三、解答题17．（1）由已知，(1)0f =，()'1f x x=，()'11f =，所以函数()f x 在点()()1,1f 处的切线方程为1y x =-，即10x y --=.（2）()'2g x ax b =-，由题意(2)0(2)2g g =⎧⎨=-'⎩，即40422a b a b -=⎧⎨-=-⎩，解得122a b ⎧=⎪⎨⎪=⎩，经检验，1,22a b ==满足题意，所以()2122g x x x =-.18．（1）证明：连接BD ，则O 为BD 中点， 又E 为PD 中点，∴OE //PB .∵PB ⊂平面PAB ，OE ⊄平面PAB ， ∴OE //平面PAB（2）以A 为原点建立空间直角坐标系， 如图，则(0,0,1),(1,2,0),(0,2,0)P C D ，110,1,,,1,022E O ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ ∴11(1,2,1),,0,22PC OE ⎛⎫=-=- ⎪⎝⎭，∴3cos ,162PC OE ==⋅即异面直线PC 与OE 319．（1）把()1,2代入抛物线方程解得2P = ∴E 的方程为24y x =.（2）法一：由（1）得抛物线E 的方程为24y x =,焦点()1,0F设A ,B 两点的坐标分别为()11,Ax y ,()22,B x y ,代入抛物线可得则21122244y x y x ⎧=⎨=⎩,两式相减,整理得()211221214y y x x x x y y -=≠-+ ∵线段AB 中点的纵坐标为1- ∴直线l 的斜率()2144212AB k y y ===-+-⨯直线l 的方程为()021y x -=--即220x y +-=法二：由（1）得抛物线E 的方程为24y x =,焦点()1,0F设直线l 的方程为1x my =+ 由241y x x my ⎧=⎨=+⎩消去x ,得2440y my --=设A ,B 两点的坐标分别为()11,Ax y ,()22,B x y ,∵线段AB 中点的纵坐标为1- ∴()124122m y y --+==- 解得12m =-直线l 的方程为112x y =-+即220x y +-= 20．（1）设AC 与BD 相交于点O ，连接FO ，∵四边形ABCD 为菱形，∴AC BD ⊥，且O 为AC 中点，∵FA FC =，∴AC FO ⊥，又FO BD O ⋂=，∴AC ⊥平面BDEF （2）连接DF ，∵四边形BDEF 为菱形，且60DBF ∠=︒，∴DBF 为等边三角形，∵O 为BD 中点，∴FO BD ⊥，又AC FO ⊥， ∴FO ⊥平面ABCD .∵OA ，OB ，OF 两两垂直，∴建立空间直角坐标系O xyz -，如图所示，设2AB =，四边形ABCD 为菱形，60DAB ∠=︒，∴2BD =，23AC =∵DBF 为等边三角形， 3.OF =∴3,0,0)A ，()0,1,0B ，()0,1,0D -，3)F ∵DB EF =，//DB EF ∴(0,3)E -(3,1,0AD =--，(3,0,3)AF =-，(0,2,0)EF =.设平面AEF 的法向量为(,,)n x y z =，则33020AF n x z EF n y ⎧⋅=-+=⎪⎨⋅==⎪⎩，取1x =，得()1,0,1n =.设直线AD 与平面AEF 所成角为θ， 则||6sin cos ,4||||AD n AD n AD n θ⋅=<>==⋅. 21．（1）()ln f x x x =-，1()1f x x'=-，(0)x ∈+∞，， 由()0f x '>，得1x >，由()0f x '<，得01x <<， 所以()f x 在(01)，上单调递减，在(1)+∞，上单调递增， 所以()f x 有极小值(1)1f =，无极大值.（2）()ln (1)f x x x m x m =-≥-+即ln (1)0x m x --≤.记()ln (1)h x x m x =--，则()0≤h x 对任意(0)x ∈+∞，恒成立， 求导得1()h x m x'=-（0x >）， 若0m ≤，则()0h x '>，得()h x 在(0)+∞，上单调递增，又(1)0h =， 故当1x >时，()0h x >，不合题意； 若0m >，由()h x '0>得10x m <<，由()h x '0<得1x m>， 所以()h x 在10m ⎛⎫ ⎪⎝⎭，上单调递增，在1m ⎛⎫+∞ ⎪⎝⎭，单调递减. 依题意有max 1()ln 10()1h x h m m f m m ⎛⎫==--+⇔ ⎪⎝⎭≤≤，22．解：（1）由题可知，椭圆C的离心率为2，且椭圆过点)M ，则222222211c e a a b a b c ⎧==⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得：24a =，222c b ==， 故椭圆C 的方程为22142x y +=；（2）过点(1,0)作斜率为2直线l ，∴直线:22l y x =-，联立2214222x y y x ⎧+=⎪⎨⎪=-⎩，整理得：291640x x -+=， 设1(A x ，1)y ，2(B x ，2)y ，则12169x x +=，1249x x =， 2221212216164||()4535999AB x x x x ∴=+-=-=； （3）由于直线l 过点()1,0直线l ，设1(A x ，1)y ，2(B x ，2)y ， 当直线l 的斜率不存在时，直线l x ⊥轴，此时将1x =代入22142x y +=，解得：y =， 即A ，B的坐标分别为1,,1,22⎛⎛⎫- ⎪ ⎪⎝⎭⎝⎭，则OAB的面积为：12111222S y y =-⨯==； 当直线l 的斜率存在，且不为0时，可设直线l 的方程为：1x my =+，联立221421x y x my ⎧+=⎪⎨⎪=+⎩，整理得：()222230m y my ++-=， 则12122223,11m y y y y m m --+==++， 而OAB 的面积为：12112S y y =-⨯=即S ==12===令t =>2246t m =+，得 2264t m -=，所以(22244262224t t S t t m t t t ====>-++++， 由于t >23t t +>=则42S t t t=<=>+ 所以综上得：S ≤，所以OAB。

武威六中2020-2021学年度第一学期第一次学段考试高二数学（理）试卷一、选择题（每小题5分，共60分，只有一个正确选项）1．已知ABC ∆的顶点,B C 在椭圆2213x y +=上，顶点A 是椭圆的一个焦点，且椭圆的另一个焦点在BC 边上，则ABC ∆的周长是（ ）A ．B ．6C ．D ．122．双曲线2212516x y -=的一个焦点坐标为（ ）A.(3,0)B. (0,4)-C. (D. 3．抛物线21y x a=的准线方程是1=y ，则a 的值是（ ） A.41 B. 41- C. 4 D.4- 4．已知中心在原点的双曲线C 的一个顶点为(0,2)-，虚轴长为2．则双曲线C 的方程为( )A. 2214x y -= B ．22144y x -= C ．2214y x -= D ．2214y x -=5．已知椭圆221102x y m m +=--，长轴在y 轴上. 若焦距为，则m 等于（ ） A.4 B.5 C.7 D.86．设椭圆22221(00)x y m n m n +=>>，的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为（ ）A ．2211216x y += B ．2211612x y += C ．2214864x y += D ．2216448x y += 7．相距1千米的甲、乙两地，听到炮弹爆炸的时间相差2秒，则炮弹爆炸点的轨迹可能是（ ）A ．双曲线的一支B ．双曲线C ．椭圆D ．抛物线8．过椭圆)0(12222>>=+b a b y a x 的左焦点1F 做x 轴的垂线交椭圆于点P ,2F 为右焦点,若1230F F P ∠=,则椭圆的离心率为（ ）A.22 B.31C.21D.33 9．若点(2,0)P 到双曲线22221x y a b-=，则双曲线的离心率为（ ）C.D.10．P 为椭圆14522=+y x 上的点，21,F F 是两焦点，若1260F PF ∠=，则21PF F ∆的面积是（ ）B.C.D. 11．椭圆221ax by +=与直线12y x =-交于A 、B 两点，过原点与线段AB 中点的直线的斜率为，则ab的值为（ ）C.12．抛物线22y x =上的点到直线50x +=距离的最小值是 （ ）A.3B.74 C.85 D.43二、填空题（每小题5分，共20分）13．若00(,)P x y 是双曲线22124x y -=左支上一点，则0x 的取值范围是 ； 14．抛物线C 的顶点为坐标原点，对称轴为y ，且焦点在直线2350x y --=上．则抛物线C的方程为 ；15．直线l 过抛物线2: 2C y x =的焦点F ，且与抛物线C 交于,A B 两点（点A 在x 轴的上方），若||2AF =，则||BF = ；16．椭圆2222:1(0)x y E a b a b+=>>的左、右焦点分别为12,F F P 、为椭圆E 上任一点，且12PF PF 的最大值的取值范围是22[2,4]c c ，其中c =则椭圆E 的离心率e 的取值范围是_________.三、解答题（共70分，写出必要的步骤）17．（本小题共10分）如图所示，在ABC ∆中，||6AB =，且ABC ∆的周长为20．建立适当的坐标系，求顶点C 的轨迹方程．18．（本小题共12分）已知点,A B 的坐标分别是(2,0),(2,0)-，直线AP 与BP 相交于点P ，且它们的斜率之积为(0)m m ≠，求点P 的轨迹方程，并说明轨迹是什么图形．19．（本小题共12分）点P 是椭圆2222: 1(0)x y C a b a b+=>>一点，F 为椭圆C 的一个焦点，||PF11．（1）求椭圆C 的方程；（2）直线y x m =+被椭圆C，求m 的值．B20．（本小题共12分）双曲线C 与双曲线2212y x -=有共同的渐近线，且过点． （1）求双曲线C 的方程；（2）若直线:1l y kx =+与双曲线C 左支交于,A B 两点，求k 的取值范围；21．（本小题共12分）已知F 为抛物线2:2(0)C y px p =>的焦点，过F 垂直于x 轴的直线被C 截得的弦的长度为4． （1）求抛物线C 的方程；（2）过点(,0)m ，且斜率为1的直线被抛物线C 截得的弦为AB ，若点F 在以AB 为直径的圆内，求m 的范围．22．（本小题共12分）已知椭圆22221(0)x y a b a b+=>>的左、右焦点为别为1F 、2F ，且过点(1,)2和22. （1）求椭圆的标准方程；（2）如图，点A 为椭圆上一动点（非长轴端点），2AF 的延长线与椭圆交于点B ，AO 的延长线与椭圆交于点C ，求ABC ∆面积的最大值．x高二数学（理）答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CCDDCB BDAACB二、填空题13. (,2)-∞- 14. y x 3202-= 15. 23 16. 53,⎡⎤⎢⎥⎣⎦三、解答题17.解：以AB 边所在的直线为x 轴，AB 的垂直平分线为y 轴，建立平面直角坐标系，如图所示，则A (－3，0)，B (3，0)．因为||6AB =，且ABC ∆的周长为20，所以|AC |+|BC |＝20-6=14>6. （5分）由椭圆的定义知，点C 的轨迹是以A (－3，0)，B (3，0)为焦点，长轴长为14的椭圆(除去与x 轴的交点)．所以a ＝7，c ＝3，b 2＝a 2－c 2＝40即所求轨迹方程为)x (y x 71404922±≠=+. （10分） 18.解：设动点M （x,y ）,m k k BM AM =⋅ 则m x y x y =-⋅+22，整理得m mx y 422-=-， 即221(2)4-4x y x m+=≠±. （3分） (1)当m ＝-1时，422=+x y ，表示圆心在原点，半径为2的圆； （6分）(2)当-4m>0即m<0且1m ≠-时，方程221(2)4-4x y x m+=≠±，表示椭圆（除去与x 轴两个交点）； （9分）(3)当-4m ＜0即m ＞0时，方程为221(2)4-4x y x m+=≠±，表示的双曲线（除去与x 轴两个交点）. （12分） 19.解：（1）由题意可知121212==+=+-=-c ,a c a ,c a ，解得，所以椭圆方程为2212x y +=. （4分） （2）设直线l 与曲线C 的交点M (x 1，y 1)，N (x 2，y 2)，联立⎪⎩⎪⎨⎧=++=1222y x m x y 得0224322=-++m mx x ,33-022121622<<>--=∆m )m (m 即,又32234-22121-=⋅=+m x x ,m x x ， （8分） |MN |＝1＋k2·（x 1＋x 2）2－4x 1·x 2＝423， 整理得0882=-m ∴m ＝±1，符合题意.综上，m ＝±1. （12分）20.解：（1）设双曲线C 的方程为222y x λ-=，把点代入可得1λ=-，所以双曲线C 的方程为2212y x -=。

甘肃省武威第六中学2021学年下学期高二年级第二次学段考试（期末）数学试卷（理科）一、单选题1．已知集合{}1,1,2A =-，集合{}1,2,3,4B =，则集合A B =（ ）A ．{}1,2B ．{}1,1,2-C ．{}1,2,3D ．{}1,1,2,3,4-2．已知复数2332iz i+=-，则z =（ ）A ．1i +B ．iC ．i -D ．1i -3．某天的值日工作由4名同学负责，且其中1人负责清理讲台，另1人负责扫地，其余2人负责拖地，则不同的分工共有（ ）A ．6种B ．12种C ．18种D ．24种4．如图所示的是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，甲、乙两人这几场比赛得分的平均数分别为甲x ，乙x ，标准差分别为甲s ，乙s ，则有（ ）A ．x x >甲乙，s s >乙甲B ．x x <甲乙，s s >乙甲C ．x x >甲乙，s s <乙甲D ．x x <甲乙，s s <乙甲5．《周髀算经》中提出了“方属地，圆属天”，也就是人们常说的“天圆地方”．我国古代铜钱的铸造也蕴含了这种“外圆内方”“天地合一”的哲学思想．现将铜钱抽象成如图所示的图形，其中圆的半径为r ，正方形的边长为a （0＜a ＜r ），若在圆内随机取点，得到点取自阴影部分的概率是() 1a p r +()221a p r +() 1a p r-()221a p r-()P B A 131181619()()5212ax x +-2x9.49.1y x =+a()()()()()22=n ad bc K a b c d a c b d -++++n a b c d =+++52ξE ξ=3721854()ln (R)f x x a x a a =-+∈(,)e +∞()2,e +∞()23,e e ()22,2e e )0(sin π≤≤=x x y 12y =m 55432543210(1)mx a x a x a x a x a x a -=+++++1234533a a a a a ++++=m =110120X <<()2~,X N μσ()0.6827P X μσμσ-<<+=(22)0.9545P X μσμσ-<<+=(33)0.9973P X μσμσ-<<+=2()(3)x f x x e =-()f x ()f x ()f x b =36b e ->()f x b =306b e -<<Ccos sin ρθθ=+l 20x y -+=C l C l []130,140[]90,140()32392f x x x x =-++-()y f x =()()0,0f ()f x 1223X X ()ln f x x ax =-()f x 1a ()()()2xh x x e f x =-+1a ≥()h x b ≤1,13x ⎛⎤∈ ⎥⎝⎦b xOy l 252x m t y t⎧=-⎪⎨=+⎪⎩t O x C 25sin ,l ρθ=C 2m C l A B 、P (,5)m 0m >PA PB+0x =1x =值．【详解】在55432543210(1)mx a x a x a x a x a x a -=+++++中，取0x =，得01a -=，取1x =，得5543210(1)m a a a a a a -=+++++， 所以512345(1)133a a a a a m ++++=-+=，所以5(1)32m -=，解得3m = 故答案为：3 【点睛】本题主要考查二项式定理的应用，对x 恰当的赋值是解题的关键，属于基础题 15．40000 【解析】 【分析】首先根据条件判断100,10μσ==，可知()()1101202P X P x μσμσ<<=+<<+，根据条件求得概率，最后再计算样本总量 【详解】()100,100XN可知100,10μσ==()()1101202P X P x μσμσ<<=+<<+()()222P x P X μσμσμσμσ-<<+--<<+=0.95450.68270.13592-==,又5436400000.1359=（件） 故填：40000 【点睛】本题考查了正态分布应用的实际问题，计算正态分布下的概率时，需充分应用曲线关于x μ=对称，对称轴两侧的概率均为0.5 16．②④ 【解析】2()(23)013x f x x x e x =+-=∴=-'或所以当3x <- 时，3()0,()(0,6)f x f x e -∈'> ；当31x -<< 时，3()0,()(2,6)f x f x e e -<∈-' ；当1x > 时，()0,()(2,)f x f x e ∈-'>+∞ ；因此()f x 有极小值()1f ，也有最小值()1f ，有极大值()3f -，但无最大值；若方程()f x b =恰有一个实数根，则36b e ->或2b e =-; 若方程()f x b =恰有三个不同实数根，则306b e -<<,即正确结论的序号为②④ 点睛：对于方程解的个数或函数零点个数问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等．17．（Ⅰ）C :220x y x y +--=，l :cos sin 20ρθρθ-+=；（Ⅱ）2【解析】 【分析】（Ⅰ）根据222cos ,sin ,x y x y ρθρθρ==+=进行直角坐标与极坐标互化，（Ⅱ）根据圆心到直线距离减去半径得结果 【详解】（Ⅰ）圆C ：cos sin ρθθ=+，即2cos sin ρρθρθ=+，圆C 的直角坐标方程为：22x y x y +=+，即220x y x y +--=； 直线l ：20x y -+=，则直线l 的极坐标方程为cos sin 20ρθρθ-+=（Ⅱ）由圆C 的直角坐标方程为220x y x y +--=可知圆心C 坐标为11,22⎛⎫ ⎪⎝⎭，半径为2，因为圆心C 到直=C 上的点到直线l22= 【点睛】本题考查直角坐标与极坐标互化以及直线与圆位置关系，考查基本分析求解能力，属中档题 18．（1）40；（2）众数115、中位数113，平均数113 【解析】 【分析】（1）先求得成绩在[]130,140内的频率，结合[]130,140分数段的人数即可求得成绩在[]90,140分数段的学生人数；（2）根据频率分布直方图中最高矩形，即可得众数；从左至右，将小矩形面积求和，至面积和为时，对应底边的数值即为中位数；将各小矩形面积乘以对应底边的中点值，求和即为平均数的估计值（1）∵[]130,140分数段的频率为0.005100.05⨯=， 又[]130,140分数段的人数为2，∴[]90,140分数段的参赛学生人数为20.0540÷=（2）根据频率分布直方图，最高小矩形底面中点值为115，所以90分以上（含90分）的学生成绩的众数的估计值为115，从左依次计算各小矩形的面积为0.10.250.450.5++>，因而中位数的估计值为0.50.10.25340101101130.453--⨯+=≈，平均数的估计值为950.11050.251150.451250.151350.05113⨯+⨯+⨯+⨯+⨯= 【点睛】本题考查了频率分布直方图的简单应用，由频率分布直方图估计众数、中位数与平均数，属于基础题 19．（1）920x y --=；（2）(),1-∞-，()3,+∞ 【解析】 【分析】（1）利用导数的几何意义可求得切线斜率，进而得到切线方程； （2）根据导函数的正负即可确定所求的单调区间 【详解】（1）由题意得：()()()()22369323331f x x x x x x x =-++=---=--+'，()09f '∴=，又()02f =-，()y f x ∴=在()()0,0f 处的切线方程为()290y x +=-，即920x y --=（2）由（1）知：()()()331f x x x '=--+，∴当(),1x ∈-∞-()3,⋃+∞时，()0f x '<；当()1,3x ∈-时，()0f x '>；()f x ∴的单调递减区间为(),1-∞-，()3,+∞【点睛】本题考查利用导数的几何意义求解在某一点处的切线方程、利用导数求解函数的单调区间的问题，属于导数部分知识的基础应用 20．（1）548（2）5716【分析】 【详解】（1）若该生被录取，则前四项最多有一项不合格，并且第五项必须合格 记A={前四项均合格}，B={前四项中仅有一项不合格} 则4121()()(1)2348P A =-=⋅ 3141121()1122312P B C ⎛⎫⎛⎫=⨯⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭又A 、B 互斥，故所求概率为4115()(128)48p P A P B =+=+=， 所以该生被录取的概率是548； （2）该生参加考试的项数X 可以是2，3，4，5111(2)224P X ==⨯=，121111(3)(1)2224P X C ==-⨯⨯= 2231113(4)(1)22216P X C ==-⨯⨯=，1135(5)1441616P X ==---=113557()234544161616E X =⨯+⨯+⨯+⨯=考点：本题考查了随机变量的概率与期望点评：本题考查了随机事件的概率及随机变量的分布列、期望的综合运用，考查了学生的计算能力及解决实际问题的能力，掌握求分布列的步骤及期望公式是解决此类问题的关键 21．（1）2a e -=；（2）3-． 【解析】 【分析】（1）先对函数()y f x =求导，对实数a 分0a >和0a ≤两种情况讨论，利用导数分析函数()y f x =在定义域上的单调性，进而可求最大值，由此可求出实数a 的值；（2）由已知整理可得，()2ln xb x e x ax ≥-+-对任意的1,13x ⎛⎤∈ ⎥⎝⎦恒成立，结合1a ≥，0x >，可知()()2ln 2ln x x x e x ax x e x x -+-≤-+-，故只需()2ln xb x ex x ≥-+-对任意的1,13x ⎛⎤∈ ⎥⎝⎦恒成立，构造函数()()2ln x g x x e x x =-+-，利用导数求出函数()y g x =的最大值的取值范围，由此可求得满足条件的实数b的最小整数值． 【详解】（1）由题意，函数()y f x =的定义域为()0,∞+，()1f x a x'=-， 当0a ≤时，()10f x a x'=->，函数()y f x =在区间()0,∞+上单调递增， 此时，函数()y f x =在定义域上无最大值；当0a >时，令()10f x a x'=-=，得1x a=，由()0f x '>，得10,x a ⎛⎫∈ ⎪⎝⎭，由()0f x '<，得1,x a ⎛⎫∈+∞ ⎪⎝⎭，此时，函数()y f x =的单调递增区间为10,a ⎛⎫ ⎪⎝⎭，单调减区间为1,a ⎛⎫+∞⎪⎝⎭． 所以函数()()2max 111ln 11f x f x f a a a e ⎛⎫===-=⇒= ⎪⎝⎭极大值， 即2a e -=为所求；（2）由()()2ln xh x x e x ax =-+-，因为()h x b ≤对任意的1,13x ⎛⎫∈ ⎪⎝⎭恒成立，即()2ln xb x e x ax ≥-+-，当1a ≥时，对任意的1,13x ⎛⎫∈ ⎪⎝⎭恒成立，1a ≥，0x >，()()2ln 2ln x x x e x ax x e x x ∴-+-≤-+-，只需()2ln xb x e x x ≥-+-对任意的1,13x ⎛⎫∈ ⎪⎝⎭恒成立即可．构造函数()()2ln xg x x e x x =-+-，()()()11111x x g x x e x e x x ⎛⎫'=-+-=-- ⎪⎝⎭，1,13x ⎛⎫∈ ⎪⎝⎭，10x ∴-<，且()1x t x e x =-单调递增，121202t e ⎛⎫=-< ⎪⎝⎭，()110t e =->，∴一定存在唯一的01,13x ⎛⎫∈ ⎪⎝⎭，使得()00t x =， 即01x ex =，00ln x x =-， 且当013x x <<时，()0t x <，即()0g x '>；当01x x <<时，()0t x >，即()0g x '< 所以，函数()y g x =在区间01,3x ⎛⎫⎪⎝⎭上单调递增，在区间()0,1x 上单调递减，()()()()000000max 012ln 124,3x g x g x x e x x x x ⎛⎫∴==-+-=-+∈-- ⎪⎝⎭，因此，b 的最小整数值为3- 【点睛】本题考查了利用导数求解函数的最值，同时也考查了利用导数求解函数不等式恒成立问题，考查了推理能力与计算能力，属于中档题．22．（Ⅰ）33m m ==-或；（Ⅱ）【分析】（Ⅰ）先将圆C 的方程化成直角坐标方程，直线l 化成普通方程，再由圆心到直线的距离以及勾股定理列式可得；（Ⅱ）联立直线l 与圆C 的方程，根据韦达定理以及参数的几何意义可得． 【详解】（Ⅰ）由ρθ=得220,x y +-=即(225x y += 直线的普通方程为0xy m +--=，被圆C=解得33m m ==-或（Ⅱ）法1：当3m =时，将l的参数方程代入圆C 的直角坐标方程得，())2235-+=，即2220t -+=，由于(24420∆=-⨯=>，故可设12t t ，是上述方程的两实根，所以121221t t t t⎧+=⎪⎨⎪=⎩，又直线l 过点(P ，故由上式及t 的几何意义得，PA PB += 122(|t |+|t |)= 122(t +t )=法2：当3m =时点(3P，易知点P 在直线l 上 又2235+>，所以点P 在圆外联立(22530x y x y ⎧+=⎪⎨⎪+--=⎩消去y 得，2320x x -+=不妨设((2A B ，、，所以PA PB +==【点睛】本题考查参数方程，极坐标方程与直角坐标方程之间的互化，考查直线参数方程中参数t 的几何意义的应用，属于基础题。

甘肃省武威第六中学2020-2021学年高二下学期第二次学段考试（期末）数学（文）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合M ＝{x|(x －1)2＜4，x ∈R}，N ＝{－1，0，1，2，3}，则M∩N ＝（ ） A ．{0，1，2} B ．{－1，0，1，2} C ．{－1，0，2，3} D ．{0，1，2，3} 2．若命题p 的逆命题是q ，否命题是r ，则q 是r 的（ ）A ．逆命题B ．否命题C ．逆否命题D ．以上都不正确 3．若4sin 5α，且α为锐角，则sin 2α的值等于（ ）. A ．1225 B ．2425 C ．1225- D ．2425- 4．“a 、b 、c成等比数列”是“b =） A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件5．函数sin cos y x x =⋅的最小正周期和最大值分别为（ ）A ．π，1B ．π，12C ．2π，1D ．2π，12 6．已知5log 2a =，0.5log 0.2b =，0.20.5c =，则,,a b c 的大小关系为（ ） A ．a c b <<B ．a b c <<C ．b c a <<D ．c a b << 7．函数()21,11,1x x x f x x x⎧-+<⎪=⎨>⎪⎩的值域为（ ） A ．3,4⎡⎫+∞⎪⎢⎣⎭ B ．()0,1 C ．3,14⎡⎫⎪⎢⎣⎭ D ．()0,∞+8．函数()22x xx f x -=+的大致图象为（ ）A ．B ．C ．D ．9．若函数()f x ax b =+的零点是2（0a ≠），则函数2()g x ax bx =+的零点是（ ）A ．2B ．2和0C ．0D ．2-和010．已知全集U =R ，设函数()lg 1y x =-的定义域为集合A ，函数y 的值域为集合B ，则()U AC B =（ ） A ．[)1,3 B ．[]1,3C ．()1,3D ．(]1,3 11．函数()f x 定义在0,2π⎛⎫ ⎪⎝⎭上，()f x '是它的导函数，且()()tan x f x f x '⋅>在定义域内恒成立，则（ ）A ．43f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B 63f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭C ．()cos116f f π⎛⎫⋅> ⎪⎝⎭D 46ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭12．已知()f x 是定义域为(),-∞+∞的奇函数，满足()()2f x f x =-.若()11f =，则()()()()1232019f f f f +++⋅⋅⋅+=（ ）A ．-2019B ．1C ．0D ．2019二、填空题132032(3)log 6427π+-+-=__________. 14．已知()2log ,0,21,0,x x x f x x ->⎧=⎨-+<⎩则方程()3f x =的解是x =______. 15．函数2()34f x x mx =-+在[5,)-+∞上是增函数，在(,5]-∞-上是减函数，则(1)f -=_________．16．若()323ln 442f x m x x x x =-+-+在()2,+∞上单调递减，则实数m 取值范围__________.三、解答题17．已知:p 22a -<<，q ：关于x 的方程20x x a -+=有实数根.（1）若q 为真命题，求实数a 的取值范围；（2）若p q ∨为真命题，q ⌝为真命题，求实数a 的取值范围.18．已知()()()()3sin cos 2cos 2cos sin 2f ππαπαααπαπα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭. (1)化简()f α；(2)若α是第三象限角，且()1sin 5απ-=，求()f α的值. 19．()()()222f x x m x m m R =+--∈(1)已知()f x 在[]2,4上是单调函数,求m 的取值范围；(2)求()0f x <的解集.20．已知函数32111()2322f x x x x =---. （1）求函数()f x 的单调区间；（2）当[2,4]x ∈-时，求函数()f x 的最大值.21．已知函数2()(1)1()x f x mx x e m R =+-+∈.（1）当0m ≥时，讨论函数()f x 的单调性；（2）证明：当1,13x ⎛⎫∈ ⎪⎝⎭时，23()f x mx x >+. 22．已知曲线4cos :3sin x C y θθ=⎧⎨=⎩（θ为参数）． （1）将C 的方程化为普通方程；（2）若点(,)P x y 是曲线C 上的动点，求2x y +的取值范围．参考答案1．A【解析】试题分析：求出集合M 中不等式的解集，确定出M ，找出M 与N 的公共元素，即可确定出两集合的交集．解：由（x ﹣1）2＜4，解得：﹣1＜x ＜3，即M={x|﹣1＜x ＜3}，∵N={﹣1，0，1，2，3}，∴M∩N={0，1，2}．故选A点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．C【分析】首先设原命题p 为：若m 则n ，分别求出逆命题是q 和否命题是r ，再判断即可得到答案.【详解】设原命题p 为：若m 则n ，则逆命题q 为：若n 则m ，否命题r 为：若m ⌝则n ⌝. 则q 是r 的逆否命题.故选：C【点睛】本题主要考查四种命题，熟练掌握四种命题的关系为解题的关键，属于简单题.3．B【分析】根据二倍角的正弦公式计算即可.【详解】 4sin 5α=,α为锐角, 3cos 5α∴=, 4324sin 22sin cos 25525ααα∴==⨯⨯=, 故选：B【点睛】本题主要考查了同角三角函数的基本关系，二倍角的正弦公式，属于容易题.4．D【分析】利用充分条件和必要条件的定义结合等比中项的定义判断即可.【详解】充分性：若a 、b 、c 成等比数列，则2b ac =且0ac >，则b =必要性：若b =0a b c ===，则a 、b 、c 不成等比数列，即必要性不成立.因此，“a 、b 、c 成等比数列”是“b =. 故选：D.【点睛】本题考查充分条件、必要条件的判断，同时也考查了等比中项定义的应用，考查计算能力与推理能力，属于基础题.5．B【分析】 利用倍角公式可得1sin cos sin 22y x x x =⋅=，进而求得其最小正周期和最大值. 【详解】 解：根据倍角公式可知1sin cos sin 22y x x x =⋅=， 函数sin cos y x x =⋅的最小正周期22T ππ==， 1sin 21x -≤≤，∴111sin 2222x -≤≤， ∴sin cos y x x =⋅的最大值为12. 故选：B.【点睛】本题考查三角函数恒等变换的应用，着重考查倍角公式，考查三角函数的周期性及其求法，属于基础题.6．A【分析】利用10,,12等中间值区分各个数值的大小．【详解】551log 2log 2a =<<， 0.50.5log 0.2log 0.252b =>=，10.200.50.50.5<<，故112c <<， 所以a c b <<．故选A ．【点睛】本题考查大小比较问题，关键选择中间量和函数的单调性进行比较．7．D【分析】分别求出当1,1x x <>时的值域,再取并集即可.【详解】当1x <时,2213()1()24f x x x x =-+=-+,故3(),,(1)4f x x ⎡⎫∈+∞<⎪⎢⎣⎭. 当1x >时,1()(0,1)f x x =∈,故()21,11,1x x x f x x x⎧-+<⎪=⎨>⎪⎩的值域为()0,∞+. 故选D.【点睛】分段函数的值域只需每段函数单独求解值域再求并集即可.8．B【分析】根据函数为奇函数排除C ，取特殊值排除AD 得到答案.【详解】 当()22x xx f x -=+，()()22x x x f x f x ---==-+，函数为奇函数，排除C ；2221(2)22242f -=<=+，排除A ； 3324(3)22536f -==+，4464(4)224257f -==+，故()()34f f >，排除D. 故选：B.【点睛】本题考查了函数图象的识别，意在考查学生的计算能力和识图能力，取特殊值排除是解题的关键.9．B【分析】首先根据()f x 的零点是2求得,a b 的关系式，对()g x 因式分解，由此求得()g x 的零点.【详解】由条件知(2)0f =，∴2b a =-，∴2()(2)g x ax bx ax x =+=-的零点为0和2.故选B .【点睛】本小题主要考查函数零点的知识运用，属于基础题.10．C【解析】∵全集U=R ，设函数y=lg （x ﹣1）的定义域为集合A ，∴A={x|x ﹣1＞0}={x|x ＞1}，∵函数y =的值域为集合B ，∴B={y|y =，∴C U B={y|y ＜3}，∴A∩（∁U B ）=（{x|1＜x ＜3}=（1，3）．故选C ．11．D【分析】 构造函数()cos (),0,2g x x f x x π⎛⎫=⋅∈ ⎪⎝⎭，利用所给不等式判断()'g x 的符号推出()g x 的单调性，利用()g x 的单调性即可比较函数值的大小.【详解】 因为0,2x π⎛⎫∈ ⎪⎝⎭，所以sin 0cos 0x x >>，， 由()()tan x f x f x '⋅>可得()cos ()sin f x x f x x '<，即()cos ()sin 0f x x f x x '-<， 令()cos (),0,2g x x f x x π⎛⎫=⋅∈ ⎪⎝⎭，则()()cos ()sin 0g x f x x f x x ''=-<， 所以函数()g x 在0,2π⎛⎫ ⎪⎝⎭上为减函数，则(1)643g g g g πππ⎛⎫⎛⎫⎛⎫>>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 则cos cos cos(1)(1)cos 664433f f f f ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫>>> ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，2cos(1)(1)643f f πππ⎛⎫⎛⎫⎛⎫>>>⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选：D【点睛】 本题考查利用导数研究函数的单调性、函数单调性的应用，属于中档题.12．C【分析】推导出函数()f x 为周期为4的周期函数，()11f =，(2)(02)(0)0,(3)(12)(1) 1.(4)(0)0,f f f f f f f f =+=-==+=-=-== 由此能求出()()()()1232019.f f f f +++⋅⋅⋅+【详解】()f x 是定义域为(),-∞+∞的奇函数，满足()()2f x f x =-，则有()()2f x f x -=+ ，又由函数()f x 为奇函数，则()()f x f x -=- ，则有(2)().f x f x +=- ∴ (4)(2)f x f x +=-+ ∴ (4)().f x f x +=则函数()f x 是周期为4的周期函数，()11f ∴=，(2)(02)(0)0,(3)(12)(1) 1.(4)(0)0,f f f f f f f f =+=-==+=-=-==∴()()()()[]1232019504(1)(2)(3)(4)(1)(2)(3) 50401010.f f f ff f f f f f f+++⋅⋅⋅+=⨯++++++=⨯++-=【点睛】本题考查了函数的奇偶性，周期性．通过函数的奇偶性和周期性推导出函数的周期是关键．13．1【分析】根据指数幂运算及对数的性质,化简即可求解.【详解】根据指数幂运算及对数的性质,化简可得2032(3)log6427π-+-()2633231log23=-++-31691=++-=.故答案为:1【点睛】本题考查了指数幂运算及对数的性质应用,属于基础题.14．8【分析】采用分类讨论进行求解，结合对数方程以及指数方程的解法，可得结果.【详解】由题可知：①28log3xxx>⎧⇒=⎨=⎩，②213xxx-<⎧⇒∈∅⎨-+=⎩故方程()3f x=的解是8x=故答案为：8【点睛】本题考查根据分段函数解析式，给出函数值求解，关键在于分类讨论方法的使用，审清题意，细心计算，属基础题.15．23-【分析】根据二次函数单调性确定m 的值，代入函数求解函数值.【详解】函数2()34f x x mx =-+在[5,)-+∞上是增函数，在(,5]-∞-上是减函数， 所以5,306m m =-=-，2()3304f x x x =++， (1)330423f -=-+=-.故答案为：23-【点睛】此题考查根据函数单调性求参数的取值，根据函数解析式求解函数值，属于简单题目. 16．(],20-∞【分析】由题可知，求导()2334m f x x x x'=-+-，由于()f x 在()2,+∞上单调递减，则转化为()0f x '≤在()2,+∞上恒成立，分离参数法，转化为32334m x x x ≤-+在()2,+∞上恒成立，构造新函数()()323342g x x x x x =-+>，利用导数研究函数的单调性和最值，求出()min g x 即可得出m 取值范围.【详解】解：()323ln 442f x m x x x x =-+-+()0x >， ()2334m f x x x x'∴=-+-， 由于()f x 在()2,+∞上单调递减，即()0f x '≤在()2,+∞上恒成立， 即23340m x x x-+-≤在()2,+∞上恒成立， 则32334m x x x ≤-+在()2,+∞上恒成立，即()min m g x ≤在()2,+∞上恒成立，设()()323342g x x x x x =-+>，()2964g x x x '=-+，知364940∆=-⨯⨯<，()2,x ∴∈+∞时，()0g x '>，()g x 单调递增，()()32min 232324220m g x g ∴≤==⨯-⨯+⨯=，20m ∴≤，即实数m 取值范围为(],20-∞.故答案为：(],20-∞.【点睛】本题考查利用导数研究函数的单调性求参数范围，以及利用函数解决恒成立问题，考查转化思想和计算能力.17．（1）14a ≤；（2）124a << 【分析】（1）关于x 的方程x 2﹣x+a=0有实数根，则△=1﹣4a≥0，解得a 的范围．（2）由题意得p 为真命题，q 为假命题求解即可.【详解】（1）方程20x x a -+=有实数根，得：:140q a ∆=-≥得14a ≤； （2）p q ∨为真命题，q ⌝为真命题∴ p 为真命题，q 为假命题，即2214a a -<<⎧⎪⎨>⎪⎩得124a <<. 【点睛】本题考查了一元二次方程的实数根与判别式的关系、复合命题真假的判断方法，考查了推理能力，属于基础题．18．(1)()cos f αα=-;(2)5. 【分析】(1)根据诱导公式直接化简即可;(2)由()1sin 5απ-=,可以利用诱导公式计算出sin α,再根据角所在象限确定cos α,进而得出结论.【详解】(1)根据诱导公式()()()()3sin cos 2cos 2cos sin 2f ππαπαααπαπα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭()sin cos sin sin sin ααααα⋅⋅-=⋅ cos α=-,所以()cos f αα=-;(2)由诱导公式可知()sin sin απα-=-,即1sin 5α=-, 又α是第三象限角,所以cos 5α==-, 所以()=cos f αα-=【点睛】 本题主要考查诱导公式的运用,属于基础题.使用诱导公式时,常利用口诀“奇变偶不变,符号看象限”进行记忆.19．(1) 6m ≤-或2m ≥-；(2) 当2m =-时,不等式()0f x <的解集为空集； 当2m >-时, 不等式()0f x <的解集为{}2x m x -<<；当2m <-时, 不等式()0f x <的解集为{}2x x m <<-.【分析】(1)求出函数的对称轴,然后根据二次函数的单调性,由题意分类讨论即可求m 的取值范围；(2)根据一元二次方程根之间的大小关系进行分类讨论求出()0f x <的解集.【详解】(1)函数 ()()()222f x x m x m m R =+--∈的对称轴为：22m x -=因为()f x 在[]2,4上是单调函数,所以有：242m -≥或222m -≤,解得 6m ≤-或2m ≥-；(2)方程()2220x m x m +--=的两个根为：2,m -. 当2m =-时,不等式()0f x <的解集为空集；当2m >-时, 不等式()0f x <的解集为{}2x m x -<<；当2m <-时, 不等式()0f x <的解集为{}2x x m <<-.【点睛】本题考查了已知函数单调性求参数问题,考查了求解一元二次不等式的解集,考查了分类讨论思想.20．（1）()f x 的单调增区间为(),1-∞-，()2,+∞；单调减区间为()1,2-（2）()max 296f x =【分析】（1）函数()f x 求导数，分别求导数大于零小于零的范围，得到单调区间.（2）根据（1）中的单调区间得到最大值.【详解】解：（1）()22f x x x '=-- 当()0f x '>时，1x <-，或2x >；当()0f x '<时，12x -<<．∴()f x 的单调增区间为(),1-∞-，()2,+∞；单调减区间为()1,2-．（2）分析可知()f x 的递增区间是()2,1--，()2,4，递减区间是()1,2-，当1x =-时，()213f -=；当4x =时，()2946f =． 由于()()41f f >-，所以当4x =时，()max 296f x =． 【点睛】 本题考查了函数的单调区间，最大值，意在考查学生的计算能力.21．（1）()f x 在(,0)-∞上单调递减，在(0,)+∞上单调递增；（2）证明见解析.【分析】（1）求出导数，判断导数符号从而确定单调性；（2）设()()23F x f x mx x =--，通过导数判断函数()F x 的单调性，证明()0F x >在1,13x ⎛⎫∈ ⎪⎝⎭上成立即可得证. 【详解】（1）()()22x x f x mx xe x e m '=+=+， 当0m ≥时，令()0f x '>，得0x >；令()0f x '<，得0x <，故()f x 在(,0)-∞上单调递减，在(0,)+∞上单调递增；（2）设233()()(1)1x F x f x mx x x e x =--=--+，则()2()(1)33x x x F x e x e x x e x '=+--=-，设()3x x e x ϕ=-，则()3x x e ϕ'=-， 1,13x ⎛⎫∈ ⎪⎝⎭，()30x e ϕ'∴<-<，()x ϕ∴在1,13⎛⎫ ⎪⎝⎭上单调递减，又1103ϕ⎛⎫=> ⎪⎝⎭，(1)30e ϕ=-<， ()x ϕ∴在1,13⎛⎫ ⎪⎝⎭内存在唯一的零点，设为0x ， 则当013x x <<时，()0x ϕ>，()0F x '>，()F x 单调递增， 当01x x <<时，()0x ϕ<，()0F x '<，()F x 单调递减，又1133126226180327327e F e -⎛⎫=-=> ⎪⎝⎭，(1)0F =， ()0F x ∴>在1,13x ⎛⎫∈ ⎪⎝⎭上成立， ∴当1,13x ⎛⎫∈ ⎪⎝⎭时，23()f x mx x >+. 【点睛】本题考查分类讨论含参函数的单调区间、利用导数证明不等式，属于较难题.22．（1）221169x y +=．（2）[． 【分析】（1）根据曲线的参数方程，消去参数ϕ，即可得到曲线的普通方程；（2）根据曲线的参数方程，求得28cos 3sin x y θθ+=+，再利用三角函数的性质，即可求解.【详解】解：（1）4:(3x cos C y sin θθθ=⎧⎨=⎩为参数)，所以1413x cos y sin θθ⎧=⎪⎪⎨⎪=⎪⎩，平方相加消除θ， 得曲线C 的普通方程为221169x y +=． （2）由曲线4cos :3sin x C y θθ=⎧⎨=⎩得823sin 8cos arctan 3x y θθθ⎛⎫+=+=+ ⎪⎝⎭ ∴当8sin arctan 13θ⎛⎫+= ⎪⎝⎭时，2x y +当8sin arctan 13θ⎛⎫+=- ⎪⎝⎭时，2x y +取得最小值 2x y ∴+的取值范围是[．【点睛】本题主要考查了参数方程与普通方程的互化，以及曲线的参数方程的应用，其中解答中掌握参数方程与普通方程的互化方法，以及合理利用曲线的参数方程是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.。

甘肃省武威市第六中学2021届高三数学上学期第二次阶段性复习过关考试试题理数 学（理）一、选择题(本大题共12小题,每小题5分,共60分) 1.设集合{}2|20M x x x =-->，4|01x N x x -⎧⎫=≤⎨⎬+⎩⎭，则M N =（ ）A. (1,4]-B. [1,4]-C. (1,4]D. (2,4]2.要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象（ ） A ．向左平移6π个单位 B ．向右平移3π个单位 C ．向左平移3π个单位 D ．向右平移6π个单位3. 已知i 为虚数单位，则复数2i1iz =-+在复平面上对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限4.若sin cos 3sin cos αααα+=-，则tan α的值为（ ）A ．2-B ．12-C ．2D ．125.若条件:1p x ≤，且p ⌝是q 的充分不必要条件，则q 能够是（ ）A ．1x >B ．0x >C ．2x ≤D ．10x -<<6.在△ABC 中，∠C=90°，(),1AB k =,()2,3AC =则k 的值是（ ）A ．5B ．5-C ．32 D ．32- 7.已知函数 13)(3--=x x x f ，若关于区间[]23-，上的任意实数21,x x ，都有t x f x f ≤-)()(21，则实数t 的最小值是（ ） A ．20 B ．18 C ． 3 D ．08．ABC ∆中,,A B C 的对边分别是,,a b c 其面积2224a b c S +-=，则角C 的大小是（ ）A ．135B ．90C ．45D ．309．已知函数f (x )＝sin 2x －2sin 2x ＋1，给出下列四个结论：①函数f (x )的最小正周期是2π；②函数f (x )在区间5,88ππ⎡⎤⎢⎥⎣⎦上是减函数；③函数f (x )的图象关于直线8x π=对称；④函数f (x )图象的一个对称中心是,04π⎛⎫⎪⎝⎭．其中正确结论的个数是（ ） A ．1 B ．2 C ．3 D ．4 10.若向量a ，b 的夹角为3π，且2a =，1b =，则a 与2a b +的夹角为 ( ) A ．6π B ．3πC ． 23πD ． 56π11.若1sin()33πα-=，则cos(2)3πα+=（ ）A.79B.23C.23-D.79- 12.设()f x 是定义在R 上的偶函数，且当0x ≥时，()21,0122,1xx x f x x ⎧-+≤<⎪=⎨-≥⎪⎩，若对任意的[],1x m m ∈+，不等式()()1f x f x m -≤+恒成立，则实数m 的最大值是（ ） A ．1-B ．13- C ．12-D ．13二、填空题（本大题共4小题，每小题5分，共20分）13.已知向量()sin ,cos a x x =，()2,1b =且a ∥b ，则tan 2x = .14.设等差数列{}n a 的前n 项和为n S .若136a a +=，416S =，则4a =________． 15.已知函数()()sin (0,0,)2f x A x A πωϕωφ=+>><的部分图象如图所示，则()f x 的解析式为 ．16.已知函数()()()22,03,0x a x f x x ax a x ⎧-≤⎪=⎨-+>⎪⎩有三个不同的零点，则实数a 的取值范畴是________．三、解答题 （共70分，解承诺写出必要的文字说明，证明过程或演算步骤） 17.(本小题12分)已知函数()22sin 23sin cos 3cos f x x x x x =++， x R ∈.（1）求函数()f x 在最小正周期和单调递增区间；第15题图（2）求函数()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.18.(本小题12分)已知等差数列{a n }的前三项为a －1,4,2a ，记前n 项和为S n . （1）设S k ＝2550，求a 和k 的值；（2）设b n ＝S n n，求b 3＋b 7＋b 11＋…＋b 4n －1的值．19.(本小题12分)在ABC ∆中，角,,A B C 所对的边长分别是,,a b c ，且B b a C A c a sin )()sin )(sin (-=+-． （1）求角C 的大小；（2）若7=c ，求ABC ∆面积的最大值．20.(本小题12分) 已知函数2()ln f x a x x =+． （1）当2a =-时，求函数()f x 的单调区间； （2）若函数2()()x g f x x=+在[1,)+∞上是单调递增函数，求实数a 的取值范畴．21.(本小题12分)已知函数ln()()x a f x x-=． （1）若1a = ,确定函数()f x 的零点；（2）若1a =-，证明：函数()f x 是(0,)+∞上的减函数；（3）若曲线()y f x =在点(1,(1))f 处的切线与直线0x y -=平行，求a 的值.22.(本小题10分) 已知曲线C 的极坐标方程是2ρ=,以极点为原点,极轴为x 轴的正半轴建立平面直角坐标系,直线l的参数方程为1221x t y ⎧=-⎪⎪⎨⎪=+⎪⎩ (t 为参数).（1）写出直线l 的一般方程与曲线C 在直角坐标系下的方程； （2）设曲线C 通过伸缩变换'{'2x x y y==得到曲线C ',设曲线C '上任一点为()00,M x y ,求0012y +的取值范畴.数学（理）过关考试（二）答案一、选择题二、填空题 13.34- 14. 7 15.()=2sin 23f x x π⎛⎫- ⎪⎝⎭ 16.4,19⎛⎤⎥⎝⎦三、解答题17.（1）最小正周期T π=， ,,36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ ……………6分（2）最大值4，最小值1. ……………12分 18.解 (1)由已知得a 1＝a －1，a 2＝4，a 3＝2a ，又a 1＋a 3＝2a 2，∴(a －1)＋2a ＝8，即a ＝3. ∴a 1＝2，公差d ＝a 2－a 1＝2. 由S k ＝ka 1＋k (k －1)2d ，得2k ＋k (k －1)2×2＝2 550，即k 2＋k －2 550＝0， 解得k ＝50或k ＝－51(舍去)． ∴a ＝3，k ＝50. ……………6分 (2)由S n ＝na 1＋n (n －1)2d 得S n ＝2n ＋n (n －1)2×2＝n 2＋n .∴b n ＝S n n＝n ＋1，∴{b n }是等差数列， 则b 3＋b 7＋b 11＋…＋b 4n －1＝(3＋1)＋(7＋1)＋(11＋1)＋…＋(4n －1＋1) ＝(4＋4n )n2. ∴b 3＋b 7＋b 11＋…＋b 4n －1＝2n 2＋2n . ……………12分 19. （1）由已知和正弦定理得：()()()a c a c a b b -+=-因此222a c ab b -=-，故222a b c ab +-=，因此cos C ＝2222a b c ab +-＝12因此C=60° ……………6分（2）由（1）得222a b c ab +-=，得2249a b ab +=+，又因为222a b ab +≥令()0f x '>，解得1x >；令()0f x '<，解得01x <<，因此函数()f x 的单调递增区间是()1,+∞，单调递减区间是()0,1……………6分 [1,)+∞上恒成立，即22a x x≥-在[1,)+∞上恒成立． 设22()2x x x ϕ=-， 因为22()2x xx ϕ=-在[1,)+∞上单调递减，因此max 1()()0x ϕϕ==， 因此0a ≥．综上，实数a 的取值范畴为[0,)+∞．……………12分 21解：（1）当1a = 时，则ln(1)()x f x x -=定义域是(1,)+∞，令ln(1)x x -=ln(1)0,2x x -==是所求函数的零点. ……………3分（2）当1a =-时，函数()f x 的定义域是(1,0)(0,)-⋃+∞，因此2ln(1)1'()xx x f x x -++=，令()ln(1)1x g x x x =-++，只需证：0x >时，()0g x ≤． 又2211'()0(1)1(1)x g x x x x =-=-<+++， 故()g x 在(0,)+∞上为减函数，()(0)ln10g x g <=-=，因此'()0f x <，函数()f x 是(0,)+∞上的减函数． ……………7分（3）由题意知，1'()|1x f x ==，且2ln()'()xx a x a f x x---=，因此1'(1)ln(1)11f a a =--=-，即有ln(1)01aa a--=-，令()ln(1)1at a a a=---，1a <，则211'()0(1)1t a a a =+>--， 故()t a 是(,1)-∞上的增函数，又(0)0t =，因此0是()t a 的唯独零点，即方程ln(1)01aa a--=-有唯独实根0，因此0a =． ……………12分22.解:（1）将直线l 的参数方程为1221x t y ⎧=-⎪⎪⎨⎪=⎪⎩ (t 为参数)消参得其一般方程为10y +-=, 将曲线C 的极坐标方程是2ρ=化为直角坐标系下的方程为224x y += ……………5分( 2 ) 曲线C 通过伸缩变换'{'2x xy y ==得到曲线C '的方程为224,4y x +=即221,416x y += 又因为点()00,M x y 曲线C '上,则002cos 4sin x y θθ=⎧⎨=⎩(θ为参数)0012sin 4sin 23y πθθθ⎛⎫+=+=+ ⎪⎝⎭,因此0012y +的取值范畴[]4,4- ……………10分。

2021年甘肃省武威六中高考数学二诊数学试卷（理科）1.选择填空1【考点】交集及其运算．【分析】求解不等式首先求得集合A，然后利用交集的定义求解交集即可．【点评】本题考查了交集的定义，一元二次不等式的解法等，重点考查学生对基础概念的理解和计算能力，属于基础题．2【考点】虚数单位i、复数．【分析】设出复数z，然后利用复数相等的充要条件，求解即可．【点评】本题考查复数的基本运算，复数相等的充要条件的应用，考查计算能力．3【考点】进行简单的合情推理．【分析】由算筹含义直接求解．【点评】本题考查中华传统文化中的数学问题，考查简单的合理推理、推理论证能力等基础知识，考查运用求解能力，考查函数与方程思想，是基础题．4【考点】对数值大小的比较．【分析】利用根式的运算性质、幂函数的单调性可得a，b的大小关系，利用对数函数的单调性即可得出c＜1．【点评】本题考查了根式的运算性质、幂函数的单调性、对数函数的单调性，考查了推理能力与计算能力，属于基础题．5【考点】程序框图．【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，可得答案．【点评】本题主要考查算法的相关知识，难度不大，属于基础题．6【考点】平面向量数量积的性质及其运算．【分析】直接利用向量的数量积公式以及二倍角公式化简求解即可．【点评】本题考查向量的数量积的计算，二倍角公式的应用，是基本知识的考查．7【考点】充分条件、必要条件、充要条件．【分析】已知函数f（x），根据f（x）＝﹣f（x）可知它是奇函数，然后由题意看命题“a+b≥0”与命题f（a）+f（b）≥0”是否能互推，然后根据必要条件、充分条件和充要条件的定义进行判断．【点评】此题主要考查利用函数的导数判断函数的单调性，还考查了必要条件、充分条件和充要条件的定义．8【考点】数列的求和．【分析】设{an}公比为q，运用等比数列的求和公式，解方程可得q，求得数列{log2an}是以log2a1＝2为首项，公差为1的等差数列，由等差数列的求和公式，计算可得所求和．【点评】本题考查等比数列和等差数列的通项公式和求和公式的运用，考查方程思想和运算能力，属于中档题．9【考点】三角形中的几何计算．【分析】由正弦定理，两角和的正弦函数公式化简已知等式可得2sinBcosB＝sinB，结合sinB≠0，可求cosB的值，进而可求B的值，由余弦定理，基本不等式可得：ac≤4，进而利用三角形面积公式即可得解△ABC面积的最大值．【点评】本题考查解三角形的相关知识，考查了正弦定理，余弦定理，基本不等式，三角形面积公式在解三角形中的应用，考查了转化思想，属于中档题．。

2020-2021学年甘肃省武威第六中学高二第一学期第二次学段考试数学（文）试题【含答案】第I 卷（选择题）一、单选题（每小题5分，共60分） 1．抛物线 22x y =- 的焦点坐标是 ( )A ．()1,0-B ．()1,0C ．10,2⎛⎫- ⎪⎝⎭D ．10,2⎛⎫ ⎪⎝⎭2．已知命题:p “2,20x R x x ∀∈-+≥”，则p ⌝是 （ ） A ．x ∀∉R 2,20x x -+>B ．x ∀∉R 200,20x x -+≤C ．0x ∃∈R 200,20x x -+<D ．0x ∀∉R 200,20x x -+≤3．函数()2()2f x x π=的导数是（ ） A ．()4f x x π'= B ．2()4f x x π'=C ．2()8f x xπ='D ．()16f x x π'=4．若3)(0-='x f ，则()()xf x f x x x ∆-∆+→∆000lim=（ ）A ．3-B ．12-C ．9-D ．-65． 设R x ∈，则“21≥x ”是“0122≥-+x x ”的（ ） A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件6． 设2()24ln f x x x x =--，则()f x 的递减区间为（ ）． A ．(1,2)-B ．(0,2)C ．(,1)-∞-，(2,)+∞D ．(2,)+∞7．若双曲线2222:1(0,0)y x C a b a b-=>>3C 的渐近线方程为（ ）A ．12y x =±B ．2y x =C ．2y x =±D ．22y x =±8．独立性检验中，为了调查变量X 与变量Y 的关系，经过计算得到()26.6350.01P κ≥=，表示的意义是（ ） A ．有99%的把握认为变量X 与变量Y 没有关系 B ．有1%的把握认为变量X 与变量Y 有关系 C ．有0.1%的把握认为变量X 与变量Y 没有关系D ．有99%的把握认为变量X 与变量Y 有关系9． 已知12,F F 是椭圆221108x y +=的两个焦点，P 为椭圆上一点，且△12F PF 是直角三角形，则△12F PF 的面积为（ ）.A ．55B ．855C ．55或8 D ．855或8 10．函数()312f x x x =-在区间[]3,3-上的最小值是（）A ．-9B ．-16C ．-12D ．911．已知抛物线E ：28x y =的焦点为F ，过F 的直线l 与E 交于A ，B 两点，与x 轴交于点C .若A 为线段CF 的中点，则AB =（ ）A ．9B ．12C ．18D ．7212． 已知函数()()f x x R ∈满足()11f =，且()f x 的导函数()13f x '<，则()233x f x <+的解集为（ ） A ．{}1x x <- B ．{1x x <-或}1x >C ．{}1x x >D ．{}0x x <第II 卷（非选择题）二、填空题（每小题5分，共20分）13．若方程2211x y m m +=-表示的曲线是椭圆，则m 的取值范围为_________.14． 已知x 与y 之间的一组数据： x2 5 7 10 y1357则y 与x 的线性回归方程为ˆˆˆybx a =+必过点___________. 15．命题“若3a >-，则6a >-”以及它的逆命题，否命题，逆否命题中，真命题的个数为__________________.16． 在平面几何中有如下结论：若正三角形ABC 的内切圆周长为1C ，外接圆周长为2C ，则1212C C =.推广到空间几何可以得到类似结论：若正四面体ABCD 的内切球表面积为1S ，外接球表面积为2S ，则12S S =__________． 三、解答题（共70分）17．已知P （﹣1，1），Q （2，4）是曲线y=x 2上的两点，求与直线PQ 平行且与曲线相切的切线方程．18．设函数2()(1)f x x x =-.（1）讨论()f x 的单调性；（2）当0x ≥时，()2f x ax ≤+恒成立，求a 的取值范围.19． 如表是某位文科生连续5次月考的历史、政治的成绩，结果如下： 月份 9 10 11 12 1 历史（x 分） 79 81 83 85 87 政治（y 分）7779798283（1）求该生5次月考历史成绩的平均分和政治成绩的平均数；（2）一般来说，学生的历史成绩与政治成绩有较强的线性相关关系，根据上表提供的数据，求两个变量,x y 的线性回归方程.参考公式：()()()1122211n niii ii i nniii i x x y y x y nx yb x x xnx====---⋅==--∑∑∑∑a y bx=-，x ，y 表示样本均值.20．已知椭圆216x ＋24y ＝1的弦AB 的中点M 的坐标为(2，1)，求直线AB 的方程及AB 弦长．21． 设函数b ax x x f +-=3)(3．（1）若曲线在点(2,())f x 处与直线8y =相切，求,a b 的值；（2）在（1）的条件下求函数()f x 的单调区间与极值点．22． 已知椭圆2222:1(0)x y C a b a b +=>>过点(2,1)且离心率为22.（1）求椭圆C 的方程；（2）是否存在过点()0,3P 的直线l 与椭圆C 相交于A ，B 两点，且满足2PB PA =．若存在，求出直线l 的方程；若不存在，请说明理由.参考答案一、单选题 题号 123456789101112选项CCCAABDDBBAC二、填空题13．(1,)+∞ 14．(6,4) 15．2 16．19三、解答题17.解：设切点坐标为M （x 0，y 0），则切线斜率为2x 0， 又直线PQ 的斜率为k PQ =4121-+=1， ∵切线与直线PQ 平行， ∴2x 0=1，∴x 0=12， ∴切点为（12，14），切线斜率为1． ∴切线方程为y ﹣14=x ﹣12即4x ﹣4y ﹣1=0．18.解：（1）()2’13f x x =- 令()’0f x =得3333x x =-=， 当3x ∈-∞（时，f ’(x )<0；当33x ∈（，时，f ’(x )>0；当3x ∈+∞（）时，f ’(x )<0.所以f (x )在33x ∈-∞-（，），33+∞）单调递减，在3333-（，）单调递增 （2）由()2f x ax ≤+得32ax x x ≥--,当0x =时，02≥-，显然成立，当0x >,221.a x x≥--令()221g x x x=--,则()22’2g x x x =-+=0得极大值点x=1,g(x)的最大值为g(1)=-2，故，a ≥-2 19.解：（1）根据题意，计算()17981838587835x =⨯++++=， ()17779798283805y =⨯++++=；（2）计算()()5130i i i x x y y =--=∑，()52140i i x x=-=∑，所以回归系数为()()()121300.7540niii nii x x y y b x x ==--===-∑∑， 800.758317.75a y bx =-=-⨯=，故所求的线性回归方程为0.7517.75y x =+. 20.解： 设A (x 1，y 1)，B (x 2，y 2)，x 1≠x 2.∵M (2，1)为线段AB 的中点，∴x 1＋x 2＝4，y 1＋y 2＝2.又A ，B 两点在椭圆上，则22221122416,416x y x y +=+=两式相减，得()()2222121240x x y y -+-=， 于是(x 1＋x 2)(x 1－x 2)＋4(y 1＋y 2)(y 1－y 2)＝0.()12121212414422y y x x x x y y -+∴=-=-=--+⨯即k AB ＝12-故所求直线AB 的方程为x ＋2y －4＝0. 由22240416x y x y +-=⎧⎨+=⎩，得240x x -=， 由根与系数的关系得，12124,0x x x x +=⋅=，所以 2211()4052AB =+--=， 21.解：（Ⅰ）()'233fx x a =-,∵曲线()y f x =在点(2,())f x 处与直线8y =相切，∴()()()'203404,24.86828f a a b a b f ⎧=-=⎧=⎧⎪⎪⇒⇒⎨⎨⎨=-+==⎪⎩⎪⎩⎩ （Ⅱ）∵123)(2'-=x x f , 由20123)(2'±=⇒=-=x x x f ， 当)2,(--∞∈x 时，()'0f x >，函数()f x 单调递增，当)2,2(-∈x 时，()'0fx <，函数()f x 单调递减，当),2(∞+∈x 时，()'0fx >，函数()f x 单调递增，∴此时2-=x 是()f x 的极大值点，2=x 是()f x 的极小值点． 22.解：解：（1）由已知点代入椭圆方程得22211a b+= 由22e =得22c a =可转化为222a b = 由以上两式解得224,2a b ==所以椭圆C 的方程为：22142x y +=.（2）存在这样的直线.当l 的斜率不存在时，显然不满足2PB PA =,所以设所求直线方程:3l y kx =+代入椭圆方程化简得： ()221212140k xkx +++=1221212k x x k +=-+① 1221412x x k =+.② ()2227(12)414120,4k k k ∆=-⨯⨯+>>,设所求直线与椭圆相交两点()()1122,,,A x y B x y 由已知条件2PB PA =可得212x x =,③ 综合上述①②③式子可解得27724k =>符合题意, 所以所求直线方程为：1432y x =±+.。