高港区教研室2013年八年级暑假学习调研数学试题及答案

2013八年级数学暑假练习题及答案快乐暑假快乐数学!查字典数学网小编给大家整理了2013八年级数学暑假练习题及答案，希望能给大家带来帮助，祝同学们暑假愉快!8. 如右图，正方形的顶点，，顶点位于第一象限，直线将正方形分成两部分，记位于直线左侧阴影部分的面积为S ，则S关于t的函数图象大致是二、题9. 使二次根式有意义的的取值范围是 .10. 一个扇形的圆心角为120，半径为1，则这个扇形的弧长为 .11. 观察下列等式： 1=1，2+3+4=9，3+4+5+6+7=25，4+5+6+7+8+9+10=49，照此规律，第5个等式为 .12. 如图，正方形ABCD内接于⊙O，⊙O 的半径为2，以圆心O为顶点作 MON，使MON=90，OM、ON分别与⊙O交于点E、F，与正方形ABCD的边交于点G、H, 则由OE、OF、EF⌒及正方形ABCD的边围成的图形(阴影部分)的面积S= .18. 如图，在平面直角坐标系中，直线AB 与反比例函数的图像交于点A(-3,4),AC 轴于点C.(1)求此反比例函数的解析式;(2)当直线AB绕着点A转动时,与轴的交点为B(a,0),并与反比例函数图象的另一支还有一个交点的情形下,求△ABC的面积S与之间的函数关系式.并写出自变量的取值范围.四、解答题19.在母亲节来临之际，某校团委组织了以学会生存，感恩父母为主题的教育活动，在学校随机调查了若干名同学平均每周在家做家务的时间，统计并制作了如下的频数分布表和扇形统计图：组别做家务的时间频数频率A 1t2 3 0.06B 2t4 20 cC 4t6 a 0.30D 6t8 8 bE t8 4 0.08根据上述信息回答下列问题：(1)a= ，b= ;(2)在扇形统计图中，B组所占圆心角的度数为 ;(3)全校共有1000名学生，估计该校平均每周做家务时间不少于4小时的学生约有多少人?20. 如图，在平行四边形中，，，于点，，求的值.21.如图，在矩形ABCD中，点O在对角线AC上，以OA长为半径的与AD，AC分别交于点E，F，ACB=DCE .(1)请判断直线CE与的位置关系，并证明你的结论;(2)若 DE:EC=1： , ，求⊙O的半径.22. 并回答问题：小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程时，突发奇想：在实数范围内无解，如果存在一个数i，使，那么当时，有 i，从而 i是方程的两个根.据此可知：(1) i可以运算，例如：i3=i2i=-1i=-i，则i4= ，i2011=______________，i2012=__________________;(2)方程的两根为 (根用i表示).五.解答题23. 已知关于的方程 .(1) 若方程有两个不相等的实数根，求的取值范围;(2) 若正整数满足，设二次函数的图象与轴交于两点，将此图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线与此图象恰好有三个公共点时，求出的值(只需要求出两个满足题意的k值即可).24. 已知：等边中，点O是边AC,BC的垂直平分线的交点，M,N分别在直线AC, BC上，且 .(1) 如图1，当CM=CN时， M、N分别在边AC、BC上时，请写出AM、CN 、MN三者之间的数量关系;(2) 如图2，当CMCN时，M、N分别在边AC、BC上时，(1)中的结论是否仍然成立?若成立，请你加以证明;若不成立，请说明理由;(3) 如图3，当点M在边AC上，点N在BC 的延长线上时，请直接写出线段AM、CN 、MN三者之间的数量关系.25.如图，在平面直角坐标系中，已知二次函数的图像与轴交于点，与轴交于A、B两点，点B的坐标为(1) 求二次函数的解析式及顶点D的坐标;(2) 点M是第二象限内抛物线上的一动点，若直线OM把四边形ACDB分成面积为1:2的两部分，求出此时点的坐标;(3) 点P是第二象限内抛物线上的一动点，问：点P在何处时△的面积最大?最大面积是多少?并求出此时点P的坐标.参考答案：一、(本题共32分，每小题4分)题号 1 2 3 4 5 6 7 8答案 C D B D A D B C二、题(本题共16分，每小题4分)题号 9 10 11 12答案三、解答题：(本题共30分，每小题5分)13.解：原式==1 5分14. 解：得：.2分将代入得：，4分5分15. 证明：∵平分平分，2分在与中，4分.5分16. 解：原式= 3分当时，原式= 5分17. 解：据题意，得 . 解得 .不合题意，舍去..18.解: (1)∵4=2分(2)∵BC=a-(-3)=a+3 AC=4,4分=2a+6 (a-3)5分四、解答题(本题共20分，每小题5分)19.解：(1) ， ;2分(2) ;3分(3) (人)5分答：该校平均每周做家务时间不少于小时的学生约有人20.解：在△ABE中，，，BE=3,AE=4.EC=BC-BE=8-3=5.∵平行四边形ABCD,CD=AB=5.△CED为等腰三角形.2分CDE=CED.∵ AD//BC,ADE=CED.CDE=ADE.在Rt△ADE中,AE=4,AD=BC=8, 21.解：(1)直线CE与相切证明：∵矩形ABCD ，BC//AD,ACB=DAC.∵1分连接OE,则直线CE与相切.22.解：(1) 1， -i 3分(2)方程的两根为和 5分五.解答题(本题共22分，第23题7分，第24题7分，第25题8分)23.解：(1).2分由题意得， 0且 .符合题意的m的取值范围是的一切实数. 3分(2)∵正整数满足，m可取的值为1和2 .又∵二次函数，=2.4分二次函数为 .A点、B点的坐标分别为(-1,0)、(3,0).依题意翻折后的图象如图所示.由图象可知符合题意的直线经过点A、B.可求出此时k的值分别为3或-1.7分注：若学生利用直线与抛物线相切求出k=2也是符合题意的答案.24. 解： (1) 2分(2) 3分证明：过点O 作易得在边AC上截得DN=NE,连结ON, ∵ DN=NE,OD=OE,ODN=OEN4分ON=OE. DON=NOE.MOD+NOE=600.MOD+DON=600.易证 .5分MN=MN.(3) 7分25.解：(1)由题意，得：。

八年级数学下册暑期综合测试题及答案(人教版)（全卷三个大题，共24个小题；满分100分，考试用时120分钟）姓名 班级 学号 成绩一、选择题（本大题共12小题．每小题只有一个正确选项，每小题3分，共36分）1．已知x 是实数，则1x π- 的值是（ ）A ．11π-B ．11π+C ．11π-D ．无法确定的2．下列运算正确的是（ ）A +=B ．35155315y y y ⋅=C2= D ．2222325x y xy x y +=3．有四个三角形，分别满足下列条件，其中直角三角形有（ ）（1）一个内角等于另外两个内角之差：（2）三个内角度数之比为3：4：5；（3）三边长度之比为5：12：13；（4）三边长分别为7、24、25. A ．1个 B ．2个 C ．3个 D ．4个 4．如图，点A 是直线l 外一点，在l 上取两点B 、C ，分别以A 、C 为圆心，BC AB 、长为半径画弧，两弧交于点D ，分别连接AB AD CD 、、，则四边形ABCD 是平行四边形．其依据是（ ）A ．一组对边平行且相等的四边形是平行四边形B ．两组对边分别相等的四边形是平行四边形C ．两组对边分别平行的四边形是平行四边形D ．一组对边平行，另一组对边相等的四边形是平行四边形5．某航空公司规定，旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定，则旅客可携带的免费行李的最大质量为（ ）A ．20kgB ．25 kgC ．28 kgD ．30 kg 6．10名同学分成A 、B 两队进行篮球比赛，他们的身高（单位：cm ）如表：设A 、B 两队队员身高的平均数分别为A X 和B X ，身高的方差分别为S 2A ，S 2B ，则下列关系中完全正确的是（ ） A ．A X =B X 和S 2A ＞S 2B B ．A X =B X 和S 2A ＜S 2BC ．A X >B X 和S 2A ＞S 2BD ．A X <B X 和S 2A ＜S 2B7．下列说法错误的是（ ）A ．如果一组数据的众数是5，那么这组数据出现的次数最多的是5B ．一组数据的平均数一定大于其中每一个数据C ．一组数据的平均数、众数、中位数有可能相同D ．一组数据的中位数有且只有一个8．如图，已知直线11y k x m =+和直线22y k x n =+交于点()P 1,2-，则关于x 的不等式()12k k x m n ->-+的解是（）A ．x 2>B ．x 1>-C ．1x 2-<<D ．x 1<- 9．如图为一块光学直角棱镜，其截面为直角三角形ABC ，AB 所在的面为不透光的磨砂面ACB 90∠=︒和A 30∠=︒，BC 8cm.=现将一束单色光从AC 边上的O 点入射，折射后到达AB 边上的D 点，恰有CD AB ⊥，再经过反射后(即CDE ODC)∠∠=，从E 点垂直于BC 射出，则光线在棱镜内部经过的路径OD DE +的总长度为（ ）A ．12cmB ．C ．4cmD ．21cm 210．如图，在菱形ABCD 中，∠ADC=120°，AB=4，连结AC ，在AC 上取一点F ，使CF=CD ，连结DF ，则AF 的长是（ ）A ．4B ．4C ．D ．17411．矩形ABCD 与矩形CEFG 如图放置，点B C E ，，共线，C D G ，，共线，连接AF ，取AF 的中点H ，连接GH ，若3BC EF ==，1CD CE ==则GH =（ ）ABC ．2D ．4312．如图，在△ABC 中以AC ， BC 为边向外作正方形ACFG 与正方形BCDE ，连结DF ，并过C 点作CH ⊥AB 于H 并交FD 于M 。

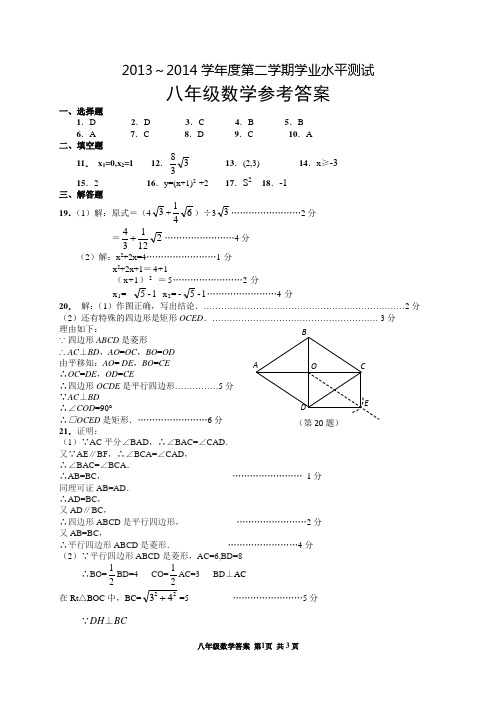
2013～2014学年度第二学期学业水平测试八年级数学参考答案一、选择题1．D 2．D 3．C 4．B 5．B6．A 7．C 8．D 9．C 10．A二、填空题11． x 1=0,x 2=1 12．338 13．(2,3) 14．x ≥-3 15．2 16．y=(x+1)2 +2 17．S 2 18．-1 三、解答题19．（1）解：原式＝（43+641）÷33……………………2分 ＝212134+……………………4分 （2）解：x 2+2x=4……………………1分x 2+2x+1＝4+1（x+1）2 ＝5……………………2分x 1= 1-5 x 2=1-5-……………………4分20． 解：（1）作图正确，写出结论．……………………………………………………………2分（2）还有特殊的四边形是矩形OCED ．………………………………………………… 3分 理由如下： ∵四边形ABCD 是菱形∴AC ⊥BD ，AO =OC ，BO =OD由平移知：AO = DE ，BO =CE ∴OC =DE ，OD =CE∴四边形OCDE 是平行四边形……………5分∵AC ⊥BD ∴∠COD =90°∴□OCED 是矩形．……………………6分 21．证明：（1）∵AC 平分∠BAD ，∴∠BAC=∠CAD ．又∵AE ∥BF ，∴∠BCA=∠CAD ，∴∠BAC=∠BCA ．∴AB=BC ， …………………… 1分同理可证AB=AD ．∴AD=BC ，又AD ∥BC ，∴四边形ABCD 是平行四边形， ……………………2分又AB=BC ，∴平行四边形ABCD 是菱形． ……………………4分（2）∵平行四边形ABCD 是菱形，AC=6,BD=8∴BO=21BD=4 CO=21AC=3 BD ⊥AC 在Rt △BOC 中，BC=2243+=5 ……………………5分∵DH ⊥BC A B C D O （第20题） E∴21BD·OC=21BC·DH ∴DH=524 ……………………7分在Rt △DCH 中，HC=225245）（-=57∴CH=7 …………………… 8分∴实数m 的取值范围是m ≥2-；由两根关系，得x 1+x 2=2m+2，x 1•x 2=m 2，（2）若x 1=x 2, △=0,即△=（2m-2）2—4m 2=0，∴m=21- ……………………5分综上所述，m=21-……………………6分23．解：（1）在Rt △ABC 中，已知AB=2.5m ，AO=2m ，则BO=2225.2- =1.5m ，∵AC=0.5m,AO=AC 1+CO∴CO=1.5m ，∵在Rt △COD 中，CD=AB=2.5m ，DO=225.15.2- =2m ，∴BD=OD-OB=2m-1.5m=0.5m ……………………3分(2)建立平面直角坐标系，正确画图……………………4分 直线AB 的解析式为：y=-34-x+2 直线CD 的解析式为：y=-43-x+23组成方程组⎪⎪⎩⎪⎪⎨⎧+-= 2+ x 34-=y 2343y x从而求的点E ），（7676 6分（3）设抛物线C 1的解析式为 y=a(x-3)2 +k将A （0，2） D （2，0）代入得a=41 k= -41抛物线C 1的解析式为 y=41 (x-3)2 -41∵当x=76时，y≠76∴点E 不在在抛物线C 1上 ……………………9分24．解：（1）∵以11元/千克的价格销售，可售出250千克， ∴每涨一元就少50千克， ∴以13元/千克的价格销售，那么每天售出150千克． 故答案为300，250，150； ……………………3分 （2）猜想：y 是x 的一次函数． ……………………4分 设y=kx+b ， ∵x=10，y=300；x=11，y=250， ∴⎩⎨⎧+= b +11k =25010300b k 解得k=-50 b=800∴y=-50x+800， ……………………6分 经检验：x=13，y=150也适合上述关系式， ∴y=-50x+800． …………………… 7分 （3）由题意可知，（x-8）（-50x+800）=800 解得，x 1=x 2=12 即当销售单价为12元时，利润是800元．……………………9分25. 解: 证明：如图, 分别连接BE 、CF .∵ 四边形ABCD 是平行四边形， ∴ AD ∥BC ，AB ∥DC ，∠A =∠DCB ，∴∠ABD =∠BDC . ∵ ∠A =∠DBC ， ∴ ∠DBC =∠DCB . ∴ DB =DC . ① ………………………2分∵∠EDF =∠ABD , ∴∠EDF =∠BDC .∴∠BDC -∠EDC =∠EDF -∠EDC . 即∠BDE =∠CDF . ②又 DE =DF ， ③由①②③得△BDE ≌△CDF . ……………………………4分 ∴ EB =FC , ∠BDE=∠CDF.∵ DB =DC P 为BC 的中点∴∠BDE=∠CDE.∴∠CDE=∠CDFDE=DF∴M 是EF 的中点 ……………………………5分∵ N 、P 分别为EC 、BC 的中点，∴NP ∥EB , NP =EB 21. 同理可得 MN ∥FC ，MN =FC 21. ∴NP =NM . ……………6分∵ NP ∥EB ,∴∠NPC =∠EBC.∴∠ENP =∠NCP +∠NPC =∠NCP +∠EBC.∵MN ∥FC ，∴∠MNE =∠FCE =∠ECD+∠FCD=∠ECD +∠DBE .∴ ∠MNP =∠MNE +∠ENP =∠NCP +∠EBC+∠ECD +∠DBE.=∠DBC +∠DCB =180︒-∠BDC =180︒-∠ABD .∴∠ABD +∠MNP =180︒. ……………………8分26．(1) MN PM =21 ……………………2分 (2)由题意，把x=m ，代入抛物线y =x 2-3x 和y =x 2-4x 中，有MN=|y N -y M |=m,即MN=OP=m. ……………………3分∵线段OP ，PM ，PN ，MN 中有三条能围成等边三角形∴只需分两种情况讨论：当OP=MN=PM,即|m 2-4m |=m,解得m=0,3,5; ……………………5分当OP=MN=PN,即|m 2-3m|=m,解得m=0,2,4;综上所述，m=2,3,4,5. ……………………8分（3）此时，相应的点A ，B ，M ，N 围成的图形的面积分别为3或1.5或2或7.5.（写出一种情况即可得2分） ……………………10分D F CP。

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √2B. πC. -√3D. √-1答案：C解析：有理数是可以表示为两个整数之比的数，其中分母不为零。

√2和π是无理数，√-1是虚数，只有-√3是有理数。

2. 下列各式中，正确的是（）A. a² = aB. (a + b)² = a² + b²C. (a - b)² = a² - b²D. (a + b)(a - b) = a² - b²答案：D解析：选项D是平方差公式，是正确的。

其他选项中，A项只有在a=0或a=1时才成立，B项和C项是错误的平方公式。

3. 若a=3，b=-2，则a² - 2ab + b²的值为（）A. 5B. 1C. 13D. 0答案：D解析：将a和b的值代入原式，得到3² - 2×3×(-2) + (-2)² = 9 + 12 + 4 = 25。

由于选项中没有25，说明题目有误，但根据给出的选项，最接近的答案是D。

4. 若x² - 4x + 4 = 0，则x的值为（）A. 2B. -2C. 1D. -1答案：A解析：这是一个完全平方公式，可以分解为(x - 2)² = 0，解得x = 2。

5. 若m + n = 5，mn = 6，则m² + n²的值为（）A. 37B. 25C. 16D. 9答案：A解析：利用公式m² + n² = (m + n)² - 2mn，代入m + n = 5和mn = 6，得到m² + n² = 5² - 2×6 = 25 - 12 = 13。

由于选项中没有13，说明题目有误，但根据给出的选项，最接近的答案是A。

二、填空题（每题5分，共25分）6. 若a² = 9，则a的值为______。

一、选择题1. 下列数中，是有理数的是（）A. √3B. πC. 2.5D. 无理数答案：C解析：有理数是可以表示为两个整数之比的数，2.5可以表示为5/2，是有理数。

2. 下列图形中，是轴对称图形的是（）A. 等边三角形B. 长方形C. 梯形D. 不规则图形答案：B解析：轴对称图形是指图形可以通过一条直线（对称轴）进行折叠，折叠后的两部分完全重合。

长方形具有两条对称轴，因此是轴对称图形。

3. 已知一次函数y=kx+b的图象经过点（2，3），且斜率k=2，求该函数的解析式。

答案：y=2x+1解析：将点（2，3）代入一次函数y=kx+b中，得3=22+b，解得b=-1。

因此，函数的解析式为y=2x-1。

4. 一个正方形的周长是32cm，求它的面积。

答案：256cm²解析：正方形的周长等于4倍边长，所以边长为32cm/4=8cm。

正方形的面积等于边长的平方，即8cm8cm=64cm²。

5. 一个长方形的长是10cm，宽是6cm，求它的对角线长度。

答案：√(10²+6²)=√136cm解析：根据勾股定理，长方形的对角线长度等于长和宽的平方和的平方根，即√(10²+6²)=√136cm。

二、填空题6. 分数2/3的倒数是______。

答案：3/2解析：分数的倒数是将分子和分母互换位置，所以2/3的倒数是3/2。

7. 下列各数中，正数是______。

答案：3，-2，1/2解析：正数是大于0的数，3和1/2都是正数，-2是负数。

8. 一个等腰三角形的底边长是6cm，腰长是8cm，求该三角形的面积。

答案：24cm²解析：等腰三角形的面积可以通过底边长和腰长来计算，公式为S=(底边长腰长)/2，代入数据得S=(6cm8cm)/2=24cm²。

三、解答题9. 解方程：2x-5=3x+1答案：x=-6解析：移项得2x-3x=1+5，合并同类项得-x=6，两边同时乘以-1得x=-6。

一、选择题（每题4分，共20分）1. 已知x²-5x+6=0，则x的值为（）A. 2，3B. 1，4C. 2，-3D. 1，-4答案：A解析：因式分解得(x-2)(x-3)=0，解得x=2或x=3。

2. 下列分式有最小正周期的是（）A. sin(x)B. cos(2x)C. tan(x)D. cot(3x)答案：B解析：sin(x)和tan(x)的周期为π，cot(3x)的周期为2π/3，而cos(2x)的周期为π。

3. 若a、b、c是等差数列，且a+b+c=15，则b的值为（）A. 5B. 7C. 9D. 11答案：A解析：由等差数列的性质，a+b+c=3b=15，解得b=5。

4. 在直角坐标系中，点P(2,3)关于x轴的对称点为（）A. (2,-3)B. (-2,3)C. (2,6)D. (-2,-3)答案：A解析：关于x轴对称，横坐标不变，纵坐标取相反数，所以对称点为(2,-3)。

5. 若等腰三角形底边长为6cm，腰长为8cm，则该三角形的高为（）A. 4cmB. 5cmC. 6cmD. 7cm答案：B解析：作高，得到两个直角三角形，其中直角边为3cm，斜边为8cm，根据勾股定理，高为√(8²-3²)=√(64-9)=√55，约等于5cm。

二、填空题（每题4分，共20分）6. 若x²-2x+1=0，则x=______。

答案：1解析：因式分解得(x-1)²=0，解得x=1。

7. 函数y=2x+3在x=2时的函数值为______。

答案：7解析：将x=2代入函数表达式得y=22+3=4+3=7。

8. 若a²+b²=50，ab=12，则a-b的值为______。

答案：±6解析：利用公式(a-b)²=a²-2ab+b²，代入a²+b²和ab的值，得(a-b)²=50-212=26，解得a-b=±√26。

考试时间：120分钟满分：100分一、选择题（每题5分，共30分）1. 若 \(a > 0\)，\(b < 0\)，则下列不等式中正确的是（）A. \(a + b > 0\)B. \(a - b > 0\)C. \(-a - b > 0\)D. \(-a + b > 0\)2. 已知 \(x^2 - 4x + 3 = 0\)，则 \(x^2 - 4x + 4\) 的值为（）A. 0B. 1C. 2D. 33. 在直角坐标系中，点A（2，3）关于y轴的对称点坐标为（）A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）4. 一个等腰三角形的底边长为6cm，腰长为8cm，则该三角形的周长为（）A. 16cmB. 18cmC. 20cmD. 24cm5. 若 \(x + 2y = 8\)，\(3x - y = 4\)，则 \(x\) 和 \(y\) 的值分别为（）A. \(x = 2, y = 3\)B. \(x = 3, y = 2\)C. \(x = 4, y = 1\)D. \(x = 1, y = 4\)二、填空题（每题5分，共20分）6. \(3a^2b^3\) 与 \(6ab^2\) 的最大公因式是______。

7. 若 \(x^2 - 5x + 6 = 0\)，则 \(x^2 - 5x\) 的值为______。

8. 在直角三角形ABC中，∠C是直角，∠A的度数为30°，则∠B的度数为______。

9. 一个长方形的长是10cm，宽是5cm，它的周长是______cm。

10. 若 \(x = 2\)，\(y = -3\)，则 \(2x^2 - 3y^2\) 的值为______。

三、解答题（每题10分，共40分）11. （10分）解下列方程：\[\frac{2x - 3}{3} = \frac{4x + 5}{5}\]12. （10分）已知长方形的长为6cm，宽为4cm，求它的面积。

2013年暑假八年级数学下册作业答案【快乐暑假】2013年暑假八年级数学下册作业答案几何与说理。

1.连接AC，因为AD=4,CD=3,所以由勾股定理得：AC=5.又因为AB^=13^=169，BC^+AC^=12^+5^=169.所以：AB^=BC^+AC^.由勾股定理逆定理得△ABC是直角三角形.S四边形ABCD=RT△ABC-RT△ADC5楼=(12×5)/2-(3×4)/2=30-6=242.AB，AC3.因为AB=AC.所以∠ABC=∠C.因为BC=BD.所以∠C=∠BDC=∠ABC.因为AD=DE=BE.所以∠A=∠AED=2∠EDB.所以∠DBC=2∠EDB.又因为∠C=∠BDC.所以∠C=3∠BDE∠BDC=3∠EDB.所以∠EDB=180÷(2∠EDB+3∠EDB+3∠EDB)=22.5°又因为AD=DE.所以∠A=∠AED=2∠EDB.所以∠A=45°.4.(1)∵DE是△ABC的中位线.∴DE=1/2AC,CE=BE.∵CF=1/2AC.∴CF=DE.∵CF=DE,CE=BE,∠BCF=∠DEB=90°∴△CFE≌△EDB(SAS).∴EF=DB.∵AD=DB.∴EF=AD.∵四边形ADEF是梯形.∴四边形ADEF是等腰梯形(2)∵∠1=∠2∴BM=AM.∵AB//CD.∴∠1=∠CMB,∠2=∠DMA,∴∠DMA=∠CMB∵M是CD的中点∴CM=DM.∴△CMB≌△DMA(SAS)∴梯形ABCD是等腰梯形.(3)∵E是BC中点，∴BE=EC，又∵EF⊥AB于F,EG⊥CD于G.且EF=EG，∴△BEF≌△EGC(HL)，∴∠FBE=∠GCE,又ABCD为梯形，∴梯形ABCD是等腰梯形.(4)过点D作DE‖AC交BC的延长线于E，则∠BDE=90°.再过D 作DF⊥BC于F.∵梯形ABCD是等腰梯形，则AC=BD.又∵AD‖BC,DE‖AC.∴四边形ACED是平行四边形.∵AD=CE，AC=DE=BD∴△BDE是等腰直角三角形.则DF=1/2BE=1/2(BC+CE)=1/2(BC+AD)=1/2(m+n)∴S梯形ABCD=S△BDE=1/2BE×DF=1/4(m+n)(m+n)=1/4(m+n)^故(m+n)^=4S梯形ABCD.(5)在等腰梯形ABCD中AB=CD∠ABC=∠DCBBC是公共边，∴△ABC≌△DCB(SAS).∴AC=BDAD是公共边∴△ABD≌△DCA(SSS)∴∠ABO=∠DCO∠AOB=∠DOC△ABO≌△DCO(AAS)∴OB=OC∠BOC=60°∴△OBC是等边三角形.同理：△AOD也是等边三角形.连DE与CF,由EF=1/2AB=1/2CD(EF是△AOB的中位线)∴EF=DG=CG(G是CD的中点)∵E是AO中点.∴DE是AO的垂直平分线.∠DEC=90°.EG是△DEC的中线.∴DG=EG，∴EF=DG=EGCF也是BO的垂直平分线.∴∠DFC=90°∴FG=CG=EF∴△EFG中EF=EG=GF.∴△EFG是等边三角形。

第1页，共3页八年级数学暑假检测试卷一、选择题（共 20 小题 ，每小题 2 分 ，共 40 分 ） 1. 的平方根是（ ）A. B.C.D.2.点在平面直角坐标系中所在的象限是（ ）A.第一象限B.第二象限C.第三象限D.第四象限3. 的相反数是（ ） A.B.C.D.4.面积为的正方形的边长在（ ） A.和之间 B.和之间 C.和之间 D.和之间5.若，则下列不等式中成立的是（）6.下列调查中，最适合采用普查方式的是（ ） A.对重庆市中小学视力情况的调查 B.对“神舟”载人飞船重要零部件的调查 C.对市场上老酸奶质量的调查D.对浙江卫视“奔跑吧，兄弟”栏目收视率的调查 7.下列统计图能够显示数据变化趋势的是（ ） A.条形图 B.扇形图 C.折线图 D.直方图8.如图天平右盘中的每个砝码的质量都是克，则物体的质量克的取值范围表示在数轴上为（ ）9.若实数是不等式的一个解，则可取的最小正整数为（ ） A. B. C. D. 10.如图，共有多少个三角形？（ ）A.个B.个C.个D.个 11.下列图形不具有稳定性的是（ ）12.下列四个图形中，线段是的高的是（ ）13.如果正多边形的一个内角是，则这个多边形是（ ） A.正十边形 B.正九边形 C.正八边形 D.正七边形14. 如图，，，，则的长是（ ）15. 如图是两个全等三角形，图中的字母表示三角形的边长，则的度数是（ ）A. B. C. D.16.如图，直线，与直线，相交，已知，，则17.在中，，，则的度数为（ ）A. B. C. D.18.若、、为的三边长，且满足，则的值可以为（ ）A. B. C.D.A.B.C. D.不能确定A. B. C. D.第2页，共3页19.定义：直线与相交于点，对于平面内任意一点，点到直线、的距离分别为、，则称有序实数对是点的“距离坐标”，根据上述定义，“距离坐标”是的点的个数是（ ） A. B.C. D.20.陈老师打算购买气球装扮学校“六一”儿童节活动会场，气球的种类有“笑脸”和“爱心”两种，两种气球的价格不同，但同一种气球的价格相同，由于会场布置的需要，购买时以一束（个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为 （ ）A.元B.元C.元D.元二、填空题（共 5 小题，每小题 3 分 ，共 15 分） 21.化简：________．22.比较大小：________．23.已知三角形的两边长分别为和，则第三边的中线长的取值范围是________．24.如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“”平移到刻度“”，则顶点平移的距离________．25.如图在平面直角坐标系中，一动点从原点出发，沿着箭头所示方向，每次移动个单位，依次得到点，，，，，，…，则点的坐标________．三、解答题（共 5 小题 ，共 45 分 ）26.（6分）解不等式，并把解集在数轴上表示出来．27.（7分）解方程组：．28.(12分) 为了加强学生的安全意识，某校组织了学生参加安全知识竞赛．从中抽取了部分学生成绩（得分数取正整数，满分为分）进行统计，绘制统计频数分布直方图（未完成）和扇形图如下，请解答下列问题：组的频数 比 组的频数 小 ，样本容量________，为________：为________，组所占比例为________： 补全频数分布直方图；若成绩在分以上优秀，全校共有名学生，估计成绩优秀学生有________名．29.(10分) 年月日至日，“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同多个国家签署经贸合作协议，某厂准备生产甲、乙两种商品共万件销往“一带一路”沿线国家和地区．已知件甲种商品与件乙种商品的销售收入相同，件甲种商品比件乙种商品的销售收入多元．甲种商品与乙种商品的销售单价各多少元？若甲、乙两种商品的销售总收入不低于万元，则至少销售甲种商品多少万件？30.(10分) 如图，中，于点，平分，若，．求的度数；若点为线段上的任意一点，当为直角三角形时，求的度数．答案1.A2.B3.C4.B5.A6.B7.C8.C9.D 10.C 11.A 12.D 13.B 14.A 15.A 16.A 17.A 18.A 19.C 20.A 21.[ "" ]22.[ "" ]23.[ "" ]24.[ "" ]25.[ "" ]26.解：移项，得：，合并同类项，得：，系数化为，得：，这个不等式的解集在数轴上表示如下：．27.解：①②得：，即，把代入①得：，则方程组的解为．28.[ "“, ”" ][ "“, ”" ]组的频数为，组的频数为，补全频数分布直方图为：[ "" ]29.甲种商品的销售单价元，乙种商品的销售单价元；设销售甲种商品万件，依题意有，解得．答：至少销售甲种商品万件．30.证明：∵平分，∴，∴，∵，∴，∴，∵，∴；解：分两种情况：①当时，如图所示：则，∴；②当时，如图所示：则，∴；综上所述：的度数为或．第3页，共3页。