曲面积分与高斯公式

利用高斯公式，
v v v v u dS [ ( u ) ( u ) ( u )]dxdydz , x x y y z z n u v u v u v uvdxdydz ( )dxdydz x x y y z z
Dxy
sin( xy )dxdy
======0
奇偶对称
I
0


0
184 I1 I 2 35
机动 目录 上页 下页 返回 结束
例3：计算曲面积分
其中, r
2 2 2 2 : x y z R 取外侧 . x y z ,
2 2 2
解: 不能直接用高斯公式
第六节 高斯公式与散度
一、高斯公式
第十章
二、曲面积分与 曲面无关的条件
三、通量与散度
机动
目录
上页
下页
返回
结束
一、高 斯 公 式
说明：
若 可表成：
( x , y ) | z1 ( x , y ) z z2 ( x , y ), ( x , y ) Dxy
则称 是 xy 型空间区域；
r
在椭球面内作辅助小球面
x2 y2 z2
z

1 : x 2 y 2 z 2 2
1
y
x
0

高斯公式
1

3
3 d x d y d z
1
机动 目录 上页 下页 返回 结束
例3**：计算曲面积分
其中 r
x2 y2 z2 ,
: 任意不经过原点的封闭 曲面， 取外侧 .
机动
目录

高斯公式 仍成立. 好抵消，因而
例1 利用高斯公式计算曲面积分：

( x y )dxdy ( y z ) xdydz
其中 为柱面x 2 y 2 1及平面z 0, z 3所围成的空间 闭区域Ω的整个边界曲面的外侧 .
解:因由已知： P ( y-z ) x , Q 0,
2 2 2
xy
而 (简写)
1 1
π , cos 0, cos 0, cos 1 2
( x cos y cos z cos )ds
2 2 2
1
z ds h dxdy πh
或
P Q R x y z dv ( P cos Q cos R cos )dS

此时， 是Ω的整个边界曲面的外侧， 、 、 cos cos cos 是 上点( x，y，z )处的法向量的方向余弦，以上 二式称为 高斯公式 .
D xy
对于(1)与(2)式，同样可得:
如果穿过Ω内部，且平行于x轴的直线与Ω的边界曲 面 的 交点恰好为两个，
P 有： x dv P( x, y, z )dydz 成立. Ω
如果穿过Ω内部，且平行于y轴的直线与Ω的边界 曲面的 交点恰好为两个，
Q 有： dv Q( x, y, z )dzdx 成立. y
z z 2 ( x, y )
z1 ( x, y ) z 2 ( x, y )
(4) 1取下侧， 2 取上侧， 3是以Dxy的边界 曲线为准 线， 母线平行于z轴的柱面上的一 部分，取外侧.
则(3)式左边：
z2 ( x , y ) R R z dv z dz dxdy Ω Dxy z1 ( x , y ) Rx, y, z 2 ( x, y ) Rx, y, z1 ( x, y )dxdy

a
- x2
= ò dq ò (
0 0
- r 2 cos 2 q a -r
2 a 2
+ 2a 2 - 2a a 2 - r 2 - r 2 )rdr
= -4 ò 2 cos 2 q dq ò
0
p
0
1 + p a3 6 a -r
2 2
r 3 dr
p p 1 1 = -4a 3 ò 2 cos 2 q dq ò 2 sin 3 tdt + p a 3 = - p a3 0 0 6 2
r ur uuuuu I = òò Pdydz + Qdxdz + Rdxdy = òò {P, Q, R} ×{dydz, dxdz, dxdy} = òò F × n 0 dS
S
S
U
注意：曲面前侧取“正” ，后侧取“负” ；右侧取“正” ，左侧取“负” ；上侧取“正” ，下侧 取“负” ． 三、向量点积法（转换投影法）
2 2 2
曲面 S 在 xoy 平面的投影域为 Dxy = {( y, z ) | x + y £ 1} ，
2 2
而
òò xdydz = òò
S
S前(向后)
xdydz + òò xdydz
S后
D yz
is
Dyz
= - òò a 2 - y 2 - z 2 dydz - òò a 2 - y 2 - z 2 dydz
曲面 S：z = - a - x - y ,
2 2 2
U
r n = {- f x¢ , - f y¢ ,1} = {
nR
=
1 1 ( z + a ) 2 dxdy = òò (a - a 2 - x 2 - y 2 ) 2 dxdy òò a S a Dxy

(非闭曲面时注意添加辅助面的技巧) (2) 推出闭曲面积分为零的充要条件:
应用: (1) 计算曲面积分
∫∫Σ Pd y d z + Qd z d x + Rd xd y = 0
∂P ∂Q ∂R + + =0 ∂x ∂ y ∂z
作业
273页 16（2）（6） 274页 (B) 6
沿任意闭曲面的曲面积分为零的条件
z = − 1 − x 2 − y 2 的上侧 计算 的上侧, 例5. 设∑为下半球面
解 :设
∑
∑1 : z = 0, x 2 + y 2 ≤ 1
z
,取上侧
I = ∫∫ x sin 2 (1 − z )dydz + y cos 2 (1 − z )dzdx
y
− z dxdy
∑1
′ P′ + Q′ + Rz = 0 x y
y
− z dxdy
=0
∑1
′ P′ + Q′ + Rz = 0 x y
x
= ∫∫ x sin 2 (1 − z )dydz + y cos 2 (1 − z )dzdx − z dxdy
y
∑
∴ I = I1 + ∫∫ ( − 6 z )dxdy
1 x
内容小结
1. 高斯公式及其应用 公式:
∫∫Σ Pd y d z + Qd z d x + Rd xd y ∂P ∂Q ∂R )d xd y d z = ∫∫∫ ( + + Ω ∂x ∂ y ∂z
= ∫∫ Pd y d z + Qd z d x + Rdx d y
Σ
(Gauss 公式 公式)

曲 利用Gauss 公式, 得 线 积 原式 = ( y z ) d x d y d z (用柱坐标) 分 与 曲 ( z )dxdy d z ( z ) d d d z 面 积 9 2 1 3 分 d d ( z ) dz 0 0 0 2
1 2 3 , 1 : z z1 ( x , y ) ,
第 十则 章 曲 线 积 分 与 曲 面 积 分
2 : z z2 ( x , y ),
z
z
z d x d y d z d x d y z ( x , y )

1
R
z2 ( x , y ) R

流速场，穿过有向曲面 的流量


v n dS
电位移为 D
电场，穿过有向曲面 的电通量

磁感应强度为 B 磁场，穿过有向曲面 B dS B n dS


D dS

D n dS
2 ( x y z )dxdydz h dS
2

2
, 0, z h

Dxy
z
1
h

2
2
d
0
0
h
d zdz h 4

h
h 2
1
4
o x
y
-9-
第六节
高斯公式与散度
例5 设函数
在闭区域 上具有一阶和
x v Qu y v Ru z
二阶连续偏导数, 证明格林( Green )第一公式
第 十 章
曲 线 积 分 u v u v u v ( d x d y d z 与 x x y y z z 曲 面 其中 是整个 边界面的外侧. 积 P Q R 分 分析: 高斯公式 d x d ydz x y z

S
得投影区域Dxy ,被积函数 f x , y , z 中的z换为
曲面方程z z x , y
f x, y, z x, y
f x , y , z dS S
D
xy
z z f x, y, z x, y 1 x y dxdy .
2
2
2. 若曲面S：y y( x , z )
则
S
f ( x , y , z )dS f [ x , y( x , z ), z ] 1 y x y z dxdz;
2 2 Dxz
3. 若曲面S：x x( y , z )
则
f ( x , y , z )dS S
M i i , i , i Si ,
mi f i ,i , i Si .
求和
m f i ,i , i si .
n 1

f i ,i , i si . 取极限 m lim 0
n 1

为所有小块的最大直径 .
x 2 y 2 dS
S2


D
xy
x 2 y 2 dxdy

s1 : z
x2 y2
D
1

2 0
d r rdr
2 0
1

2
1 2 2 x y dS 2 S1 S2 S



2 1 .

三、第一类曲面积分的计算
定理 设积分面S由方程z z x , y 给出, S在
xoy平面上的投影区域为Dxy , 且z z x , y

曲面积分的计算方法曲面积分是微积分中的重要概念，它在物理学、工程学和数学等领域都有着广泛的应用。

曲面积分的计算方法有多种，本文将介绍曲面积分的概念、计算方法以及相关的应用。

首先，我们来了解一下什么是曲面积分。

在数学中，曲面积分是对曲面上的某种量的积分运算。

它可以理解为对曲面上的每一点施加一个函数，并对所有点的函数值进行积分。

曲面积分分为第一类曲面积分和第二类曲面积分两种，分别对应着曲面上的标量场和矢量场。

对于第一类曲面积分，我们可以使用参数化的方法进行计算。

假设曲面S可以用参数方程。

\[。

\mathbf{r}=\mathbf{r}(u,v)。

\]来表示，其中(u,v)在一个有界区域D内变化，而函数f(x,y,z)在曲面S上有定义。

那么第一类曲面积分的计算公式为：\[。

\iint\limits_{S}f(x,y,z)\mathrm{d}S=\iint\limits_{D}f(\mathbf{r}(u,v))\left\|\frac{\partial \mathbf{r}}{\partial u} \times \frac{\partial \mathbf{r}}{\partial v}\right\|\mathrm{d}u\mathrm{d}v。

\]其中，\(\left\| \frac{\partial \mathbf{r}}{\partial u} \times \frac{\partial\mathbf{r}}{\partial v} \right\|\)表示向量\(\frac{\partial \mathbf{r}}{\partial u}\)和\(\frac{\partial \mathbf{r}}{\partial v}\)的叉乘的模长。

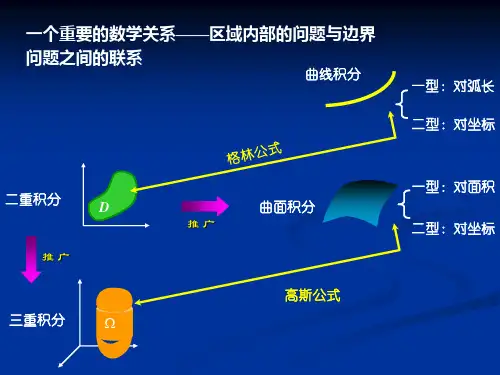
对于第二类曲面积分，常见的计算方法有高斯公式和斯托克斯公式。

高斯公式是用来计算曲面积分与曲面围成的立体的内部点相关的积分，而斯托克斯公式则是用来计算曲面积分与曲线围成的区域的内部点相关的积分。

高考数学冲刺曲面积分与高斯公式在高考数学的征程中，曲面积分与高斯公式犹如一座山峰，等待着我们去攀登。

对于许多考生来说，这部分内容可能颇具挑战性，但只要我们掌握了正确的方法和思路，就能在高考的战场上勇往直前，攻克这一难关。

首先，让我们来了解一下什么是曲面积分。

曲面积分是多元函数积分学中的一个重要概念，它包括第一型曲面积分和第二型曲面积分。

第一型曲面积分主要是计算曲面的面积，而第二型曲面积分则与向量场的通量有关。

想象一下，我们有一个曲面，就像是一个弯曲的“毯子”。

第一型曲面积分就是要计算这个“毯子”的大小，而第二型曲面积分则是要计算通过这个“毯子”的某种“流量”。

为了更好地理解曲面积分，我们需要掌握一些基本的计算公式和方法。

对于第一型曲面积分，其计算公式为：＄＼int\int_{S} f(x,y,z) dS ＝＼int\int_{D} f(x,y,z(x,y)）＼sqrt{1 ＋ z_{x}＾｛2} ＋ z_{y}＾｛2}｝dxdy$，其中$D$是曲面在$xoy$平面上的投影区域。

这里的关键是要找到曲面的方程，并求出相应的偏导数，然后进行积分计算。

而第二型曲面积分的计算则相对复杂一些。

我们需要考虑曲面的侧，通常分为上侧、下侧、左侧、右侧、前侧和后侧。

对于不同的侧，积分的正负号也会有所不同。

其计算公式为：＄＼int\int_{S} P(x,y,z)dydz ＋ Q(x,y,z) dzdx ＋ R(x,y,z) dxdy ＝＼pm ＼int\int_{D} （P ＼frac{＼partial z}｛＼partial x} ＋ Q ＼frac{＼partial z}｛＼partial y} ＋ R) dxdy$，其中“＄＼pm$”的选取取决于曲面的侧。

接下来，我们来聊聊高斯公式。

高斯公式是曲面积分中的一个重要定理，它建立了空间闭区域上的三重积分与闭区域边界上的曲面积分之间的关系。

高斯公式表述为：＄＼iiint_{＼Omega} （＼frac{＼partial P}｛＼partial x} ＋＼frac{＼partial Q}｛＼partial y} ＋＼frac{＼partial R}｛＼partial z}） dxdydz ＝＼int\int_{S} P dydz ＋ Q dzdx ＋ R dxdy$，其中$＼Omega$是空间闭区域，＄S$是闭区域$＼Omega$的边界曲面，且取外侧。

L
2
2
2
2
2
2
其中 L 是球面
2 2
x + y + z = 2bx 与柱面
2
2
2
x + y = 2 ax ( b > a > 0 ) 的交线 ( z ≥ 0 ),
从 L 正向看 L 所围球面部分总在左侧.
答案:
2bπa
2
14、求
I = ∫ ( y − z )dx + ( z − x)dy + ( x − y )dz
x + y + z − 2ax − 2ay − 2az + a = 0
其中常数 a > 0. 证明:
2
2
2
2
I =
( x + y + z − 3 a ) dS ≤ 12 π a . ∫∫
S
3
练习 5 计算
∫∫ ( x + 2 y + 3 z − 4 )
S
2
dS .
其中 S 为正八面体的表面积.
S : x
S 为平面 x = ± a , y = ± b , z = ± c
围成的长方体的全表面的外侧.求：
∫∫
S
f ( x ) dydz + g ( y ) dzdx + h ( z ) dxdy
答案:
8[bcf (a) + cag (b) + abh(c)]
注: 用高斯公式 ① P , Q , R 一阶偏导连续; ② Σ 要封闭; ③ 取外侧,否则加负号.
x + y + z = 0 的交线,从 ox 轴正向向负
向看去, L 的取向为逆时针方向.

沿场中某一有向曲面Σ的第二类曲面积分为 沿场中某一有向曲面Σ
Φ = ∫∫ A dS = ∫∫ A n 0 dS
Σ Σ
= ∫∫ Pdydz + Qdzdx + Rdxdy
Σ
向正侧穿过曲面Σ 通量. 称为向量场 A( x , y , z ) 向正侧穿过曲面Σ的通量.
散度的定义: (2). 散度的定义:
2π
1
3
9π . 2
使用Guass公式时应注意: 使用Guass公式时应注意: Guass公式时应注意
是对什么变量求偏导数; 1. P,Q, R是对什么变量求偏导数;
2.是否满足高斯公式的条件; 2.是否满足高斯公式的条件; 是否满足高斯公式的条件
3.Σ是取闭曲面的外侧. 3.Σ是取闭曲面的外侧.
Σ1 Σ1
=
h2dxdy = πh4 . ∫∫
D xy
故所求积分为
( x 2 cos α + y 2 cos β + z 2 cos γ )dS ∫∫
Σ
1 4 = πh πh4 = 1 πh4 . 2 2
物理意义: 3. 物理意义: (1). 通量的定义: (1). 通量的定义:
设有向量场
A( x , y , z ) = P ( x , y , z )i + Q ( x , y , z ) j + R( x , y , z )k
三部分组成, Σ 由 Σ 1 , Σ 2 和 Σ 3 三部分组成,
z
Σ2 Σ3
Σ1
Σ1 : z = z1( x, y) Σ2 : z = z2 ( x, y) Σ3 x
o
Dxy
y
根据三重积分的计算法
R ∫∫∫ z dv =

在包含 在内的一
证:
情形1 与平行 z 轴的直线只交于
一点;
设其方程为
为确定起见; 不妨设 取上侧 如图.
则有
则
利用格林公式
因此
同理可证
三式相加; 即得斯托克斯公式 ;
情形2 曲面 与平行 z 轴的直线交点多于一个;
则可
通过作辅助线面把 分成与z 轴只交于一点的几部分;
在每一部分上应用斯托克斯公式; 然后相加;
定义:
设有向量场
其中P; Q; R 具有连续一阶偏导数;
是场内的一片有向
则称
曲面;
其单位法向量 n,
为向量场 A 通过
有向曲面 的通量流量 .
在场中点 Mx; y; z 处
称为向量场 A 在点 M 的散度.
记作
divergence
表明该点处有正源;
表明该点处有负源;
表明该点处无源;
介于 z = 0 及
z = h 之间部分的下侧.
所围区域为;
则
利用重心公式; 注意
例3.
设 为曲面
取上侧; 求
解:
作取下侧的辅助面
用柱坐标
用极坐标
在闭区域 上具有一阶和
二阶连续偏导数; 证明格林 Green 第一公式
例4. 设函数
其中 是整个 边界面的外侧.
分析:
高斯公式
1 计算曲面积分
非闭曲面时注意添加辅助面的技巧
2 推出闭曲面积分为零的充要条件:
2. 通量与散度
设向量场
P; Q; R; 在域G内有一阶 连续
偏导数;
则
向量场通过有向曲面 的通量为

L 1
( 分别取 y 1 x 与 x 1 y )
3 4 x ) dx ( 3 4 y ) dy (
1 0
0
1
2 (34x)dx2
0
1
二. 第二型曲面积分
F (x ,y ,z) d S



[ F ( x ,y , z ) e ( x ,y , z )] d S n
P Q 6 ( x y ) 解： ( x y 0 ) 4 y x ( x y )
曲线积分在半平面 x y 0 内与路径无 .
A 到点 B . 设 L : x y 1 , 从点 1
原式 3 y x ) dx ( 3 x y ) dy (
2 2
例2 求常数 a 与 b 的值 ,使
[( xy 1 ) e ae] dx [ be (xy 1 ) e] dy
x y x y
为全微分 ,并求全微分的原函数 .
P x y 解： e ae y
Q x y be e x
P Q 由 ,得 a 1 ,b 1 y x
第十二节 第二类面积分 高斯公式 斯托克斯公式
一、平面曲线积分与路径无关的条件
(1) 设G是单连通域, F C (G ), ( x , y ) ( P ( x , y ), Q ( x , y ))
则以下四个命题等价:
C
( 1 ) 分段光滑闭曲线 C G , P d x Q d y 0 ;
( ,0 ) 2
( 0 , 0 )
( 1 2 xy y2) dx (xy )2dy
( 2,1 )
( 1 2 xy y2) dx (xy )2dy

S
(8 y 1 4 y 4 y )dV

x(8 y 1)dydz 2(1 y 2 )dzdx 4 yzdxdy
S1
dV 0 2(1 y 2 ) dzdx 0 (因为 S1 yOz, xOy 面)
S1
( y 1) dy 2( 3 2 1) dxdz

Dxy

2π 0
d 0
1
rdr
π 4

2π 0
cos 2 d
围立体 的体
积为V, 是 外法线向量与点 ( x , y , z ) 的向径
的夹角, 试证
证: 设 的单位外法向量为 则
nr cos n r
x y z cos cos cos r r r
5
例2 计算第二类曲面积分 z cos dS ，其中 S 是抛物面
S
z x y 与平面z 4 所围区域的曲面，法向取外侧.
2 2
解

S
z z cos dS dV z
4 x y
2 2
z
4
dV d

D
dz

2 0
d r dr 2 dz
1 2
2

ax dydz ( z a ) dxdy a
2 S1
2
dxdy
a 2 a 2 a 4 , 1 3 4 1 3 4 所以 原式 （ a a ） a . a 2 2
D
10
例5
利用高斯公式计算曲面积分
( x 2 cos y 2 cos z 2 cos ) dS

p
1 0 0
闭曲面外侧． 解：对第一个积分可以用高斯公式，即
is
1 ， 4
2
2 2
Ò òò
S
xy z 2 dxdy + x y 2 zdydz ，其中 S 为由曲面 z = x 2 + y 2 与平面 z = 1 所围成的
x 2 + y 2 £1 x ³ 0, y ³ 0
对于第二个积分不能用高斯公式，因为 x y z = P 在 x = 0 处偏导数不存在，只能投影，将 曲面 S 分成两块， S1 z = 1, x + y £ 1 上侧， S 2：z = x + y , 0 £ z £ 1 下侧， 因为 z = 1 垂直于 yoz 平面，所以 对于积分
第二类曲面积分计算、高斯公式
p 1 a4 = - [2p a 4 + 4p òp cos j sin j dj ] + ap a 2 a 4 2
p 3 p a + p a3 = - a3 ． 2 2 方法 2：投影法：曲面 S 投影到 yoz 平面上应分成前后两块，即
= -2p a 3 +
S前：x = a 2 - x 2 - y 2 ü ï ý 2 2 2 S后：x = - a - x - y ï þ
=
，
cos g =
2z 4x + 4 y + 4z
2 2 2
=
z x + y2 + z2
2
所以
例 4． 计算
I1 = òò xy z 2 dxdy = òòò xy
S W
= 2 òòò xy zdv = 8òòò xyzdv
W W1
nR
1 x +y

1 Φ P Q R + = lim ∫∫∫ + lim d xd yd z Ω→ M V Ω→ M V x y z
Ω Ω
M
积分中值定理
P Q R P Q R = lim + + =( + + y z ( ξ ,η , ζ ) x y z Ω→ M x
∴ I= =∑1
∫∫
1 4 1 4 4 = πh - πh = πh . 2 2
(方法2)
由对称性知 x 2 d ydz = ∫∫ y 2 d zdx = 0, ∫∫
Σ Σ
x 2 d ydz + y 2 d zdx + z 2 d xdy = ∫∫ z 2 d xdy ∫∫
Σ Σ
P Q R ( + + ) dv x y z
奇点： Σ所围闭区域 Ω上，使P, Q, R 没有 一阶连续偏导数的点.
∫∫ Pdydz + Qdzdx + Rdxdy = + ∫∫∫ –
Σ
Ω
3° 令P = x , Q = y , R = z，则
P Q R + + =3 x y z
由高斯公式可得空间立体的体积:
→
→
→
P, Q, R具有连续一阶偏导数, Σ是有向曲面片, 其单位法向量 为n, 称
Φ = ∫∫ A n d S = ∫∫ P d y d z + Q d z d x + R d x d y
Σ Σ → →
为向量场A 通过有向曲面 Σ 的通量.
(2) 背景
1o 流量
→ →
流速：A = v = { P , Q , R}
A( x, y, z) = P( x, y, z) i + Q( x, y, z) j + R( x, y, z) k

高斯(Gauss)公式通量与散度空间二维单连通域的概念：对于空间区域G,如果G内任一闭曲面所围成的区域仍属于G，则称G是空间二维单连通域;否则称G为二维复连通域.通俗而言，空间二维单连通域之中不含“洞”，而二维复连通域之中含有“洞”.例如，两个同心球面所围区域不是二维单连通域；环面（即轮胎面）所围区域是二维单连通域.一、高斯(Gauss)公式定理1设空间闭区域W 是由分片光滑的闭曲面S 所围成, 函数P (x , y , z )、Q (x , y , z )、R (x , y , z )在W 上具有一阶连续偏导数, 则有,或 其中闭曲面S 取外侧（即法方向朝外）,cos a , cos b , cos g 是S 上任一点(x ,y ,z )处法向量的方向余弦.òòòòòSW ++=¶¶+¶¶+¶¶Rdxdy Qdzdx Pdydz dv z Ry Q x P )(dS R Q P dv zRy Qx P)cos cos cos ()(òòòòòSW++=¶¶+¶¶+¶¶g b a简要证明设W 是一柱体, 上边界曲面为S 2: z =z 2(x , y ), 下边界曲面为S 1: z =z 1(x , y ), 侧面为柱面S 3, S 1取下侧, S 2取上侧; S 3取外侧. 根据三重积分的计算法, 有.另一方面, 有,,,òòòòòò¶¶=¶¶W xyD y x z y x z dz z Rdxdy dv zR ),(),(21òò-=xyD dxdyy x z y x R y x zy x R )]},(,,[)],(,,[{12òòòòS -=1)],(,,[),,(1xyD dxdy y x z y x R dxdy z y x R òòòòS =2)],(,,[),,(2xyD dxdyy x z y x R dxdy z y x R òòS =30),,(dxdy z y x R以上三式相加, 得.所以 . 类似地有, , 把以上三式两端分别相加, 即得高斯公式.òòòò-=SxyD dxdyy x z y x R y x zy x R dxdy z y x R )]},(,,[)],(,,[{),,(12òòòòòSW =¶¶dxdyz y x R dv z R ),,(òòòòòSW =¶¶dydz z y x P dv x P ),,(òòòòòSW =¶¶dzdx z y x Q dv y Q ),,(对于一般二维单连通域：对于二维复连通域：对于二维复连通域（如下图），高斯公式仍然成立:. 12()P Q Rdv Pdydz Qdzdx Rdxdy x y z W S +S +S ¶¶¶++=++¶¶¶òòòòòΣΣ1Σ2ΩGauss 公式使用要求：（1） 积分曲面å为闭曲面，取外侧；（2） å所围区域W 上函数P (x ,y,z ), Q (x ,y,z ), R (x ,y,z )有一阶连续偏导数.设空间闭区域W 是由分片光滑的闭曲面S 所围成，则闭区域W 的体积,其中闭曲面S 取外侧.13V xdydz ydzdx zdxdyS=++òò例1 利用高斯公式计算曲面积分, 其中S为柱面x 2+y 2=1及平面z =0, z =3所围成的空间闭区域W 的整个边界曲面的外侧.xdydz z y dxdy y x )()(-+-òòS解 这里P =(y -z )x , Q =0, R =x -y ,, , .由高斯公式, 有.z y x P -=¶¶0=¶¶y Q0=¶¶z R ()()x y dxdy y z xdydz S-+-òòòòòòòòWW-=-=dzd d z dxdydz z y q r r q r )sin ()(29)sin (201030p q r r r q p-=-=òòòdz z d d ΣO xyzΩ例 2 计算曲面积分, 其中S 为锥面x 2+y 2=z 2介于平面z =0及z =h (h >0)之间的部分的下侧, cos a 、cos b 、cos g 是S 上点(x , y , z )处的法向量的方向余弦. dS z y x )cos cos cos (222g b a ++òòS解 设S 1为z =h (x 2+y 2£h 2)的上侧, 则S 与S 1一起构成一个闭曲面, 记它们围成的空间闭区域为W , 由高斯公式得注意:利用对称性.1222(cos cos cos )x y z dS a b g S +S ++òò()222x y z dvW=++òòòòòò£++++=22222)(2h y x h yx dz z y x dxdy òòò£++=222222h y x h yx zdzdxdy òò£+--=222)(222h y x dxdy y x h 421hp =0)(22222=+òòò£++hy x h yx dz y x dxdy ΣO xyzΣ1而,因此 .42222222211)cos cos cos (h dxdy h dS z dS z y x h y x p g b a ===++òòòòòò£+S S 4442222121)cos cos cos (h h h dS z y x p p p g b a -=-=++òòS例3 设函数u (x , y , z )和v (x , y , z )在闭区域W 上具有一阶及二阶连续偏导数, 证明,其中S 是闭区域W 的整个边界曲面, 为函数v (x , y , z )沿S 的外法线方向的方向导数,符号, 称为拉普拉斯算子. 这个公式叫做格林第一公式. òòòòòòòòWSW¶¶¶¶+¶¶¶¶+¶¶¶¶-¶¶=D dxdydz z vz u y v y u x v x u dS n v u vdxdydz u )(n v¶¶222z y x ¶¶+¶¶+¶¶=D 证: 因为方向导数 ,其中cos a 、cos b 、cos g 是S 在点(x , y , z )处的外法线向量的方向余弦.gb a cos cos cos zv y v x v n v ¶¶+¶¶+¶¶=¶¶于是曲面积分.利用高斯公式, 即得, 将上式右端第二个积分移至左端便得所要证明的等式.òòòòSS¶¶+¶¶+¶¶=¶¶dS z vy v x v u dS n v u )cos cos cos (g b a òòS ¶¶+¶¶+¶¶=dSz v u y v u x v u ]cos )(cos )(cos )[(g b a òòòòòWS¶¶¶¶+¶¶¶¶+¶¶¶¶=¶¶dxdydz z vu z y v u y x v u x dS n v u )]()()([òòòòòòWW ¶¶¶¶+¶¶¶¶+¶¶¶¶+D =dxdydz z v z u y v y u x v x u vdxdydz u )(例4.计算曲面积分,其中S 是由曲线绕y 轴旋转一周所成的曲面,它的法向量与y 轴正向的夹角恒大于.2(81)2(1)4I y xdydz y dzdx yzdxdy S=++--òò1z y x ì=-ïí=ïî(13)y ££2p[]34p 解：这里作辅助面,法方向取右侧，则S 与S 1构成法方向指向外侧的闭曲面.记Ω为S 与S 1所围闭区域.2(81),2(1),4.P y x Q y R yz =+ =- =-81441P Q Ry y y x y z¶¶¶++=+--=¶¶¶()221:32y x z S = +£xyzOS :S 1x 2+ z 2= y-13112(81)2(1)4I y xdydz y dzdx yzdxdyS +S =++--òò12(81)2(1)4y xdydz y dzdx yzdxdyS -++--òò()2222213x z P Q R dv dzdx x y z W +£æö¶¶¶=++--ç÷¶¶¶èøòòòòò()222311162x z y dydzdx p+£-=+×òòò()231132y dy p p =-+ò()32113234.2y pp p =-+=例5.计算曲面积分，其中Σ是圆柱面被平面和所截出部分的外侧.()()222I z xy dydz x yz dxdy S=++-òò221x y +=1y z +=0z =解: 作椭圆面Σ1（取上侧）及圆面Σ2（取下侧），它们分别位于平面y +z =1及z =0上.这样Σ+Σ1+Σ2构成闭曲面，其法向量指向外侧，记Ω为Σ+Σ1+Σ2闭曲面所围空间闭区域.，因为Σ1、Σ2在yOz 坐标面上投影为零，所以，；根据高斯公式，有其中()()12222I z xy dydz x yz dxdy S +S +S =++-òò()()1222z xy dydz x yz dxdy S -++-òò()()2222z xy dydz x yz dxdyS -++-òò()1220zxy dydz S +=òò()2220z xy dydz S+=òò()I y y dv W =-òòò()()21xyD x y y dxdy ---òò()20xyD x y dxdy+-×òò()21xyxyxyD D D y y dxdy ydxdy y dxdy=-=-òòòòòò()2122200110.224xy D x y dxdy d d p p q r r r =-+=-×=-òòòò(){}22,|1.xy D x y x y =+£例6.计算曲面积分其中S 为曲面的上侧.2223()xdydz ydzdx zdxdyI x y z S++=++òò()22(2)(1)105169z x y z ---=+³[]2p 解：这里 其中，当时，，，.作辅助面上介于与之间部分，取下侧；上半球面，取下侧; 其中充分小，则S 、S 1及S 2构成法方向指向外侧的闭曲面.记Ω为S 、S 1及S 2所围空间闭区域.333,,,x y zP Q R r r r===222r x y z =++2220x y z ++¹()243351133P rx x r x r x r r -¶¶=+-=-¶¶223535113,3Q y R z y r r z r r¶¶=- =-¶¶0P Q Rx y z ¶¶¶++=¶¶¶1:0z S = 222x y d+=22(2)(1)1169x y --+=()22222:0x y z z d S ++= ³0d>xyzOSS 1S 2其中为上任意点处单位法向量.122223()xdydz ydzdx zdxdy I x y z S +S +S ++=++òò12223()xdydz ydzdx zdxdy x y z S ++-++òò22223()xdydz ydzdx zdxdyx y z S ++-++òò0P Q R dv x y z W æö¶¶¶=++-ç÷¶¶¶èøòòò23xdydz ydzdx zdxdy d S ++-òò231x y z x y z dS d d d d S éùæöæöæö=-×-+×-+×-ç÷ç÷ç÷êúèøèøèøëûòò()22222421122.x y z dS pd p d dS =++=×=òò,,x y z d d d æö---ç÷èø()22222:0x y z z d S ++= ³(),,x y z xyzOSS 1S 21.计算曲面积分,其中S 为锥面的下侧.222()()()I y z dydz z x dzdx x y dxdyS=-+-+-òò22z x y=+()0z h ££44h p éù-êúëû练习。

曲面积分与高斯公式1.第一类曲面积分(1)问题的提出设有一块光滑的金属曲面S 。

它的密度是不均匀的。

在其点(x,y ,z)s ∈处密度为f （x,y ,z ），并设f 在S 上连续,则金属曲面S 的质量M ⎰⎰=Sds z y x f ),,(说明: 第一类曲面积分与曲面的方向(侧)无关(2)第一类曲面积分的计算(代入法)设S 是一个光滑曲面， S 的方程是Z=f(x,y) ,dxdy z z y x z y x f ds z y x f Dy x s ⎰⎰⎰⎰++=221)),(,,(),,( 当 f ≡1时可得空间曲面面积的计算公式，即dxdy z z S Dy x ⎰⎰++=221例1．I=ds y x s⎰⎰+22,S 是半球面2222R z y x =++（0≥z ）。

解：222y x R z --=,222:,),(R y x D D y x ≤+∈ 222y x R x xz ---=∂∂, 222y x R y y z ---=∂∂ 22222)()(1y x R R y z x z --=∂∂+∂∂+ ⎰⎰⎰⎰⎰⎰-=--+=+πθ2002222222221R D s rdr r R r d R dxdy y x R R y x ds y x =232R π2. 第二类曲面积分(1)问题的提出磁通量问题。

表示⎰⎰∑++Rdxdy Qdzdx Pdydz说明:第二类曲面积分与方向(侧)有关，改变方向，积分变号(2)计算(代入法)⎰⎰∑++Rdxdy Qdzdx Pdydz 用带入法计算时,一般应分成三个计算: ①⎰⎰⎰⎰±=∑xyD dxdy y x z y x R dxdy z y x R )],(,,[(),,(（如果曲面积分取∑的上侧取+号，如果曲面积分取∑的下侧取-号）.类似有②⎰⎰⎰⎰±=∑xyD dydz z y z y x P dydz z y x P )],),,([(),,(（如果曲面积分取∑的前侧取+号，如果曲面积分取∑的后侧取-号）。