高思导引--四年级第二十四-逻辑推理教师版

高思学校 2013年2013高思杯“7龙珠”学习文化节综合解答及评析四年级 思维部分1、 72、3、 知识点：行程问题——火车行程．详解：齐头并进，从出发到快车完全超过慢车，两车路程差为快车车长、即火箭号长度，为()800500103000−×=米；齐尾并进，从出发到快车完全超过慢车，两车路程差为慢车车长、即精灵号长度，为()80050082400−×=米． 本题评析:齐头并进和齐尾并进是火车行程问题中的两种基本类型．解决火车行程问题，最关键的就是要学会画图，找到整个行程过程中两车的路程与车长的关系．高思学校 2013年二、计算题4、 答案：201300000知识点：计算问题——乘法凑整．详解：()()1253225201312584252013201300000×××=××××= 5、 答案：5100知识点：计算问题——提取公因数．详解：()475151535147535100×+×=×+= 6、 答案：213213知识点：计算问题——凑整&叠数．详解：()10012131000121321310002131213213×=+×=×+×= 7、 答案：20127987知识点：计算问题——凑整．详解：()9999201310000120132013100002013120127987×=−×=×−×= 8、 答案：20知识点：计算问题——带符号搬家．详解：()()3673593693574520÷×÷=÷×÷=×= 9、 答案：6知识点：计算问题——整除详解：()()1815451815951891556×÷=×÷÷=÷×÷= 10、 答案：4.63知识点：计算问题——小数加法详解：6.7 1.83 3.98.53 3.9 4.63+−=−= 11、 答案：1知识点：计算问题——小数乘法 详解：2.50.41×= 12、 答案：1.2知识点：计算问题——小数除法详解：除以10，小数点往左移一位：1210 1.2÷=高思学校 2013年13、 答案：128.9知识点：计算问题——小数点移动、提取公因数详解：12.89 6.37 1.28936.312.89 6.3712.89 3.63×+×=×+× ()12.89 6.37 3.6312.8910128.9×+×三、填空题I本题评析:本题也可以直接用三阶幻方性质解决，任意过中心格的三个数均成等差数列，所以左上角的数为16、左下角的数为21、第一行中间数为25，其他格依次可填出．高思学校 2013年19、 答案：3知识点：计算问题——定义新运算．详解：☺9 =3，☺16 = 4，☺25 = 5，可以找到规律：结果数的平方等于笑脸后的数．☺(☺81)，先算括号中的☺81 = 9，☺9 = 3． 20、 答案：21知识点：行程问题——火车行程．（2）秘钥改为“3倍多2”．高：G 明码6、密码63220×+=；A 明码0、密码03202×+=；O 明码14、密码143244×+=；所以“高”密码为200244．思：S 明码18、密码183256×+=；I 明码8、密码83226×+=；所以“思”密码为5626． 杯：B 明码1、密码13205×+=；E 明码4、密码43214×+=；I 明码8、密码83226×+=；所以“杯”密码为051426．高思学校 2013年六、填空题II23、 答案：80知识点：和差倍——比较法 详解：① 10天的工资是2个高思币加1个水晶币，也可以是每天获得20个紫云币、即10天共200个紫云币；可得21200×+××高水紫；② 10天的工资是2个高思币加1个水晶币，所以40天的工资就应该是其4倍，即8个高思币1一共有 而每个老师负责的两色手环必须是连续的，所以常荣老师一定负责蓝和白．接下来可确定董一定是负责黄和橙；尹博一定负责红和绿，所以负责紫色手环的一定是谷高思学校 2013年佛老师：26、 答案：48详解：首先，观察竖式中的减法，可得“人=0”，即“哈×皮=___0”；“哈哈×哈=欢快节”，所以可得“哈”不可能是1、2、3、5、6，因此可得“皮”一定是5，“哈”是偶数，即只能是4或8；然后“哈”分别试一下4和8，可得答案，“哈”为4，“皮”为5，“愚”为2，“人”为0，“欢”为1，“乐”为3，“快”为7，“节”为6． 28、 答案：71乐 乐高思学校 2013年知识点：计数——加乘原理、排列组合、枚举． 详解：分两步考虑：先考虑名师PK 、高思杯、诊断这三个活动，用“√”表示参加、“×”表示不参加，先后共有√√√、√××、×××三种可能；再考虑猜灯谜、口述题大赛、漫画show 、在线寻龙这四个活动，分别有3（0个、1个或2个手环）、2（0个或1个手环）、2、2种可能，所以这四个活动共有322224×××=种可能； 所以七项活动获得龙珠环的情况共有32472×=种不同的可能；30、 答案：（1）10；（2）见详解．知识点： 详解：（1）画出行程线段图：图中虚线部分长度就是两段实线的路程差，原与400秒400秒100秒原 后高思学校 2013年后速度差为2米/秒，时间为400秒，所以路程差等于2400800×=米； 即哈利冒雨飞行100秒的路程就是800米，冒雨飞行速度为800÷100=8米/秒； 所以，哈利预计飞行速度为8210+=米/秒． 答：哈利的预计飞行速度是每秒钟10米．（2）第（1）问中，哈利冒雨飞行的速度是： 8 （米/秒）； 哈利从队尾飞到队头，他与队伍的路程差为队伍长度；43====① 3个人握手次数少于9：A 与B 没握、A 与C 没握； ② 4个人握手次数少于9：A 与B 没握、C 与D 没握． 答：握手次数少于9的可能有3个人，也可能有4个人．。

学习-----好资料第5讲竖式问题内容概述以字母或汉字表示数字的竖式问题，学会选择适当的突破口，并逐步解决问题；能够将文字叙述的题目转化为数字谜形式，便于直观地解决问题。

典型问题兴趣篇1.如图5-1所示，每个英文字母代表一个数字，不同的字母代表不同的数字，其中“G”代表“5”，“A”代表“9”，“D”代表“0”，“H”代表“6”.问：“I”代表的数字是多少？分析：也一定有A+E=HC=4，A+D=D，所以,它们的和一定有进位，所以，、2、F分别是1没有用，所以1、2、3、8B，现在还剩进位，所以E=7I=3.的加法竖式中，不同的汉字代表不同的数字，相同的汉字代）在图5-22. （1 表相同的数字，那么每个汉字各代表什么数字？的减法竖式中，不同的汉字代表不同的数字，相同的汉字代表相在图5-3(2)同的数字，那么每个汉字各代表什么数字？分析：，卒=1（1）观察可得：车，马=卒，所以兵=5=0，兵+兵马，所炮=，+1=5，所以马=4炮+=2以炮5240+5210=10450=2=马，所以：兵，=12）观察可得：炮，兵—兵=马，一定有借位，所以马=9，炮—兵（292=929—1221的竖式中，相同的汉字代表相同的3. 在图5-4+如果23+解数字，不同的汉字代表不同的数字，”所代表的三，那么“字++谜=30 数数字谜位数是多少？更多精品文档．学习-----好资料不同的汉字代表不同的数字，每个汉字代表一个数字，图5-5所示的竖式中，4. ”代表的四位数是多少？那么“北京奥运分析：奥++京，北+奥=0，所以可得要进位，所以；京=8 观察可得：北=1，北+京=9 ，运位，所以：奥=0+运=8，所以要进2=1809 北京奥运ABCDE所示的乘法竖式成立，那么5. 已知图5-6是多少？相同的符号代5-7的竖式中，6. (1) 在图表相同的数字，不同的符号代表不同的数字，那么☆、△、○分别代表什么数字？的竖式中，相同的符号代表5-8(2) 在图不同的符号代表不同的数字，相同的数字，那么☆、△、○分别代表什么数字？分析：三种可能，因为是三位数5、9,×△=△，所以△=1、）（1△，○=1，☆乘一位数等于四位数，所以1排除，经分析：△=5=2=2 ，○，当△=5时，☆=4、）△=15、6三种可能，排除12 （=3○=5时，△当=6☆，更多精品文档．学习-----好资料7. 如图5-9，相同的字母表示相同的数字，不同的字母表示不同的数字，那么十个方框中数字之和是多少？分析：B×B=B，所以B=1、5、6，三种可能，经分析1排除，A×B=B，所以B=5，A为奇数，三位数乘B得三位数，所以第一个方格中添1，一百多乘一位数得四位数，所以A只能是7、9，当A=7时，C=7，矛盾不成立；当A=9时，C=7，成立；所以：195×95=18525 1+9+1+7+5+1+8+5+2+5=448. 在图5-10和图5-11中的方格内填入适当的数字，使下列除法竖式成立.分析：，所以除数9=783（1）除数×=6003 ，所以被除数×6=522=87,8787=69÷6003=2465 5=145，所以被除数8=232，所以除数=29,29×（2）除数×29=85÷2465所示的除法竖式中填入合适的数字，使得竖式成立，那么其中的商5-129.在图是多少？分析：三= 除数×7=两位数，除数×另一个一位数，所以除数只能是位数，且三位数的十位上是2 ，9=12614,14×7=98,14×=79所以除数更多精品文档．好资料学习-----后所得乘积恰好是将原来的四位数各位数字顺序910. 有一个四位数，它乘以.颠倒而得的新四位数，求原来的四位数拓展篇不同的汉字代表不同的数字，相同的汉字代表相同的数字，和5-14中，1. 在图5-13. 求出它们使竖式成立的值分析：，四个语、语=5 （1）观察得：巧=1，所以三个英相加得数，进2相加得20，所，向前进2的个位是8，所以英得6 以学=4 以学+学得数个位也是8，所1465+林=7，奥++=6，奥林+匹进2，所以林2 （）观察的奥+林有进1，所以奥6789=83，所以匹，克=9 匹+克进，在这个算式中，相2. 如图5-15不同的同的字母代表相同的数字，、A字母代表不同的数字，那么数字分别是多少？B、C分析：有借位，没有借位，C—BCA=A，—B=B,所以C—AC观察—A=4A=A，所以B=9，所以有借位且，C=8，已知C—B—B=B8、4、9不同的字母表示不同的数在图5-16的竖式中，相同的字母表示相同的数字，3. 字，并且A<B<C<D. 问：竖式中的和是多少？分析：D=5 C=4，，，观察得A=2B=3 2233+3344+4455=10032更多精品文档．学习-----好资料4. 在图5-17的竖式中，相同的汉字表示相同的数字，不同的汉字表示不同的数字，那么“”所代表的七位数是多少？携手上海世博会分析：，个=9，手=0，上观察得，黄金三角：携=1，所=7位数的和肯定要进位，要使进1为，则博，=6位，办海=4，假设百位向前进2以会只能是2，，位，办=5，成立，1094382 ；假设百位向前进3=8当世=3时，在；，成立，1094872=8时，在=3当世小悦写了一个四位数，冬冬把这个四位数的个位抹掉，变成了一个三位数，5. 阿奇又把这个三位数的个位抹掉，变成了一个两位数，最后把这三个数加起来，小悦原来写的四位数是多少？结果刚好是7826.分析：利用位值原理ABCD+ABC+AB=78261000A+100B+10C+D+100A+10B+C+10A+B=1110A+111B+11C+D=7826D=1 56-55=1 则当则B=0 C=5时－时当A=778267770=56 7051即一个各位数字互不相同的三位数，用它的三个数字组成一个最大的三位数，6. 再用这三个数字组成一个最小的三位数，组成的这两个三位数之差正好是原来. 求原来的三位数的三位数.更多精品文档．学习-----好资料移到左边首位数字前面，所构成44，将这个7. (1) 一个自然数的个位数字是 4倍，那么原数最小是多少？的新数恰好是原数的一个五位数，将它的各位数字顺序颠倒就可以得到一个新的五位数，而且(2)/4倍，那么原来的五位数是多少这个新的五位数恰好是原数的）（1219782）（中的一个数字，不同的字母2，……908. 如图5-18，每一个英文字母代表，1 、RF分别代表什么数字？、、、代表不同的数字，则字母AQT更多精品文档．学习-----好资料分析：不QAQ×T=1符合题意，当Q=6时为5或6 当Q=5时A=2 .........QTAQ等于T=1 则........AQ×T=AQF=3R=7，Q=5，T=1，A=2，所以“美”三个汉字分别代表三个各不相同的“峡”、中的竖式里，“江”、9. 图5-19. 数字，请把这个竖式写出来分析：=6 ，所以美0,1,5,6中的一个，通过实验排除0,1,5先确定美是□□江，则=×江4或8之一，又因为江峡美或美通过确定江是2 排除，所以江=24或8=8=□□□峡，则峡由于江峡美×峡所示的除法5-2010. 请把如图竖式中空缺的数字补上，其中的商是多少？分析：1 7 则除数个位是7，商的十位数字是=6.........6□□×□□除数的十位数3=×□□□61 则商的个位数字是，7.........6□8 字是更多精品文档．学习-----好资料11. 请把图5-21中的除法竖式补充完整。

第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题，处理多个对象时可采用列表的形式，在年龄问题中，通常采用和差倍问题的分析方法，有时需注意任意两人的年龄差保持不变。

典型问题兴趣篇1. 某数加上6，再乘以6，再减去6，再除以6，其结果等于6，则这个数是多少？答案：这个数是详解：+6 x6 -6 +662. 有一个人非常喜欢喝酒，他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦，看到一个酒店就把酒葫芦中的酒加一倍，然后喝下8两酒，这天他一共遇到3家酒店，在最后一家酒店喝完酒后，葫芦里的酒刚好喝完. 问：原来酒葫芦里有多少两酒？答案：7两酒。

详解：每经过一个酒店，葫芦里酒的数量就先乘2，再减8，利用倒推法，我们反过来应该先加8，再除以2.那么到酒店C之前葫芦里应该有（0+8）÷2=4两酒，他在到酒店B的时候应该有（4+8）÷2=6两酒，所以他原来的酒葫芦应该有（6+8）÷2=7两酒。

0+8=8，8÷2=4，4+8=12，12÷2=6，6+8=14，14÷2=73. 某人发现了一条魔道，下面有一个存钱的小箱子，当他从魔道走过去的时候，箱子里的一些钱会飞到人的身上使人身上的钱增加一倍，这人很高兴；当他从魔道走回来时，身上的钱会飞到箱子里，使箱子里的钱增加一倍；这人一连走了3个来回后，箱子里的钱和人身上的钱都是64枚一元的硬币，那么原来这人身上有多少元？箱子里有多少元？答案：原来这个人身上有43元，箱子里有85元。

详解：4. 三棵树上共有48只鸟. 后来，第一棵树上有一半的鸟飞到了第二棵树上；之后，第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上；最后，第三棵树上又有10只鸟飞到了第一棵树上，此时三棵树上的鸟一样多. 问：一开始三棵树上各有几只鸟？答案：第一棵树上有12，第二棵23，第三棵13详解：5. 1997年张伯伯45岁，小方9岁，在哪一年张伯伯的年龄是小方年龄的4倍？答案：小方12岁那年。

第24讲逻辑推理一内容概述简单的逻辑推理问题，学会假设法和列表法.典型问题兴趣篇1．甲、乙、丙三人中有一人是牧师，有一人是骗子，还有一人是赌棍．牧师从不说谎，骗子总说谎，赌棍有时说真话有时说谎话．甲说：“我是牧师．”乙说：“我是骗子．”丙说：“我是赌棍．”请问：甲、乙、丙三人中谁是牧师?谁是骗子?谁是赌棍?2．有三只盒子，一只盒子里装有两个黑球，另一只盒子装有两个白球，还有一只盒子里装有黑球和白球各一个．现在三只盒子上的标签全贴错了．你能否仅从其中一只盒子里拿出一个球来，就确定这三只盒子里各装的是什么球?3．费叔叔手里握有两个硬币，他让小悦、冬冬和阿奇猜哪只手握有硬币．小悦说：“左手没有，右手有．”冬冬说：“右手没有，左手有．”阿奇说：“不会两手都没有，我猜左手没有．”结果三个人的话都说对一句，说错一句．请问：费叔叔是怎么握住硬币的?4. 甲、乙、丙、丁四位同学的运动衫上印上了不同的号码：赵说：“甲是2号，乙是3号．”钱说：“丙是4号，乙是2号．”孙说：“丁是2号，丙是3号．”李说：“丁是1号，乙是3号．”又知道赵、钱、孙、李每人都只说对了一半．请问：丙的号码是几号?5．A、B、C、D四人在争论今天是星期几．A说：“明天是星期五．”B说：“昨天是星期日．”C说：“你们俩说的都不对．”D说：“今天不是星期六．”实际上这四人中只有一人说对了．请问：今天是星期几?6．爱丽丝梦游仙境时，误入一片魔法森林——健忘森林．在森林中徘徊了很久以后，爱丽丝很想知道今天是星期几．这时她刚巧碰到了老山羊．爱丽丝赶忙问它：“请问您知道今天是星期几吗?”老山羊回答说：“真糟糕，我也不记得了!不过，你可以去问问狮子和独角兽．狮钢在星期一、二、三是说谎的；独角兽在星期四、五、六是说谎的；其余的日子，它们利会说真话．”于是，爱丽丝就去找狮子和独角兽，并问它们今天是星期几．独角兽回答说：“昨天是我说谎的日子．”狮子也回答说：“昨天是我说谎的日子．”请你帮爱丽丝想一想，今天到底是星期几呢?7. 甲、乙、丙三位老师分别教四年级三班的语文、数学和英语．已知：甲老师不教英语；英语老师是一个学生的哥哥；丙是一位女老师，她比数学老师活泼．请问：乙老师教什么课?8．甲、乙、丙、丁四名同学同在一间教室里．他们当中一个人在做数学题，一个人在念英语，一个人在看小说，一个人在写信．已知：①甲不在念英语，也不在看小说；②如果甲不在做数学题，那么丁不在念英语；③有人说乙在做数学题，或在念英语，但事实并非如此；④丙既不是在看小说，也不在念英语．请问：在写信的是谁?9. 小悦、冬冬、阿奇去参加一次奥运活动．他们三人分别戴着三种不同颜色的帽子，穿着三种不同颜色的衣服．已知：①帽子和衣服的颜色都只有红、黄、蓝三种；②小悦没戴红帽子，冬冬没戴黄帽子；③戴红帽子的那个人没有穿蓝衣服；④戴黄帽子的那个人穿着红衣服；⑤冬冬没有穿黄色衣服．请问：小悦、冬冬、阿奇各戴什么颜色的帽子，穿什么颜色的衣服?10. 甲、乙、丙、丁、戊五人各从图书馆借来一本小说，他们约定读完后互相交换．这五本书的厚度以及他们五人的阅读速度都差不多，因此五人总是同时交换书．经过数次交换后，他们都读完了这五本书．已知：①甲最后读的书是乙读的第二本；②丙最后读的书是乙读的第四本；③丙读的第二本书甲在一开始就读了；④丁最后读的书是丙读的第三本；⑤乙读的第四本是戊读的第三本；⑥丁第三次读的书是丙～开始读的那本．设甲、乙、丙、丁、戊五个人最后读的书分别为A、B、C、D、E，请根据以上条件确定这五个人读的第四本书分别是什么?拓展篇1. 甲、乙、丙三人中有一人是牧师，有一人是骗子，还有一人是赌棍．牧师从不说谎，骗子总说谎，赌棍有时说真话有时说谎话．甲说：“丙是牧师．”乙说：“甲是赌棍”丙说：“乙是骗子．”请问：甲、乙、丙三人中谁是牧师?谁是骗子?谁是赌棍?2. 期末考试结束后，甲、乙、丙、丁四名同学在一起议论．甲说：“自然成绩第一名是丁.”乙说：“数学成绩第一名是丙．”丙说：“语文成绩第一名不是甲．”丁说：“英语成绩第一名是乙．”成绩公布后发现，这四名同学确实分别取得了语文、数学、英语、自然的第一名，但只有取得语文和自然第一名的学生做出的猜测是正确的．请问：数学成绩第一名是谁?3．甲、乙、丙、丁四人对A先生的藏书数目作了一个估计．甲说：“A先生有500本书．”乙说：“A先生至少有1000本书．”丙说：“A先生的书不到2000本．”丁说：“A先生最少有1本书．”实际上这四个人的估计中只有一句是对的．问：A先生究竟有多少本书?4．法官在审理一起盗窃案的过程中，对四名犯罪嫌疑人甲、乙、丙、丁进行审问．甲说：“罪犯在乙、丙、丁三人之中．”乙说：“我没有作案，是丙偷的．”丙说：“甲、丁之中有一个是罪犯．”丁说：“乙说的是事实．”如果这四个人中有两人说的是真话，另外两人说了假话，而且只有一个罪犯．请你判断：罪犯是谁?5．某参观团根据下列条件从A、B、C、D、E这五个地方中挑选参观地点：①若去A地，则必须去B地；②B、C两地中至多去一地；③D、E两地中至少去一地；④C、D两地都去或者都不去；⑤若去E地，一定要去A、D两地．请问：参观团所去的地点有哪些?6．某校数学竞赛，A、B、C、D、E、F、G、月这8位同学获得前八名．老师让他们猜一下谁是第一名．A 说：“F或者H是第一名．”B说：“我是第一名．”C说：“G是第一名．”D说：“B不是第一名．”E说：“A 说得不对．”F说：“我不是第一名，H也不是第一名．”G说：“C不是第一名．”H说：“我同意A的意见．”老师指出：8个人中有3人猜对了．问：第一名是谁?7．徐、王、陈、赵四位师傅分别是工厂的木工、车工、电工和钳工，他们都是象棋迷．已知：①木工只和车工下棋，而且总是输给车工；②王、陈两位师傅和木工经常一起看球；③陈师傅与电工下棋互有胜负；④徐师傅比赵师傅下的好．问：徐、王、陈、赵四位师傅各是什么工种?8．甲、乙、丙、丁四个人中有教师、医生、律师、警察各一名．已知：①教师不知道甲的职业；②医生曾给乙治过病；③律师是丙的法律顾问；④丁不是律师；⑤乙和丙从未见过面．请你根据上面的条件判断甲、乙、丙、丁的职业分别是什么?9．有三户人家，父亲分别姓王、张、陈，母亲分别姓刘、李、胡，每家一个孩子，分别叫明明(女)、宁宁(女)、松松(男)．已知：①王爸爸和李妈妈的孩子都参加了女子体操队；②张爸爸的女儿不叫宁宁；③陈和胡不是一家．请问：哪些人是一家?10．甲、乙、丙、丁四位老师各教两门不同的课．已知：①甲在星期二没课；②乙在星期一不给一班上课；③丙星期二前两节都有课；④物理老师星期一前两节没课．请你根据上面的课程表判断他们各教哪两门课．11．甲、乙两校举行象棋比赛．两校各选五名选手进行循环赛，即每名选手都与对方五名选手各赛一盘，每天赛五场，共赛五天．甲校的五名选手是丁一、胡二、张三、李四、王五．已知：①丁一第一天的对手第二天与胡二相遇；②第三天被李四打败的选手第四天胜了王五：③王五第四天的对手第五天与胡---T成和棋；④第五天胜了张三的选手第三天败给胡二；⑤王五第二天的对手最后一天与丁一对阵．请问：第三天与丁一比赛的选手，最后一天与谁比赛?12. 在国际饭店的宴会桌旁，甲、乙、丙、丁4位朋友进行有趣的交谈．他们分别用了汉语、英语、法语、日语4种语言．并且还知道：①甲、乙、丙各会两种语言，丁只会一种语言；②有一种语言4人中有3人都会；③甲会日语，丁不会日语，乙不会英语；④甲与丙、丙与丁不能直接交谈，乙与丙可以直接交谈；⑤没有人既会日语，又会法语．请根据上面的条件，判断他们各会什么语言．超越篇1．如图24-1所示，8张相同大小的正方形纸片摆放在桌子上，其中正方形纸片A可以完全看到，其他7张正方形纸片由于互相重叠而只露出一部分．这些纸片从上到下的摆放次序是怎样的?2．五年级有四个班，每个班有两个班长，召开年级班长会议时每班都有一名班长参加．参加第一次会议的是A、B、C、D；参加第二次会议的是B、D、E、F；参加第三次会议的是A、B、E、G．又已知日三次会议都没参加．请问：和A、B、C、D同班的分别是谁?3．赛马比赛前，五位观众给A、B、C、D、E五匹赛马预测名次．甲说：“B第三，C第五．”乙说：“E 第四，D第五．”丙说：“A第一，E第四．”丁说：“C第一，B第二．”戊说：“A第三，D第四．”结果每个名次都有人猜中，请求出各匹马的名次．4．房问里有12个人，其中有些人总说假话，其余的人总说真话．其中一个人说：“这里没有一个老实人．”第二个人说：“这里至多有一个老实人．”第三个人说：“这里至多有两个老实人．”如此往下，至第十二个人说：“这里至多有11个老实人．”请问：房间里究竟有多少个老实人?5．在一列国际列车上，有A、B、C、D四位不同国籍的旅客，他们分别穿蓝、黑、灰、褐色的大衣，坐在一张桌子的两边．桌子每边坐两个人，而且他们正好与另一边的某人面对面．已知：①英国旅客坐在B先生左侧；②A先生穿褐色大衣；③穿黑色大衣的坐在德国旅客右侧；④D先生的对面坐着美国旅客；⑤俄国旅客穿着灰色大衣．问：A、B、C、D分别是哪国人?分别穿什么颜色的大衣?6. A、B、C、D四人分别到甲、乙、丙、丁四个单位办事．已知甲单位星期一不接待，乙单位星期三不接待，丙单位星期四不接待，丁单位只在星期二、四、六接待，星期日四个单位都不办公．一天，他们议论起哪天去办事A说：“你们可别像我前天那样，在人家不接待的日子去．”B说：“我今天必须去，明天人家就不接待了．”C说：“我和B正相反，今天不能去，明天去．”D说：“我从今天起，连着四天哪天去都行．”问：这天是星期几?他们分别去哪个单位办事?7. 一次羽毛球邀请赛，来自湖北、广东、福建、北京和上海的五名运动员相遇在一起，据了解：①李平仅和另外两名运动员比赛过；②上海运动员和另外三名运动员比赛过；③陈兵和广东运动员是好朋友，但他们从未比赛过；④福建运动员和林华比赛过；⑤赵新仅与一名运动员比赛过；⑥广东、福建、北京的三名运动员都相互交过手．请问：张强是哪个省／市的运动员?8. 有甲、乙、丙、丁、戊五个人，每个人都非常有特点，他们来自不同的城市，开不同品牌的车子，喝不同种类的茶，穿不同颜色的衬衫．一次聚会上他们遇到一起，把车从左到右排成了一行．已知：①甲开奔驰；②乙穿绿衬衫；③丙喝碧螺春；④宝马车紧挨在奥迪车的左边；⑤宝马车的主人喝铁观音；⑥北京人穿蓝衬衫；⑦丰田主人来自天津；⑧中问那辆车的主人喝龙井茶；⑨丁的车在最左边；⑩上海人的车在穿红衬衫人的车旁边；⑾穿白衬衫人的车在天津人的车旁；⑿广州人喝菊花茶；⒀戊是重庆人；⒁丁的车在别克车的旁边；⒂上海人的车挨着喝乌龙茶的人的车．请问：谁穿黑衬衫?他是哪里人?他开什么车?喝什么茶?第24讲逻辑推理一兴趣篇1．甲、乙、丙三人中有一人是牧师，有一人是骗子，还有一人是赌棍．牧师从不说谎，骗子总说谎，赌棍有时说真话有时说谎话．甲说：“我是牧师．”乙说：“我是骗子．”丙说：“我是赌棍．”请问：甲、乙、丙三人中谁是牧师?谁是骗子?谁是赌棍?答；甲是牧师，乙是赌棍，丙是骗子。

⾼思数学-各级别全年教材⼤纲三年级上第1讲加减法巧算第2讲基本应⽤题第3讲间隔问题第4讲简单枚举第5讲字典排列法与树形图法第6讲找规律第7讲和倍问题与差倍问题第8讲和差问题与多个对象的和差倍第9讲简单加减法竖式第10讲周期问题初步第11讲周期问题进阶第12讲妙⽤假设法第13讲分组与画图第14讲等差数列初步第15讲等差数列进阶第16讲平⾯图形认知第17讲⽴体图形认知第18讲基本盈亏问题第19讲智巧趣题⼀第20讲旅⾏中的数学三年级下第⼀讲乘除法巧算第⼆讲归⼀问题第三讲分类计数第四讲和差倍问题中的隐藏条件第五讲线段图解复杂和差倍关系第六讲简单乘法竖式第七讲简单除法竖式第⼋讲假设法综合提⾼第九讲分组法综合提⾼第⼗讲四则混合运算第⼗⼀讲阵列问题第⼗⼆讲巧填算符第⼗三讲算符与数字第⼗四讲盈亏条件的转化第⼗五讲复杂盈亏问题第⼗六讲长度计算第⼗七讲⾓度的计算第⼗⼋讲找位置第⼗九讲⽕柴棍算式与⽣活趣题第⼆⼗讲三年级期末复习与检测四年级上第1讲整数计算综合第2讲还原问题第3讲数阵图初步第4讲竖式问题第5讲⼏何图形剪拼第6讲路程、时间、速度第7讲⾏程中的线段图第8讲简单抽屉原理第9讲基本直线形⾯积公式第10讲底、⾼的选取与组合第11讲变倍问题第12讲和差倍中的分组⽐较第13讲年龄问题第14讲数列数表规律第15讲复杂数表估算第16讲加法原理与乘法原理第17讲乘法原理进阶第18讲⽕车⾏程第19讲统筹规划第20讲游戏对策四年级下第1讲⼩数的运算技巧第2讲多位数巧算第3讲简单平均数第4讲多组对象的平均数第5讲复杂竖式第6讲横式问题第7讲格点图形的计算第8讲割补法巧算⾯积第9讲多⼈多次的相遇与追及第10讲排列组合公式第11讲排列组合应⽤第12讲分段计算的⾏程问题第13讲多次往返相遇与追及第14讲从洛书到幻⽅第15讲复杂数阵图第16讲有特殊要求的挑选第17讲捆绑法与插空法第18讲最值问题第19讲逻辑推理第20讲四年级期末复习与检测五年级上第1讲分数计算与⽐较⼤⼩第2讲整除问题初步第3讲整除问题进阶第4讲质数与合数第5讲容斥原理第6讲流⽔⾏船问题第7讲环形路线问题第8讲⽜吃草问题第9讲⼏何计数第10讲约数、倍数初步第11讲约数与倍数进阶第12讲分数与循环⼩数第13讲⽐较与估算第14讲数论巧解数字谜第15讲包含分数、⼩数的数字谜第16讲分数应⽤题之量率对应第17讲分数应⽤题之单位“1”的转化第18讲巧解不确定性问题第19讲倍数关系求解直线形第20讲巧连辅助线解直线形五年级下第1讲计算综合第2讲分数裂项第3讲圆与扇形初步第4讲圆与扇形中的重叠与旋转第5讲余数的性质与计算第6讲物不知数与同余第7讲复杂抽屉原理第8讲⼯程问题初步第9讲⼯程问题进阶第10讲钟表问题第11讲⽐例关系求解直线形第12讲平⾏线相关⽐例与勾股定理第13讲构造论证第14讲⾏程问题中的变速问题第15讲⾏程问题中分段与⽐较第16讲位值原理第17讲数字问题第18讲数论相关的计数第19讲数字谜中的计数第20讲五年级期末复习与检测六年级上第1讲计算综合⼆第2讲⽐例计算与列表分析第3讲正反⽐例的概念与应⽤第4讲⽅程解应⽤题第5讲浓度问题第6讲经济问题第7讲逻辑推理⼆第8讲最值问题⼆第9讲不定⽅程第10讲⽴体⼏何第11讲复杂直线形计算第12讲⼏何综合问题第13讲递推计数第14讲对应计数第15讲⾏程问题中的⽐例关系第16讲复杂⾏程问题选讲第17讲数论综合与简单代数式第18讲数字谜综合⼆第19讲应⽤题综合⼀第20讲应⽤题综合⼆六年级下第1讲构造论证⼆第2讲进位制与取整符号第3讲计数综合提⾼第4讲数论与⽅程第5讲计算综合练习第6讲⼏何综合练习第7讲应⽤题综合练习第8讲数字谜综合练习第9讲数论综合练习第10讲计数综合练习第11讲组合综合练习第12讲⼩升初总复习模拟测试第13讲⼩升初总复习模拟测试⼆第14讲⼩升初总复习模拟测试三第15讲⼩升初总复习模拟测试四第16讲⼩升初总复习模拟测试五第17讲⼩升初总复习模拟测试六第18讲⼩升初总复习模拟测试七第19讲⼩升初总复习模拟测试⼋第20讲⼩升初总复习模拟测试九。

学习-----好资料第4讲数阵图初步内容概述各种较为基本的数阵图问题，了解重数的概念，并以此进行分析；学会分析特殊位置上的数值；某些情况下还需要考虑对称性。

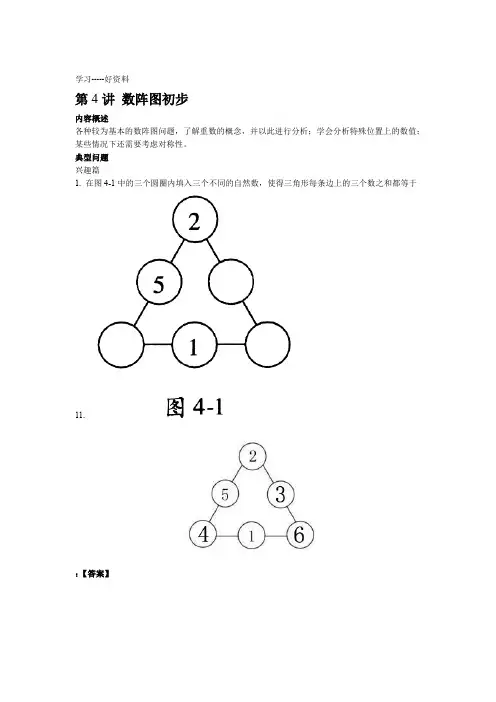
典型问题兴趣篇1. 在图4-1中的三个圆圈内填入三个不同的自然数，使得三角形每条边上的三个数之和都等于11.：【答案】【分析与解】：先如下图将空白处标上字母：根据题意：a＝11－2－5＝4；b＝11－4－1＝6；c＝11－2－6＝3.2. 请分别将1，2，4，6这四个数填在图4-2中的各空白区域内，使得每个圆圈里四个数之和都等于15.更多精品文档．学习-----好资料：【答案】【分析与解】：如下图，先将空白区域标上字母根据题意：上面圆内四个数之和等于15，可得a＋d＝15－5－7＝3＝1＋2；同理，b＋d＝15－5－3＝7＝1＋6；c＋d＝15－7－3＝5＝1＋4。

由于d属于三个圆的公共部分，经对比发现可得：d＝1；a＝2；b＝6；c＝4.3. 如图4-3所示，请在三个空白圆圈内填入三个数，使得每条直线上三个数之和都相等。

：【答案】【分析与解】：如下图：因为8＋9＋a＝b＋a＋7可得b＝10；那么每条线的和＝8＋3＋10＝21；那么a＝21－8－9＝4；c ＝21－8－7＝6.4. 把1至8分别填入图4-4的八个方格内，使得各列上两个数之和都相等，各行四个数之更多精品文档．学习-----好资料和也相等。

【答案】：1 7 6 45283【分析与解】：因为1＋2＋3＋……＋8＝36；所以每行的和等于36÷2＝18；每列的和＝36÷4＝9；从列入手，可将1~8这八个数分为和等于9的四组：1＋8＝2＋7＝3＋6＝4＋5。

再调整使行和等于18：我们发现1＋4＝2＋3；8＋5＝6＋7.经过调整可得答案。

5. 把1至12分别填入图4-5的圆圈内，使图中三个小三角形三条边上的六个数之和相等。

【答案】：【分析与解】：经过观察发现，此图是个具有对称性的图案；若使三个小三角形的三边之和相等；只需要使得图中每条边上的两个数之和相等即可。

第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题，处理多个对象时可采用列表的形式，在年龄问题中，通常采用和差倍问题的分析方法，有时需注意任意两人的年龄差保持不变。

典型问题兴趣篇1. 某数加上6，再乘以6，再减去6，再除以6，其结果等于6，则这个数是多少？答案：这个数是详解：+6 x6 -6 +662. 有一个人非常喜欢喝酒，他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦，看到一个酒店就把酒葫芦中的酒加一倍，然后喝下8两酒，这天他一共遇到3家酒店，在最后一家酒店喝完酒后，葫芦里的酒刚好喝完. 问：原来酒葫芦里有多少两酒？答案：7两酒。

详解：每经过一个酒店，葫芦里酒的数量就先乘2，再减8，利用倒推法，我们反过来应该先加8，再除以2.那么到酒店C之前葫芦里应该有（0+8）÷2=4两酒，他在到酒店B的时候应该有（4+8）÷2=6两酒，所以他原来的酒葫芦应该有（6+8）÷2=7两酒。

0+8=8，8÷2=4，4+8=12，12÷2=6，6+8=14，14÷2=73. 某人发现了一条魔道，下面有一个存钱的小箱子，当他从魔道走过去的时候，箱子里的一些钱会飞到人的身上使人身上的钱增加一倍，这人很高兴；当他从魔道走回来时，身上的钱会飞到箱子里，使箱子里的钱增加一倍；这人一连走了3个来回后，箱子里的钱和人身上的钱都是64枚一元的硬币，那么原来这人身上有多少元？箱子里有多少元？答案：原来这个人身上有43元，箱子里有85元。

详解：4. 三棵树上共有48只鸟. 后来，第一棵树上有一半的鸟飞到了第二棵树上；之后，第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上；最后，第三棵树上又有10只鸟飞到了第一棵树上，此时三棵树上的鸟一样多. 问：一开始三棵树上各有几只鸟？答案：第一棵树上有12，第二棵23，第三棵135. 1997年张伯伯45岁，小方9岁，在哪一年张伯伯的年龄是小方年龄的4倍？答案：小方12岁那年。

高思学校-计算机竞赛课本-四年级-上册介绍本文档是关于高思学校计算机竞赛课本的四年级上册的介绍。

内容概述四年级上册的计算机竞赛课本旨在帮助学生初步了解计算机科学和编程的基本概念和技能。

课本内容涵盖以下几个方面：1. 计算机科学基础知识- 研究计算机的基本原理和功能。

- 了解计算机硬件和软件的基本组成部分。

- 探索计算机的发展历史和应用领域。

2. 编程入门- 研究使用简单的图形编程界面进行编程。

- 掌握基本的编程概念，如变量、条件语句和循环结构。

- 创造和解决简单的编程问题，培养逻辑思维和问题解决能力。

3. 算法与数据结构- 了解算法的基本概念和作用。

- 掌握常见的数据结构，如数组、链表和栈。

- 研究如何设计和实现简单的算法和数据结构。

4. 互联网和网络安全- 理解互联网的工作原理和基本组成。

- 研究如何使用互联网进行信息搜索和资源共享。

- 探索网络安全的重要性和常见的安全风险。

研究目标通过完成本课本的研究，学生将达到以下几个方面的研究目标：1. 掌握计算机科学的基本概念和技能。

2. 培养良好的逻辑思维和问题解决能力。

3. 培养对编程的兴趣和创造力。

4. 了解互联网和网络安全的基本知识。

5. 培养团队合作和沟通能力。

使用说明本课本为四年级学生设计，建议学生根据教师的指导，按照章节顺序逐步研究。

每个章节包含理论知识的介绍和相应的练题。

学生可以通过课堂上的互动讨论和实践编程来巩固所学内容。

结语通过本课本的学习，学生将初步了解计算机科学和编程的基本知识和技能。

希望学生们在学习过程中能够积极参与，发现计算机科学的乐趣，并用所学知识解决现实生活中的问题。

祝愿学生们在计算机竞赛中取得优异的成绩！。

第24讲逻辑推理一内容概述简单的逻辑推理问题，学会假设法和列表法。

典型例题兴趣篇1．甲、乙、丙3人中有1人是牧师，有1人是骗子，还有1人是赌棍，牧师从不说谎，骗子总说谎，赌棍有时说真话有时说谎话．甲说：“我是牧师．”乙说：“我是骗子．”丙说：“我是赌棍．”请问：甲、乙、丙3人中谁是牧师？谁是骗子？谁是赌棍？答案：甲是牧师，丙是骗子，乙是赌棍解析：在这三句话中，牧师只可能说“我是牧师”，所以牧师一定是甲．骗子不会说“我是骗子”，所以乙一定不是骗子．那么乙只能是赌棍，剩下丙就是骗子。

结论就是：甲是牧师，乙是赌棍，丙是骗子．2．有3只盒子，第1只盒子里装有2个黑球，第2只盒子里装有2个白球，第3只盒子里装有黑球和白球各1个，现在3只盒子上的标签全贴错了，你能否仅从其中1只盒子里拿出1个球来，就能确定这3只盒子里各装的是什么球？答案：从标有一黑一白的盒子里拿出一个球解析：从标有一黑一白的盒子里拿出一个球：①如果是白球，这个盒，子里装的既不是一黑一白，也不是两个黑球，只能是两个白球，接下来，标着两个黑球的盒子里装的既不是两个黑球，又不是两个白球，就只能是一黑一白．剩下标着两个白球的盒子里装的是两个黑球．②如果拿出的是黑球，标有一黑一白的盒子里装的就是两个黑球．而标有两个白球的盒子里装的是一黑一白．剩下标有两个黑球的盒子里装的是两个白球．以上说明这样拿是完全可以确定各盒情况的，3．墨爷爷手里握有2枚硬币，他让萱萱、小高和墨莫猜哪只手握有硬币．萱萱说：“左手没有，右手有．”小高说：“右手没有，左手有．”墨莫说：“不会2只手都没有，我猜左手没有．”结果3个人的话都说对一句，说错一句．请问：墨爷爷是怎么握住硬币的？答案：两只手里都有解析：由于墨莫的前一句肯定是对的，所以后一句是错的，墨爷爷的左手里有硬币．那么萱萱前一句就是错的，后一句是对的，则墨爷爷的右手里也有硬币．所以墨爷爷的两只手里都有硬币．小高的话正好一对一错，满足题目要求．4．甲、乙、丙、丁4位同学的运动衫上印上了不同的号码．赵说：“甲是2号，乙是3号．”钱说：“丙是4号，乙是2号，”孙说：“丁是2号，丙是3号，”李说：“丁是1号，乙是3号．”只知道赵、钱、孙、李每人都只说对了一半，请问：丙的号码是几号？答案：4号解析：如果赵的话前半句对后半句错，则甲是2号，乙不是3号．那么钱说乙是2号就是错的，它的前半句就是对的，即丙是4号．孙说丁是2号也是错的，所以丙是3号，这就和丙是4号矛盾了．如图1所示：所以甲不是2号，乙是3号，那么钱说乙是2号就是错的，丙是4号．孙说丙是3号是错的，丁是2号．李说丁是1号是错的，乙是3号．这样就没有矛盾，如图2所示：最后得到：甲是1号，乙是3号，丙是4号，丁是2号．5．A、B、C、D4人在争论今天是星期几.A说：“明天是星期五．”B说：“昨天是星期日，”C说：“你们俩说的都不对．”D说：“今天不是星期六．”实际上这4人中只有1人说对了．请问：今天是星期几？答案：星期六解析：仔细分析这4个人说的话，就可以发现，A、B、C三个人说的话中肯定有一个人说的是对的，即如果C说得不对，那么A和B就一定有一个是对的．所以，要么C说的是对的，要么A和B中一定有一个是对的．因为这三个人中一定有一个是对的，所以D就肯定是错的，那么今天就是星期六．6．5胞胎穿着颜色各异的衣服如图24-1站成一排，图中标出了他们穿的衣服的颜色．为了帮助我们分辨他们，5胞胎的妈妈告诉我们如下信息：①小蓝在小红的旁边；②小黑没有穿白色衣服；③穿绿色衣服的不是小绿；④小黑和小蓝中间隔了2个人；⑤小红在最边上．请问：小白今天穿了什么颜色的衣服？答案：绿色解析：列表格，由条件②③，可列出表一：由条件⑤知，小红穿红色或白色衣服；又由条件①知，小蓝穿蓝色或黑色衣服；又由条件④知，小黑穿红色衣服，小蓝穿黑色衣服，所以小红穿白色衣服！小绿穿蓝色衣服，小白穿绿色衣服，如表二所示：7．联欢晚会上，萱萱、墨莫和小高3人表演节目，他们都穿着上衣、裤子，戴着帽子，每种服饰的颜色都是红、白、绿色．已知：①每个人的服饰都恰好有红、白、绿3种颜色，并且没有2个人的所有服饰颜色都一样；②墨莫和小高穿着相同颜色的上衣；③有2个人穿的都是白裤子；④墨莫戴着白帼子；⑤萱萱穿着绿色的上衣．请问：小高穿着什么颜色的上衣？答案：红色解析：列表格，由条件④⑤，可列出表一：由条件①每个人的服饰都恰好有红、白、绿三种颜色和条荐沓有两个人穿的都是白裤子，则墨莫不能穿白裤子，所以萱萱和小高穿白裤子，进而得知萱萱的帽子是红色．由条件②知，墨莫和小高穿着相同颜色的上衣，只能是红色，如果是绿色，则小高和萱萱的所有服饰颜色都一样，与条件①矛盾，所以墨莫穿绿色裤子，小高戴绿色帽子，如表二所示：8．甲、乙、丙3位老师分别教四年级(3)班的语文、数学和英语．已知：甲老师不教英语；英语老师是二个学生的哥哥；丙是一位女老师，她比数学老师活泼．请问：乙老师教什么课？答案：英语解析：因甲不是英语老师，又英语老师是一个男的，那么丙也不是英语老师，所以只能乙是英语老师，而且丙不是数学老师，所以丙是语文老师，那么甲就是数学老师．9．甲、乙、丙、丁4名同学同在一间教室里，他们当中一个人在做数学题，一个人在念英语，一个人在看小说，一个人在写信．已知：①甲不在念英语，也不在看小说；②如果甲不在做数学题，那么丁不在念英语；③有人说乙在做数学题，或在念英语，但事实并非如此；④丙既不在看小说，也不在念英语．请问：在写信的是谁？答案：丙解析：由①③④得到表一（“√”表示在做这件事，“>：”表示没有做这件事）：由上表，得丁在念英语，又由于②，得知甲在做数学题，进而得到丙在写信，乙在看小说．于是得到表二：10.萱萱、小高、墨莫去参加一次奥运活动，他们3人分别戴着3种不同颜色的帽子，穿着3种不同颜色的衣服，已知：①帽子和衣服的颜色都只有红、黄、蓝3种；②萱萱没戴红帽子，小高没戴黄帽子；③戴红帽子的那个人没有穿蓝衣服；④戴黄帽子的那个人穿着红衣服；⑤小高没有穿黄色衣服，请问：萱萱、小高、墨莫各戴什么颜色的帽子，穿什么颜色的衣服？答案：萱萱戴黄帽子，穿红衣服；小高戴蓝帽子，穿蓝衣服：墨莫戴红帽子，穿黄衣服．解析：由条件②知小高没戴黄帽子，结合条件④得，他没穿红衣服，由条件⑤知他又没有穿黄衣服，所以小高穿的是蓝衣服，而条件③意思就是穿蓝衣服的人没有戴红帽子，则小高戴的不是红帽子，所以他戴的只能是蓝帽子．由条件②知萱萱没戴红帽子，所以墨莫戴红帽子，萱萤戴黄帽子．由条件④知道萱萱穿的是红衣服，则墨莫穿的就是黄衣服．如表所示：（“√”表示这个人戴这一种帽子或穿这一种衣服，“×”表示不戴这一种帽子或不穿这一砷衣服）拓展篇1．甲、乙、丙3人中有1人是牧师，有1人是骗子，还有1人是赌棍．牧师从不说谎，骗子总说谎，赌棍有时说真话有时说谎话，甲说：“丙是牧师．”乙说：“甲是赌棍，”丙说：“乙是骗子．”请问：甲、乙、丙3人中准是牧师？谁是骗子？谁是赌棍？答案：乙是牧师，丙为骗子，甲为赌棍．解析：方法一：①若甲说真话，那么丙为牧师，因为牧师说真话，则乙为骗子，所以甲不是赌棍，这不可能；②若乙说真话，那么甲为赌棍，医为乙说真话且不为赌棍，所以乙是牧师，进而可以判定丙为骗子且说假话，符合要求：③若丙说真话，那么乙是骗子，根据他的话知甲不是赌棍，但甲又不能是牧师，从而得出矛盾．乙是牧师，丙为骗子，甲为赌棍．方法二：①是牧师，根据他说的话推出丙也是牧师，这不可能，②若乙是牧师，那么乙说真话，从而甲是赌棍，丙只能是骗子，符合题意；③若丙是牧师，则乙是骗子，根据乙的话推出甲不是赌棍，但这是不可能的，所以乙是牧师，丙是骗子，甲是赌棍．2．期末考试结束后，甲、乙、丙、丁4名同学在一起议论，甲说：“自然成绩第一名是丁．”乙说：“数学成绩第一名是丙．”丙说：“语文成绩第一名不是甲，”丁说：“英语成绩第_名是乙，”成绩公布后发现，这四名同学确实分别取得了语文、数学、英语、自然的第一名，但只有取得语文和自然第一名的学生做出的猜测是正确的．请问：数学成绩第一名是谁？答案：甲解析：如图1，假设甲的话是正确的，那么由他的话知丁自然第一名，所以丁说了真话，从而乙是莫语第一名，同时因为“只有语文和自然第一名说真话”，所以甲是语文第-. 3个人的身份都确定后，丙只能是数学第一，但根据乙猜测错误知他不是数学第一，矛盾，假设不成立，所以甲的话是错误的．如图2，那他不可能是语文第一名，则丙的猜测正确，那么他是语文或者自然第一名，这样乙的猜测是；错误的，已知3个人是1对2错，那么丁的猜测必然是正确的，乙英语第一，由此便知猜测错误的甲是数学第一．3．甲、乙、丙、丁4人对A先生的藏书数目作了一个估计，甲说：“A先生有500本书．”乙说：“A先生至少有1000本书．”丙说：“A先生的书不到2000本，”丁说：“A先生最少有1本书，”实际上这4个人的估计中只有一句是对的，问：A先生究竟有多少本书？答案：没有书解析：方法一：①若甲是对的，A有500本书，从而丁肯定也是对的；②若乙是对的，同样也可以推出丁是对的；③若丁是对的，要是书的数目不少于1000本，乙是对的，要是书的数目不到1000本，丙是对的，都与“只有一个人的估计正确”不符；注意A丁的意思是A至少有一本书，既然他是错的，所以A先生，有书，即0本，这时只有丙的估计正确，符合题意．方法二：由于乙的话和丙的话从逻辑上考虑不能都错，于是他们中至少有一个人是对的，又因一个人的估计正确，所以丁一定是错的，因此知A先生没有书．4．法官在审理一起盗窃案的过程中，对4名犯罪嫌疑人甲、乙、丙、丁进行审问．甲说：“罪犯在乙、丙、丁3人之中．”乙说：“我没有作案，是丙偷的，”丙说：“甲、丁之中有1个是罪犯，”丁说：“乙说的是事实．”如果这4个人中有2人说的是真话，另外2人说了假话，而且只有1个罪犯，请你判断：罪犯是谁？答案：丁解析：方法一：①设甲为罪犯，于是甲说假话，丙的判断是正确的，乙的判断是错误的，而丁附和乙，也是错误的，4个人中只有丙说真话，不对；②若乙为罪犯，为1真3假（甲为真）；③若丙为罪犯，为3真1假（丙为假）；④若丁为罪犯，为2兵2假，符合题意．所以罪犯是丁．方法二：发现乙、丁观点相同，所以他们的话或同真或同假，又因为有2个人说真话，2个人说假话，所以甲和丙的话真伪性相同，但甲和丙不能都说假话，不然有2个人是罪犯，所以他们说真话，罪犯是丁．5．爱丽丝梦游仙境时，误人一片魔法森林——健忘森林．在森林中徘徊了很久以后，爱丽丝很想知道今天是星期几，这时她刚巧碰到了老由羊．爱丽丝赶忙问它：“请问您知道今天是星期几吗？”老山羊回答说：“真糟糕，我也不记得了！不过，你可以去问问狮子和独角兽．狮子在星期一、二、三是说谎的；独角兽在星期四、五、六是说谎的；其余的日子，它们都会说真话．”于是，爱丽丝就去找狮子和独角兽，并问它们今天是星期几．独角兽回答说：“昨天是我说谎的日子．”狮子也回答说：“昨天是我说谎的日子，”请你帮爱丽丝想一想，今天到底是星期几呢？答案：星期四解析：如果狮子昨天说谎，今天也说谎，它会说“昨天我不说谎”；如果它昨天不说谎，今天也不说谎，它也会说“昨天我不说谎”，但它却说：“昨天是我说谎的尽子”，所以昨天和今天狮子一定有一天说谎，另一天不说谎．同理，得独角兽也是一天说谎一天不说谎．对于狮子来说，今天只可能是星期二或星期四，而对于独角兽来说，今天只可能是星期四或星期日，所以今天只能是星期四．6．某参观团根据下列条件从A、B、C、D、E这5个地方中挑选参观地点，①若去A地，则必须去B地；②B、C两地中至多去一地；③D、E两地中至少去一地；④C、D两地都去或者都不去；⑤若去E地，一定要去A、D两地．请问：参观团所去的地点有哪些？答案：C和D解析：方法一：假设参观团去了A地，通过条件①可知也去了B地．由②．B、C至多去一地，所以没有去C．根据④知D也没有去，因为条件③说“D、E至少去一地”，所以一定去了E．但是这样的话由⑤知去了D，这与前面矛盾．既然参观团没有去A，则由⑤知一定没有去E此时根据③知一定去了D，那么再由④知C也去了，最后根据②，肯定没有去B，所以参观团最终去了C和D．方法二：根据③和⑤发现，两地至少去一地，则参观团一定去了D，所以也去了C地，那么由②知没有去B．又根据⑤和①知A、E都不能去，不然会推出去B地得到矛盾．所以参观团去了C和D.7．某校数学竞赛，A、B、C、D、E、F、G、H这8位同学获得前八名，老师让他们猜一下谁是第一名.A说：“F或者H是第一名．”B说：“我是第一名，”C 说：“G是第一名，”D说：“B不是第一名，”E说：“A说得不对．”F说：“我不是第一名，H也不是第一名，”G说：“C不是第一名，”H说：“我同意A的意见．”老师指出：8个人中有3人猜对了，请问：第一名是谁？答案：c解析：方法一：假设A说的是正确的，F或者H得了第一名，那么B、C、E、F的猜测均是错误的，D、G、H是正确的，4个人猜对，矛盾，所以A猜错了，从而H也猜错了，这时E、F是正确的．如果B是正确的，那他第一，从而A、C、D、H均猜错，也是4个人猜对，矛盾，因为B猜测错误，所以D的猜测是正确的．至此，已经知道D、E、F猜对，所以C、G均错，这时根据G的话知道C是第～名。

教师版第24讲逻辑推理一兴趣篇1．甲、乙、丙三人中有一人是牧师，有一人是骗子，还有一人是赌棍．牧师从不说谎，骗子总说谎，赌棍有时说真话有时说谎话．甲说：“我是牧师．”乙说：“我是骗子．”丙说：“我是赌棍．”请问：甲、乙、丙三人中谁是牧师?谁是骗子?谁是赌棍?答；甲是牧师，乙是赌棍，丙是骗子。

分析；因为牧师不说谎，所有甲是牧师，同理骗子总说谎所有丙是骗子，赌棍有时说真话有时说谎话所以乙是赌棍。

2．有三只盒子一只盒子里装有两个黑球，另一只盒子装有两个白球，还有一只盒子里装有黑球和白球各一个．现在三只盒子上的标签全贴错了．你能否仅从其中一只盒子里拿出一个球来，就确定这三只盒子里各装的是什么球?答；先那贴有一黑一白的盒子。

分析；因为三只盒子上的标签全贴错了，所以贴有一黑一白的盒子里一定是两黑或两白，如果从盒子里拿出黑的球，那么盒子里就是两个黑球，贴有两黑的就两白，贴有两白的就是一黑一白，如果从盒子里拿出白球同理如上。

3．费叔叔手里握有两个硬币，他让小悦、冬冬和阿奇猜哪只手握有硬币．小悦说：“左手没有，右手有．”冬冬说：“右手没有，左手有．”阿奇说：“不会两手都没有，我猜左手没有．”结果三个人的话都说对一句，说错一句．请问：费叔叔是怎么握住硬币的?答；两个手都有，分析：小悦说左手没有是对的，那么，冬冬说左手有就是错误的，那么，冬冬说右手没有也就是对了，这样两个手都没有，不符合题意，所以小悦说的右手有是对，冬冬说的左手有为对，阿奇说的不会两手都没有为对，所以费叔叔两个手都有。

4. 甲、乙、丙、丁四位同学的运动衫上印上了不同的号码：赵说：“甲是2号，乙是3号．”钱说：“丙是4号，乙是2号．”孙说：“丁是2号，丙是3号．”李说：“丁是1号，乙是3号．”又知道赵、钱、孙、李每人都只说对了一半．请问：丙的号码是几号?答：丙是4号。

分析；我们知道赵、钱、孙、李每人都只说对了一半．假如赵说甲是2号为对，那么钱说丙是四号就是对的，孙说的3号也为对啦，那么孙说的就和钱说的就互相矛盾啦，所以说的乙为3号为对，那么丙就是四号。

学习-----好资料第5讲竖式问题内容概述以字母或汉字表示数字的竖式问题，学会选择适当的突破口，并逐步解决问题；能够将文字叙述的题目转化为数字谜形式，便于直观地解决问题。

典型问题兴趣篇1.如图5-1所示，每个英文字母代表一个数字，不同的字母代表不同的数字，其中“G”代表“5”，“A”代表“9”，“D”代表“0”，“H”代表“6”.问：“I”代表的数字是多少？分析：也一定有A+E=HC=4，A+D=D，所以,它们的和一定有进位，所以，、2、F分别是1没有用，所以1、2、3、8B，现在还剩进位，所以E=7I=3.的加法竖式中，不同的汉字代表不同的数字，相同的汉字代）在图5-22. （1 表相同的数字，那么每个汉字各代表什么数字？的减法竖式中，不同的汉字代表不同的数字，相同的汉字代表相在图5-3(2)同的数字，那么每个汉字各代表什么数字？分析：，卒=1（1）观察可得：车，马=卒，所以兵=5=0，兵+兵马，所炮=，+1=5，所以马=4炮+=2以炮5240+5210=10450=2=马，所以：兵，=12）观察可得：炮，兵—兵=马，一定有借位，所以马=9，炮—兵（292=929—1221的竖式中，相同的汉字代表相同的3. 在图5-4+如果23+解数字，不同的汉字代表不同的数字，”所代表的三，那么“字++谜=30 数数字谜位数是多少？更多精品文档．学习-----好资料不同的汉字代表不同的数字，每个汉字代表一个数字，图5-5所示的竖式中，4. ”代表的四位数是多少？那么“北京奥运分析：奥++京，北+奥=0，所以可得要进位，所以；京=8 观察可得：北=1，北+京=9 ，运位，所以：奥=0+运=8，所以要进2=1809 北京奥运ABCDE所示的乘法竖式成立，那么5. 已知图5-6是多少？相同的符号代5-7的竖式中，6. (1) 在图表相同的数字，不同的符号代表不同的数字，那么☆、△、○分别代表什么数字？的竖式中，相同的符号代表5-8(2) 在图不同的符号代表不同的数字，相同的数字，那么☆、△、○分别代表什么数字？分析：三种可能，因为是三位数5、9,×△=△，所以△=1、）（1△，○=1，☆乘一位数等于四位数，所以1排除，经分析：△=5=2=2 ，○，当△=5时，☆=4、）△=15、6三种可能，排除12 （=3○=5时，△当=6☆，更多精品文档．学习-----好资料7. 如图5-9，相同的字母表示相同的数字，不同的字母表示不同的数字，那么十个方框中数字之和是多少？分析：B×B=B，所以B=1、5、6，三种可能，经分析1排除，A×B=B，所以B=5，A为奇数，三位数乘B得三位数，所以第一个方格中添1，一百多乘一位数得四位数，所以A只能是7、9，当A=7时，C=7，矛盾不成立；当A=9时，C=7，成立；所以：195×95=18525 1+9+1+7+5+1+8+5+2+5=448. 在图5-10和图5-11中的方格内填入适当的数字，使下列除法竖式成立.分析：，所以除数9=783（1）除数×=6003 ，所以被除数×6=522=87,8787=69÷6003=2465 5=145，所以被除数8=232，所以除数=29,29×（2）除数×29=85÷2465所示的除法竖式中填入合适的数字，使得竖式成立，那么其中的商5-129.在图是多少？分析：三= 除数×7=两位数，除数×另一个一位数，所以除数只能是位数，且三位数的十位上是2 ，9=12614,14×7=98,14×=79所以除数更多精品文档．好资料学习-----后所得乘积恰好是将原来的四位数各位数字顺序910. 有一个四位数，它乘以.颠倒而得的新四位数，求原来的四位数拓展篇不同的汉字代表不同的数字，相同的汉字代表相同的数字，和5-14中，1. 在图5-13. 求出它们使竖式成立的值分析：，四个语、语=5 （1）观察得：巧=1，所以三个英相加得数，进2相加得20，所，向前进2的个位是8，所以英得6 以学=4 以学+学得数个位也是8，所1465+林=7，奥++=6，奥林+匹进2，所以林2 （）观察的奥+林有进1，所以奥6789=83，所以匹，克=9 匹+克进，在这个算式中，相2. 如图5-15不同的同的字母代表相同的数字，、A字母代表不同的数字，那么数字分别是多少？B、C分析：有借位，没有借位，C—BCA=A，—B=B,所以C—AC观察—A=4A=A，所以B=9，所以有借位且，C=8，已知C—B—B=B8、4、9不同的字母表示不同的数在图5-16的竖式中，相同的字母表示相同的数字，3. 字，并且A<B<C<D. 问：竖式中的和是多少？分析：D=5 C=4，，，观察得A=2B=3 2233+3344+4455=10032更多精品文档．学习-----好资料4. 在图5-17的竖式中，相同的汉字表示相同的数字，不同的汉字表示不同的数字，那么“”所代表的七位数是多少？携手上海世博会分析：，个=9，手=0，上观察得，黄金三角：携=1，所=7位数的和肯定要进位，要使进1为，则博，=6位，办海=4，假设百位向前进2以会只能是2，，位，办=5，成立，1094382 ；假设百位向前进3=8当世=3时，在；，成立，1094872=8时，在=3当世小悦写了一个四位数，冬冬把这个四位数的个位抹掉，变成了一个三位数，5. 阿奇又把这个三位数的个位抹掉，变成了一个两位数，最后把这三个数加起来，小悦原来写的四位数是多少？结果刚好是7826.分析：利用位值原理ABCD+ABC+AB=78261000A+100B+10C+D+100A+10B+C+10A+B=1110A+111B+11C+D=7826D=1 56-55=1 则当则B=0 C=5时－时当A=778267770=56 7051即一个各位数字互不相同的三位数，用它的三个数字组成一个最大的三位数，6. 再用这三个数字组成一个最小的三位数，组成的这两个三位数之差正好是原来. 求原来的三位数的三位数.更多精品文档．学习-----好资料移到左边首位数字前面，所构成44，将这个7. (1) 一个自然数的个位数字是 4倍，那么原数最小是多少？的新数恰好是原数的一个五位数，将它的各位数字顺序颠倒就可以得到一个新的五位数，而且(2)/4倍，那么原来的五位数是多少这个新的五位数恰好是原数的）（1219782）（中的一个数字，不同的字母2，……908. 如图5-18，每一个英文字母代表，1 、RF分别代表什么数字？、、、代表不同的数字，则字母AQT更多精品文档．学习-----好资料分析：不QAQ×T=1符合题意，当Q=6时为5或6 当Q=5时A=2 .........QTAQ等于T=1 则........AQ×T=AQF=3R=7，Q=5，T=1，A=2，所以“美”三个汉字分别代表三个各不相同的“峡”、中的竖式里，“江”、9. 图5-19. 数字，请把这个竖式写出来分析：=6 ，所以美0,1,5,6中的一个，通过实验排除0,1,5先确定美是□□江，则=×江4或8之一，又因为江峡美或美通过确定江是2 排除，所以江=24或8=8=□□□峡，则峡由于江峡美×峡所示的除法5-2010. 请把如图竖式中空缺的数字补上，其中的商是多少？分析：1 7 则除数个位是7，商的十位数字是=6.........6□□×□□除数的十位数3=×□□□61 则商的个位数字是，7.........6□8 字是更多精品文档．学习-----好资料11. 请把图5-21中的除法竖式补充完整。

第17讲数列与数表内容概述通过观察数列或数表中的已知数据，发现规律并进行填补与计算的问题，注意数表形式的多样性，计算时常常考虑周期性，或进行合理估算.典型问题兴趣篇1．1，1，4，2，7，3，10，1，13，2，16，3，19，1，22，2，25，3，…，100．请观察上面数列的规律，问：(1)这个数列一共有多少项? (2)这个数列所有数的总和是多少?答案：67；1783解析：间隔是是等差数列。

2．观察数组(1，2，3)，(3，4，5)，(5，6，7)，(7，8，9)的规律，求：(1)第20组中三个数的和；(2)前20组中所有数的和．答案：120；1260解析：（39，40，42），运用等差数列求和公式。

3．一个数列的第一项是l，之后的每一项是这样得到的：如果前一项是一位数，接着的一项就等于前一项的两倍；如果前一项是两位数，接着的一项就等于前一项个位数字的两倍．请问：(1)第100项是多少?(2)前100项的和是多少?答案：8；975解析：按规律写：1,2,4,8,16,12,4,8,16,12……四个数为一个周期4. 如图17-1，方格表中的数是按照一定规律填人的．请观察方格表，并填出“?”处的数．答案：105解析：四周数的差是一个等差数列。

5．如图17-2，数阵中的数是按一定规律排列的，请问：(1)100在第几行、第几列?(2)第20行第3列的数是多少?答案：（1）第25行第6列；（2）79解析：两行为一个周期。

观察除以8的余数与在第几列之间的关系。

6．如图17-3，从4开始的自然数是按某种规律排列的，请问：(1)100在第几行，第几列?(2)第5行第20列的数是多少?答案：（1）第1第25列；（2）81解析：两列为一个周期。

7. 如图17-4所示，把偶数2、4、6、8，排成5列．各列从左到右依次为第1列、第2列、第3列、第4列和第5列，请问：(1)100在第几行，第几列?(2)第20行第2列的数是多少?答案：（1）第15行第2列；（2）138解析：八个数为一个周期，可以把每个数先除以2转化成简单数列。

逻辑推理四年级奥数专题逻辑推理之列表法、假设法(★★★)甲、乙、丙、丁四个人中有教师、医生、律师、警察各一名，已知：⑴教师不知道甲的职业；⑶律师是丙的法律顾问；⑸乙和丙从未见过面。

(★★★) ⑵医生曾给乙治过病；⑷丁不是律师；根据以上条件判断甲的职业是________，乙的职业是________。

甲、乙、丙在2019年高考中，分别考取了北大，清华和理工大学的数学系，物理系和化学系，现知道下列情况⑴甲不在北大；⑶在北大的不学数学；⑸乙不学化学。

⑵乙不在清华；⑷在清华的学物理；根据以上情况判断甲、乙、丙三人各在哪个学校？哪个系？(★★★★) 有这样三个的职业人，他们分别姓李、蒋和刘，他们每人身兼两职，三个人的六种职业是作家、音乐家、美术家、话剧演员、诗人和工人，同时还知道以下的事实：⑴音乐家以前对工人谈论过对“古典音乐”的欣赏；⑵音乐家出国访问时，美术家和李曾去送行；⑶工人的爱人是作家的妹妹；⑷作家和诗人曾经在一起探讨“百花齐放”的问题；⑸美术家曾与姓蒋的看过电影；⑹姓刘的善下棋，姓蒋的和那作家跟他对奕时，屡战屡败。

请问他们的职业是什么？1(★★) 一个外地人路过一个小镇，此时天色已晚，于是他便去投宿。

当他来到一个十字路口时，他知道肯定有一条路是通向宾馆的，可是路口却没有任何标记，只有三个小木牌。

第一个木牌上写着：“这条路上有宾馆”。

第二个木牌上写着：“这条路上没有宾馆”。

第三个木牌上写着：“那两个木牌有一个写的是事实，另一个是假的。

相信我，我的话不会有错”。

假设你是这个投宿的人，按照第三个木牌的话为依据，你觉得你会找到宾馆吗？如果可以，哪条路上有宾馆？(★★★) 在老北京的一个胡同的大杂院里，住着4户人家，巧合的是每家都有一对双胞胎女孩。

这四对双胞胎中，姐姐分别是甲、乙、丙、丁，妹妹分别是a 、b 、c 、d 。

一天，一对外国游人夫妇来到这个大杂院里，看到她们8个，忍不住问：“你们谁和谁是一家的啊？” 乙说：“丙的妹妹是d 。