统计学第四版一元线性回归
- 格式:ppt
- 大小:1.25 MB
- 文档页数:78

回归分析与时间序列一、一元线性回归11。
1 (1)编辑数据集,命名为linehuigui1.dat输入命令scatter cost product,xlabel(#10,grid) ylabel(#10,grid),得到如下散点图,可以看到,产量和生产费用是正线性相关的关系。
(2)输入命令regcost product,得到如下图:可得线性函数(product为自变量,cost为因变量):y=0。
4206832x+124。
15,即β0=124。
15,β1=0。
4206832(3)对相关系数的显著性进行检验,可输入命令pwcorr cost product,sig star (.05) print(。
05),得到下图:可见,在α=0。
05的显著性水平下,P=0。
0000<α=0。
05,故拒绝原假设,即产量和生产费用之间存在显著的正相关性。
11。
2 (1)编辑数据集,命名为linehuigui2。
dat输入命令scatterfenshu time,xlabel(#4, grid) ylabel(#4,grid),得到如下散点图,可以看到,分数和复习时间是正线性相关的关系。
2)输入命令cor fenshu time计算相关系数,得下图:可见,r=0.8621,可见分数和复习时间之间存在高度的正相关性。
11.3 (1)(2)对于线性回归方程y=10-0。
5x,其中β0=10,表示回归直线的截距为10;β1=—0.5,表示x变化一单位引起y的变化为—0.5。
(3)x=6时,E(y)=10-0.5*6=7.11.4(1)R2=SSRSST =SSRSSR+SSE=3636+4=0.9,判定系数R2测度了回归直线对观测数据的拟合程度,即在分数的变差中,有90%可以由分数与复习时间之间的线性关系解释,或者说,在分数取值的变动中,有90%由复习时间决定。
可见,两者之间有很强的线性关系.(2)估计标准误差S e=√SSEn−2=√418−2=0.25分,即根据复习时间来估计分数时,平均的估计误差为0.25分.11.5 (1)编辑数据集,命名为linehuigui3。

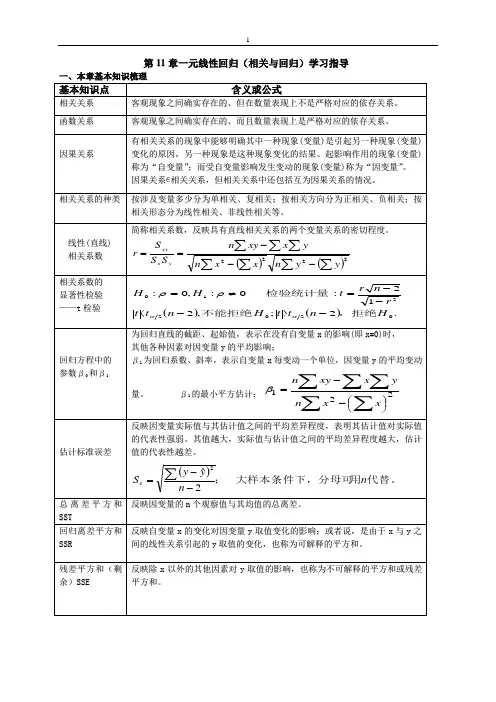
第11章一元线性回归(相关与回归)学习指导一、本章基本知识梳理基本知识点含义或公式相关关系 客观现象之间确实存在的、但在数量表现上不是严格对应的依存关系。
函数关系 客观现象之间确实存在的、而且数量表现上是严格对应的依存关系。
因果关系有相关关系的现象中能够明确其中一种现象(变量)是引起另一种现象(变量)变化的原因,另一种现象是这种现象变化的结果。
起影响作用的现象(变量)称为“自变量”;而受自变量影响发生变动的现象(变量)称为“因变量”。
因果关系∊相关关系,但相关关系中还包括互为因果关系的情况。
相关关系的种类 按涉及变量多少分为单相关、复相关;按相关方向分为正相关、负相关;按相关形态分为线性相关、非线性相关等。
线性(直线) 相关系数 简称相关系数,反映具有直线相关关系的两个变量关系的密切程度。
()()∑∑∑∑∑∑∑---==2222y yn x xn yx xy n SS S r yx xy相关系数的 显著性检验 ——t 检验 ()().2;,212:0:,0:020221Hn t t Hn t t rn r t HH,拒绝不能拒绝检验统计量-〉-〈--=≠=ααρρ回归方程中的 参数β0和β1为回归直线的截距、起始值,表示在没有自变量x 的影响(即x =0)时,其他各种因素对因变量y 的平均影响;β1为回归系数、斜率,表示自变量x 每变动一个单位,因变量y 的平均变动量。
β1的最小平方估计:∑∑∑∑∑⎪⎭⎫ ⎝⎛--=221x x n yx xy nβ估计标准误差反映因变量实际值与其估计值之间的平均差异程度,表明其估计值对实际值的代表性强弱。
其值越大,实际值与估计值之间的平均差异程度越大,估计值的代表性越差。
()代替。
用大样本条件下,分母可;n n yyS e 2ˆ2--=∑总离差平方和S S T反映因变量的n 个观察值与其均值的总离差。
回归离差平方和S S R 反映自变量x 的变化对因变量y 取值变化的影响;或者说,是由于x 与y 之间的线性关系引起的y 取值的变化,也称为可解释的平方和。



一元线性回归分析摘要:一元线性回归分析是一种常用的预测和建模技术,广泛应用于各个领域,如经济学、统计学、金融学等。
本文将详细介绍一元线性回归分析的基本概念、模型建立、参数估计和模型检验等方面内容,并通过一个具体的案例来说明如何应用一元线性回归分析进行数据分析和预测。
1. 引言1.1 背景一元线性回归分析是通过建立一个线性模型,来描述自变量和因变量之间的关系。
通过分析模型的拟合程度和参数估计值,我们可以了解自变量对因变量的影响,并进行预测和决策。
1.2 目的本文的目的是介绍一元线性回归分析的基本原理、建模过程和应用方法,帮助读者了解和应用这一常用的数据分析技术。
2. 一元线性回归模型2.1 模型表达式一元线性回归模型的基本形式为:Y = β0 + β1X + ε其中,Y是因变量,X是自变量,β0和β1是回归系数,ε是误差项。
2.2 模型假设一元线性回归模型的基本假设包括:- 线性关系假设:自变量X与因变量Y之间存在线性关系。
- 独立性假设:每个观测值之间相互独立。
- 正态性假设:误差项ε服从正态分布。
- 同方差性假设:每个自变量取值下的误差项具有相同的方差。
3. 一元线性回归分析步骤3.1 数据收集和整理在进行一元线性回归分析之前,需要收集相关的自变量和因变量数据,并对数据进行整理和清洗,以保证数据的准确性和可用性。
3.2 模型建立通过将数据代入一元线性回归模型的表达式,可以得到回归方程的具体形式。
根据实际需求和数据特点,选择适当的变量和函数形式,建立最优的回归模型。
3.3 参数估计利用最小二乘法或最大似然法等统计方法,估计回归模型中的参数。
通过最小化观测值与回归模型预测值之间的差异,找到最优的参数估计值。
3.4 模型检验通过对回归模型的拟合程度进行检验,评估模型的准确性和可靠性。
常用的检验方法包括:残差分析、显著性检验、回归系数的显著性检验等。
4. 一元线性回归分析实例为了更好地理解一元线性回归分析的应用,我们以房价和房屋面积之间的关系为例进行分析。




第十一章一元线性回归练习题答案二.填空题 1. 不能;因为该相关系数为样本计算出的相关系数,它的大小受样本数据波动的影响,它是否显著尚需检验;t 检验;2.图1;不能;因为图1反映的是线性相关关系,图2反映的是非线性性相关关系,相关系数只能反映线性相关变量间的相关性的强弱,不能反映非线性相关性的强弱。
三.计算题1.(1) SSR 的自由度是1,SSE 的自由度是18。
(2)2418/6080220/1/==-=SSE SSR F(3)判定系数%14.57140802===SST SSR R 在y 的总变差中,由57.14%的变差是由于x 的变动说引起的。
(4)7559.05714.02-=-=-=R r相关系数为-0.7559。
(5)线性关系显著和:线性关系不显著和y x y x H 10H :因为414.424=>=αF F,所以拒绝原假设,x 与y 之间的线性关系显著。
2.(1)方差分析表df SS MS F Significance F回归分析 1 425 425 85 0.017 残差 15 75 5 - - 总计16500---(2)判定系数%8585.05004252====SST SSR R表明在维护费用的变差中,有85%的变差可由使用年限来解释。
(3)9220.085.02===R r二者相关系数为0.9220,属于高度相关(4)x y248.1388.6ˆ+= 分布;显著。
的自由度为t n r n r t 2);12||2---=回归系数为1.248,表示每增加一个单位的产量,该行业的生产费用将平均增长1.248个单位。
(5)线性关系显著性检验:线性关系显著:生产费用和产量之间性关系不显著生产费用和产量之间线10:H H因为Significance F=0.017<05.0=α,所以线性关系显著。
(6)348.3120248.1388.6248.1388.6ˆ==⨯++=x y当产量为10时,生产费用为31.348万元。

一元线性回归教案引言一元线性回归是统计学中非常重要的一种回归分析方法。
它能够通过建立一个线性模型,根据自变量的值来预测因变量的值。
本教案将介绍一元线性回归的基本概念、原理和应用场景,并通过示例演示如何进行一元线性回归分析。
目录1.什么是一元线性回归?2.一元线性回归的原理3.数据的处理与准备4.拟合一元线性回归模型5.模型评估与预测6.应用案例分析7.总结1. 什么是一元线性回归?一元线性回归是指只有一个自变量和一个因变量的线性回归模型。
它的数学表达式为:Y = β0 + β1X + ε,其中Y是因变量,X是自变量,β0和β1是模型的参数,ε是误差项。
一元线性回归的目标是找到最合适的β0和β1,使得模型对观测数据点的拟合程度最优。
2. 一元线性回归的原理一元线性回归的原理基于最小二乘法,即通过最小化观测值与模型预测值之间的差异来确定模型的参数。
最小二乘法可以通过求解正规方程来获得最优的参数估计值。
3. 数据的处理与准备在进行一元线性回归分析之前,需要对数据进行处理和准备。
这包括数据清洗、变量选择和数据可视化等步骤。
本节将介绍常用的数据处理方法,以及如何选择适当的自变量和因变量。
4. 拟合一元线性回归模型拟合一元线性回归模型是通过最小二乘法来确定模型的参数估计值。
本节将介绍如何使用Python中的scikit-learn库来拟合一元线性回归模型,并分析模型的拟合结果。
5. 模型评估与预测在拟合一元线性回归模型之后,需要对模型进行评估和预测。
本节将介绍常用的评估指标,如均方误差(MSE)和决定系数(R-squared),以及如何使用模型进行预测。
6. 应用案例分析本节将通过一个实际的数据集来展示一元线性回归的应用场景。
通过分析数据集中的自变量和因变量之间的关系,我们可以建立一元线性回归模型,并对模型进行评估和预测。
7. 总结本教案从一元线性回归的基本概念和原理开始,通过示例和实践对一元线性回归进行了详细讲解。
从统计学看线性回归(1)——⼀元线性回归⽬录1. ⼀元线性回归模型的数学形式2. 回归参数β0 , β1的估计3. 最⼩⼆乘估计的性质 线性性 ⽆偏性 最⼩⽅差性⼀、⼀元线性回归模型的数学形式 ⼀元线性回归是描述两个变量之间相关关系的最简单的回归模型。
⾃变量与因变量间的线性关系的数学结构通常⽤式(1)的形式:y = β0 + β1x + ε (1)其中两个变量y与x之间的关系⽤两部分描述。
⼀部分是由于x的变化引起y线性变化的部分,即β0+ β1x,另⼀部分是由其他⼀切随机因素引起的,记为ε。
该式确切的表达了变量x与y之间密切关系,但密切的程度⼜没有到x唯⼀确定y的这种特殊关系。
式(1)称为变量y对x的⼀元线性回归理论模型。
⼀般称y为被解释变量(因变量),x为解释变量(⾃变量),β0和β1是未知参数,成β0为回归常数,β1为回归系数。
ε表⽰其他随机因素的影响。
⼀般假定ε是不可观测的随机误差,它是⼀个随机变量,通常假定ε满⾜:(2)对式(1)两边求期望,得E(y) = β0 + β1x, (3)称式(3)为回归⽅程。
E(ε) = 0 可以理解为ε对 y 的总体影响期望为 0,也就是说在给定 x 下,由x确定的线性部分β0 + β1x 已经确定,现在只有ε对 y 产⽣影响,在 x = x0,ε = 0即除x以外其他⼀切因素对 y 的影响为0时,设 y = y0,经过多次采样,y 的值在 y0 上下波动(因为采样中ε不恒等于0),若 E(ε) = 0 则说明综合多次采样的结果,ε对 y 的综合影响为0,则可以很好的分析 x 对 y 的影响(因为其他⼀切因素的综合影响为0,但要保证样本量不能太少);若 E(ε) = c ≠ 0,即ε对 y 的综合影响是⼀个不为0的常数,则E(y) = β0 + β1x + E(ε),那么 E(ε) 这个常数可以直接被β0 捕获,从⽽变为公式(3);若 E(ε) = 变量,则说明ε在不同的 x 下对 y 的影响不同,那么说明存在其他变量也对 y 有显著作⽤。
一元线性回归公式一元线性回归公式是一种基本的统计学模型,它在统计学和机器学习领域中都有广泛应用,可以用来预测和分析两个变量之间的关系。
一元线性回归的公式可以通俗地表达为:Y = +X,其中Y为因变量,X为自变量,α为截距项,β为斜率。
一元线性回归的本质就是对两个变量之间的线性关系进行拟合,同时计算出两个变量之间的斜率β和截距项α。
两个变量之间的线性关系能够概括为Y = +X,其中X是自变量,Y是因变量,α是压力,β是应力。
由于一元线性回归模型只分析两个变量之间的关系,因此该模型也称为双变量回归模型。
一元线性回归的原理是什么呢?一元线性回归的原理是使用最小二乘法(Least Squares)来找到最佳拟合参数,以使所有样本点和拟合曲线之间的总误差最小。
通过最小二乘法,系统可以根据输入数据自动计算出α和β参数,从而实现回归拟合。
一元线性回归公式是一种重要的统计模型,用于分析两个变量之间的关系。
它能够解决各种数量和定性难题,比如预测消费者行为、分析市场趋势等,以及帮助企业做出数据驱动的决策。
统计学家除了使用一元线性回归公式外,还可以使用多元线性回归来分析多个变量之间的关系,多元线性回归旨在更加准确地预测多元变量之间的关系,从而获得更准确的预测结果。
一元线性回归模型可以很容易地使用统计分析软件或者编程语言实现,它是实现数据驱动的管理层面的有力武器。
此外,一元线性回归模型在机器学习领域中也有着重要的作用,因为它可以用来训练算法,从而帮助计算机更准确地预测结果。
总的来说,一元线性回归公式是一种广泛应用的基础统计学模型,它可以帮助企业进行数据驱动的决策,也可以用于机器学习算法的训练,从而提高算法预测的准确性。