画立体图形(三视图)(上课用)
- 格式:ppt
- 大小:8.44 MB
- 文档页数:19

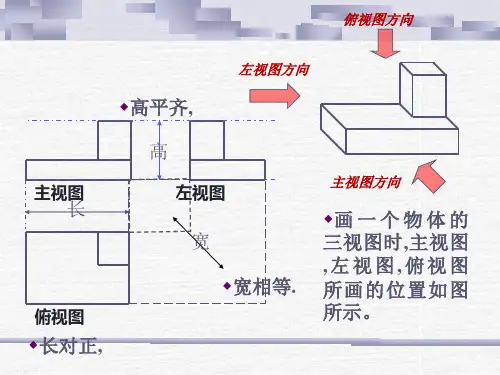





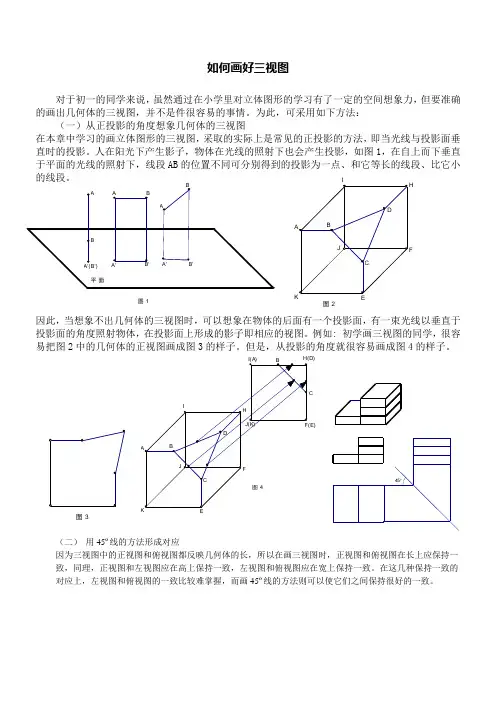
图 1
图
3
图 2
C
45 如何画好三视图
对于初一的同学来说,虽然通过在小学里对立体图形的学习有了一定的空间想象力,但要准确的画出几何体的三视图,并不是件很容易的事情。
为此,可采用如下方法:
(一)从正投影的角度想象几何体的三视图
在本章中学习的画立体图形的三视图,采取的实际上是常见的正投影的方法,即当光线与投影面垂直时的投影。
人在阳光下产生影子,物体在光线的照射下也会产生投影,如图1,在自上而下垂直于平面的光线的照射下,线段AB的位置不同可分别得到的投影为一点、和它等长的线段、比它小的线段。
因此,当想象不出几何体的三视图时,可以想象在物体的后面有一个投影面,有一束光线以垂直于投影面的角度照射物体,在投影面上形成的影子即相应的视图。
例如: 初学画三视图的同学,很容易把图2中的几何体的正视图画成图3的样子。
但是,从投影的角度就很容易画成图4的样子。
(二)用45º线的方法形成对应
因为三视图中的正视图和俯视图都反映几何体的长,所以在画三视图时,正视图和俯视图在长上应保持一致,同理,正视图和左视图应在高上保持一致,左视图和俯视图应在宽上保持一致。
在这几种保持一致的对应上,左视图和俯视图的一致比较难掌握,而画45º线的方法则可以使它们之间保持很好的一致。


七年级苏教版数学复习要点考点专题四:立体图形及三视图知识点一常见立体图形1.立体图形与平面图形①有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一平面内,它们是立体图形.②有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一平面内,它们是平面图形.3.常见立体图形的分类曲面体圆柱、圆锥、球体按是否有顶点是棱柱、棱锥、圆锥否圆柱、球体总结:在对几何体分类时首先确定分类的标准,分类标准不同,结果也就不同,不论选择哪种分类标准,都要做到不重、不漏.4、点、线、面、体体:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥都是几何体,几何体也称体.面:包围着体的是面.面有平面和曲面两种.线:面和面相交的地方形成线.点:线和线相交的地方是点.用运动的观点来看:点动成线、线动成面、面动成体.例1(中山区期末)三角形ABC绕BC旋转一周得到的几何体为()A.B.C.D.【解答】解:由图形的旋转性质,可知ABC旋转后的图形为C,故选:C.例2(邳州市期末)如图,在下列图形中,绕铅垂线旋转一周可得到如图所示几何体的是()A.B.C.D.【解答】解:A、是直角梯形绕高旋转形成的圆台,故A正确;B、是直角梯形绕底边的腰旋转形成的圆柱加圆锥,故B错误;C、绕直径旋转形成球,故C错误;D、绕直角边旋转形成圆锥,故D错误.故选:A.例3(皇姑区期末)下面是一个正方体,用一个平面去截这个正方体截面形状不可能为下图中的()A.B.C.D.【解答】解:无论如何去截,截面也不可能有弧度,因此截面不可能是圆.故选:D.知识点二几何体的表面展开图1.展开图:有些几何体的表面可以展开成平面图形,这个平面图形称为相应几何体的表面展开图.2.常见立体图形的平面展开图(1)圆柱的表面展开图是两个相同的圆面和一个长方形组成的;(2)圆锥的表面展开图是由一个圆面和一个扇形组成的;(3)棱柱的表面展开图是由两个相同的多边形和一个长方形组成的,侧面展开图是一个长方形。

第四章第2课立体图形的三视图(1)-七年级上册初一数学(人教版)一、引言本课主要介绍了立体图形的三视图。
在现实生活中,我们经常会遇到各种立体图形,比如立方体、长方体、圆柱体等等,而了解这些图形的三视图对我们理解和构造立体图形有重要的帮助。
本文将详细介绍立体图形的三视图的概念及其应用,帮助学生更好地理解和掌握立体图形的表达方式。
二、立体图形的三视图概念1. 什么是立体图形的三视图立体图形的三视图指的是一个立体图形在三个不同方向上的投影。
通常,我们可以将一个立体图形的三视图分别绘制在前视图、顶视图和侧视图上,以便更好地展示出其外观和尺寸。
2. 前视图、顶视图和侧视图的定义•前视图:立体图形在正对着它的方向上的投影视图,从正方向观察,是立体图形的正面视图。
•顶视图:立体图形在上方向的投影视图,从上方向观察,是立体图形的俯视图。
•侧视图:立体图形在侧面方向的投影视图,从一侧方向观察。
在绘制三视图时,我们一般按照一定的规则来绘制,以保证准确性和一致性。
三、绘制立体图形的三视图步骤绘制立体图形的三视图一般可以按照以下步骤进行:1. 确定各个视图的位置在绘制三视图之前,首先需要确定每个视图在纸上的位置。
一般来说,我们可以将前视图绘制在最上方,顶视图绘制在左侧,侧视图绘制在右侧,以保证三视图之间的关系清晰可见。
2. 绘制前视图在绘制前视图时,我们需要根据实际立体图形的形状和尺寸,在纸上垂直绘制图形的每个面。
可以用实线表示实际可见的支撑面,用虚线表示实际不可见的支撑面。
3. 绘制顶视图在绘制顶视图时,我们需要将立体图形向下投影至纸面上。
同样,可以用实线表示可见的支撑面,用虚线表示不可见的支撑面。
需要注意的是,顶视图在水平方向上的尺寸要与前视图保持一致。
4. 绘制侧视图在绘制侧视图时,我们将立体图形向左或向右投影至纸面上。
同样,用实线表示可见的支撑面,用虚线表示不可见的支撑面。
需要注意的是,侧视图在水平方向上的尺寸要与前视图和顶视图保持一致。
机械制图课程–三视图的画法引言在机械制图课程中,学习三视图的画法是非常重要的一部分。
通过正确绘制三视图,我们可以描述一个物体的外观和尺寸,为制造和加工提供准确的依据。
本文将介绍三视图的基本概念和画法,并提供一些实用的技巧和注意事项。
什么是三视图三视图是指一个物体的正视图、俯视图和侧视图,通过这三个视图可以全面而准确地描述物体的外观和尺寸。
•正视图:从物体的正面观察,以垂直于物体的视角绘制。
•俯视图:从物体的上方观察,以垂直于物体的视角绘制。
•侧视图:从物体的侧面观察,以垂直于物体的视角绘制。
通过绘制这三个视图,我们可以得到物体在不同方向上的形状和尺寸信息,利于设计和制造过程中的准确沟通和理解。
三视图的画法步骤绘制三视图的过程可以分为以下步骤:1.确定物体的投影方向:根据题目或实际需求,确定物体相对于观察者的位置和方向。
一般来说,正视图位于左侧,侧视图位于右侧,俯视图位于上方。
2.绘制物体的正视图:根据题目或实际需求,确定物体正视图的尺寸和比例,并按照比例在纸上绘制物体的形状和细节。
注意保持物体的轴线与视图之间的一致性。
3.绘制物体的俯视图:根据题目或实际需求,确定物体俯视图的尺寸和比例,并按照比例在纸上绘制物体的形状和细节。
注意保持物体的轴线与视图之间的一致性。
4.绘制物体的侧视图:根据题目或实际需求,确定物体侧视图的尺寸和比例,并按照比例在纸上绘制物体的形状和细节。
注意保持物体的轴线与视图之间的一致性。
通常侧视图位于俯视图的右侧。
5.标注尺寸信息:根据物体的实际尺寸确定比例尺,将尺寸信息标注在三视图上,包括长度、宽度、高度以及其他关键尺寸。
标注要清晰、准确,方便理解和后续的加工和制造。
6.完善细节部分:检查三视图的绘制是否完整和准确。
根据实际尺寸和细节,确定是否需要进一步添加细节信息,如孔的位置和直径、倒角的大小等。
三视图的绘制技巧和注意事项在绘制三视图时,应注意以下技巧和事项:•视图之间的一致性:保持三个视图之间的相对位置和比例一致,特别是轴线的位置和方向。
三视图画法了解物体的三视图,能正确地画出简单几何体的三视图是新课程的新内容之一.如何正确地画出简单几何体的主视图、左视图和俯视图呢?注意以下几点: 一、注意物体摆放的位置物体的三视图与物体摆放的位置有着十分密切的关系,同一个物体,摆放的位置不同,所得的三视图一般也不同.如图1的圆柱,它的主视图和左视图都是矩形,俯视图是圆,而如果把它摆放成如图2,则它的左视图就变成了圆,俯视图变成了矩形. 二、明确三种视图的形状画简单几何体三视图时,首先要明确各种视图的形状,熟记一些常见几何体三视图的形状,例如在正常的放置下,球的三视图都是圆;圆柱的主视图和左视图都是矩形,俯视图是圆;正方体的三视图都是正方形;圆锥的主视图和左视图都是三角形,俯视图是圆及圆心等. 三、准确三种视图的大小明确三种视图的形状后,在绘画时要注意各种视图的大小.视图的大小与几何体的大小有关,在不放大也不缩小的情况下,各种视图的大小应与几何体相应的大小相同.如果我们把几何体的大小分为长、宽和高,那么三视图中的主视图是由长和高组成的,其长和高分别与几何体的长和高相等;左视图是由高和宽组成的,其大小与几何体相应的大小一样;俯视图是由宽和长组成的,它的大小分别与几何体的宽和长相等.这些关系可概括为十五个字“主俯长对正,俯左宽相等,左主高平齐”.意思是说,主视图和俯视图的长与几何体的长相等,俯视图和左视图的宽与几何体的宽相等,左视图和主视图的高与几何体的高相等.大家可参见图3.四、注意实线与虚线的用法含有棱的几何体,它的棱在三视图中也要画出来.如果是看得见的棱,用实线画出,看不见的用虚线.如图4是一个正六棱柱,它的左视图是正六边形,其边长与底面的正六边形边长相等;主视图是一个长方形,长方形的长与六棱柱的长一样,高与六棱柱上下平行两面的距离相等,在主视图中我们还可以看到前面正中间一条棱和后面正中间一条棱,本来这两条棱都要画出,前者用实线,后者用虚线,但由于后面的棱与前面的棱在主视图中是重合的,故只须画出前面的这一条;俯视图也是长方形,长与主视图的长一样,宽是正六边形最长的对角线长,所看见的棱有两条,另两条看不见的棱在俯视图中与看得见的重合.因此,画出来的三视图如图5所示.例1 如图1,试画出该物体的三种视图. 错解:物体的三种视图如图2所示.分析:错解在左视图没有画出物体能看得到的轮廓线,俯视图的轮廓线画成了虚线.图1图2图4左视图正视图 俯视图图5正解:如图3所示.例2如图4,画出该几何体的三种视图.错解:几何体的三种视图如图5所示.分析:错解在左视图与主视图不等高,主视图与俯视图长不等,左、俯视图宽不相等.正解:如图6所示.例3画出如图7所示物体的三种视图.错解:如图8所示.分析:错解在俯视图看不见部分的轮廓画成实线.且俯视图没有画在主视图的下方.正解:如图9所示.。