当前位置：文档之家 › 十四种不拉维格子

十四种不拉维格子

  • 格式：doc
  • 大小：40.50 KB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

第六章 晶体内部结

第六章 晶体内部结


滑移面按其滑移的方向和距离可分为a、b、c、
n、d五种。
其中a、b、c为轴向滑移，移距分别为1/2a，
1/2b，1/2c。
n为对角线滑移，移距为1/2（a+b）or
1/2（b+c）等。
d为金刚石型滑移，移距为 1/4（a+b）等。
举例：金刚石晶体结构（示范晶体格架）
三、空间群
空间群为晶体内部结构的对称要素（操作）的组合。空间群 共有230种，空间群亦称之为费德洛夫群（Fedrov group）或 圣 佛利斯群（Schoenflies group） 。 空间群是从对称型（点群）中推导出来的，每一对称型（点 群）可产生多个空间群，所以32个对称型（点群）可产生230种 空间群。 空间群与对称型（点群）的区别： 对称型（点群） 有限图形(晶体形态) 点操作(有一个点不动) m，n，ni ， 空间群 无限图形（晶体结构） 空间操作（平移对称变换） m，n， ni ，ns，a，b，c， n，d
空间群与对称型（点群）体现了晶体内部结构的对称与晶
体外形对称的统一。如在晶体外形的某一方向上有4，则在 晶体内部结构中相应的方向可能是4、41、42或许43，也可
能有21。 空间群的国际符号包括两个组成部分，前一部分为大写英 文字母，表示格子类型(P、C、I、F)；后一部分与对称型 （点群）的国际符号基本相同，只是其中晶体的某些宏观对 称要素的符号需换成相应的内部结构对称要素的符号。 例如：P42/mnm，它的点群是什么？格子类型是什么？
2）底心格子(C):结点分布于平行六面体的角顶及上下一
对面的中心。
3）体心格子(Ⅰ):结点分布于平行六面体的角顶和体中心。
4）面心格子(F):结点分布于平行六面体的角顶和三对 面的中心。
晶体构造的几何理论

晶体构造的几何理论

▪单位晶胞可用晶胞参数来表征，其数值等
同于对应的单位平行六面体参数。
▪一般未加说明的晶胞一词是指单位晶胞。
例如：NaCl晶体的晶胞，对应的是立方面心格子， a=b=c=0.5628nm，α=β=γ=90°。许许多多该晶 胞在三维空间无间隙的排列就构成了NaCl晶体。（一 个晶胞含有4个NaCl分子）
例如，下图为具有L44P的平面格子。显然，4、5、6 与对称不符，3的轮廓虽然符合对称性，但结合其内 部结点的分布一起来考虑时，就与对称不符了。在1 和2中，则以1的面积最小，故应选1作为基本单位。
平行六面体的三根棱长a、b、c及其夹角α、 β、γ是表示它本身的形状、大小的一组参数， 称为单位平行六面体参数或格子常数。
四方体心格子
三
方
与本晶系
晶 系
对称不符
三方菱面体格子(标记为R)
三 、 六 方 晶 系
六方和三方原始格子
不符合六 方对称
等 轴
与本晶系
晶 系
对称不符
立方原始格子
I＝R 与空间格子 条件不符
立方体心格子
F＝I
F胞的概念
▪晶胞：是指晶体结构中的平行六面体单位，
代表格子类型（P、C、I、F）。后一部分与对称型国际符
号基本相同，只是将宏观对称要素符号换成相应的内部结 构对称要素的符号。
Cl－ Na＋
Cl- Na+
三、晶体内部构造的对称要素
❖晶体内部构造的对称属于微观的无限图形的对称， 不同于晶体外形的对称，外形的对称取决于内部构造 的对称，而且是宏观的有限图形的对称。
晶体的微观对称的主要特点如下： ⑴在晶体构造中，平行任何一个对称要素都有无穷多 的和它相同的对称要素。
⑵在晶体构造中出现了一种在晶体外形上不可能有的 对称操作——平移操作。
第一章结晶学基础-1.3.1十四种布拉维点阵_6.14ZSQ

第一章结晶学基础-1.3.1十四种布拉维点阵_6.14ZSQ

材料科学基础第1 章1.3.1 十四种布拉维点阵十四种布拉维点阵一、单位平行六面体的选取二、十四种布拉维点阵三、晶胞空间点阵的划分 空间点阵是一个由无限多结点在三维空间作有规则排列的图形。

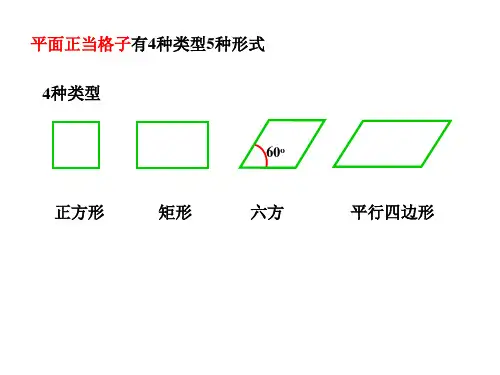
整个空间点阵就被这些平行线分割成多个紧紧地排列在一起的平行六面体有缘学习更多驾卫星ｙｇｄ３０７６或关注桃报：奉献教育（店铺）单位平行六面体的 选取原则 3.大小原则体积最小 1 对称性原则应能反映空间点阵对称性 2 角度原则 直角关系尽可能多4 对称性规定夹角不为直角 结点间距最小的行列做棱，夹角最接近直角的平行六面体二维平面点阵的划分(A)具有L44P的平面点阵；(B)具有L22P的平面点阵单位平行六面体在空间点阵中，选取出来的能够符合这几条原则的平行六面体称为单位平行六面体；可以用三条互不平行的棱a、b、c和棱间夹角α、β、γ来描述，如下图所示。

点阵常数棱a、b、c和棱间夹角α、β、γ的大小称为点阵常数。

晶体的点阵常数十四种布拉维点阵（格子）简单（原始）点阵（格子）(P) 结点分布在角顶，每个点阵包含一个结点体心点阵（格子）（I）结点分布在角顶和体心，每个点阵包含二个结点十四种布拉维点阵（格子）面心点阵（格子）(F) 结点分布在角顶和面心，每个点阵包含四个结点单面心点阵（格子）(A/B/C) 结点分布在角顶和一对面心，每个点阵包含2个结点根据布拉维推导，从一切晶体结构中抽象出来的空间点阵，按上述原则来选取平行六面体，只能有14种类型，称为14种布拉维点阵。

十四种空间点阵正交P(简单) C(底心) I(体心) F(面心) 点阵常数 a ≠ b ≠ cα= β= γ= 90°立方简单立方(P) 体心立方（I）面心立方（F）点阵常数 a =b =cα= β= γ= 90°如图立方为什么没有底心呢？假如有底心，将破坏立方的3L 4的对称性，只有1L 4。

立方三方（R ） 90120≠<====γβαc b a 点阵常数：六方（H ）12090===≠=γβαcb a 点阵常数： 四方（P ） 四方（I ）90===≠=γβαc b a 点阵常数：四方也不可能有底心，假如有，则破坏了“点阵点最少”的条件，还可画出只有一个点阵点的格子。

结构化学第七章课件

结构化学第七章课件


Laue方程的推导
a (cos －cos0 )= h h为整数 即在入射角为0 时，在方向产
生衍射。
直线点阵上衍射圆锥的形成
Laue 方程组： 对于空间点阵，应同时满足以下三式，
h、k、l为整数(但并不都是互质整数)－－衍射指标。
Laue 方程把衍射方向和晶胞参数联系在一起。
Laue方程组决定了衍射方向的分立性，因为空间点阵的 衍射方向是以三个互不平行的直线点阵为轴的的三组圆 锥面的共交线，所以只有某些特定方向上才会出现衍射。
h k l=nh* nk* nl* 才能产生反射。 如果某一晶面(h*k*l*)产生n级衍射，则可把其看作是晶 面(nh*nk*nl*)的一级衍射。晶面(h*k*l*)的面间距为d， 则晶面(nh*nk*nl*)的面间距就是d/n，于是Bragg方程可 写成：
2 (dh*k*l*)/n sinn = 即：2 dhkl sin =
d hkl
a h2 k2 l2
正交晶系
dh*k*l*
1 ( h* )2 ( k )2 (l )2
abc
六方晶系
dh*k*l*
1
4( h*2
hk 3a2
k
2
)
l 2 c2
Bragg方程表明，晶面指标为(h*k*l*)的晶面只对某些
角的入射线产生反射。可以证明，对于这些晶面，只有 衍射方向hkl和晶面指标(h*k*l*)满足：
1. 宏观对称元素和对称操作 晶体的理想外形在宏观表现出来的对称性
对称元素 旋转轴 (n或n) 反映面 (m) 对称中心 (i)
反轴 ( n )
对称操作
旋转 L() =2/n
反映 M 反演 I
旋转反演L()I
固体物理第二章第二节 对称性和布拉维格子的分类

固体物理第二章第二节 对称性和布拉维格子的分类

显然n=1,相当于不动操作(元素)E, n=2,3,4,6的转轴分别称为二度、三度、四度、 六度转轴
晶体的对称性定律的证明
B
A
如图,A为格点,B为离A最近 a a 的格点之一,则与 AB 平行的 格点之间的距离一定是 AB A a B 的整数倍。 如果绕A转角,晶格保持不变(对称操作).则 该操作将使B 格点转到 B位臵,则由于转动对称 操作不改变格子,在 B 处必定原来就有一个格点。 因为B 和A 完全等价,所有旋转同样可以绕B 进行. 由此可设想绕B 转角，这将使A 格点转到 A的 位臵。同样 A处原来也必定有一个格点
A B H E
D
D
C G
F
C
正四面体既无四 度轴也无对称心
参考方俊鑫书 P37-39
A
G
B F E H
旋转反演对称操作中只有4度 旋转反演对称操作是独立的 独立的对称操作有8种, 即1，2，3，4，6，i， m， 4 。 或C1，C2，C3， C4，C6 ，Ci，Cs，S4。
3
4
1830年，赫塞耳(Johann Friedrich Christian Hessel)首先导出了32种点群，由32种点群出发， 可以对布拉维点阵进行分类，这正是1850年布 拉维所作的工作，他证明了只有7个晶系。(点 群不含平移对称操作，因为平移导致任何格点 都要动，而点群必须至少有一个格点不动) 熊夫利(Schoenflies1891)和费奥多罗夫 (Fedorove 1892) 为了研究复式晶格(几套简单 格子的平移)的分类，考虑了平移对称操作， 提出了空间群的概念,并证明只有230种独立 的空间群。 可由此证明只有14种三维布拉维 点阵
nm
n2 n2
nm
对称性和布拉维格子的分类

对称性和布拉维格子的分类


群论作为数学的分支，是处理有一定对称性 的物理体系的有力工具，可以简化复杂的计算， 也可以预言物理过程的发展趋势，还可以对体 系的许多性质作出定性的了解。 群及其表示理论是物理系研究生的一门重要 基础课，对于本科生不作要求。因此，我们不 打算在这里讲过多的群论的知识。只是简单介 绍一下，让大家对群的概念有一个认识。 一、群的知识简介 1. 群的定义 ts)或操 作的集合，常用符号 G 来表示。
Ai Aj Ak , i j or i j
2). 群中一定包含一个不变元素(单位元素) E E G, EAi Ai E Ai 3). 存在逆元素 Ai G, Ai1 Ai Ai1 Ai1 Ai E
4). 满足组合定则
( Ai Aj ) Ak Ai ( Aj Ak )
因为B 和A 完全等价,所有旋转同样可以绕B 进行. 由此可设想绕B 转角，这将使A 格点转到 A的 位臵。同样 A处原来也必定有一个格点
显然n=1,相当于不动操作(元素)E, n=2,3,4,6的转轴分别称为二度、三度、四度、 六度转轴
晶体的对称性定律的证明
B
A
如图,A为格点,B为离A最近 a a 的格点之一,则与 AB 平行的 格点之间的距离一定是 AB a B A 的整数倍。 如果绕A转角,晶格保持不变(对称操作).则该 操作将使B格点转到B’ 位臵,则由于转动对称操作 不改变格子,在 B’ 处必定原来就有一个格点。
在晶体的几何对称性的研究中，每一个能 使晶体复原的对称操作，都满足上述群中的 元素的要求，由这些元素(或操作)所构成的 群叫对称性群(symmetry group),包括点群 (point group)和空间群(space group)
1830年，赫塞耳(Johann Friedrich Christian Hessel)首先导出了32种点群，由32种点群出发， 可以对布拉维点阵进行分类，这正是1850年布 拉维所作的工作，他证明了只有7个晶系。(点 群不含平移对称操作，因为平移导致任何格点 都要动，而点群必须至少有一个格点不动) 熊夫利(Schoenflies1891)和费奥多罗夫 (Fedorove 1892) 为了研究复式晶格(几套简单 格子的平移)的分类，考虑了平移对称操作， 提出了空间群的概念,并证明只有230种独立 的空间群。 1850年布拉维由此证明只有14种 三维布拉维点阵
2.2.4 晶体的14种Bravais格子简介

2.2.4 晶体的14种Bravais格子简介


a b c， 90 0
格点有两种分布方式：其一，分布于惯用元胞的八个顶点上；
其二，除顶点外，还分布于面心（0，1/2，1/2）和（1，1/2，1/2）
或（1/2，0，1/2）和（1/2，1，1/2）
有 两种 Bravais 格子：分
别称为简单单斜Bravais格子、底心单斜Bravais格子
背景音乐：
5°六方（Hexagonal）晶系或六角晶系
Bravais格子之惯用元胞的几何特征为：
a b c， 90 0 ， 120 0 有 格点的分布方式只有一种：分布于惯用元胞的八个顶点上 一种Bravais格子，称为简单六方
Bravais格子 Pearson 记法 hP， 平行六面体元胞不能显示出点对 称性，常选用正六方棱柱体作为
背景音乐：
4°四方(Tetragonal) 晶系或正方晶系或四角晶系 Bravais格子之惯用元胞的几何特征为：
a b c， 90 0
格点有两种分布方式：其一，分布于惯用元胞的八个顶点上；
有 其二，除顶点外，还分布于体心 两种Bravais格子，分别称
为简单四方Bravais格子和体心四方Bravais格子 Pearson 记法 tP 和tI，惯用元胞分别如图2.2.2－1中的（h）图和(i)图所示
Pearson 记法 mP、mA 或 mB ，惯用元胞分别如图 2.2.2－1中的（b）图、(c)图所
示。
背景音乐：
背景音乐：
3°斜方晶系或正交（Orthorhombic）晶系
Bravais格子之惯用元胞的几何特征为：
a b c， 900
格点有四种分布方式：其一，分布于惯用元胞的八个顶点 上；其二，除顶点外，还分布于体心；其三，除顶点外，还分 布于两个面心（0，1/2，1/2）和（1，1/2，1/2）或面心（1/2， 0，1/2）和（1/2，1，1/2）或面心（1/2，1/2，0）和（1/2， 1/2，1）；其四，除顶点外，还分布于六个面心 四种 有
-晶体结构的几何理论

-晶体结构的几何理论

Z
若行列经过坐标原点， 把该行列上距原点最近 的结点坐标x，y，z放在 “[ ]”内， [xyz]即为该行列的行 列符号。
X
[111]
Y
Crystallography
点的坐标 coordinates of point
空间格子中结点、行列符号的表示方法
图中粗实线及箭头表示行列方向，圆圈代表结点
质点
结点 （相当点）
立方面心格子
质点
NaCl晶胞
Crystallography
第8章 晶体结构的几何理论
Crystallography
第8章 晶体结构的几何理论
a
b
在一个晶胞中，反映了晶体结构中对称要素和 质点的种类及分布规律。 对一个晶胞进行分析，就可以知道整个晶体结 构中对称要素和质点分布规律。
第8章 晶体结构的几何理论
⑶各晶系单位平行六面体的形状
③斜方晶系 a≠b≠c α=β=γ=90°
c
β α a γ
b
斜方格子
CrystallographyΒιβλιοθήκη 第8章 晶体结构的几何理论
⑶各晶系单位平行六面体的形状
④单斜晶系 a≠b≠c α=γ=90° β ≠ 90°
c
β α γ a
b
单斜格子
Crystallography
有些格子类型与所在晶系的对称不符。 有些格子类型与空间格子的条件不符。 有些格子类型可以被改划为其它格子。
因此，只有14种空间格子，也叫14种布拉维格子。 （A.Bravis于1848年最先推导出来的）

十四种空间格子
举例说明：
1、四方底心格子可转变为体积更小的四方原
始格子 ；
2、在等轴晶系中，若在立方格子中的一对面
十四种布拉菲格子

十四种布拉菲格子

晶体的十四种Bravais Bravais格子简介 §1.2.6 晶体的十四种Bravais格子简介
就目前所知，晶体多达20000多种以上，它们的几何 就目前所知，晶体多达 多种以上， 多种以上 外形更是多姿多彩、精美绝伦、奥妙无比， 外形更是多姿多彩、精美绝伦、奥妙无比，足以让所有 的能工巧匠叹为观止！然而，种类繁多、 的能工巧匠叹为观止！然而，种类繁多、形状各异的晶 体在微观结构的周期性特征上却是极其简单的， 体在微观结构的周期性特征上却是极其简单的，描述晶 体微观结构周期性特征的Bravais格子总共只有十四种不 格子总共只有十四种不 体微观结构周期性特征的 格子总共只有十四种 同的类型。 同的类型。
Pearson记法 →
hR
7°立方(Cubic) 晶系 立方(Cubic) Bravais格子之惯用元胞的几何特征为： Bravais格子之惯用元胞的几何特征为： 格子之惯用元胞的几何特征为
a = b = c，α = β = γ = 90 0
格点有三种分布方式：其一，分布于惯用元胞的八个顶点上； 格点有三种分布方式：其一，分布于惯用元胞的八个顶点上； 其二，除顶点外，还分布于体心；其三，除顶点外，还分布于六 其二，除顶点外，还分布于体心；其三，除顶点外， Bravais格子 简单立方Bravais格子、 个面心 有 三种Bravais格子，分别称为简单立方Bravais格子、 → 三种Bravais格子，分别称为简单立方Bravais格子 体心立方Bravais格子和面心立方Bravais格子 体心立方Bravais格子和面心立方Bravais格子 Bravais格子 Bravais cP、 cP Pearson记法 → 、
cI和cF，惯用元胞分别如图1.2.6－ 中的（ cI和cF，惯用元胞分别如图1.2.6－1中的（l）图、(m)图和（n） 1.2.6 (m)图 图所示 背景音乐： 背景音乐：
《结晶学》第7章晶体结构的基本特征

《结晶学》第7章晶体结构的基本特征

注意：螺旋轴ns的下标s是以右旋的螺距来标定的。
（1 2）T 3
2T T
3
规定：
①在螺旋轴的符号中，若s<1／2n为右旋螺旋轴。 例如，31，4l，62。
②在螺旋轴的符号中，若s>1/2n者为左旋螺旋轴。 例如，32，43，64，65。
③当s=1/2n者为中性螺旋轴。例如，21，42和63。
βα γ
2、各晶系平行六面体的形状和大小
说明：六方晶系的格子类型
3、平行六面体中结点的分布
四种格子类型 a、原始格子；b、c、d 、底心格子； e 、体心格子；f 、面心格子；
4、14种布拉维格子
为什么只有14种布拉维格子？ （1）某些类型的格子彼此重复并可转换 （2）某些格子不符合晶系的对称特点
2．线缺陷
线缺陷是指：在晶体内部结构中沿某条线(行列) 周围局部范围内所产生的晶格缺陷。
它的表现形式主要是位错。
位错是指晶体在应力作用下，晶格中的一部分沿 一定的面网相对于另一部分的局部滑动，滑移与未滑 移部分的分界处出现了质点错乱排列。滑移与未滑移 部分的分界线称为位错线。
位错主要有两种类型：刃位错和螺旋位错
刃位错的晶格示意图
螺旋位错的晶格示意图
刃位错
螺位错
3．面缺陷
面缺陷是指沿晶格内或晶粒间某些面的 两侧局部范围内所出现的晶格缺陷。
堆垛层错
晶体结构中互相平行的堆积层有其固有的重复排 列顺序。如果堆垛层偏离了原来固有的顺序．则视为产 生了堆垛层错。
畴界壁
在晶体结构中， 某个局部区域与 周围区域在某种 性质上存在不连 续现象时，此区 域称为晶畴；相 邻晶畴之间的界 面称为畴界壁。
晶胞参数（a、b、c、 α、β、γ）
14种布拉维点阵的结构特征

14种布拉维点阵的结构特征

14种布拉维点阵的结构特征布拉维点阵是描述晶体中原子、离子或分子排列方式的一种数学模型。

有14种布拉维点阵，也被称为14种布拉维格子或14种布拉维空间群。

这些点阵通过特定的对称性元素来定义。

以下是这些14种布拉维点阵的主要结构特征：1三立方格子（Triclinic）：没有垂直平面或轴的对称性。

所有晶胞边长和角度均可不同。

2单斜格子（Monoclinic）：有一个垂直平面。

一个轴有对称性。

3正交格子（Orthorhombic）：三个垂直的平面和三个垂直的轴。

所有晶胞角度均为90度。

4四方格子（Tetragonal）：一个垂直平面和一个垂直轴。

所有晶胞边长相等，两个轴长度相等。

5六方格子（Hexagonal）：六重对称性轴，垂直于平面。

六边形的基本晶胞。

6立方格子（Cubic）：三个垂直平面和三个垂直轴。

所有晶胞边长相等，所有角度均为90度。

7三斜半基心格子（Triclinic P）：没有垂直平面或轴的对称性。

所有晶胞边长和角度均可不同。

8单斜面心格子（Monoclinic P）：有一个垂直平面。

一个轴有对称性。

9正交面心格子（Orthorhombic P）：三个垂直的平面和三个垂直的轴。

所有晶胞角度均为90度。

10四方面心格子（Tetragonal P）：一个垂直平面和一个垂直轴。

所有晶胞边长相等，两个轴长度相等。

11六方面心格子（Hexagonal P）：六重对称性轴，垂直于平面。

六边形的基本晶胞。

12立方面心格子（Cubic P）：三个垂直平面和三个垂直轴。

所有晶胞边长相等，所有角度均为90度。

13三斜体心格子（Triclinic I）：没有垂直平面或轴的对称性。

所有晶胞边长和角度均可不同。

14正交体心格子（Orthorhombic I）：三个垂直的平面和三个垂直的轴。

所有晶胞角度均为90度。

这些布拉维点阵描述了晶体的结构特征，是研究材料科学和晶体学的重要工具。

14种布拉维格子及堆积方式


2.3.4 思考题
• 1. 什么是布拉维格子？试指出14种布拉 维格子的特征。 • 2. 等大球体的紧密堆积有几种形式？并 指出相应的空隙情况。
最紧密堆积的方式有两种，一是六 方最紧密堆积（Cubic closest packing， 缩写为CCP），最紧密排列层平行于 {0001}，可以用ABABAB……顺序来表 示（图2-3-2）。另一种是立方最紧密堆 积（Hexagonal closest packing，缩写为 HCP），最紧密排列层平行于{111}，可 以用ABCABCABC……顺序来表示（图 2-3-3）。自然铜、自然金、自然铂等矿 物的晶体结构属立方最紧密堆积方式， 而锇铱矿以及金属锌等晶体的结构属六 方最紧密堆积方式。
符合对称特点和选择原则的格子共有7 种类型，共计14种不同型式的空间格子， 即通常所称的十四种布拉维格子（the fourteen Bravais space lattices），如图2-31所示。布拉维格子是空间格子的基本组成 单位，只要知道了格子形式和单位平行六 面体参数后，就能够确定整个空间格子的 一切特征。
2.3 14种布拉维格子和球体 紧密堆积
2.3.1 实验目的
• 加深对14种布拉维格子和球体紧密堆积 原理的理解。
2.3.2 基本原理
1. 布拉维格子 只在单位平行六面体的八个角顶上分布有 结点的空间格子，称为原始格子 （Primitive lattice,符号P），在单位平行 六面体的体中心还有一个结点时，则构 成体心格子（Body-centered lattice，符 号I）。
三方菱面体
C:与本晶系 对称不符
I=P F=P
简单四方
C=P
体心四方
F=I
简单立方

14种布拉维格子


14种布拉维格子之八：正交简单（oP)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之九：正交体心（oI)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十：正交C心 oC(或 oA, oB）
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十一：正交面心（oF)
请
都是点阵点.黑点
点
与蓝线表示一个
击
正当格子
按
钮
打
开
布拉维格子之七：三方晶系的六方R 心(hR)
请 点 击 按 钮 打 开 晶 格 模 型
三方晶系的六方简单 (hP)
请点击按钮打开晶格模型
六方简单 (hP)格子已用于六方晶系, 现在又可用于三方晶系, 所以只算一种格子. 尽管三方晶系的两种格子------六方简单(hP)和六方R 心(hR)------形状都与六方 晶系的六方简单 (hP)格子相同（即hR是两个晶系共用的）, 但真实的三方晶体中只 有三次对称轴而没有六次对称轴, 六方晶体才有六次对称轴.
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十二：单斜简单（mP)
请点击按钮打开晶格模型
14种布拉维格子之十三：单斜C心（mC)
请点击按钮打开晶格模型
14种布拉维格子之十四：三斜简单 (aP)
请点击按钮打开晶格模型
为什么要考虑带心格子?
立方面心格子，若按左图取素格子只能表现三方对称性；若取右图 所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖)：
请点击按钮观察动画
请点击按钮打开晶格模型
14种布拉维格子之一：立方简单（cP）

布拉维格子

定义
晶体的基本性质和外形规律特征的根本原因在于它内部的空间格子构造，在理想晶体中，其内部质点均按照格子构造规律排列。

平行六面体是空间格子的最小单位，整个晶体结构可视为平行六面体（即晶胞）在三维空间平行的、毫无间隙的重复堆砌而成。

晶体的空间格子可分为以下四种类型
1、原始格子（P）：结点分布于平行六面体的八个角顶上。

2、底心格子：结点分布于平行六面体的角顶及某一对面的中心。

其中又可细分为三种类型：
①、C心格子（C）：结点分布于平行六面体的角顶和平行（001）一对平面的中心；
②、A心格子（A）：结点分布于平行六面体的角顶和平行（100）一对平面的中心；
③、B心格子（B）：结点分布于平行六面体的角顶和平行（010）一对平面的中心。

一般情况下所谓底心格子即为C心格子，对A心或B心格子，能转换成C心格子时，应尽可能地予以转换。

3、体心格子（I）：结点分布于平行六面体的角顶和体中心。

4、面心格子（F）：结点分布于平行六面体的角顶和三对面的中心。

十四格子
按晶系的不同，空间格子具以下十四种类别：
晶系原始格子（P）底心格子（C）体心格子（I）面心格子（F）
三斜三斜原始C=I I=F
F=P
单斜单斜原始单斜底心I=F
F=C
斜方斜方原始斜方底心斜方体心
斜方面心
四方四方原始C=P四方体心
F=I
三方三方原始与本晶系对称不符I=F
F=P
六方六方原始与本晶系对称不符与空间格子的条件不符与空间格子的条件不符
等轴等轴原始与本晶系对称不符等轴体心等轴面心。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
下载
正交体心格子（P）
属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为：a0 ≠ b0 ≠ c0 α=β=γ=90°
下载
正交底心格子（Q）
属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为：a0 ≠ b0 ≠ c0 α=β=γ=90°
下载
正交面心格子（S）
下载
四方原始格子（T）
属于四方晶系，单位平行六面体为横截面为正方形的四方柱。规定柱面相交的棱c0，单位平行六面体参数为：a0 = b0 = c0 α=β=γ= 90°
下载
四方体心格子（U）
属于四方晶系单位平行六面体为横截面为正方形的四方柱。规定柱面相交的棱c0，单位平行六面体参数为：a0 = b0 = c0 α=β=γ= 90°
下载
三斜原是格子（Z）
单斜平行六面体是三条棱不相等，三对面互相间不垂直的斜平行六面体。单位平行六面体参数为：a0 ≠ b0 ≠ c0，α≠β≠γ≠900
下载
单斜原始格子（M）
单位平行六面体的三对面中有两对是矩形，另一对是非矩形。两对矩形平面都垂直于非矩形平面，而它们之间的夹角为β，但∠β≠90°。a0≠b0≠c0，α=γ=90°，β≠90°
下载
立方和三方原始格子(H)
对应于六方晶系的空间六方格子。单位平行六面体底面为菱形的柱体。菱形交角为60o和120 o，如果把三个单位平行六面体拼起来，底面就成六边形，柱面的交棱就是六次轴方向。单位平行六面体参数为：a0≠b0≠c0，α=β=90 o，γ=120 o
下载
三方菱面体格子（R）
属于三方晶系，单位平行六面体相当于立方体在4L3中的一个L3方向被拉长或压缩，使立方体变成菱面体。单位平行六面体参数为：a0 = b0 = c0 α=β=γ≠90°、60°、109°28′16″
属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为：a0 ≠ b0 ≠ c0 α=β=γ=90°
下载பைடு நூலகம்
立方体心格子（B）
属于等轴晶系，单位平行六面体是一个立方体。单位平行六面体参数为：a0 = b0 = c0 α=β=γ= 90°
下载
立方面心格子(F)
属于等轴晶系，单位平行六面体是一个立方体。位平行六面体参数为：a0 = b0 = c0 α=β=γ= 90?
下载
立方原始格子
属于等轴晶系，单位平行六面体是一个立方体。单位平行六面体参数为：a0 = b0 = c0 α=β=γ= 90
下载
十四种不拉维格子
类型
说明
下载动画
单斜底心格子（N）
单位平行六面体的三对面中有两对是矩形，另一对是非矩形。两对矩形平面都垂直于非矩形平面，而它们之间的夹角为β，但∠β≠90。。a0≠b0≠c0，α=γ=90。，β≠90。
下载
正交原始格子（O）
属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为：a0 ≠ b0 ≠ c0 α=β=γ=90°