湖北省当阳市第一高级中学2019届高三数学9月月考试题文

2019学年度高三第一学期9月考数学（文）试题(时间：120分钟 满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1.已知向量,a b =2,=2a b ，且()-a b a ⊥，则向量a 和b 的夹角是 A.4πB.2πC.34πD. π 2按数列的排列规律猜想数列2468,,,3579--，…的第10项是（ ）A. 1617-B. 1819-C. 2021-D. 2223-3.等比数列{a n }中，a 1=18，q =2，则a 4与a 8的等比中项是（ ）A.±4B.4C.±14D. 144若数列{a n }的通项公式是(1)(32)nn a n =--，则1210a a a ++=L ( )A.30B.29C.﹣30D.﹣295平面向量a b 与r r 的夹角为()2,0,123a b a b π==-=，，则rr r rA.B.0D.26复数121iz i-=-（i 为虚数单位）在复平面上对应的点位于 A.第一象限 B.第二象限C.第三象限D.第四象限7在平行四边形ABCD 中，对角线AC 与BD 交于点O ，()CO AB AD λ=+，则实数λ=( ) A ．12-B ．12C ．-2D ．2 8若等差数列{}n a 的前7项和721S =，且21a =-，则6a = A.5B.6C.7D.89等边三角形ABC 的边长为1，,,BC a CA b AB c ===，那么a b b c c a ++等于（A ）3 （B ）－3 （C ）32 （D ）－3210数列{a n }的前n 项和为S n ，若a n =1(1)n n +，则S 10等于（ ）A.1B.1011 C. 111D. 111011.已知ABC ∆的重心为G ，角A ，B ，C 所对的边分别为,,a b c ，若2330a G A b G B c G C ++=，则si n :si n:si n A B C =A.1：1:1B. 3:2 2:1 212如右图，在4,30,ABC AB BC ABC AD ∆==∠=o中，是边BC 上的高，则AD AC ⋅uuu r uuu r的值等于A.0B.4C.8D. 4-第Ⅱ卷 （非选择题 共90分）二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中的横线上) 13已知复数z 满足()12z i i ⋅-=+，其中i 为虚数单位，则z 的共轭复数是_________14.数列{a n }满足a 1+3a 2+32a 3+…+3n -1a n =3n，则数列{a n }的通项公式为 __15已知△ABC 的面积为2，在△ABC 所在的平面内有两点P Q 、，满足0,2PA PC QA BQ +==，则APQ ∆的面积为16若两个等差数列{a n }和{b n }的前n 项和分别是S n ，T n ，已知n n S T =55n n +，则1011912813a ab b b b +=++ ___ ___ ．三、解答题(本大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17已知ABC ∆的角A 、B 、C 的对边分别为a 、b 、c ，若向量) , 2(c b a m -=与)cos , (cos C B n =共线．（Ⅰ）求角C 的大小；（Ⅱ）若2| |2| |==n m ，求a 的大小．18.已知数列{a n }的通项为a n ，前n 项和为s n ，且a n 是s n 与2的等差中项，数列{b n }中，b 1=1，点P （b n ，b n +1）在直线x -y +2=0上． 求数列{a n }、{b n }的通项公式19.已知向量(cos ,1sin ),(cos ,sin )()m n R ααααα=-=-∈ （1)若m n ⊥，求角α的值； （2）若||3m n -=，求sin α的值20在各项均为正数的等比数列{}n a 中，1231, 6.a a a =+= （Ⅰ）求数列{}n a 的的通项公式；（Ⅱ）若21,,n n n n b a n -⎧=⎨⎩为奇数，为偶数，求数列{}n b 的前n 项和.n T21 已知数列{}n a 是公差不为零的等差数列，其前n 项和为n S ，满足25225=-a S ，且1341,,a a a 恰为等比数列{}n b 的前三项.（I ）求数列{}n a ，{}n b 的通项公式； （II ）设n T 是数列⎭⎬⎫⎩⎨⎧+11n n a a 的前n 项和，是否存在+∈N k ,使得n nb T 121=-成立，若存在，求出k 的值；若不存在，说明理由。

2019高三数学9月月考试题 文一：选择题：（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中， 只有一项）1、设复数z 1，z 2在复平面内的对应点关于虚轴对称，z 1＝2＋i ，则z 1z 2＝( ) A ．－5 B ．5 C ．－4＋i D ．－4－i2、设集合A ＝{x ||x －1|<2}，B ＝{y |y ＝2x，x ∈[0，2]}，则A ∩B ＝( ) A ．[0，2] B ．(1，3) C ．[1，3) D ．(1，4) 3. z 是z 的共轭复数，若()2,2(z z z z i i +=-=为虚数单位），则z =（ ）A ．1i +B ．1i --C ．1i -+D ．1i -4. 已知=U R ，函数)1ln(x y -=的定义域为M ，}0|{2<-=x x x N ，则下列结论正确的是（ ） A ．MN M = B ．()U MC N U = C ．φ=⋂)(N C M UD ．N C M U ⊆5、已知命题p ：∀x >0，总有(x ＋1)e x>1，则⌝p 为 ( )A ．∃x 0≤0，使得(x 0＋1)0e x≤1 B ．∃x 0>0，使得(x 0＋1)0e x≤1 C ．∀x >0，总有(x ＋1)0e x≤1 D ．∀x ≤0，总有(x ＋1)0e x ≤1 6、已知下列命题：( ) （1）“c o s0x <”是“tan 0x <”的充分不必要条件；（2）命题“存在,41x Z x ∈+是奇数”的否定是“任意,41x Z x ∈+不是奇数”； （3）已知,,,a b c R ∈若22,ac bc >则.a b > 其中正确命题的个数为 A. 0 B. 1 C. 2 D. 37、如果实数满足不等式组，目标函数的最大值为6，最小值为0，则实数k 的值为（ ） A. 1 B. 2 C. 3 D. 4 8（0ω>），当ω取最小值时，以下命题中假命题是（ ） A ．函数()f x 的图象关于直线B 是函数()f x 的一个零点C. 函数()f x 的图象可由D ．函数()f x 在9、若a>b>1,0<c<1，则( ) A. a c<b cB. ab c<bacC. a log b c<b log a cD. log a c<log b c10、若函数()f x 是定义在R 上的奇函数，且当0x >时，21()log (1),1f x x x =-++则不等式4(1)7f x +>的解集为( )A. (2,)+∞B. (,1)(3,)-∞-⋃+∞C. (4,2)-D. (,4)-∞-11. 若点(),P a b 在函数23ln y x x =-+的图象上，点(),Q c d 在函数2y x =+的图象上，则()()22a cb d -+-的最小值为（ ）A ．B ． 2C ．D ．812.设函数()f x 的定义域为R , ()()()(),2f x f x f x f x -==-, 当[]0,1x ∈时,()3f x x =, 则函数()()()cos g x x f x π=-在区间15,22⎡⎤-⎢⎥⎣⎦上的所有零点的和为（ ） A.7 B. 6 C.3 D.2 二、填空题（每题5分，满分20分） 13.已知不等式220ax bx ++>的解集为则a b +的值为________． 14：在ABC ∆中，111,2,4,,,2224A AB AC AF AB CE CA BD BC π∠======，则DE DF 的值为 ．15．已知0,0a b >>，若不等式恒成立，则m 的最大值为_________． 16.已知函数ln ,0,()ln(),0.x x x f x x x x -- >⎧=⎨--+<⎩ 则关于m 的不等式11()ln 22f m <-的解集为 。

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……2019学年度上学期高三九月月考数学（文）试题时间：120分钟 满分：150分第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题列出的四个选项中，选出符合题目要求的一项）1.已知点(0,1),(3,2)A B ，向量(4,3)AC =--，则向量BC =（ ） A. (7,4)-- B.(7,4) C. (1,4)- D .(1,4) 2．函数y ＝－x 2－3x ＋4x的定义域为( )A ．[－4,1]B ．[－4,0)C ．(0,1]D ．[－4,0)∪(0,1]3．若点(sin 5π6，cos 5π6)在角α的终边上，则sin α的值为( )A ．－32 B ．－12 C ．12 D ．324．命题P ：∃x >0，x ＋1x＝2，则P ⌝为( )A ．∀x >0，x ＋1x ＝2B ．∀x >0，x ＋1x ≠2C ．∀x >0，x ＋1x≥2 D ．∃x >0，x ＋1x≠25.已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩ ，且()3f a =-，则(6)f a -=（ ）A. 74-B. 54-C. 34- D .14-6．已知函数)(x f 的导函数为)(x f '，且满足x ln )1(2)(+'=f x x f ，则)1(f '等于( )A ．－eB ．－1C ．1D ．e7．函数y ＝2sin(π3－2x )的单调递增区间为( )A ．[－π12＋k π，5π12＋k π](k ∈Z )B ．[5π12＋k π，11π12＋k π](k ∈Z )C ．[π6＋k π，2π3＋k π](k ∈Z )D ．[－π3＋k π，π6＋k π](k ∈Z )8．已知函数f (x )＝ax 2＋(a －3)x ＋1在区间[－1，＋∞)上单调递减，则实数a 的取值范围是( )A ．[－3,0)B ．(－∞，－3]C ．[－2,0]D ．[－3,0]9．已知函数f (x )＝ln x ＋ln(2－x )，则( )A ．f (x )在(0,2)上单调递增B ．f (x )在(0,2)上单调递减C ．y ＝f (x )的图象关于点(1,0)对称D ．y ＝f (x )的图象关于直线x ＝1对称 10．已知函数f (x )是定义在(－∞，＋∞)上的奇函数，若对于任意的实数x ≥0，都有f (x ＋2)＝f (x )，且当x ∈[0,2)时，f (x )＝log 2(x ＋1)，则f (－2 017)＋f (2 018)的值为( ) A ．－1 B ．－2 C ．2D ．111．如果函数y ＝f (x )的导函数的图象如图所示，给出下列判断： ①函数y ＝f (x )在区间(－3，－12)内单调递增；②函数y ＝f (x )在区间(－12，3)内单调递减；③函数y ＝f (x )在区间(4,5)内单调递增； ④当x ＝2时，函数y ＝f (x )有极小值； ⑤当x ＝－12时，函数y ＝f (x )有极大值．则上述判断中正确的是( )A ．①②B ．②③C ．③④⑤D ．③ 12．设函数()323e 622e 2xx f x x x x a x ⎛⎫=+-+-- ⎪⎝⎭，若不等式()0f x ≤在[)2,-+∞上有解，则实数a 的最小值为（ ） A ．312e -- B ．3142e -- C ．322e-- D ．11e --第II 卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分。

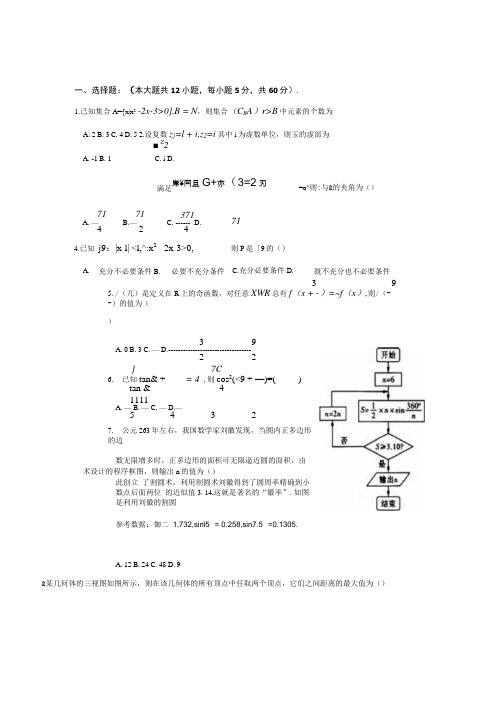
一、选择题：（本大题共12小题，每小题5分，共60分）.1.己知集合A={x|x 2 -2x-3>0],B = N ，则集合（C R A ）r>B 中元素的个数为A. 2B. 3C. 4D. 5 2.设复数z }=l + i,z 2=i 其中i 为虚数单位，则玉的虚部为■ Z 23 95. /（兀）是定义在R 上的奇函数，对任意XWR 总有f （x + -）=~f （x ）,则/（--）的值为（）3 9 A. 0 B. 3 C. — D. ---------------------------------- 2 2]7C 6.已知tan& + ------ = 4 ,则cos 2(<9 + —)=( ) tan & 4 1111 A. — B. — C. — D.— 5 4 3 2 7. 公元263年左右，我国数学家刘徽发现，当圆内正多边形的边数无限增多时，正多边形的面积可无限逼近圆的面积，由此创立 了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位 的近似值3. 14,这就是著名的“徽率”.如图是利用刘徽的割圆参考数据：御二 1,732,sinl5° = 0.258,sin7.5° =0.1305.A. 12B. 24C. 48D. 9&某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的最大值为（） A. -1 B. 1 C. i D.满足 岸¥冃且G+亦（3=2刃 =o^则:与&的夹角为（）71 71 A. — B.— 4 2 4.已知 j9：|x-l| <l,^:x 2 - 2x-3>0, 371 C. ------ D. 4 71则P 是「9的（）A. 充分不必要条件B. 必要不充分条件C.充分必要条件D.既不充分也不必要条件 术设计的程序框图，则输出n 的值为（）9. 设有下面四个命题：① “若a>0,则:与忌与的夹角为锐角”及它的逆命题均为真命题② 若 R,2X > 0,则—\p : 3x 0 e R,2X ° < 0③ “ ab<l ”是“ Q W1或b<l ff 的充分不必要条件④ 命题“ AABC 中，若A>B ,则sin A > sin B "的逆命题为真命题其中正确命题的个数是（）A. 3B. 2C. 1D. 010. 已知定义在7?上的函数/（x-1）的图像关于兀=1对称，且当兀〉0时，/（兀）单调递减，若 a = f(logQ 5 3),Z? = /(0.5-13),c = /(0.76)则 a.b.c 的大小关系是()二、填空题：（本大题共4小题，每小题5分，共20分）.14.在正方体ABCD-A.B.C.D.中，对角线AC ；与底面ABCD 所成角的正弦值为.侧视图A . c> a> bB . b> a> c c. a> c>b D . c>b> a 又AD DC = 0,则BD 的最大值为（ D . 2A /212.己知函数y (x ) = -- — ax' XX e （0,+8）,当%2 >%!时，不等式丿凶 无2 也。

湖北省 高三9月月考数学(文)试卷本试题卷共4页，三大题24小题。

全卷满分150分，考试用时120分钟。

★祝考试顺利★★注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效.3. 回答第Ⅱ卷时，将答案写在答题卡上，答在本试题上无效.第Ⅰ卷一、选择题（每小题5分，共60分）1、已知33(23)i z i -=⋅-，那么复数z 在平面内对应的点位于 （ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2、已知向量(1,)a n =r ，(1,)b n =-r ，若a b ⊥r r，则a =rA ．1B ．2C ．2D ．43、将函数sin(2)3y x π=-的图象先向左平移6π，然后将所得图象上所有点的横坐标变为 原来的2倍（纵坐标不变），则所得到的图象对应的函数解析式为 A ．cos y x =- B ．sin 4y x =C ．sin()6y x π=-D ．sin y x =4、下列命题中，真命题是 A ．0x R ∃∈，使得00x e≤ B ．函数2()2x f x x =-有两个零点 C ．0a b +=的充要条件是1ab=- D ．1,1a b >>是1ab >的充分不必要条件5、若01,x y <<<则下列不等式成立的是A. 11()()22x y <B. 1133x y --< C. 11log log 22x y < D. log 3log 3x y <6、已知sin cos 2αα-=，(0,)απ∈，则tan α=A ．－1B ．－22 C.22D ．1 7、函数1xy a a=-(0a ≠，且1a ≠)的图象可能是( )8、已知()f x 是定义在R 上的奇函数，当0x ≥时，2()3f x x x =-.则函数()()3g x f x x =-+的零点的集合为A ．{}1,3B ．{}3,1,1,3--C ．{}27,1,3-D ．{}27,1,3--9、若1sin()63πα-=，则2cos(2)3πα+=A ．13- B. 79- C. 79D. 1310、定义在R 上的函数()f x 满足(6)()f x f x +=．当31x -≤<-时，2()(2)f x x =-+； 当13x -≤<时，()f x x =，则(1)(2)(3)(2012)f f f f ++++=L ( ) A ．335 B ．338 C ．1678 D ．201211、设O 为ABC ∆所在平面内一点．若实数,,x y z 满足0xOA yOB zOC ++=u u u r u u u r u u u r r，其中222(0)x y z ++≠,则“0xyz =”是“点O 在ABC ∆的边所在直线上”的A ．充分而不必要条件B ．必要而不充分条件 C.充要条件 D ．既不充分也不必要条件12、如图，已知直角三角形ABC ∆的三边AC BA CB ,,的长度成等差数列，点E 为直角边AB 的中点，点D 在斜边AC 上，且AC AD λ=， 若BD CE ⊥，则=λ A.177 B. 178 C. 179 D. 1710第Ⅱ卷本卷包括必考题和选考题两个部分。

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……2019届高三9月月考试卷高三文科数学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．三次函数()323212f x ax x x =-++的图象在点()()1,1f 处的切线与x 轴平行，则()f x 在区间()1,3上的最小值是（ ）A ．83B ．116C ．113 D ．532．已知()21i =1i z-+（i 为虚数单位），则复数z =（ ） A ．1i -- B ．1i - C ．1i -+ D ．1i +3．如表是我国某城市在2017年1月份至10月份个月最低温与最高温（C ︒）的数据一览表．已知该城市的各月最低温与最高温具有相关关系，根据这一览表，则下列结论错误的是（ ）此卷只装订不密封级 姓名 准考证号 考场号 座位号A ．最低温与最高位为正相关B ．每月最高温和最低温的平均值在前8个月逐月增加C ．月温差（最高温减最低温）的最大值出现在1月D ．1月至4月的月温差（最高温减最低温）相对于7月至10月，波动性更大4．等比数列{}n a 的前n 项和为n S ，且14a ，22a ，3a 成等差数列，若11a =，则4s =（ ） A ．7B ．8C ．15D ．165．已知函数()f x 为奇函数，且当0x >时，()210f x x x=+>，则()1f -=（ ） A ．2- B ．0 C ．1D ．26．执行如图所示的程序框图，如果输入的0.01t =，则输出的n =（ ） A ．5B ．6C ．7D ．87．已知集合2{20}P x x x =|-≥，}{12Q x x =|<≤，则()R C P Q =（ ） A ．[0,1) B ．(0,2] C ．(1,2) D ．[1,2]8．已知()2sin13,2sin77=︒︒a ，1-=a b ，a 与-a b 的夹角为3π，则⋅=a b （ ） A ．2B ．3C ．4D ．59．平面直角坐标系xOy 中，动点P 到圆()2221x y -+=上的点的最小距离与其到直线1x =-的距离相等，则P 点的轨迹方程是（ ） A ．28y x =B ．28x y =C ．24y x =D ．24x y =10．某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（ ） A ．2B ．4C．2D．4+11．设抛物线C ：24y x =的焦点为F ，过点()2,0-且斜率为23的直线与C 交于M ，N 两点， 则FM FN ⋅=（ ） A ．5B ．6C ．7D ．812．已知在正方体1111ABCD A B C D -中，点E 是AB 中点，点F 是11B C 中点，若正方体1111ABCD A B C D -的内切球与直线EF 交于点G ，H ，且3GH =，若点Q 是棱1BB 上一个动点，则1AQ D Q +的最小值为（ ） A ．6B．C．D． 第Ⅱ卷二、填空题：（本大题共4题，每小题5分，满分20分，将答案填在答题纸上） 13．设x ，y 满足约束条件1400x y x y x y -≥⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则3z x y =-的取值范围为__________．14．某学校有两个食堂，甲、乙、丙三名学生各自随机选择其中的一个食堂用餐，则他们在同一个食堂用餐的概率为__________．15．在数列{}n a 中，113a =，()113,3n n n n a a a ++=∈N +，且13n n b a =+．记12n n P b b b =⨯⨯⨯，12n n S b b b =+++，则13n n n P S ++=__________．16．已知平面直角坐标内定点()1,0A -，()1,0B ，()4,0M ，()0,4N 和动点()11,P x y ，()22,Q x y ，若1AP BP ⋅=，1122OQ t OM t ON ⎛⎫⎛⎫=-++ ⎪ ⎪⎝⎭⎝⎭，其中O 为坐标原点，则QP 的最小值是__________．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．（12分）在ABC △中，角A ，B ，C 所对的边分别是a ，b ，c ，且c o s c o s sin A B Ca b c+=． （1）证明：sin sin sin A B C =；（2）若22265b c a bc +-=，求tan B ．18．（12分）如图，在平行四边形ABCM 中，3AB AC ==，90ACM ∠=︒，以AC 为折痕将ACM △折起，使点M 到达点D 的位置，且AB DA ⊥．（1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且23BP DQ DA ==，求三棱锥Q ABP -的体积．19．（12分）某家庭记录了未使用节水龙头50天的日用水量数据（单位：3m）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：未使用节水龙头50天的日用水量频数分布表使用了节水龙头50天的日用水量频数分布表（1）在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图：（2）估计该家庭使用节水龙头后，日用水量小于30.35m 的概率；（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表．）20．（12分）已知中心在原点O ，左、右焦点分别为1F ，2F ，焦距为A ，B 是椭圆上两点．（1）若直线AB 与以原点为圆心的圆相切，且OA OB ⊥，求此圆的方程；（2）动点P 满足：3OP OA OB =+，直线OA 与OB 的斜率的乘积为13-，求动点P 的轨迹方程．21．（12分）已知函数()21e xax x f x +-=．（1）求曲线()y f x =在点()0,1-处的切线方程； （2）证明：当1a ≥时，()e 0f x +≥．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．（10分）【选修4-4：坐标系与参数方程】以直角坐标系xOy中，以O为极点，x轴非负半轴为极轴建立极坐标系，直线l的参数方程为x ty at =⎧⎨=⎩（t 为参数），曲线1C 的方程为()4sin 12ρρθ-=，定点()6,0A ，点P 是曲线1C 上的动点，Q 为AP 的中点．（1）求点Q 的轨迹2C 的直角坐标方程；（2）直线l 与曲线2C 相交于B ，C 两点，若BC ≥a 的取值范围．23．（10分）【选修4-5：不等式选讲】 已知函数()2f x x a x =++-．（1）当3a =时，求不等式()7f x ≥的解集；（2）若()4f x x ≤-的解集包含[]0,2，求a 的取值范围．高三文科数学答 案一、选择题． 1．【答案】D 2．【答案】A 3．【答案】B 4．【答案】C 5．【答案】A 6．【答案】C 7．【答案】C 8．【答案】B 9．【答案】A 10．【答案】C 11．【答案】D 12．【答案】C 二、填空题． 13．【答案】[]2,4- 14．【答案】1415．【答案】316．三、解答题．17．【答案】（1）见解析；（2）4．【解析】（1）根据正弦定理，可设(0)sin sin sin a b ck k A B C===>，则s in a k A =，sin b k B =，sin c k C =．代入cos cos sin A B Ca b c+=中，有cos cos sin sin sin sin A B C k A k B k C +=， 变形可得sin sin sin cos cos sin sin A B A B A B A B =+=+（）．在ABC △中，由A B C ++=π， 有sinsin sin A B C C +=π-=（）（），所以sin sin sin A B C =． （2）由已知，22265b c a bc +-=，根据余弦定理，有2223cos 25b c a A bc +-==．所以4sin 5A =．由（1），s i n s i n s i n c o s c o s s i n AB A B A B =+，所以443sin cos sin 555B B B =+，故sin 4co tan s B B B ==． 18．【答案】（1）见解析；（2）1．【解析】（1）由已知可得，90BAC ∠=︒，BA AC ⊥．又BA AD ⊥，且AC AD A =，所以AB ⊥平面ACD ．又AB ⊂平面ABC ，所以平面ACD ⊥平面ABC ．（2）由已知可得，3DC CM AB ===，DA =23BP DQ DA ==，所以BP =QE AC ⊥，垂足为E ，则13QE DC ∥．由已知及（1）可得DC ⊥平面ABC ，所以QE ⊥平面ABC ，1QE =．因此，三棱锥Q ABP -的体积为111131332Q ABP ABP V QE S -=⨯⨯=⨯⨯⨯⨯︒=△．19．【答案】（1）见解析；（2）0.48；（3）()347.45m ． 【解析】（1）如下图（2）根据以上数据，该家庭使用节水龙头后50天日用水量小于30.35m 的频率为0.20.110.1 2.60.120.050.48⨯+⨯+⨯+⨯=，因此该家庭使用节水龙头后日用水量小于30.35m 的概率的估计值为0.48． （3）该家庭未使用节水龙头50天日用水量的平均数为()110.0510.1530.2520.3540.4590.55260.6550.4850x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=． 该家庭使用了节水龙头后50天日用水量的平均数为()210.0510.1550.25130.35100.45160.5550.3550x =⨯+⨯+⨯+⨯+⨯+⨯=． 估计使用节水龙头后，一年可节省水()()30.480.3536547.45m -⨯=．20．【答案】（1）2234x y +=；（2）(22330x y x +=≠． 【解析】（1）设椭圆方程为()222210x ya b a b +=>>，由已知2222c a c b a c⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩，得1a b c ⎧=⎪=⎨⎪=⎩， ∴椭圆方程为2213x y +=．①当直线AB 的斜率存在时，设直线AB 为y kx m =+，()11,A x y ，()22,B x y ，代入椭圆方程得()()222136310k x kmx m +++-=．∴122613kmx x k -+=+，()21223113m x x k-⋅=+． ∵OA OB ⊥，∴0OA OB ⋅=，即()()()()221212*********x x y y x x kx m kx m k x x km x x m +=+++=++++()()22222316101313m km k km m k k --⎛⎫=+⋅++= ⎪++⎝⎭，即224330m k --=． ∵AB与以原点为圆心的圆相切，∴圆半径r =，则222314m r k ==+，∴圆的方程为2234x y +=． ②当直线AB 的斜率存在时，易知AB方程为x =2234x y +=． （2）设(),P x y ，()11,A x y ，()22,B x y ，由3OP OA OB =+得121233x x x y y y =+⎧⎨=+⎩又直线OA ，OB 的斜率积为13-，∴121213y y x x =-，即121230x x y y +=．∵A ，B 在椭圆上，∴221113x y +=，222213xy +=联立得121212122211222233303333x x x y y y x x y y x y x y ⎧=+⎪=+⎪⎪+=⎨⎪+=⎪⎪+=⎩消去1x ，1y ，2x ，2y ，得22330x y +=．当OA 斜率不存在时，即10x =，得11y =±，20y =，2x =此时x =±同理OB斜率不存在时，x =±，∴P点的轨迹方程为(22330x y x +=≠．21．【答案】（1）210x y --=；（2）见解析． 【解析】（1）()()2212exax a x f x +-'-+=，()02f '=．因此曲线()y f x =在点()0,1-处的切线方程是210x y --=．（2）当1a ≥时，()()21e 1e e x xf x x x +-+≥+-+．令()211e xg x x x +≥+-+，则()121e x g x x +≥++'．当1x <-时，()0g x '<，()g x 单调递减；当1x >-时，()0g x '>，()g x 单调递增； 所以()()10g x g ≥-=．因此()e 0f x +≥．22．【答案】（1）()()22314x y -+-=；（2）30,4⎡⎤⎢⎥⎣⎦．【解析】（1）由题意知，曲线1C 的直角坐标方程为22412x y y +-=．设点(),P x y ''，(),Q x y ． 由中点坐标公式得262x x y y'=-⎧⎨'=⎩，代入22412x y y +-=中，得点Q 的轨迹2C 的直角坐标方程为()()22314x y -+-=． （2）直线l 的普通方程为y ax =≤304a ≤≤， 即实数a 的取值范围是30,4⎡⎤⎢⎥⎣⎦．23．【答案】（1）][(),43,-∞-+∞；（2）[]2,0-． 【解析】（1）当3a =时，()213532 212x x f x x x x --≤-⎧⎪=-<<⎨⎪+≥⎩，当3x ≤-时，由()7f x ≥得217x --≥，解得4x ≤-；当32x -<<时，()7f x ≥无解；当2x ≥时，由()7f x ≥得217x +≥，解得3x ≥， 所以()7f x ≥的解集为][(),43,-∞-+∞．（2）()4f x x ≤-等价于42x a x x +≤---当[]0,2x ∈时，42x a x x +≤---等价于22a x a --≤≤-，由条件得20a --≤且22a -≥，即20a -≤≤．故满足条件的a 的取值范围为[]2,0-．。

选择题：本大题共12个小题，每小题5分，共60分•在每小题给出的四个选项中，只有一项是 符合题目要求的.1. 已知集合 A=[x-1 <x<2) B=<x<3)» 贝ij AU B=() A. (-1, 3) B. (-1, 0) C. (0, 2) D. (2, 3)2、 复数错误!未找到引用源。

在复平面上对应的点位于()A.笫一象限B.第二象限C.第三象限D.笫四象限\(兀 3. ------------------------------------ 己知 cos a =—,则 sin 2a 34. 设D, E, F 分别为AABC 的三边BC, CA, AB 的中点，则错误!未找到引用源。

()A.错误!未找到引用源。

B.错误!未找到引用源。

C.错误!未找到引用源。

D.错误!未找到引用源。

5. 已知点P 是抛物线/ =4兀上的一点，F 为抛物线的焦点,若|PF| = 5,则点P 的横坐标为( )A. 1B. 2C. 3D.4 6. 如图，网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图，则该多面体的表面 积为( ) A. 18 + 36^5 B. 54+18舲 C. 90 D. 819. 设函数/(x),g(x)的定义域为H/W 是奇函数，g(x)是偶函数，则下列结论正确的、71 D.4^2~9~) 10. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”，执行该 稈序框图，若输入的a, b 分别为14, 18,则输出的a =()A. 0B. 2C. 4D. 1411.己知M(3,O)是圆X 2+/-8X -2J + 1O =()内一点，则过M 点最长的弦所在的直线方程 是( )A.兀+歹—3 = 0 B ・ x — y — 3 = 0 C ・ 2x —y —6 = 0 D. 2兀+y —6 = 0 12. 设/(x) = |lgx|,若函数g(x) = f(x)-ax 在区间(0,4)上有三个零点，则实数a 的取值 范围是 金］订竽判 c 罗)屮詈)第II 卷(共90分)填空题(每题5分，满分20分，将答案填在答题纸上)JT jr13. 将函数/(x) = sin(x + ^), (0<^<一)的周期缩小到原来的一半，再向左平移上个单 2 8 位，所得到的函数图象关于y 轴对称，则©的取值为—14. 己知三棱锥P-ABC 的三条侧棱两两互相垂直，且AB = y/5f BC 二护,AC = 2｝则此 三棱锥的外接球的体积为 _________15. 在△八BC 中，b = 2, cosC=-, Z\ABC 的面积为则 a 二是(4 416.甲、乙、丙三位同学，其屮一位是班长，一位是体育委员，一位是学习委员，已知丙的年龄比学委的大，甲与体委的年龄不同，体委比乙年龄小•据此推断班长是 _________三、解答题(本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤•)17.(本小题12分)已知｛匕｝是公差不为零的等差数列，满足冬=7,且色、偽、坷成等比数列(1)•求数列｛色｝的通项公式18.(本小题12分)如图，三棱柱ABC—AiB.Ci的侧棱Ah丄底面ABC, ZACB = 90° , E是棱CG 的中点,F是AB的中点，AC=BC=1, AA)=2(1)求证：CF//平面ABE；(2)求点C到平面ABE的距离。

2019学年度上学期九月考试高三数学(文科)试题Ⅰ 选择题（共60分）一、选择题:本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、已知集合{}2430A x x x =-+≤,{}13B x N x =∈-<<,则A B ⋂= ( ) A.{}0,1,2 B. {}1,2 C. {}1,2,3 D. {}2,3 2、设复数121,1,z i z ai =+=+若复数21z z 为纯虚数,则实数a 等于 ( ) A.1 B.-1 C.2 D.-2 3、函数21x y a-=+(0a >且1)a ≠的图象必经过点 ( )A.(0,1)B.(1,1)C.(2,0)D.(2,2)4、命题“对任意的32,10x R x x ∈-+≤”的否定是 ( ) A.不存在32,10x R x x ∈-+≤ B.存在32,10x R x x ∈-+≤ C.存在32,10x R x x ∈-+> D.对任意的32,10x R x x ∈-+>5、已知()1,6,2a b a b a ==⋅-=,则向量a 与向量b 的夹角是 ( ) A.3π B. 4π C. 6π D. 2π 6、已知等差数列{}n a 的前n 项和为n S ,若4518a a =-,则8S = ( ) A.18 B.36 C.54 D.727、已知0.34a =， 0.912b -⎛⎫= ⎪⎝⎭， 62log 2c = 则,,a b c 的大小关系是 （ ）A. a < b <cB.c a b <<C.c b a <<D.b c a << 8、已知21)4tan(=-πα，则ααααcos sin cos sin -+的值为 （ ） A21B 2C -2D 22 9、 已知函数3()31f x x x =--,在区间[]3,2-上最大值为M ，最小值为N ，则M-N=（ ） A. 20 B. 18 C. 3 D. 0 10、 曲线上的点到直线的最短距离是 （ ）A. B. 2 C. D. 111、在ABC ∆中，内角A 、B 、C 的对边分别为c b a ,,，若ABC ∆的面积为S ，且14,122-+==c b S a ，则ABC ∆外接圆的面积为 （ ） A2πB π2C π3D 42π12、已知函数)1(+=x f y 是定义域为R 的偶函数，且)(x f 在[)∞+，1上单调递减，则不等式)2()12(+>-x f x f 的解集为 ( ) A ． ⎪⎭⎫⎝⎛-1,31 B ．[)3,1 C ．⎪⎭⎫ ⎝⎛-3,31 D ．⎪⎭⎫ ⎝⎛3,31Ⅱ 非选择题（共90分）二、填空题：本大题共4小题，每小题5分，共20 分.请将正确答案填在答题卡的横线上.13、函数()f x =+lg(63)x -的定义域为 ；14、△ABC 内角A ，B ，C 的对边分别为a ，b ，c ，若2cos 2c B a b =+，则C ∠=_________． 15、若,x y 都是正数，且3x y +=，则yx 14+的最小值为__________ 16、设偶函数()f x 在(0,)+∞上为减函数，且(2)0f =，则不等式()()0f x f x x+->的解集为 ；三、解答题：本大题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤. 17、（本题满分12分）已知{}n a 是一个公差小于0的等差数列，且满足362755,16a a a a =+=。

13x的图象是(＜φ＜）的最小正周期为π，将该函数的A.关于点（，0）对称 B.关于直线x=对称2019届高三数学9月月考试题文一、选择题（本题共12道小题，每小题5分，共60分）1.复数z=2-i2+i（i为虚数单位）在复平面内对应的点所在象限为()A．第一象限B．第二象限C．第三象限D．第四象限2.已知集合A={x|x2﹣x﹣6≥0}，B={x|﹣3≤x≤3}，则A∩B等于（）A．[﹣3，﹣2]B．[2，3]C．[﹣3，﹣2]∪{3}D．[2，3]∪{﹣3}3.已知命题p：∀x∈[1,2]，使e x-a≥0.若⌝p是假命题，则实数a的取值范围为（）A.（-∞，e2]B.（-∞，e]C.[e，+∞）D.[e2，+∞）4.下列命题正确的是（）A．命题“若α=β，则sinα=sinβ”的逆否命题为真命题B．命题“若a<b，则ac2≤bc2”的逆命题为真命题C．命题“∀x>0,5x>0”的否定是“∃x≤0,5x0≤0”D．“x<-1”是“ln(x+2)<0”的充分不必要条件15.设a=log3，b=()0.2，c=23，则（）12A．a<b<c B．c<b<a C．c<a<b D．b<a<c6.函数y=x ln x)A B C D7.已知函数f（x）=sin（ωx+φ）（w＞0，-ππ22图象向左平移π6个单位后，得到的图象对应的函数为奇函数，则f（x）的图象是（）π5π1212，0）对称 D.关于直线 x = 对称8.要想得到函数 y = sin 2 x + ⎪ 的图象，只需将 y = sin 2 x + ⎪ 的图像()π ⎫ C.向右平移 个单位D.向右平移 个单位，则 tan - 2θ ⎪ = ( )7D. - ⎛ 3 ⎫3 3 ⎫ 3 0, 3 ⎪ ⎛ 3 ⎫ ) ⋃ 0, ⎪ ,0) ⋃ ,+∞ ⎪⎪ A. (-∞,B ． (- C. D ． 3 ⎪ 3 ⎪ ⎝ ⎝ 3 3 3 ⎝ 3 A ． -5照此规律，第五个不等式为.2 ) 的部分图象如图所示，则C.关于点（5π12π12⎛ ⎛ π ⎫ ⎝ 3 ⎭ ⎝6 ⎭A.向左平移 π6个单位B.向左平移π12个单位π6π129.已知 tan θ =1 ⎛ π ⎫2 ⎝ 4 ⎭A.7B. －7C. 11710.函数 y = 3x 2 - 2 ln x 的单调增区间为（）⎛ ⎛ ⎫ ,+∞ ⎪⎪⎝ ⎭⎭4x + a11. 已知函数 f ( x ) = 是奇函数，则 f (a) 的值为（）2x5 33B ．C ． -D ．222 212. 设函数 f ′(x )是奇函数 f （x ）（x ∈R ）的导数，f （-1）=0，当 x ＞0 时，xf ′(x )-f （x ）＜0，则使得 f （x ）＞0 成立的 x 的取值范围是（）A.（－∞, －1）∪（0,1）B.（－1,0）∪（1，+∞）C.（－∞，－1）∪（－1,0）D.（0,1）∪（1，+∞）二、填空题（本题共 4 道小题，每小题 5 分，共 20 分）13.观察下列不等式1 + 122 <3 21 +1 + 1 1 5 + < ， 22 33 3 1 1 1 5 + + <22 32 42 3……．．．14.若函数 y = A s in(ωx + ϕ)( A > 0,ω > 0, ϕ <该函数解析式是 .π．15.已知函数 f ( x ) = xe x + 2 ，则曲线 y = f ( x ) 在点 (0, f (0)) 处的切线方程为16 关于函数 f （x ）=4sin （2x+ ），（x ∈R ）有下列结论：①y=f（x ）是以 π 为最小正周期的周期函数；②y=f（x ）可改写为 y=4cos （2x ﹣③y=f（x ）的最大值为 4；）；④y=f（x ）的图象关于直线 x=对称；则其中正确结论的序号为．三、解答题（本题共 2 道小题,第 1 题 0 分,第 2 题 0 分,共 0 分）17 已知函数 f ( x ) =3 sin 2 x - 2cos 2 x - 1, x ∈ R .(Ⅰ) 求函数 f ( x) 的最小正周期和最小值；(Ⅱ) 在 ∆ABC 中, A, B, C 的对边分别为 a, b , c ,若 c =求 a, b 的值.3, f (C ) = 0,sin B = 2sin A ，18.已知△ABC 的内角 A , B , C 的对边分别为 a , b , c ,且 2c ⋅ cos B - b = 2a .（Ⅰ）求角 C 的大小；（Ⅱ）设角 A 的平分线交 BC 于 D ，且 AD = 3 ，若 b = 2 ，求△ABC 的面积 .1 9.如图，在半径为 30cm 的半圆形铁皮上截取一块矩形材料 A （点 A ，B 在直径上，点 C ，D在半圆周上），并将其卷成一个以 AD 为母线的圆柱体罐子的侧面（不计剪裁和拼接损耗）（1）若要求圆柱体罐子的侧面积最 大，应如何截取？（2）若要求圆柱体罐子的体积最大，应如何截取？20.已知函数 f (x )= 23ax 3 + x 2 + x - 1.[e 在直角坐标系 xOy 中,曲线 C 的参数方程为 ⎨ ⎪ y =sin α 2坐标方程为 ρcos θ + ⎪ = -2 2 .（ I ）当 a = -的取值范围.12 时，求 f (x )的单调区间； （Ⅱ）若函数 f (x )在 1,3]上单调递增，试求出 a21.已知函数 f （x ）= kx 2 x（k ＞0）．（1）求函数 f （x ）的单调区间；（2）当 k=1 时，若存在 x ＞0，使 lnf （x ）＞ax 成立，求实数 a 的取值范围．（二）选考题：共 10 分。