北京各区2013一模试卷分类汇总之选择第8题

通州区初三年级模拟考试数学试卷2013年5月考生须知 1．本试卷共6页，共五道大题，25道小题，满分120分.考试时间120分钟. 2．在试卷和答题卡上准确填写学校名称和姓名.3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效.4．考试结束，将本试卷、答题卡和草稿纸一并交回. 一、选择题（本题共32分，每小题4分）在每道小题给出的四个备选答案中，只有一个是符合题目要求的，请将所选答案前的字母按规定要求填涂在答题纸第1－8题的相应位置上． 1．3-的倒数是A ．3B ．3-C ．13-D ．132．在下列几何体中，主视图、左视图和俯视图形状都相同的是A B C D3．2012年，北京实现地区生产总值约17800亿元，比2011年增长百分之七点多.将17800用科学记数法表示应为 A ．17.8×103B ．1.78×105C ．0.178×105D ．1.78×1044．如图，A 、B 、C 是⊙O 上的三个点，∠ABC =32°， 则∠AOC 的度数是 A ．32°B ．64°C ．16°D ．58°5．端午节吃粽子是中华民族的传统习俗.妈妈买了2只红豆粽和3只咸肉粽，粽子除内部馅料不同外其它均相同．小颖任意吃一个，吃到红豆粽的概率是 A ．25 B ．12C ．15D ．236. 一个扇形的圆心角为90°，半径为2，则这个扇形的面积是 A ．6πB ．4πC ．2πD ．π7．某班开展以“提倡勤俭节约，反对铺张浪费”为主题教育活动. 为了解学生每天使用零花钱的情况，小明随机调查了10名同学，结果如下表：每天使用零花钱（单位：元）2 3 45 人数12412O BAC关于这10名同学每天使用的零花钱，下列说法正确的是 A ．平均数是2.5 B ．中位数是3C ．众数是2D ．方差是48． 如图，在直角坐标系xoy 中，已知()01A ，，()0B 3，，以线段AB 为边向上作菱形ABCD ，且点D 在y 轴上.若菱形ABCD 以每秒2个单位长度的速度沿射线AB 滑行，直至顶点D 落在x 轴上时停止．设菱形落在x 轴下方部分的面积为S ，则表示S 与滑行时间的函数关系的图象为第8题图（1） 第8题图（2）二、填空题（本题共16分，每小题4分） 9．若分式2x x-的值为零，则x = ． 10．分解因式：322x x x -+= ． 11．如图，AB ∥CD ，点E 在AB 上，且DC DE =，70AEC ∠=︒，则D ∠的度数是______.12．定义一种对正整数n 的“F 运算”：①当n 为奇数时，结果为31n +；②当n 为偶数时，结果为kn 2（其中k 是使得kn 2为奇数的正整数），并且运算重复进行.例如，取6n =，则：12363105F F F −−−→−−−→−−−→① ②②第次第次第次……，若1n =，则第2次“F 运算”的结果是 ；若13n =，则第2013次“F 运算”的结果是 .第11题图CDA E BSSSDCBAtO 1234213tO1234213tO12342133124321OtS yxOABCD第8题图（2）第8题图（1）D CBA Oxy三、解答题（本题共30分，每小题5分） 13．计算：()123tan 302312--+-+o．14．解不等式组20512(1)x x x -<⎧⎨+>-⎩，．15. 已知：如图，AB ＝AC ，点D 、E 分别在AB 、AC 上，且使AE ＝AD .求证：∠B ＝∠C .16．化简求值：2221y x y x y x⎛⎫-+ ⎪-⎝⎭g ，其中30x y -=，且0y ≠.ECA D B17．已知(42)A -，，(24)B -，是一次函数y kx b =+的图象和反比例函数my x=图象的两个交点．（1）求反比例函数和一次函数的表达式；（2）将一次函数y kx b =+的图象沿y 轴向上平移n 个单位长度，交y 轴于点C ，若12ABC S =V ，求n 的值.18. 列方程或列方程组解应用题：根据城市发展规划设计，某市工程队为该城市修建一条长4800米的公路.铺设600米后，为了缩短工期，该工程队增加了人力和设备，实际每天修建公路的长度是原计划的2倍，结果共用9天完成任务.问原计划每天修建公路多少米?四、解答题（本题共20分，每小题5分）19．某中学组织全校1000名学生参加了有关“低碳环保”知识竞赛．为了解本次知识竞赛的成绩分布情况，从中随机抽取了部分学生的成绩（得分取正整数，满分为100分），并绘制了如图的频数分布表和频数分布直方图（不完整）．请根据以上提供的信息，解答下列问题： （1）直接写出频数分布表中a ，b 的值，补全频数分布直方图；（2）学校将对成绩在90分以上（不含90分）的学生进行奖励，请估计全校1000名学生中约有多少名获奖？20．如图，在矩形ABCD 中，AB =3，BC ＝3，△DCE 是等边三角形，DE 交AB 于点F ，求△BEF 的周长．分组／分 频数 频率 50<x ≤60 10 a 60<x ≤70 b 70<x ≤80 0.2 80<x ≤90 52 0.26 90<x ≤100 0.37 合计1频数 80 70 60 50 40 30 20 10 0成绩/分50 60 70 80 90 100A DFEB C21．已知：如图，AB 是⊙O 的直径，AC 是弦．过点A 作∠BAC 的角平分线，交⊙O 于点D ，过点D 作AC 的垂线，交AC 的延长线于点E ． （1）求证：直线ED 是⊙O 的切线；（2）连接EO ，交AD 于点F ，若5AC =3AB ，求EOFO的值．22. 如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形ABCD 的边长为2，E 是AD 的中点，沿CE 将菱形ABCD 剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．（1）在下面的菱形斜网格中画出示意图；（2）若所拼成的直角三角形、等腰梯形、矩形的面积分别记为S 1、S 2、S 3，周长分别记为l 1、l 2、3l ，判断所拼成的三种图形的面积、周长的大小关系（用“=”、“＞”、“＜”、“）：面积关系是 ； 周长关系是 ．第22题图（矩形）（等腰梯形）（直角三角形）E DCBA ②①EA BCDO第22题图五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23. 已知二次函数()2214y x k x k =-++的图象与x 轴分别交于点()1,0A x 、()2,0B x ，且32-<1x <12-． （1）求k 的取值范围；（2）设二次函数()2214y x k x k =-++的图象与y 轴交于点M ，若OM OB =，求二次函数的表达式；（3）在(2)的条件下，若点N 是x 轴上的一点，以N 、A 、M 为顶点作平行四边形，该平行四边形的第四个顶点F 在二次函数()2214y x k x k =-++的图象上，请直接写出满足上述条件的平行四边形的面积.BD=，以AB为一边作等边三角形ABC.使C、D两点落在直线AB 24．已知：2AD=，4的两侧.（1）如图，当∠ADB=60°时，求AB及CD的长；（2）当∠ADB变化，且其它条件不变时，求CD 的最大值，及相应∠ADB的大小.CAD B25．我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点（半圆与二次函数图象的连接点除外），那么这条直线叫做“蛋圆”的切线.如图，二次函数223y x x =--的图象与x 轴交于点A 、B ，与y 轴交于点D ，AB 为半圆直径，半圆圆心为点M ,半圆与y 轴的正半轴交于点C . （1）求经过点C 的“蛋圆”的切线的表达式； （2）求经过点D 的“蛋圆”的切线的表达式；（3）已知点E 是“蛋圆”上一点（不与点A 、点B 重合），点E 关于x 轴的对称点是F ，若点F 也在“蛋圆”上，求点E 的坐标.yCM A O B x D第25题图参考答案及评分标准2013．5 一、选择题：1．C 2．C 3．D 4．B 5．A 6．D 7．B 8．A 二、填空题：9. 2x =； 10. ()21x x -； 11. 40 ； 12. 1，4；三、解答题： 13. 解：原式= 13312323-⨯++， ……………… 4分；= 131232-++， =332+ . ……………… 5分. 14. ()205121x x x -<⎧⎨+>-⎩， ．①②解：解不等式①，得 2x <， ……………… 1分；解不等式②，5122x x +>-， ……………… 2分； 5221x x ->--， ……………… 3分；33x >-，1x >-， ……………… 4分；∴这个不等式组的解集是12x -<< . (5)分.15. 证明：在△ABE 和△AC D 中∵ .AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩，， ……………… 3分；∴△ABE ≌△ACD （SAS ）. ……………… 4分；∴B C ∠=∠. ……………… 5分.第15题图EDC BA16． 解：原式=x yx y x y y x y x -∙⎪⎪⎭⎫ ⎝⎛-+--2222222，x yx y x x -∙-=222， ……………… 1分； xyx y x y x x -∙-+=))((2， ……………… 2分；=xx y+. ……………… 3分； 由30x y -=，得3x y =， ……………… 4分； ∴原式=33y y y +=34y y =34. ……………… 5分.17. 解：(1) 把(42)A -，，(24)B -，分别代入y kx b =+和my x=中， ∴42244.2-=k b k b m ⎧⎪-+=⎪+=-⎨⎪⎪⎩，， ……………… 1分；解得：128.k b m =-⎧⎪=-⎨⎪=-⎩，， ……………… 2分；∴反比例函数的表达式为8y x=-，一次函数的表达式为2y x =-- ； （2）设一次函数2y x =--的图象与y 轴的交点为D ,则()0D ，-2，……………… 3分； ∵12=∆ABC S ， ∴12221421=∙∙+-∙∙CD CD ，……………… 4分； ∴4CD =，∴4n =. ……………… 5分. 18. 解法一:解：设原计划每天修建公路x 米, 则实际每天修建公路2x 米， …… 1分；根据题意得：600480060092x x-+=， ……………… 3分；∴27009x=， ∴300x =.经检验：x =300是原方程的解，且符合实际问题的意义. ……………… 4分； 答： 原计划每天修建公路300米. ……………… 5分. 解法二：解：设铺设600米用x 天, 则增加人力和设备后，用()9x -天完成任务.……………… 1分； 根据题意得：600480060029x x-⨯=-， ……………… 3分； 解得：2x =.经检验：2x =是原方程的解，且符合实际问题的意义. ……………… 4分； ∴6003002=， 答：原计划每天修建公路300米. ……………… 5分. 四、解答题19. （1）0.05a =，24b =. ……………… 2分； 补全频数分布直方图正确； ……………… 4分； （2）0.371000370⨯=. ……………… 5分. 估计全校1000名学生中约有370名获奖. 20．解法一：∵矩形ABCD ，△DCE 是等边三角形，∴30ADF ECB ∠=∠=o ，3ED EC ==， 在Rt △ADF 中，90A ∠=o ，3AD =，∴tan AFADF AD∠=， tan 33033AF ==o， ∴1AF =，∴312FB AB AF =-=-=，2FD =， ……………… 1分；G 第20题图A BCDEF∴321EF ED DF =-=-=， ……………… 2分； 过点E 作EG CB ⊥，交CB 的延长线于点G . ……………… 3分； 在Rt △ECG 中，90EGC ∠=o ，3EC =，30ECG ∠=o ， ∴1322EG EC ==，cos GCECG EC∠=， cos 33032GC ==o ， ∴332GC =， ∴3133322GB GC BC =-=-=， 由勾股定理得，222EB EG GB =+，∴3EB =（舍去负值） ……………… 4分； ∴△BEF 的周长=33EF FB EB ++=+. ……………… 5分. 解法二：∵矩形ABCD ，△DCE 是等边三角形，∴60EDC ECD ∠=∠=o ，3ED EC ==，过点E 作EH CD ⊥交CD 于点H ，交AB 于点G . ……………… 1分； ∴点H 是DC 的中点，点G 是AB 的中点， 30FEG ∠=o ，3GH AD ==，在Rt △EHD 中，90EHD ∠=o ，3ED =， ∴sin EH EDH ED∠=， sin 36032EH ==o ， ∴332EH =， ∴3133322EG EH GH =-=-=. 在Rt △EGF 中，90EGF ∠=o ，60EFG ∠=o ， ∴sin EGEFG EF∠=， H F E D CBA第20题图Gsin 1332602EF ==o， ∴1EF =， ……………… 2分； ∴1122FG EF ==， ∵点G 是AB 的中点，3AB =，∴1322GB AB ==， ∴13222FB FG GB =+=+=， ……………… 3分；由勾股定理得，222EB EG GB =+，∴3EB =（舍去负值） ……………… 4分； ∴△BEF 的周长=33EF FB EB ++=+. ……………… 5分. 解法三：∵矩形ABCD ，△DCE 是等边三角形，∴30ADF ECB ∠=∠=o ，3ED EC ==， 在Rt △ADF 中，90A ∠=o ，3AD =，∴tan AFADF AD∠=， tan 33033AF ==o， ∴1AF =，∴312FB AB AF =-=-=，2FD =， ……………… 1分； ∴321EF ED DF =-=-=， ……………… 2分； 过点B 作BG CE ⊥，交CE 于点G . ……………… 3分； 在Rt △BCG 中，90BGC ∠=o ，3BC =，30ECB ∠=o ，∴1322BG BC ==，cos GCBCG BC∠=，cos 33023GC ==o， ∴32GC =， G 第20题图ABCDEF∴33322GE EC GC =-=-=， 由勾股定理得，222EB EG GB =+，或BG 是线段EC 的垂直平分线，∴3EB =（舍去负值）或BE =BC ， ………… 4分； ∴△BEF 的周长=33EF FB EB ++=+. ………………5分.21． (1)证明：连接OD.∵OD OA =，∴OAD ODA ∠=∠，∵AD 平分BAC ∠，∴BAD CAD ∠=∠，∴ODA CAD ∠=∠， ……………… 1分； ∴AE ∥OD ， ∵DE AE ⊥， ∴ED DO ⊥，∵点D 在⊙O 上，∴ED 是⊙O 的切线； ……………… 2分；（2）解法一：连接CB ,过点O 作OG AC ⊥于点G .…………… 3分； ∵ AB 是⊙O 的直径， ∴90ACB ∠=o ， ∵OG AC ⊥， ∴OG ∥CB ， ∴AG ACAO AB=， ∵5AC =3AB ，∴35AG AO =， ……………… 4分； 设35AG x AO x ==，， ∵DE AE ⊥，ED DO ⊥， ∴四边形EGOD 是矩形， ∴EG OD =，AE ∥OD ，∴5DO x =，5GE x =，8AE x =,第21题图OED C BAG 第21题图OF ED C BA∴△AEF ∽△DFO ，∴EF AEFO OD =， ∴85EF FO = ，∴135EO FO =. ……………… 5分．解法二：连接CB ,过点A 作AH DO ⊥交DO 的延长线于点H . ………… 3分； ∵DE AE ⊥，ED DO ⊥， ∴四边形AHDE 是矩形， ∴EA DH =，AE ∥HD ，AH ∥ED ，∴CAB AOH ∠=∠， ∵ AB 是⊙O 的直径， ∴90ACB ∠=o ， ∴ACB AHO ∠=∠， ∴△AHO ∽△BCA ， ∴OH ACAO AB=， ∵5AC =3AB ，∴35OH AO =， ……………… 4分；设35OH x AO x ==，， ∴5DO x =，8AE DH x ==, ∵AE ∥HD ，∴△AEF ∽△DFO ，∴EF AEFO OD =， ∴85EF FO = ，∴135EO FO =. ……………… 5分．解法三：连接CB ,分别延长AB 、ED 交于点G . ………… 3分； ∵DE AE ⊥，ED DO ⊥， ∴AE ∥OD ，90ODG ∠=o ，HABC D EFO第21题图∴CAB DOG ∠=∠， ∵ AB 是⊙O 的直径， ∴90ACB ∠=o ， ∴ACB ODG ∠=∠， ∴△GDO ∽△BCA ， ∴OD ACOG AB=， ∵5AC =3AB ，∴35OD OG =， ……………… 4分； 设35OD x OG x ==，，∴5AO x =，8AG AO OG x =+=, ∵AE ∥OD ，∴△AEG ∽△ODG ，△AEF ∽△DFO ，∴ AG AE OG OD = ， EF AEFO OD =， ∴85EF FO = ，∴135EO FO =. ……………… 5分.22.(1)画图正确； 每图各1分，共3分；(2)面积关系是 S 1=S 2=S 3 ； ……………… 4分； 周长关系是 l 1>l 2>3l ． ……………… 5分. 五、解答题： 23.解：(1)令0y =，则()22140x k x k -++=解方程得：2x k =或2x =， ……………… 1分；②①②①②①（直角三角形）①②（等腰梯形）（矩形）第21题图F ABD EC GO由题意得：()20A k ，，()20B ，， ∴ 31222-k <<-， ∴3144k -<<-. ……………… 2分；(2)令0x =，则4y k =，∴()04M k ，， ∵OM OB =，∴ 42k -=， ……………… 3分； ∴ 12k =-， ∴22y x x =--. …………… 4分；或∵OM OB =，()20B ，， ∴()0M ，-2，把点M 的坐标分别代入()2214y x k x k =-++中，∴42k =-， ……………… 3分； ∴ 12k =-， ∴22y x x =--. …………… 4分； (3)2，517+，517-. （每个答案各1分） ……………… 7分． 24．解：（1）过点A 作AG BC ⊥于点G . ∵∠ADB=60°，2AD =， ∴1DG =，3AG =，∴ 3GB =，∴ tan 33AG ABG BG ∠==， ∴30ABG ∠=o ，23AB =， ……………… 1分； ∵ △ABC 是等边三角形，∴ 90DBC ∠=o ，23BC =， ……………… 2分；G第24题图D CBA由勾股定理得：()222242327CD DB BC =+=+=. …… 3分；（2）作60EAD ∠=o ，且使AE AD =，连接ED 、EB . ………… 4分； ∴△AED 是等边三角形， ∴AE AD =，60EAD ∠=o ，∵ △ABC 是等边三角形， ∴AB AC =，60BAC ∠=o ，∴EAD DAB BAC DAB ∠+∠=∠+∠， 即EAB DAC ∠=∠，∴△EAB ≌△DAC . ……………… 5分； ∴EB =DC .当点E 、D 、B 在同一直线上时，EB 最大，∴246EB =+=， ……………… 6分； ∴ CD 的最大值为6，此时120ADB ∠=o . …………… 7分.另解：作60DBF ∠=o ，且使BF BD =，连接DF 、AF . 参照上面解法给分. 25．解：（1）由题意得：()10A -，，()30B ，，()03-D ，，()10M ，. ∴2AM BM CM ===， ∴223OC CM OM =-=，∴()0C ，3∵GC 是⊙M 的切线， ∴90GCM ∠=o∴cos OM MCOMC MC MG∠==， ……………… 1分； ∴122MG=， ∴4MG =，∴()30G -，， ∴直线GC 的表达式为333y x =+. ……………… 2分； （2）设过点D 的直线表达式为3y kx =-，第24题图ED CBA FA BCD第24题图G 第25题图y xMO DC B A∴2323,y kx y x x =-⎧⎨=--⎩，∴()220x k x -+=，或1202x x k ==+，0)]2([2=+-=∆k ，或12x x =， …………… 3分；∴2k =-，∴ 过点D 的“蛋圆”的切线的表达式为23y x =--. …………… 4分；（3）假设点E 在x 轴上方的“蛋圆”上，设()E m n ，，则点F 的坐标为()m n -，. EF 与x 轴交于点H ，连接EM . ∴222HM EH EM +=，∴()2214m n -+=，……① ………… 5分； ∵点F 在二次函数223y x x =--的图象上， ∴223m m n --=-，……② 解由①②组成的方程组得：131m n ⎧=+⎪⎨=⎪⎩；131m n ⎧=-⎪⎨=⎪⎩.(0n =舍去)……………… 6分；由对称性可得：131m n ⎧=+⎪⎨=-⎪⎩；131m n ⎧=-⎪⎨=-⎪⎩. ……………… 7分；∴()1131E +，，()2131E -，，()3131E +，-，()4131E -，-.…………… 8分.H F EA B CDO M xy 第25题图。

北京市通州区2013年中考数学一模试卷一、选择题（本题共32分，每小题4分）在每道小题给出的四个备选答案中，只有一个是符合题目要求的，请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上．（﹣）的倒数是﹣2．（4分）（2013•通州区一模）在下列几何体中，主视图、左视图和俯视图形状都相同的可B2011年3．（4分）（2013•通州区一模）2012年，北京实现地区生产总值约17800亿元，比4．（4分）（2013•通州区一模）如图，A、B、C是⊙O上的三个点，∠ABC=32°，则∠AOC 的度数是（）5．（4分）（2013•通州区一模）端午节吃粽子是中华民族的传统习俗，妈妈买了2只红豆粽、3只碱水粽、5只干肉粽，粽子除内部馅料不同外其它均相同，小颖随意吃一个，吃到红豆B=6．（4分）（2013•通州区一模）一个扇形的圆心角为90°，半径为2，则这个扇形的面积是=7．（4分）（2013•通州区一模）某班开展以“提倡勤俭节约，反对铺张浪费”为主题教育活动．为[，则方差[））﹣8．（4分）（2013•通州区一模）如图，在直角坐标系xoy中，已知A（0，1），B（，0），以线段AB为边向上作菱形ABCD，且点D在y轴上．若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行，直至顶点D落在x轴上时停止．设菱形落在x轴下方部分的面积为S，则表示S与滑行时间t的函数关系的图象为（）．．．D．=2BAO==，×=轴方向滑落的速度，S=t=S=×=×﹣（•=2﹣二、填空题（本题共16分，每小题4分）9．（4分）（2013•通州区一模）若分式的值为零，则x=2．时，分式10．（4分）（2013•通州区一模）分解因式：x3﹣2x2+x=x（x﹣1）2．11．（4分）（2013•通州区一模）如图，AB∥CD，点E在AB上，且DC=DE，∠AEC=70°，则∠D的度数是40°．12．（4分）（2013•通州区一模）定义一种对正整数n的“F运算”：①当n为奇数时，结果为3n+1；②当n为偶数时，结果为（其中k是使得为奇数的正整数），并且运算重复进行．例如，取n=6，则：631056 …，若n=1，则第2次“F运算”的结果是1；若n=13，则第2013次“F运算”的结果是4．=1=5=1三、解答题（本题共30分，每小题5分）13．（5分）（2013•通州区一模）计算：．+1+214．（5分）（2013•通州区一模）解不等式组：15．（5分）（2013•通州区一模）已知：如图，AB=AC，AE=AD，点D、E分别在AB、AC 上．求证：∠B=∠C．16．（5分）（2013•通州区一模）化简求值：，其中x﹣3y=0，且y≠0．．==．17．（5分）（2013•通州区一模）已知A（﹣4，2），B（2，﹣4）是一次函数y=kx+b的图象和反比例函数图象的两个交点．（1）求反比例函数和一次函数的表达式；（2）将一次函数y=kx+b的图象沿y轴向上平移n个单位长度，交y轴于点C，若S△ABC=12，求n的值．和2=，一次函数的表达式为18．（5分）（2013•通州区一模）列方程或方程组解应用题：根据城市规划设计，某市工程队准备为该城市修建一条长4800米的公路．铺设600m后，为了尽量减少施工对城市交通造成的影响，该工程队增加人力，实际每天修建公路的长度是原计划的2倍，结果9天完成任务，该工程队原计划每天铺设公路多少米？四、解答题（本题共20分，每小题5分）19．（5分）（2013•通州区一模）某中学组织全校1000名学生参加了有关“低碳环保”知识竞赛．为了解本次知识竞赛的成绩分布情况，从中随机抽取了部分学生的成绩，并绘制了如图（1）直接写出频数分布表中a，b 的值，补全频数分布直方图；（2）学校将对成绩在90分以上（不含90分）的学生进行奖励，请估计全校1000名学生中约有多少名获奖？0.0520．（5分）（2013•通州区一模）如图，在矩形ABCD中，AB=3，BC=，△DCE是等边三角形，DE交AB于点F，求△BEF的周长．AD=ADF==，EC=ECG=，BC==EB==EF+FB+EB=3+．GH=AD= EDH==，GH==，=EF=，AB=，EB==EF+FB+EB=3+．AD=ADF==，BC=BCG=，，﹣=EB==EF+FB+EB=3+．21．（5分）（2013•通州区一模）已知：如图，AB是⊙O的直径，AC是弦．过点A作∠BAC 的角平分线，交⊙O于点D，过点D作AC的垂线，交AC的延长线于点E．（1）求证：直线ED是⊙O的切线；（2）连接EO，交AD于点F，若5AC=3AB，求的值．得出求出，求出22．（5分）（2013•通州区一模）如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形ABCD的边长为2，E是AD的中点，按CE将菱形ABCD 剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．（1）在下面的菱形斜网格中画出示意图；（2）判断所拼成的三种图形的面积（s）、周长（l）的大小关系（用“=”、“＞”或“＜”连接）：面积关系是；周长关系是．=222=2=6+2；，面积=2五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．（7分）（2013•通州区一模）已知二次函数y=x2﹣2（k+1）x+4k的图象与x轴分别交于点A（x1，0）、B（x2，0），且＜x1＜．（1）求k的取值范围；（2）设二次函数y=x2﹣2（k+1）x+4k的图象与y轴交于点M，若OM=OB，求二次函数的表达式；（3）在（2）的条件下，若点N是x轴上的一点，以N、A、M为顶点作平行四边形，该平行四边形的第四个顶点F在二次函数y=x2﹣2（k+1）x+4k的图象上，请直接写出满足上述条件的平行四边形的面积．的不等式由题意得，故可得：，，则，或，×+2=5+×+2=5；或24．（7分）（2013•通州区一模）已知：，PB=4，以AB为一边作正方形ABCD，使P、D两点落在直线AB的两侧．（1）如图，当∠APB=45°时，求AB及PD的长；（2）当∠APB变化，且其它条件不变时，求PD的最大值，及相应∠APB的大小．，AE=PE=×=1=．B===AG==，，．，PD====25．（8分）（2013•通州区一模）我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点（半圆与二次函数图象的连接点除外），那么这条直线叫做“蛋圆”的切线．如图，二次函数y=x2﹣2x﹣3的图象与x轴交于点A、B，与y轴交于点D，AB为半圆直径，半圆圆心为点M，半圆与y轴的正半轴交于点C．（1）求经过点C的“蛋圆”的切线的表达式；（2）求经过点D的“蛋圆”的切线的表达式；（3）已知点E是“蛋圆”上一点（不与点A、点B重合），点E关于x轴的对称点是F，若点F也在“蛋圆”上，求点E的坐标．cos解由①②组成的方程组得：；；，，。

北京市西城区2013年高三一模试卷 高三数学（理科）参考答案及评分标准 2013.4一、选择题：本大题共8小题，每小题5分，共40分.1． B ； 2．A ； 3．D ； 4．B ； 5．C ； 6．B ； 7．D ； 8．A ．二、填空题：本大题共6小题，每小题5分，共30分.9．22230x y y +--=； 10．5； 11．32-12．152，5； 13．1 14．1，．注：12、14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分. 15．（本小题满分13分）（Ⅰ）解：依题意，得π()04f =， ………………1分即ππsincos 044a -==， (3)分解得 1a =． ………………5分（Ⅱ）解：由（Ⅰ）得 ()sin cos f x x x =-． ………………6分()()()cos g x f x f x x x =⋅-+(sin cos )(sin cos )2x x x x x =---+ ………………7分22(cos sin )2x x x =- ………………8分cos 22x x =+ ………………9分π2sin(2)6x =+． ………………10分由πππ2π22π262k x k -≤+≤+，得 ππππ36k x k -≤≤+，k ∈Z ． (12)分所以 ()g x 的单调递增区间为ππ[π,π]36k k -+，k ∈Z ． ………………13分16．（本小题满分13分）（Ⅰ）解：依题意，甲、乙两组的学生人数之比为 (35):(22)2:1++=， ……………1分所以，从甲组抽取的学生人数为2323⨯=；从乙组抽取的学生人数为1313⨯=．………2分设“从甲组抽取的同学中恰有1名女同学”为事件A ， ………………3分则113528C C 15()C 28P A ⋅==， 故从甲组抽取的同学中恰有1名女同学的概率为1528． (5)分 （Ⅱ）解：随机变量X的所有取值为0,1,2,3． ………………6分21522184C C 5(0)C C 28P X ⋅===⋅， 111213525221218484C C C C C 25(1)C C C C 56P X ⋅⋅⋅==+=⋅⋅， 211113235221218484C C C C C 9(2)C C C C 28P X ⋅⋅⋅==+=⋅⋅， 21322184C C 3(3)C C 56P X ⋅===⋅．……………10分所以，随机变量X 的分布列为:………………11分5259350123285628564EX =⨯+⨯+⨯+⨯=． (13)分17．（本小题满分14分）（Ⅰ）证明：因为BC AB 2=，60ABC ︒∠=，在△ABC 中，由余弦定理可得 BC AC 3=，所以 BC AC ⊥． ………………2分 又因为 AC FB ⊥，所以⊥AC 平面FBC ． ………………4分 （Ⅱ）解：因为⊥AC 平面FBC ，所以FC AC ⊥．因为FC CD ⊥，所以⊥FC 平面ABCD ．………………5分 所以,,CA CF CB 两两互相垂直，如图建立的空间直角坐标系xyz C -． ………………6分在等腰梯形ABCD 中，可得 CB CD =．设1BC =，所以11(0,0,0),(0,1,0),,0),,1)22C A B D E --．所以)1,21,23(-=CE ，)0,0,3(=CA ，)0,1,0(=CB ．设平面EAC 的法向量为=()x,y,z n ，则有0,0.CE CA ⎧⋅=⎪⎨⋅=⎪⎩n n 所以 10,20.x y z -+== 取1z =，得=n (0,2,1)． (8)分设BC 与平面EAC 所成的角为θ，则||sin |cos ,|||||CB CB CB ⋅=〈〉==θn n n 所以 BC 与平面EAC 所成角的正弦值为552． (9)分（Ⅲ）解：线段ED 上不存在点Q ，使平面EAC ⊥平面QBC ．证明如下： ………………10分假设线段ED 上存在点Q ，设),21,23(t Q - )10(≤≤t ，所以),21,23(t CQ -=．设平面QBC 的法向量为=m ),,(c b a ，则有0,0.CB CQ ⎧⋅=⎪⎨⋅=⎪⎩m m 所以 0,10.2b b tc =⎧-+= 取 1=c ，得=m )1,0,32(t -． (12)分要使平面EAC ⊥平面QBC ，只需0=⋅n m ，………………13分即002110⨯+⨯+⨯=， 此方程无解．所以线段ED 上不存在点Q ，使平面EAC ⊥平面QBC ． ………………14分18.（本小题满分13分） （Ⅰ）解：()f x 的定义域为(0,)+∞， ………………1分且11()ax f x a x x -'=-=． ………………2分① 当0a ≤时，()0f x '<，故()f x 在(0,)+∞上单调递减．从而)(x f 没有极大值，也没有极小值． ………………3分② 当0a >时，令()0f x '=，得1x a =．()f x 和()f x '的情况如下：故()f x 的单调减区间为1(0,)a ；单调增区间为1(,)a +∞．从而)(x f 的极小值为1()1ln f aa =+；没有极大值． (5)分（Ⅱ）解：()g x 的定义域为R ，且 ()e 3axg x a '=+． ………………6分③ 当0a >时，显然 ()0g x '>，从而()g x 在R 上单调递增．由（Ⅰ）得，此时()f x 在1(,)a +∞上单调递增，符合题意． ………………8分④ 当0a =时，()g x 在R 上单调递增，()f x 在(0,)+∞上单调递减，不合题意．……9分⑤ 当0a <时，令()0g x '=，得013ln()x a a =-．()g x 和()g x '的情况如下表：当30a -≤<时，00x ≤，此时()g x 在0(,)x +∞上单调递增，由于()f x 在(0,)+∞上单调递减，不合题意． ………………11分当3a <-时，00x >，此时()g x 在0(,)x -∞上单调递减，由于()f x 在(0,)+∞上单调递减，符合题意． 综上，a 的取值范围是(,3)(0,)-∞-+∞． (13)分 19．（本小题满分14分）（Ⅰ）解：依题意，当直线AB 经过椭圆的顶点(0,)b 时，其倾斜角为60︒． ………………1分设 (,0)F c -，则tan 60bc ︒==．2分 将 b =代入 222a b c =+，解得 2a c =． ………………3分所以椭圆的离心率为12c e a ==． ………………4分（Ⅱ）解：由（Ⅰ），椭圆的方程可设为2222143x y c c +=． ………………5分 设11(,)A x y ，22(,)B x y ．依题意，直线AB 不能与,x y 轴垂直，故设直线AB 的方程为()y k x c =+，将其代入2223412x y c +=，整理得222222(43)84120k x ck x k c c +++-=． ………………7分则2122843ck x x k -+=+，121226(2)43cky y k x x c k +=++=+，22243(,)4343ck ck G k k -++． (8)分因为 GD AB ⊥，所以 2223431443Dckk k ck x k +⨯=---+，2243D ck x k -=+． ………………9分因为 △GFD ∽△OED ，所以 2222222212222243()()||434343||()43ck ck ck S GD k k k ck S OD k ---++++==-+ (11)分222242222242(3)(3)99999()ck ck c k c k ck c k k ++===+>． ………………13分所以12S S 的取值范围是(9,)+∞． ………………14分20．（本小题满分13分）（Ⅰ）解：当5n =时，由51(,)||7i i i d A B a b ==-=∑，得5|12||24||12||21||3|7a -+-+-+-+-=，即 5|3|2a -=．由 *5a ∈N ，得 51a =，或55a =． ………………3分 （Ⅱ）（ⅰ）证明：设12(,,,)n A a a a =，12(,,,)n B b b b =，12(,,,)n C c c c =．因为 0∃>λ，使 AB BC λ=，所以 0∃>λ，使得 11221122(,,)((,,)n n n n b a b a b a c b c b c b ---=---λ,,，即 0∃>λ，使得 ()ii i i b a c b λ-=-，其中1,2,,i n =．所以i i b a -与(1,2,,)i i c b i n -=同为非负数或同为负数．………………5分所以11(,)(,)||||nni i i i i i d A B d B C a b b c ==+=-+-∑∑1(||||)ni i i i i b a c b ==-+-∑1||(,)ni i i c a d A C ==-=∑． ………………6分（ⅱ）解：设,,n A B C S ∈，且(,)(,)(,)d A B d B C d A C +=，此时不一定0∃>λ，使得AB BC λ=． ………………7分反例如下：取(1,1,1,,1)A =，(1,2,1,1,,1)B =，(2,2,2,1,1,,1)C ，则 (,)1d A B =，(,)2d B C =，(,)3d A C =，显然(,)(,)(,)d A B d B C d A C +=． 因为(0,1,0,0,,0)AB =，(1,0,1,0,0,,0)BC =，所以不存在>0λ，使得AB BC λ=． ………………8分（Ⅲ）解法一：因为 1(,)||ni i i d A B b a ==-∑，设(1,2,,)i i b a i n -=中有()m m n ≤项为非负数，n m -项为负数．不妨设1,2,,i m=时0i i b a -≥；1,2,,i m m n =++时，0i i b a -<．所以 1(,)||ni i i d A B b a ==-∑12121212[()()][()()]m m m m n m m n b b b a a a a a a b b b ++++=+++-+++++++-+++因为 (,)(,)d I A d I B p ==，所以11(1)(1)n niii i a b ==-=-∑∑， 整理得11n ni ii i a b===∑∑．所以 12121(,)||2[()]ni i m m i d A B b a b b b a a a ==-=+++-+++∑．……………10分因为121212()()m n m m n b b b b b b b b b +++++=+++-+++()()1p n n m p m ≤+--⨯=+； 又121m a a a m m+++≥⨯=，所以1212(,)2[()]m m d A B b b b a a a =+++-+++2[()]2p m m p ≤+-=．即 (,)2d A B p ≤． ……………12分 对于 (1,1,,1,1)A p =+，(1,1,1,,1)B p =+，有 A ，n B S ∈，且(,)(,)d I A d I B p ==，(,)2d A B p =．综上，(,)d A B 的最大值为2p ． ……………13分 解法二：首先证明如下引理：设,x y ∈R ，则有 ||||||x y x y +≤+． 证明：因为 ||||x x x -≤≤，||||y y y -≤≤， 所以 (||||)||||x y x y x y -+≤+≤+，即 ||||||x y x y +≤+．所以11(,)|||(1)(1)|n ni i i i i i d A B b a b a ===-=-+-∑∑1(|1||1|)ni i i b a =≤-+-∑11|1||1|2nni i i i a b p===-+-=∑∑． ……………11分上式等号成立的条件为1i a =，或1i b =，所以 (,)2d A B p ≤． ……………12分 对于 (1,1,,1,1)A p =+，(1,1,1,,1)B p =+，有 A ，n B S ∈，且(,)(,)d I A d I B p ==，(,)2d A B p =．综上，(,)d A B 的最大值为2p ． ……………13分。

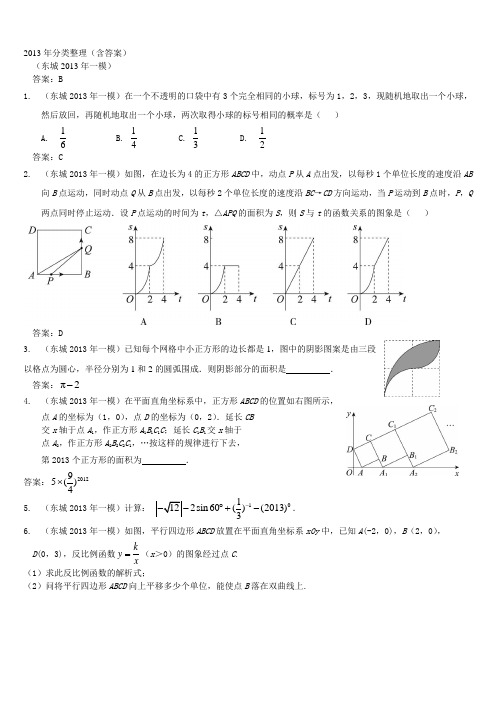
2013年分类整理（含答案） （东城2013年一模） 答案：B1. （东城2013年一模）在一个不透明的口袋中有3个完全相同的小球，标号为1，2，3，现随机地取出一个小球，然后放回，再随机地取出一个小球，两次取得小球的标号相同的概率是（ ） A.16 B. 14 C. 13 D. 12答案：C2. （东城2013年一模）如图，在边长为4的正方形ABCD 中，动点P 从A 点出发，以每秒1个单位长度的速度沿AB向B 点运动，同时动点Q 从B 点出发，以每秒2个单位长度的速度沿BC →CD 方向运动，当P 运动到B 点时，P ，Q 两点同时停止运动．设P 点运动的时间为t ，△APQ 的面积为S ，则S 与t 的函数关系的图象是（ ）答案：D3. （东城2013年一模）已知每个网格中小正方形的边长都是1，图中的阴影图案是由三段 以格点为圆心，半径分别为1和2的圆弧围成．则阴影部分的面积是 ． 答案：π2-4. （东城2013年一模）在平面直角坐标系中，正方形ABCD 的位置如右图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于 点A 2，作正方形A 2B 2C 2C 1，…按这样的规律进行下去， 第2013个正方形的面积为 ． 答案：201295()4⨯5. （东城2013年一模）计算： 1012sin 60()(2013)3--︒+-．6. （东城2013年一模）如图，平行四边形ABCD 放置在平面直角坐标系xOy 中，已知A (-2，0)，B （2，0），D (0，3)，反比例函数ky x=（x ＞0）的图象经过点C . （1）求此反比例函数的解析式；（2）问将平行四边形ABCD 向上平移多少个单位，能使点B 落在双曲线上.解：（1）∵ 平行四边形ABCD ，A (-2，0)，B （2，0），D (0，3)， ∴ 可得点C 的坐标为（4,3）.∴ 反比例函数的解析式为 12y x=. …………………………………3分 （2）将点B 的横坐标2代入反比例函数12y x=中，可得y =6.∴ 将平行四边形ABCD 向上平移6个单位，能使点B 落在双曲线上.………5分7. （东城2013年一模）如图，四边形ABCD 是矩形，点E 在线段CB 的延长线上，连接DE 交AB 于点F ，∠AED =2∠CED ，点G 是DF 的中点．（1）求证：∠CED =∠DAG ；（2）若BE =1，AG =4，求sin AEB ∠的值． 解：（1）证明：∵ 矩形ABCD ，∴ AD ∥BC .∴ ∠CED =∠ADE .又∵点G 是DF 的中点， ∴ AG =DG .∴ ∠DAG =∠ADE .∴ ∠CED =∠DAG . …………………………2分(2) ∵ ∠AED =2∠CED ，∠AGE =2∠DAG ， ∴ ∠AED =∠AGE . ∴ AE =AG . ∵ AG =4， ∴ AE =4.在Rt △AEB 中，由勾股定理可求AB∴ sin 4AB AEB AE ∠==…………………………5分 8. （东城2013年一模）如图，C 是以AB 为直径的⊙O 上一点，过O 作OE ⊥AC 于点E ，过点A 作⊙O 的切线 交OE的延长线于点F ，连结CF 并延长交BA 的延长线于点P . （1）求证：PC 是⊙O 的切线.（2）若AB =4，AP ∶PC =1∶2，求CF 的长. 解：（1）证明：连结OC ．∵ OE ⊥AC ， ∴ AE =CE ．∴ FA =FC ． ∴ ∠FAC =∠FCA ．∵ OA =OC ， ∴ ∠OAC =∠OCA ．∴ ∠OAC +∠FAC =∠OCA +∠FCA ． 即∠FAO =∠FCO ．∵ FA 与⊙O 相切，且AB 是⊙O 的直径， ∴ FA ⊥AB ． ∴ ∠FCO =∠FAO =90°． ∴ PC 是⊙O 的切线． 2分 （2）∵∠PCO =90°，即∠ACO +∠ACP =90°.又∵∠BCO +∠ACO =90°，∴ ∠ACP =∠BCO .∵ BO =CO ，∴ ∠BCO =∠B .∴ ∠ACP =∠B .∵ ∠P 公共角，∴ △PCA ∽△PBC . ∴PC PA ACPB PC BC ==. ∵ AP ∶PC =1∶2， ∴1=2AC BC . ∵ ∠AEO =∠ACB =90°，∴ OF ∥BC .∴ AOF ABC ∠=∠.∴ 1tan tan 2AOF ABC ∠=∠=. ∴ 1tan 2AF AOF AO ∠==. ∵ AB =4，∴ AO =2 .∴ AF =1 .∴ CF =1 . ………………5分9. （东城2013年一模）在平面直角坐标系xOy 中，抛物线2229y x mx m =-+-与x 轴交于A ，B 两点（点A 在点B 的左侧，且OA ＜OB ），与y 轴的交点坐标为（0，-5）.点M 是线段AB 上的任意一点，过点M （a ，0）作直线MC ⊥x轴，交抛物线于点C ，记点C 关于抛物线对称轴的对称点为D （C ，D 不重合），点P 是线段MC 上一点，连结CD ，BD ，PD .（1）求此抛物线的解析式；（2）当1a =时，问点P 在什么位置时，能使得PD ⊥BD ； （3）若点P 满足14MP MC =，作PE ⊥PD 交x 轴于点E ，问是否存在这样的点E ，使得PE =PD ，若存在，求出点E 的坐标；若不存在，请说明理由.解：（1） 抛物线2229y x mx m =-+-与y 轴交点坐标为（0,-5）， 259m ∴-=-. 解得2m =±.抛物线2229y x mx m =-+-与x 轴交于,A B 两点（点A 在点B 的左侧，且OA OB <）， 2m ∴=.∴抛物线的解析式为245y x x =--. ……….. 2 分（2）过D 点作DF x ⊥轴于点F ，//,CD MF DF MF ⊥ ，CD MF ∴⊥.PD BD ⊥ ,.PDC BDF ∴∠=∠.又=90PCD BFD ∠=∠︒ ，PCD BFD ∴∆∆∽.CD PCFD BF∴=. (1,8),(3,8),(3,0),(5,0)C D F B -- ，设P y （1，）， 28=82y +∴. 解得152y =-.∴当P 的坐标为15(1,)2-时，PD BD ⊥. ……….. 4分 （3）假设E 点存在，MC EM ⊥ ，CD MC ⊥， EMP PCD ∴∠=∠. PE PD ⊥ ，EPM PDC ∴∠=∠. ,PE PD =EPM PDC ∴∆∆≌. ,PM DC EM PD ∴==.设00(,)C x y ，则00(4,)D x y -，001(,)4P x y . 001244x y ∴-=-. 2000124(45)4x x x ∴-=---.解得01x =或03x =.(1,-2)(3,-2)P P ∴或.6PC ∴=.6ME PC ∴==.(7,0)E ∴或(-3,0)E . ………… 8分10. （昌平2013年一模）如图，△ABC 中，∠C =90°，AC =3，点P 是边BC 上的动点，则AP 的长不可能．．．是（ ） A. 2.5 B.3 C.4 D.5答案：A11. （昌平2013年一模）现将背面相同的4张扑克牌背面朝上，洗匀后，从中任意翻开一张是数字5的概率为（ ）A ．14 B ．13 C ．25 D ．12答案：D12. （昌平2013年一模）如图，在Rt △ABC 中，∠ACB =90°，AC =BC =6cm ，动点P 从点A 出发，沿AB方向以每秒的速度向终点B 运动；同时，动点Q 从点B 出发沿BC 方向以每秒1cm 的速度向终点C 运动，将△PQC 沿BC 翻折，点P 的对应点为点P '.设Q 点运动的时间为t 秒，若四边形QP CP '为菱形，则t 的值为（ ）A.B. 2C. D. 3答案：B13. （昌平2013年一模）答案：2314. （昌平2013年一模）如图，在△ABC 中，AB =AC =2，点P 在BC 上．若点P 为BC 的中点，则2m AP BP PC =+⋅的值为 ；若BC 边上有100个不同的点P 1，P 2，…，P 100，且m i =AP i 2+BP i ⋅P i C （i =1,2，…，100），则m =m 1+m 2+…+m 100 的值为 ． 答案：4 , 400（各2分） 15. （昌平2013年一模）将直线y x =沿y 轴向下平移后，得到的直线与x 轴交于点A （30，），与双曲线my x=（0x >）交于点B ．（1）求直线AB 的解析式； （2）设点B 的纵坐标为a ，求m 的值（用含a 的代数式表示）．B P PCB A解：（1）依题意，设直线AB 的解析式为y = x + b ．…………………………………… 1分 ∵直线AB 与x 轴交于点A （3，0）， ∴0 = 3 + b .∴b = -3. ………………………………………………………… 2分 ∴直线AB 的解析式为y = x - 3. ………………………… 3分（2）∵直线AB 与双曲线my x=（x ＞0）交于点B ，且点B 的纵坐标为a ， ∴a = x -3.∴x = a + 3. ………………………………………………………… 4分∴3m a a =+. ∴m = a (a + 3). ………………………………………………… 5分16. （昌平区2013年一模）如图，四边形ABCD 是⊙O 的内接正方形，延长AB 到E ，使BE =AB ，连接CE . （1）求证：直线CE 是⊙O 的切线；（2）连接OE 交BC 于点F ，若OF =2 , 求EF 的长.E（1）证明：连接OC∵四边形ABCD 是O 的内接正方形，∴AB=BC ，CO 平分∠DCB ，∠DCB =∠ABC =90°. ∴∠1=45°，∠EBC =90°. ∵AB=BE ， ∴BC=BE . ∴∠2=45°.∴∠OCE =∠1+∠2 = 90°. ∵点C 在O 上，∴直线CE 是O 的切线. …………………………………… 2分（2）解：过点O 作OM ⊥AB 于M ,∴11=22AM BM AB BE ==.∴23BE ME =. ………………………………………………3分 ∵FB ⊥AE , ∴FB ∥OM .∴△EFB ∽△EOM . …………………………………………………4分 ∴EF EBEO EM =. ∴223EF EF =+. EF = 4. ……………………………………………………5分 17. （昌平区2013年一模）已知抛物线22y x kx k =-+-+． （1）求证：无论k 为任何实数，该抛物线与x 轴都有两个交点； （2）在抛物线上有一点P （m ，n ），n <0，OP =103，且线段OP 与x 轴正半轴所夹锐角的正弦值为45，求该抛物线的解析式；（3）将（2）中的抛物线x 轴上方的部分沿x 轴翻折，与原图象的另一部分组成一个新的图形M ，当直线y x b =-+与图形M 有四个交点时，求b 的取值范围.（1）证明：当y =0时，得220x kx k -+-=.∵22244(2)(2)4b ac k k k -=--=-+. ∵2(2)0k -≥， ∴2(2)40k -+>.∴无论k 为任何实数，该抛物线与x 轴都有两个交点. ……………… 3分（2）解：如图，过点P 作P A ⊥x 轴于A ,则∠OAP =90°，依题意得：104,sin 35OP POA =∠=.∴8,23AP OA ==.∵n <0,∴8(2,)3P -.∵P 在抛物线上， ∴84223k k -=-+-+. ∴23k =-.∴抛物线解析式为22833y x x =--+. ………………………………5分 （3）当y =0时，228033x x +-=. ∴1242,3x x =-=，∴抛物线与x 轴相交于点4(2,0),(,0)3.B C -当直线y = - x + b 经过点C （-2，0）时，b = -2. …………………………6分 当直线y = - x + b 与抛物线228+-33y x x =相切时，22833x +x-x b =-+，∴△ =2584()093b ++=. ∴ b = 12136-. ……………………………………………………7分∴ 当12136-＜b ＜-2时，直线与图形M 有四个交点. …………………………8分18. （昌平区2013年一模）已知：如图，在□ABCD 中，∠BAD ，∠ADC 的平分线AE ，DF 分别与线段BC 相交于点E ，F ，AE 与DF 相交于点G ． （1）求证：AE ⊥DF ；（2）若AD =10，AB =6，AE =4，求DF 的长．GA EBCDF(1)证明：∵四边形ABCD 是平行四边形， ∴AB ∥DC .∴∠BAD +∠ADC=180°. ………………………………………1分 ∵AE 、DF 分别平分∠BAD 、∠ADC ，∴111,222BAD ADC ∠=∠∠=∠ . 4321GA EBCDF∴112()902BAD ADC ∠+∠=∠+∠=︒ .∴∠AGD=90°.∴AE ⊥DF . ………………………………………………………2分(2)由（1）知：AD ∥BC ,且BC= AD = 10，DC =AB =6，∠1=∠3,∠2=∠4 . ∴∠1=∠AEB ,∠2=∠DFC . ∴∠3=∠AEB ,∠4=∠DFC . ∴BE=AB =6，CF=DC =6. ∴BF =4.∴EF =2. …………………………………………………3分 ∵AD ∥BC ,∴△EFG ∽△ADG . ∴15EG EF AG AD ==. ∴145EG EG =-. ∴EG=23.∴AG=103. ……………………………………………………4分由（1）知∠FGE=∠AGD=90°，由勾股定理，得DG=3，FG=3.∴DF=. …………………………………………………5分19. （昌平区2013年一模）在△ABC 中，AB =4，BC =6，∠ACB =30°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1． （1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数； （2）如图2，连接AA 1，CC 1．若△CBC 1的面积为3，求△ABA 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转的过程中，点P 的对应点是点P 1，直接写出线段EP 1长度的最大值与最小值．C 1C BA 1A图2A 1C 1ABC图1图3A解：（1）如图1，依题意得：△A 1C 1B ≌△ACB .……… 1分∴BC 1=BC ，∠A 1C 1B =∠C =30°. ∴∠BC 1C = ∠C =30°.∴∠CC 1A 1 = 60°.…………………………… 2分 （2）如图2，由（1）知：△A 1C 1B ≌△ACB .∴A 1B = AB ，BC 1 = BC ，∠A 1BC 1 =∠ABC . ∴∠1 = ∠2，114263A B AB C B BC === ∴ △A 1BA ∽△C 1BC ………………… 3分 ∴112ΔΔ2439A BA C BCS S ⎛⎫== ⎪⎝⎭. ……………………4分 ∵1Δ3C BC S =， ∴1Δ43A BA S =. ……………………………5分 （3）线段EP 1长度的最大值为8，EP 1长度的最小值1. ………… 7分20. （昌平区2013年一模）如图，在平面直角坐标系xOy 中，点B ，C 在x 轴上，点A ，E 在y 轴上，OB ︰OC =1︰3，AE =7，且tan ∠OCE =3，tan ∠ABO =2. （1）求经过A ，B ，C 三点的抛物线的解析式；（2）点D 在（1）中的抛物线上，四边形ABCD 是以BC 为一底边的梯形，求经过B 、D 两点的一次函数解析式； （3）在（2）的条件下，过点D 作直线DQ ∥y 轴交线段CE 于点Q ，在抛物线上是否存在点P ，使直线PQ 与坐标轴相交所成的锐角等于梯形ABCD 的底角，若存在，求出点P 的坐标；若不存在，请说明理由.解：（1）依题意得：∠AOB =∠COE =90°，∴OA OB =tan ∠ABO =2,OE=OCtan ∠OCE =3. …………………………………………1分 ∴OA =2OB ,OE =3OC . ∵OB =OC =1︰3, ∴OC =3OB . ∴OE =9OB .21C 1CBA 1A图2∵ AE =7, ∴9OB -2OB =7.∴OB =1,OC =3,OA =2,OE =9.∴A (0,2),B (-1,0),C (3,0),E (0,9).……………………………………………………2分设抛物线的解析式为：y =a (x +1)(x -3),∴ 2=-3a ，即a =-23.∴抛物线解析式为：224233y x x =-++.…………………………………3分（2）过点A 作AD ∥x 轴交抛物线于点D .∴ 2D A y y ==.∴D (2,2). …………………………………………4分 设直线BD 的解析式为y =kx +b ， ∴022k bk b=-+⎧⎨=+⎩∴k=23, b =23. ∴直线BD 的解析式为2233y x =+.…………………………………………5分 （3）易知直线CE 的解析式为y = -3x + 9, Q (2,3). 设与y 轴交于点F ，过点Q 作QM ⊥y 轴于点M . 则∠QMF =∠AOB = 90°. ∵∠QFM =∠ABO ， ∴tan ∠QFM = tan ∠ABO =2 . ∴2QM MF=.∵Q (2,3)， ∴1132MF QM ,MO ===.∴F (0,2)即P (0,2).经验证，P (0,2)在抛物线224233y x x =-++上. 易求得，此时直线PQ 的解析式为122y x =+，直线PQ 与抛物线224233y x x =-++的另一个交点的坐标为52148,⎛⎫⎪⎝⎭. ……………………………………………7分同理可求得满足条件的另两个点P 的坐标为22-⎝和22-⎝. ……………………………………9分 综上所述，满足条件的点P 的坐标为 P 1(0,2), P 252148,⎛⎫⎪⎝⎭，P32,-, P42-. 21. （朝阳2013年一模）掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，掷得面朝上 的点数大于4的概率为（ ） A ．61 B ．31 C ．41 D ．21答案：B22. （朝阳2013年一模）把方程2630x x ++=化成()2x n m +=的形式，正确的结果为（ ）A ．()236x += B ．()236x -= C ．()2312x += D ．()2633x += 答案：A23. （朝阳2013年一模）如图，AB 为⊙O 的弦，半径OC ⊥AB 于点D ，AB =32，∠B =30°， 则△AOC 的周长为 . 答案：624. （朝阳2013年一模）计算：()0223tan 602013--︒+．解：原式1314=-- ……………………………………………………4分 34=-.…………………………………………………………………………5分 25. （朝阳2013年一模）如图，在平面直角坐标系xOy 中，一次函数y = -x 的图象 与反比例函数()0ky x x=<的图象相交于点()4A m -，． （1）求反比例函数ky x=的解析式；（2）若点P 在x 轴上，AP =5，直接写出点P 的坐标．（1）解:把()4A m -，代入y = -x ，得m =4.……………………………………………1分 ∴()44A -，. ………………………………………………………………………………2分 把()44A -，代入ky x=，得k = -16. ∴反比例函数解析式为16y x=-. ………………………………………………………3分 （2）（-7，0）或（-1，0）.………………………………………………………………5分26. （朝阳2013年一模）如图，在四边形ABCD 中，∠D =90°，∠B =60°，AD =6，AB=3，AB ⊥AC ,在CD 上选取一点E ，连接AE ，将△ADE 沿AE 翻折，使点D 落在AC 上的点F 处． 求（1）CD 的长； （2）DE 的长． 解：（1）∵AB ⊥AC ，∴∠BAC =90°.∵∠B =60°，AB， ∴AC =10. ………………………………………………………………………1分 ∵∠D =90°,AD =6，∴CD =8. ………………………………………………………………………2分 （2）由题意，得∠AFE =∠D=90°，AF=AD =6， EF=DE .∴∠EFC =90°,∴FC =4. … ……………………………………………………………………3分 设DE =x ,则EF=x ,CE=8-x .在Rt △EFC 中，由勾股定理,得 2224(8)x x +=-.………………………4分 解得x =3.所以DE =3. ……………………………………………………………………5分27. （朝阳2013年一模）如图，⊙O 是△ABC 是的外接圆，BC 为⊙O 直径，作∠CAD =∠B ，且点D 在BC 的延长线上．(1)求证：直线AD 是⊙O 的切线； (2)若sin ∠CAD=4，⊙O 的半径为8，求CD 长． （1）证明：连接OA .∵BC 为⊙O 的直径，∴∠BAC =90°. (1)∴∠B +∠ACB =90°.∵OA=OC ，∴∠OAC =∠OCA . ∵∠CAD =∠B ， ∴∠CAD +∠OAC =90°. 即∠OAD =90°. ∴OA ⊥AD .∴AD 是⊙O 的切线. ……………………………………………………………………2分 (2) 解：过点C 作CE ⊥AD 于点E . ∵∠CAD =∠B ,∴sinB =sin ∠CAD .………………………………………………………………3分 ∵⊙O 的半径为8， ∴BC=16.∴AC =sin BC B ⋅= B B∴在Rt △ACE 中，CE=sin AC CAD ⋅∠=2.…………………………………………4分 ∵CE ⊥AD ,∴∠CED =∠OAD =90°.∴CE ∥OA .∴△CED ∽△OAD .∴CD CEOD OA=. 设CD =x ，则OD =x +8. 即288x x =+. 解得x =83.所以CD =83.………………………………………………………………………………5分28. （朝阳2013年一模）二次函数2134y x x n =++-的图象与x 轴只有一个交点；另一个二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交于两点，这两个交点的横坐标都是整数，且m 是小于5的整数． 求（1）n 的值；（2）二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交点的坐标． 解：(1)∵2134y x x n =++-的图象与x 轴只有一个交点， ∴令10y =，即2304x x n ++-=.……………………………………………1分∴131404n ⎛⎫∆=--= ⎪⎝⎭. 解得n =1. ………………………………………………………………………2分 (2)由(1)知，()2222146y x m x m m =--+-+.∵()2222146y x m x m m =--+-+的图象与x 轴有两个交点，∴[]2222(1)4(46)m m m ∆=----+820m =-.∵20∆>，∴52m >.……………………………………………………………………………3分 又∵5m <且m 是整数，∴m =4或3. …………………………………………………………………………5分 当m =4时，2266y x x =-+的图象与x 轴的交点的横坐标不是整数；当m =3时，2243y x x =-+，令20y =，即2430x x -+=，解得11x =，23x =.综上所述，交点坐标为（1，0），（3，0）. ………………………………………7分29. （朝阳2013年一模）在Rt △ABC 中，∠A =90°，D 、E 分别为AB 、AC 上的点．B（1）如图1，CE =AB ，BD =AE ，过点C 作CF ∥EB ，且CF =EB ，连接DF 交EB 于点G ，连接BF ，请你直接写出EBDC的值；（2）如图2，CE =kAB ，BD =kAE ，12EB DC =，求k 的值．解：(1)EB DC =………………………………………………………………………2分 (2)过点C 作CF ∥EB 且CF =EB ，连接DF 交EB 于点G , 连接BF .∴四边形EBFC 是平行四边形. …………………………………………………3分 ∴CE ∥BF 且CE =BF . ∴∠ABF =∠A =90°.∵BF =CE =kAB .∴BFk AB=. ∵BD =kAE ，∴BDk AE=.… ……………………………………………………………………4分 ∴BF BDAB AE=. ∴DBF ∆∽EAB ∆. ……………………………………………………………5分 ∴DF k BE=,∠GDB=∠AEB . ∴∠DGB =∠A =90°. ∴∠GFC =∠BGF =90°. ∵12CF EB DC DC ==.∴DF DF EB CF==. ∴k…………………………………………………………………………7分30. （朝阳2013年一模）如图，二次函数y =ax 2+2ax +4的图象与x 轴交于点A 、B ，与y 轴交于点C ，∠CBO 的正切值是2．(1)求此二次函数的解析式．(2)动直线l 从与直线AC 重合的位置出发，绕点A 顺时针旋转，与直线AB 重合时终止运动，直线l 与BC 交于点D ，P 是线段AD 的中点．①直接写出点P 所经过的路线长．②点D 与B 、C 不重合时，过点D 作DE ⊥AC 于点E 、作DF ⊥AB 于点F ，连接PE 、PF ，在旋转过程中，∠EPF 的大小是否发生变化？若不变，求∠EPF 的度数；若变化，请说明理由． ③在②的条件下，连接EF ，求EF 的最小值．图2B 图1FBB解：(1)根据题意，C (0，4)．∴OC =4．∵tan∠CBO =2，∴OB =2．∴B (2，0)．………………………………………………………………………1分∴ 0444a a =++．∴12a =-． ∴二次函数的解析式为2142y x x =--+．……………………………………2分(2) ①点P……………………………………………3分 ②∠EPF 的大小不发生改变．………………………………………………………4分 由2142y x x =--+可得，A (-4，0)． ∴OA = OC ．∴△AOC 是等腰直角三角形． ∴∠CAO =45°．∵DE ⊥AC ， DF ⊥AB ， ∴∠AED = ∠AFD =90°． ∵点P 是线段AD 的中点， ∴PE = PF =12AD = AP ． ∴∠EPD =2∠EAD ，∠FPD =2∠FAD ．∴∠EPF =∠EPD +∠FPD =2∠EAD +2∠FAD = 2∠CAO =90°．…………………5分 ③由②知，△EPF 是等腰直角三角形． ∴EF．……………………………………………………………6分 ∴当AD ⊥BC 时，AD 最小，此时EF 最小．……………………………………7分 在Rt△ABD 中，∵tan∠CBO =2，AB =6， ∴AD=5． ∴EF=5． 即此时EF．……………………………………………………8分 31.。

北京市各区2013年高三期末和一模数学理科分类-----第7、8和13、14题一、 选择题〔2013朝阳一摸理〕〔7〕抛物线22y px =〔p ＞0〕的焦点为F ，已知点A ，B 为抛物线上的两个动点，且满足120AFB ∠=︒.过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则||||MN AB 的最大值为 A. 33 B. 1 C. 33D. 2 〔2013朝阳一摸理〕〔8〕已知函数*()21,f x x x =+∈N .假设*0,x n ∃∈N ，使000()(1)()63f x f x f x n +++++=成立，则称0(,)x n 为函数()f x 的一个“生成点”.函数()f x 的“生成点”共有A. 1个 B .2个 C .3个 D .4个〔2013大兴一摸理〕〔7〕假设实数,a b 满足221a b ≤，则关于x 的方程220x x a b 无．实数根的概率为 〔A 〕14 〔B 〕 34 〔C 〕3π24π〔D 〕π24π 〔2013大兴一摸理〕〔8〕抛物线2(22)y x x ≤≤绕y 轴旋转一周形成一个如下列图的旋转体，在此旋转体内水平放入一个正方体，使正方体的一个面恰好与旋转体的开口面平齐，则此正方体的棱长是 〔A 〕1 〔B 〕2 〔C 〕22 〔D 〕4〔2013东城一摸理〕〔7〕已知定义在R 上的函数()f x 的对称轴为3x =-，且当3x ≥-时，()23x f x =-.假设函数()f x 在区间(1,)k k -〔k ∈Z 〕上有零点，则k 的值为 A〔A 〕2或7- 〔B 〕2或8- 〔C 〕1或7- 〔D 〕1或8-〔2013东城一摸理〕〔8〕已知向量OA ，AB ，O 是坐标原点，假设AB k OA =，且AB 方向是沿OA 的方向绕着A 点按逆时针方向旋转θ角得到的，则称OA 经过一次(,)k θ变换得到AB .现有向量=(1,1)OA 经过一次11(,)k θ变换后得到1AA ，1AA 经过一次22(,)k θ变换后得到12A A ，…，如此下去，21n n A A --经过一次(,)n n k θ变换后得到1n n A A -.设1(,)n n A A x y -=，112n n θ-=，1cos n nk θ=， 则y x -等于〔A 〕1112sin[2()]211sin1sin sin 22n n --- 〔B 〕1112sin[2()]211cos1cos cos 22n n --- 〔C 〕1112cos[2()]211sin1sin sin 22n n --- 〔D 〕1112cos[2()]211cos1cos cos 22n n ---〔2013房山一摸理〕7.某三棱椎的三视图如下列图，该三棱锥的四个面的面积中，最大的是A. 43B. 8C. 47D. 83〔2013房山一摸理〕M 是R 的子集，如果点0x ∈R 满足：00,,0a x M x x a ∀>∃∈<-<，称0x 为集合M 的聚点.则以下集合中以为聚点的有：① {|}1n n n ∈+N ； ②*2{|}n n ∈N ； ③Z ； ④{|2}x y y = A.①④ B. ②③ C. ①② D. ①②④〔2013丰台一摸理〕7. 如果函数y=f(x)图像上任意一点的坐标〔x,y 〕都满足方程 lg()lg lg x y x y +=+，那么正确的选项是(A) y=f(x)是区间〔0，+∞〕上的减函数，且x+y 4≤(B) y=f(x)是区间〔1，+∞〕上的增函数，且x+y 4≥(C) y=f(x)是区间〔1，+∞〕上的减函数，且x+y 4≥(D) y=f(x)是区间〔1，+∞〕上的减函数，且x+y 4≤〔2013丰台一摸理〕8．动圆C 经过点F(1,0)，并且与直线x=-1相切，假设动圆C 与直线221y x =++总有公共点，则圆C 的面积(A) 有最大值8π (B) 有最小值2π (C) 有最小值3π (D) 有最小值4π〔2013门头沟一摸理〕7．一个几何体的三视图如右图所示，则该几何体的体积是(A)21 (B) 13 (C)65 (D) 5〔2013门头沟一摸理〕8．定义在 R 上的函数()y f x =是减函数，且函数(2)y f x =+主视图 1 左视图 1 俯视图1的图象关于点(2,0)-成中心对称，假设,s t 满足不等式组()(2)0()0f t f s f t s +-≤⎧⎨-≥⎩，则当23s ≤≤时，2s t +的取值范围是(A) [3,4] (B) [3,9] (C) [4,6] (D) [4,9]〔2013西城一摸理〕7．已知函数22()log 2log ()f x x x c =-+，其中0c >．假设对于任意的(0,)x ∈+∞，都有()1f x ≤，则c 的取值范围是〔A 〕1(0,]4 〔B 〕1[,)4+∞ 〔C 〕1(0,]8 〔D 〕1[,)8+∞ 〔2013西城一摸理〕8．如图，正方体1111ABCD A BC D -中，P 为底面ABCD 上的动点，1PE AC ⊥于E ，且PA PE =，则点P 的轨迹是 〔A 〕线段〔B 〕圆弧 〔C 〕椭圆的一部分 〔D 〕抛物线的一部分〔2013延庆一摸理〕7.一四面体的三视图如下列图，则该四面体四个面中最大的面积是A.2B. 22C.3D. 32〔2013延庆一摸理〕8.已知函数)0(2)(23≠-+=a bx ax x f 有且仅有两个不同的零点1x ，2x ，则A ．当0<a 时，021<+x x ，021>x x B. 当0<a 时，021>+x x ，021<x xC. 当0>a 时，021<+x x ，021>x xD. 当0>a 时，021>+x x ，021<x x〔2013海淀一摸理〕7. 抛物线24y x =的焦点为F ，点(,)P x y 为该抛物线上的动点，又点(1,0)A -，则||||PF PA 的最 小值是A.12B.22C.32D.223〔2013海淀一摸理〕8. 设123,,l l l 为空间中三条互相平行且两两间的距离分别为4，5，6的直线.给出以下三个结论： ①i i A l ∃∈(1,2,3)i =，使得123A A A ∆是直角三角形；②i i A l ∃∈(1,2,3)i =，使得123A A A ∆是等边三角形；① 条直线上存在四点(1,2,3,4)i A i =，使得四面体1234A A A A 为在一个顶点处的三条棱两两互相垂直的四面体.其中，所有正确结论的序号是〔7题图〕A. ①B.①②C. ①③D. ②③〔2013石景山一摸理〕7．对于直线:(1)l y k x =+与抛物线2:4C y x =，1k =±是直线l 与抛物线C 有唯一交点的〔 〕条件A. 充分不必要B. 必要不充分C. 充要条件D. 既不充分也不必要〔2013石景山一摸理〕8．假设直角坐标平面内的两点P 、Q 满足条件：①P 、Q 都在函数)(x f y =的图像上；②P 、Q 关于原点对称.则称点对[P , Q ]是函数)(x f y =的一对“友好点对”〔注：点对[P , Q ]与[Q , P ]看作同一对“友好点对”〕.已知函数⎩⎨⎧≤-->=)0(4)0(log )(22x x x x x x f ，则此函数的“友好点对”有〔 〕对 A. 0 B. 1 C. 2 D. 3(2013昌平高三期末理)〔7〕已知一个空间几何体的三视图如下列图，根据图中标出的尺寸，可得这个几何体的全面积为A. 104342+ B ．102342+C. 142342+ D. 144342+(2013昌平高三期末理)〔8〕已知函数：①2()2f x x x =-+，②()cos()22x f x ππ=-，③12()|1|f x x =-.则以下四个命题对已知的三个函数都能成立的是命题:p ()f x 是奇函数； 命题:q (1)f x +在(0)，1上是增函数；命题:r 11()22f >； 命题:s ()f x 的图像关于直线1x =对称 A ．命题p q 、 B ．命题q s 、 C ．命题r s 、 D ．命题p r 、(2013朝阳高三期末理)7.设集合{}2A=230x x x +->，集合{}2B=210,0x x ax a --≤>.假设A B 中恰含有一个整数，则实数a 的取值范围是A ．30,4⎛⎫ ⎪⎝⎭ B ．34,43⎡⎫⎪⎢⎣⎭ C ．3,4⎡⎫+∞⎪⎢⎣⎭D ．()1,+∞ (2013朝阳高三期末理)8. 在棱长为1的正方体1111ABCD A BC D -中，点1P，2P 分别是线段AB ，1BD 〔不包括端点〕上的动点，且线段12P P 平行于平面11A ADD ，则四面体121PPAB 的体积的最大值是 A ．124 B ．112 C ．16 D ．12(2013东城高三期末理)〔7〕已知抛物线22y px =的焦点F 与双曲线22179x y -=的右焦点重合，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且||2|AK AF ，则△AFK 的面积为〔A 〕4 〔B 〕8 〔C 〕16 〔D 〕32(2013东城高三期末理)〔8〕给出以下命题：①在区间(0,)+∞上，函数1y x -=,12y x =,2(1)y x =-,3y x =中有三个是增函数；②假设log 3log 30m n <<，则01n m <<<；③假设函数()f x 是奇函数，则(1)f x -的图象关于点(1,0)A 对称；④已知函数233,2,()log (1),2,x x f x x x -⎧≤=⎨->⎩则方程 1()2f x =有2个实数根，其中正确命题的个数为〔A 〕1 〔B 〕2 〔C 〕3 〔D 〕4(2013丰台高三期末理)7．在平面直角坐标系xOy 中，已知A(1,0)，B 〔0,1〕，点C 在第二象限内，56AOC π∠=，且|OC|=2，假设OC OA OB λμ=+，则λ，μ的值是〔 〕(A)1 (B) 1(C) -11(2013丰台高三期末理)8．已知函数f(x)=2ax bx c ++,且,0a b c a b c >>++=，集合A={m|f(m)<0}，则(A) ,m A ∀∈都有f(m+3)>0 (B) ,m A ∀∈都有f(m+3)<0(C) 0,m A ∃∈使得f(m 0+3)=0 (D) 0,m A ∃∈使得f(m 0+3)<0(2013石景山高三期末理)7．某三棱锥的三视图如下列图，该三棱锥的体积是〔A ．38B ．4C ．2D ．34(2013石景山高三期末理)8. 在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[]k ，即[]{}5k n k n =+∈Z ，0,1,2,3,4k =．给出如下四个结论：① []20133∈； ② []22-∈； ③ [][][][][]01234Z =∪∪∪∪；④ 整数,a b 属于同一“类”的充要条件是“[]0a b -∈”．其中，正确结论的个数为〔 〕．A ．1B ．2C ．3D ．4(2013通州高三期末理)7．在ABC ∆中，角,,A B C 的对边分别为,,a b c ，则“2cos a b C =”是“ABC ∆是等腰三角形”的〔A 〕充分不必要条件 〔B 〕必要不充分条件 〔C 〕充分必要条件 〔D 〕既不充分也不必要条件(2013通州高三期末理)8．已知直线1:4360l x y -+=和直线2:1l x =-，抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是〔A 〕355 〔B 〕2 〔C 〕115 〔D 〕3 (2013海淀高三期末理)7. 用数字0,1,2,3组成数字可以重复的四位数, 其中有且只有一个数字出现两次的四位数的个数为A. 144B.120C. 108D.72(2013海淀高三期末理)8. 椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ，假设椭圆C 上恰好有6个不同的点P ，使得12F F P ∆为等腰三角形，则椭圆C 的离心率的取值范围是A.12(,)33B.1(,1)2C. 2(,1)3D.111(,)(,1)322二、填空题：〔2013朝阳一摸理〕〔13〕函数)(x f 是定义在R 上的偶函数，且满足(2)()f x f x +=.当[0,1]x ∈时，()2f x x =.假设在区间[2,3]-上方程2()0ax a f x +-=恰有四个不相等的实数根，则实数a 的取值范围是 .〔2013朝阳一摸理〕〔14〕在平面直角坐标系xOy 中，已知点A 是半圆2240x x y -+=〔2≤x ≤4〕上的一个动点，点C 在线段OA 的延长线上．当20OA OC ⋅=时，则点C 的纵坐标的取值范围是 ． 〔2013大兴一摸理〕〔13〕已知函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x 在区间[1,]m 上的最大值是1，则m 的取值范围是 ． 〔2013大兴一摸理〕〔14〕已知函数()f x 是定义在(0,)上的单调递增函数，且N x()N f x ，假设[()]3f f n n ，则(2)=f ；(4)(5)f f〔2013东城一摸理〕〔13〕有甲、乙、丙在内的6个人排成一排照相，其中甲和乙必须相邻，丙不排在两头，则这样的排法共有 种． 144〔2013东城一摸理〕〔14〕数列{a n }的各项排成如下列图的三角形形状，其中每一行比上一行增加两项，假设n n a a =(0)a ≠，则位于第10行的第8列的项等于 ，2013a 在图中位于 ．〔填第几行的第几列〕〔2013房山一摸理〕100天内的单价()f t 与时间的函数关系是22(040,)4()52(40100,)2t t t f t t t t ⎧+≤<∈⎪⎪=⎨⎪-+≤≤∈⎪⎩N N 日销售量()g t 与时间的函数关系是109()(0100,)33t g t t t =-+≤≤∈N .则这种商品的日销售额的最大值为 . 〔2013房山一摸理〕14.已知函数()f x 的定义域是D ，假设对于任意12,x x D ∈，当12x x <时，都有12()()f x f x ≤，则称函数()f x 在D 上为非减函数.设函数()f x 在[0,1]上为非减函数，且满足以下三个条件：①(0)0f =； ②1()()52x f f x =； ③(1)1()f x f x -=-.则4()5f = ，1()2013f = . 〔2013丰台一摸理〕13.某四面体的三视图如下列图，则该四面体的四个面中，直角三角形的面积和是_______. 〔2013丰台一摸理〕14. 已知M 是集合{}1,2,3,,21(*,2)k k N k -∈≥的非空子集，且当x M ∈时，有2k x M -∈.记满足条件的集合M 的个数为()f k ，则(2)f = ；()f k = 。

北京2013届高三最新模拟试题分类汇编（含9区一模及上学期期末试题精选）专题：数列一、选择题1 ．（2013届北京丰台区一模理科）设n S 为等比数列{}n a 的前n 项和，3420a a +=，则31S a （ ） A ．2B ．3C ．4D ．52 ．（2013届北京西城区一模理科）等比数列{}n a 中，10a >，则“13a a <”是“36a a <”的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3 ．（2013届东城区一模理科）已知数列{}n a 中，12a =，120n n a a +-=，2log n n b a =，那么数列{}n b 的前10项和等于 （ ）A ．130B ．120C ．55D ．504 ．（2013届房山区一模理科数学）已知{}n a 为等差数列，n S 为其前n 项和.若19418,7a a a ，则10S （ ）A ．55B ．81C ．90D ．1005 ．（北京市东城区普通高中示范校2013届高三3月联考综合练习（二）数学（理）试题 ）已知数列{}n a 满足*7(13)10,6(),6--+≤⎧=∈⎨>⎩N n n a n a n a n a n ，若{}n a 是递减数列，则实数a 的取值范围是 （ ） A ．⎝ ⎛⎭⎪⎫13，1 B ．⎝ ⎛⎭⎪⎫13，12 C ．⎝ ⎛⎭⎪⎫58，1 D ．⎝ ⎛⎭⎪⎫13，58 6 ．（北京市东城区2013届高三上学期期末考试数学理科试题）已知{}n a 为等差数列，其前n 项和为n S ，若36a =，312S =，则公差d 等于（ ）A ．1B ．53C ．2D ．37 ．（北京市海淀区北师特学校2013届高三第四次月考理科数学）已知正项数列{}n a 中，11=a ，22=a ，222112(2)n n n a a a n +-=+≥，则6a 等于（ ）A ．16B ．8C ．22D ．48 ．（北京市昌平区2013届高三上学期期末考试数学理试题 ）设n S 是公差不为0的等差数列{}n a 的前n 项和，且124,,S S S 成等比数列，则21a a 等于 （ ）A ．1B ．2C ．3D ．4二、填空题9 ．（2013届北京海滨一模理科）等差数列{}n a 中,34259,18a a a a +==, 则16_____.a a =10．（2013届北京市延庆县一模数学理）以下是面点师一个工作环节的数学模型：如图，在数轴上截取与闭区间]4,0[对应的线段，对折后（坐标4所对应的点与原点重合）再均匀地拉成4个单位长度的线段，这一过程称为一次操作（例如在第一次操作完成后，原来的坐标1、3变成2，原来的坐标2变成4，等等）.那么原闭区间]4,0[上（除两个端点外）的点，在第n 次操作完成后)1(≥n ，恰好被拉到与4重合的点所对应的坐标为)(n f ，则=)3(f ；=)(n f .11．（2013届北京西城区一模理科）设等差数列{}n a 的公差不为0，其前n 项和是n S ．若23S S =，0k S =，则k =______．12．（2013届北京西城区一模理科）记实数12,,,n x x x 中的最大数为12max{,,,}n x x x ，最小数为12min{,,,}n x x x .设△ABC 的三边边长分别为,,a b c ，且a b c ≤≤，定义△ABC 的倾斜度为max{,,}min{,a b c a t b c a b =⋅,}b cc a．（ⅰ）若△ABC 为等腰三角形，则t =______；（ⅱ）设1a =，则t 的取值范围是______． 13．（2013届东城区一模理科）数列{a n }的各项排成如图所示的三角形形状，其中每一行比上一行增加两项，若nn a a =(0)a ≠， 则位于第10行的第8列的项等于 ，2013a 在图中位于 ．（填第几行的第几列） 14．（2013届门头沟区一模理科）在等差数列{}n a 中，13a =，42a =，则4731n a a a ++++等于 ．15．（北京市东城区2013届高三上学期期末考试数学理科试题）定义映射:f A B →，其中{(,),}A m n m n =∈R ，B =R ，已知对所有的有序正整数对(,)m n 满足下述条件:①(,1)1f m =；②若n m >，(,)0f m n =；③(1,)[(,)(,1)]f m n n f m n f m n +=+-， 则(2,2)f = ，(,2)f n = ．16．（北京市海淀区北师特学校2013届高三第四次月考理科数学）对任意x ∈R ，函数()f x 满足0 2 4（14题21(1)()[()]2f x f x f x+=-+，设)()]([2nfnfan-=，数列}{na的前15项的和为3116-，则(15)f=．17．（北京市西城区2013届高三上学期期末考试数学理科试题）设等比数列{}na的各项均为正数，其前n项和为nS．若11a=，34a=，63kS=，则k=______．18．（北京市丰台区2013届高三上学期期末考试数学理试题）右表给出一个“三角形数阵”.已知每一列数成等差数列，从第三行起，每一行数成等比数列，而且每一行的公比都相等，记第i行第j列的数为ij a （*,,Nji ji∈≥），则53a等于，______(3)mna m=≥.19．（【解析】北京市朝阳区2013届高三上学期期末考试数学理试题）已知数列121,,,9a a是等差数列，数列1231,,,,9b b b是等比数列，则212ba a+的值为 .20．（【解析】北京市朝阳区2013届高三上学期期末考试数学理试题）将整数1,2,3,,25填入如图所示的5行5列的表格中，使每一行的数字从左到右都成递增数列，则第三列各数之和的最小值为，最大值为 .21．（【解析】北京市海淀区2013届高三上学期期末考试数学理试题）.数列{}n a满足12,a=且对任意的*,Nm n∈，都有n m nmaaa+=，则3_____;a={}na的前n项和nS=_____.22．（【解析】北京市石景山区2013届高三上学期期末考试数学理试题）在等比数列{}na中，141=,=42a a，则公比=q，123++++=na a a a23．（2013届北京大兴区一模理科）已知数列}{n a 的各项均为正整数，且12n a a a <<<，设集合1{|101}1，，或，或（≤≤）nk i iiiii A x x a k n λλλλ====-==∑。

北京市西城区2013年高三一模试卷高三数学（理科） 2013.4一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知全集U=R ，集合{|02}A x x =<<，2{|10}B x x =->，那么U AB =ð（A ）{|01}x x <<（B ）{|01}x x <≤ （C ）{|12}x x << （D ）{|12}x x ≤<2．若复数i2ia +的实部与虚部相等，则实数a = （A ）1- （B ）1（C ）2-（D ）23．执行如图所示的程序框图．若输出y =角=θ（A ）π6 （B ）π6-（C ）π3（D ）π3-4．从甲、乙等5名志愿者中选出4名，分别从事A ，B ，C ，D 四项不同的工作，每人承担一项．若甲、乙二人均不能从事A 工作，则不同的工作分配方案共有（A ）60种 （B ）72种（C ）84种（D ）96种5．某正三棱柱的三视图如图所示，其中正（主）视图是边长为2的正方形，该正三棱柱的表面积是 （A）6 （B）12+（C）12+ （D）24+6．等比数列{}n a 中，10a >，则“13a a <”是“36a a <”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件7．已知函数22()log 2log ()f x x x c =-+，其中0c >．若对于任意的(0,)x ∈+∞，都有()1f x ≤，则c 的取值范围是 （A ）1(0,]4（B ）1[,)4+∞ （C ）1(0,]8（D ）1[,)8+∞8．如图，正方体1111ABCD A B C D -中，P 为底面ABCD上的动点，1PE A C ⊥于E ，且PA PE =，则点P 的轨迹是 （A ）线段 （B ）圆弧（C ）椭圆的一部分（D ）抛物线的一部分第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分．9．已知曲线C 的参数方程为2cos 12sin x y =⎧⎨=+⎩αα（α为参数），则曲线C 的直角坐标方程为 ．10．设等差数列{}n a 的公差不为0，其前n 项和是n S ．若23S S =，0k S =，则k =______．11．如图，正六边形ABCDEF 的边长为1，则AC DB ⋅=______． 12．如图，已知AB 是圆O 的直径，P 在AB 的延长线上，PC切圆O 于点C ，CD OP ⊥于D ．若6CD =，10CP =， 则圆O 的半径长为______；BP =______． 13．在直角坐标系xOy 中，点B 与点(1,0)A -关于原点O 对称．点00(,)P x y 在抛物线24y x =上，且直线AP 与BP 的斜率之积等于2，则0x =______．14．记实数12,,,n x x x 中的最大数为12max{,,,}n x x x ，最小数为12min{,,,}n x x x .设△ABC的三边边长分别为,,a b c ，且a b c ≤≤，定义△ABC 的倾斜度为max{,,}min{,a b c at b c a b=⋅,}b cc a． （ⅰ）若△ABC 为等腰三角形，则t =______；（ⅱ）设1a =，则t 的取值范围是______．三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤． 15．（本小题满分13分）已知函数()sin cos f x x a x =-的一个零点是π4． （Ⅰ）求实数a 的值；（Ⅱ）设()()()cos g x f x f x x x =⋅-+，求()g x 的单调递增区间．16．（本小题满分13分）某班有甲、乙两个学习小组，两组的人数如下：现采用分层抽样的方法（层内采用简单随机抽样）从甲、乙两组中共抽取3名同学进行学业检测． （Ⅰ）求从甲组抽取的同学中恰有1名女同学的概率； （Ⅱ）记X 为抽取的3名同学中男同学的人数，求随机变量X的分布列和数学期望．17．（本小题满分14分）在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD ，BC AB 2=，60ABC ︒∠=，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ；（Ⅱ）求BC 与平面EAC 所成角的正弦值；（Ⅲ）线段ED 上是否存在点Q ，使平面EAC ⊥平面QBC ？ 证明你的结论．18．（本小题满分13分）已知函数()ln f x ax x =-，()e 3axg x x =+，其中a ∈R ．（Ⅰ）求)(x f 的极值；（Ⅱ）若存在区间M ，使)(x f 和()g x 在区间M 上具有相同的单调性，求a 的取值范围．19．（本小题满分14分）如图，椭圆22221(0)x y a b a b+=>>的左焦点为F ，过点F 的直线交椭圆于A ，B 两点．当直线AB 经过椭圆的一个顶点时，其倾斜角恰为60︒．（Ⅰ）求该椭圆的离心率； （Ⅱ）设线段AB 的中点为G ，AB 的中垂线与x 轴和y 轴分别交于,D E 两点．记△GFD 的面积为1S ，△OED （O 为原点）的面积为2S ，求12S S 的取值范围．20．（本小题满分13分）已知集合*12{|(,,,),,1,2,,}(2)n n i S X X x x x x i n n ==∈=≥N ．对于12(,,,)n A a a a =，12(,,,)n nB b b b S =∈，定义1122(,,,)nnAB b a b a b a =---； 1212(,,,)(,,,)()n n a a a a a a =∈R λλλλλ；A 与B 之间的距离为1(,)||ni i i d A B a b ==-∑．（Ⅰ）当5n =时，设5(1,2,1,2,)A a =，(2,4,2,1,3)B =．若(,)7d A B =，求5a ；（Ⅱ）（ⅰ）证明：若,,n A B C S ∈，且0∃>λ，使A B B C λ=，则(,)(,)(d A B d B C d A C+=； （ⅱ）设,,n A B C S ∈，且(,)(,)(,d A B d B C d A C +=．是否一定0∃>λ，使A B B C λ=？说明理由；（Ⅲ）记(1,1,,1)n I S =∈．若A ，n B S ∈，且(,)(,)d I A d I B p ==，求(,)d A B 的最大值．北京市西城区2013年高三一模试卷高三数学（理科）参考答案及评分标准2013.4一、选择题：本大题共8小题，每小题5分，共40分.1． B ； 2．A ； 3．D ； 4．B ； 5．C ； 6．B ； 7．D ； 8．A ．二、填空题：本大题共6小题，每小题5分，共30分.9．22230xy y +--=； 10．5； 11．32-12．152，5； 13．1+ 14．1，． 注：12、14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分. 15．（本小题满分13分） （Ⅰ）解：依题意，得π()04f =， ………………1分 即ππsincos 04422a -=-=， ………………3分 解得1a =． ………………5分（Ⅱ）解：由（Ⅰ）得()sin cos f x x x =-． ………………6分()()()cos g x f x f x x x =⋅-+(sin cos )(sin cos )2x x x x x =--- (7)分22(cos sin )2x x x =-+ ………………8分cos 22x x =+ ………………9分π2sin(2)6x =+． ………………10分由 πππ2π22π262k x k -≤+≤+，得 ππππ36k x k -≤≤+，k ∈Z ． ………………12分所以 ()g x 的单调递增区间为ππ[π,π]36k k -+，k ∈Z ． ………………13分16．（本小题满分13分）（Ⅰ）解：依题意，甲、乙两组的学生人数之比为 (35):(22)2:1++=， ……………1分所以，从甲组抽取的学生人数为2323⨯=；从乙组抽取的学生人数为1313⨯=．………2分 设“从甲组抽取的同学中恰有1名女同学”为事件A ， ………………3分则 113528C C 15()C 28P A ⋅==，故从甲组抽取的同学中恰有1名女同学的概率为1528． ………………5分 （Ⅱ）解：随机变量X 的所有取值为0,1,2,3． ………………6分21522184C C 5(0)C C 28P X ⋅===⋅， 111213525221218484C C C C C 25(1)C C C C 56P X ⋅⋅⋅==+=⋅⋅， 211113235221218484C C C C C 9(2)C C C C 28P X ⋅⋅⋅==+=⋅⋅， 21322184C C 3(3)C C 56P X ⋅===⋅．……………10分所以，随机变量X的分布列为:………………11分5259350123285628564EX =⨯+⨯+⨯+⨯=． ………………13分17．（本小题满分14分） （Ⅰ）证明：因为BC AB 2=，60ABC ︒∠=，在△ABC 中，由余弦定理可得 BC AC 3=， 所以BC AC ⊥． ………………2分 又因为 AC FB ⊥，所以⊥AC 平面FBC ． ………………4分（Ⅱ）解：因为⊥AC 平面FBC ，所以FC AC ⊥．因为FC CD⊥，所以⊥FC 平面ABCD． ………………5分所以,,CA CF CB 两两互相垂直，如图建立的空间直角坐标系xyz C -． (6)分在等腰梯形ABCD 中，可得 CB CD =．设1BC =，所以11(0,0,0),(0,1,0),(,,0),(,,1)2222C A BDE --．所以)1,21,23(-=，)0,0,3(=，)0,1,0(=． 设平面EAC 的法向量为=()x,y,z n ，则有0,0.CE CA ⎧⋅=⎪⎨⋅=⎪⎩n n所以10,20.x y z -+=⎨= 取1z =，得=n (0,2,1)． ………………8分 设BC 与平面EAC 所成的角为θ，则||sin |cos ,|5||||CB CB CB ⋅=〈〉==θn n n ， 所以BC 与平面EAC 所成角的正弦值为552． ………………9分（Ⅲ）解：线段ED 上不存在点Q ，使平面EAC ⊥平面QBC ．证明如下： ………………10分假设线段ED 上存在点Q ，设 ),21,23(t Q - )10(≤≤t ，所以),21,23(t -=． 设平面QBC 的法向量为=m ),,(c b a ，则有0,0.CB CQ ⎧⋅=⎪⎨⋅=⎪⎩m m所以0,10.22b a b tc =⎧-+=⎪⎩ 取 1=c ，得=m )1,0,32(t -． ………………12分 要使平面EAC ⊥平面QBC ，只需0=⋅n m ，………………13分即 002110⨯+⨯+⨯=， 此方程无解． 所以线段ED 上不存在点Q ，使平面EAC ⊥平面QBC ． ………………14分18.（本小题满分13分） （Ⅰ）解：()f x 的定义域为(0,)+∞， ………………1分且11()ax f x a x x -'=-=． ………………2分 ① 当0a ≤时，()0f x '<，故()f x 在(0,)+∞上单调递减．从而)(x f 没有极大值，也没有极小值． ………………3分② 当0a >时，令()0f x '=，得1x a=． ()f x 和()f x '的情况如下：故()f x 的单调减区间为(0,)a ；单调增区间为(,)a +∞．从而)(x f 的极小值为1()1ln f a a=+；没有极大值． ………………5分（Ⅱ）解：()g x 的定义域为R ，且 ()e 3ax g x a '=+． ………………6分③ 当0a>时，显然 ()0g x '>，从而()g x 在R 上单调递增．由（Ⅰ）得，此时()f x 在1(,)a+∞上单调递增，符合题意． ………………8分④ 当0a=时，()g x 在R 上单调递增，()f x 在(0,)+∞上单调递减，不合题意．……9分⑤ 当0a <时，令()0g x '=，得013ln()x a a=-． ()g x 和()g x '的情况如下表：当30a -≤<时，00x ≤，此时()g x 在0(,)x +∞上单调递增，由于()f x 在(0,)+∞上单调递减，不合题意． ………………11分当3a <-时，00x >，此时()g x 在0(,)x -∞上单调递减，由于()f x 在(0,)+∞上单调递减，符合题意．综上，a 的取值范围是(,3)(0,)-∞-+∞． ………………13分19．（本小题满分14分） （Ⅰ）解：依题意，当直线AB 经过椭圆的顶点(0,)b 时，其倾斜角为60︒． ………………1分设(,0)F c -，则tan 60bc︒== ………………2分 将b = 代入 222a bc =+，解得2a c =． ………………3分所以椭圆的离心率为12c e a ==． ………………4分 （Ⅱ）解：由（Ⅰ），椭圆的方程可设为2222143x y c c +=． ………………5分 设11(,)A x y ，22(,)B x y ．依题意，直线AB 不能与,x y 轴垂直，故设直线AB 的方程为()y k x c =+，将其代入2223412x y c +=，整理得 222222(43)84120k x ck x k c c +++-=． (7)分则2122843ck x x k -+=+，121226(2)43cky y k x x c k +=++=+，22243(,)4343ck ck G k k -++． ………………8分 因为GD AB ⊥，所以2223431443Dckk k ck x k +⨯=---+，2243Dck x k -=+． ………………9分因为 △GFD ∽△OED ，所以2222222212222243()()||434343||()43ck ck ck S GD k k k ck S OD k ---++++==-+ (11)分222242222242(3)(3)99999()ck ck c k c k ck c k k++===+>． ………………13分所以12S S 的取值范围是(9,)+∞． ………………14分20．（本小题满分13分）（Ⅰ）解：当5n =时，由51(,)||7i i i d A B a b ==-=∑，得 5|12||24||12||21||3|7a -+-+-+-+-=，即 5|3|2a -=．由*5a ∈N ，得 51a =，或55a =． ………………3分（Ⅱ）（ⅰ）证明：设12(,,,)n A a a a =，12(,,,)n B b b b =，12(,,,)n C c c c =．因为 0∃>λ，使 AB BC λ=，所以 0∃>λ，使得 11221122(,,)((,,)n n n n b a b a b a c b c b c b ---=---λ,,，即0∃>λ，使得 ()i i i i b a c b λ-=-，其中1,2,,i n =．所以i i b a -与(1,2,,)i i c b i n -=同为非负数或同为负数． ………………5分所以 11(,)(,)||||nni i i i i i d A B d B C a b b c ==+=-+-∑∑1(||||)ni i i i i b a c b ==-+-∑1||(,)ni i i c a d A C ==-=∑． (6)分（ⅱ）解：设,,n A B C S ∈，且(,)(,)(,)d A B d B C d A C +=，此时不一定0∃>λ，使得AB BC λ=． ………………7分反例如下：取(1,1,1,,1)A =，(1,2,1,1,,1)B =，(2,2,2,1,1,,1)C ，则(,)1d A B =，(,)2d B C =，(,)3d A C =，显然(,)(,)(,)d A B d B C d A C +=． 因为(0,1,0,0,,0)AB =，(1,0,1,0,0,,0)BC =，所以不存在>0λ，使得AB BC λ=． ………………8分 （Ⅲ）解法一：因为1(,)||ni i i d A B b a ==-∑，设(1,2,,)ii b a i n -=中有()m m n ≤项为非负数，n m -项为负数．不妨设1,2,,i m=时0ii b a -≥；1,2,,i m m n =++时，0i i b a -<．所以 1(,)||ni i i d A B b a ==-∑12121212[()()][()()]m m m m n m m n b b b a a a a a a b b b ++++=+++-+++++++-+++因为 (,)(,)d I A d I B p ==，所以11(1)(1)nniii i a b ==-=-∑∑， 整理得 11nniii i a b ===∑∑．所以 12121(,)||2[()]ni i m m i d A B b a b b b a a a ==-=+++-+++∑． (10)分因为 121212()()m n m m n b b b b b b b b b +++++=+++-+++()()1p n n m p m ≤+--⨯=+；又 121m a a a m m +++≥⨯=， 所以 1212(,)2[()]m m d A B b b b a a a =+++-+++2[()]2p m m p ≤+-=．即 (,)2d A B p ≤． ……………12分 对于(1,1,,1,1)A p =+，(1,1,1,,1)B p =+，有A，nB S ∈，且(,)(,)d I A d I B p==，(,)2d A B p =．综上，(,)d A B 的最大值为2p ． ……………13分 解法二：首先证明如下引理：设,x y ∈R ，则有 ||||||x y x y +≤+．证明：因为 ||||x x x -≤≤，||||y y y -≤≤，所以 (||||)||||x y x y x y -+≤+≤+，即||||||x y x y +≤+．所以 11(,)|||(1)(1)|n ni i i i i i d A B b a b a ===-=-+-∑∑1(|1||1|)ni i i b a =≤-+-∑11|1||1|2n ni i i i a b p ===-+-=∑∑． (11)分上式等号成立的条件为1ia =，或1ib =，所以 (,)2d A B p ≤． ……………12分对于(1,1,,1,1)A p =+，(1,1,1,,1)B p =+，有A，nB S ∈，且(,)(,)d I A d I B p==，(,)2．d A B pd A B的最大值为2p．……………13分综上，(,)。

2013北京市语文中考各区一模试题汇编---名著阅读【2013东城一模】8.名著阅读（3分）孟子的文章感情强烈，气势充沛，说理充分。

比如，在《鱼我所欲也》中，以三个“乡为身死而不受”领起，表达了对贪求富贵，舍弃①的强烈谴责。

又如，在《②》中，文章开头列举了以③为首的六位历史人物奋起于苦难之中的事例，阐述了艰难困苦对于人才的作用，具有极强的说服力。

答案：①义②生于忧患，死于安乐③舜【2013西城一模】8.名著阅读（3分）“温故知新”一词出自《①》，“舍生取义”出自②家的另一部经典著作《孟子》。

在我们学过的一篇文章中，孟子用排比句式列举了舜、傅说、③（填一个人名）等承担“大任”者须经历各种磨难的事实，论证了“生于忧患，死于安乐”的观点。

答案：①论语②儒③胶鬲（管夷吾、孙叔敖、百里奚）【2013朝阳一模】8.名著阅读（3“他”再入一步，踏住胸脯，提起那醋钵儿大小拳头，看着这郑屠道：“洒家始投老种经略相公，做到关西五路廉访使，也不枉了叫做‘镇关西’!你是个卖肉的操刀屠户，狗一般的人，也叫做‘镇关西’!你如何强骗了金翠莲?”扑的只一拳，正打在鼻子上，打得鲜血迸流，鼻子歪在半边，却便似开了个油酱铺，咸的、酸的、辣的一发都滚出来。

选文出自名著《①》，作者是元末明初的小说家②。

文中“他”指的是○3。

答案：①水浒传(水浒) ②施耐庵③鲁达（鲁提辖）【2013丰台一模】8.名著阅读（3分）《①》与《大学》、《孟子》、《中庸》并称“四书”，是儒家的经典，包含政治主张、道德观念、教育原则等方面的内容。

孔子认为②（填成语）的学习方法可以在不断温习旧知识中受到启发，有新收获。

孟子认为道义尊严比生命更为重要，《鱼我所欲也》一文中③的故事论证的就是这个道理。

答案:①论语②温故知新③不受嗟来之食【2013石景山一模】8.名著阅读(3分)“那七个贩枣的客人，立于松树旁边，指着这一十五人说道：‘倒也！倒也！’只见这十五个人头重脚轻，一个个面面相觑，都软倒了。

海淀区高三年级第二学期期中练习数 学 （理科） 2013.4本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上 作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.集合2{6},{30}A x x B x x x =∈≤=∈->N|R|，则A B =A.{3,4,5}B.{4,5,6}C.{|36}x x <≤D.{|36}x x ≤< 2.在极坐标系中, 曲线4cos ρθ=围成的图形面积为Ａ. π B. 4 Ｃ. 4π Ｄ. 16 3.某程序的框图如图所示，执行该程序， 若输入的x 值为5，则输出的y 值为 Ａ. 2- B. 1- C.12D. 2 4.不等式组1,40,0x x y kx y ≥⎧⎪+-≤⎨⎪-≤⎩表示面积为1的直角三角形区域，则k 的值为Ａ. 2- B. 1- C. 0 D. 1 5. 若向量,a b 满足||||||1==+=a b a b ，则⋅a b 的值为 A. 12-B. 12C. 1-D. 16. 一个盒子里有3个分别标有号码为1，2，3的小球，每次取出一个，记下它的标号后再放回盒子中，共取3次，则取得小球标号最大值是3的取法有A. 12种B. 15种C. 17种D. 19种7. 抛物线24y x =的焦点为F ，点(,)P x y 为该抛物线上的动点，又点(1,0)A -，则||||PF PA 的最 小值是 A.12 B. 22 C. 32 D. 2238. 设123,,l l l 为空间中三条互相平行且两两间的距离分别为4，5，6的直线.给出下列三个结论： ①i i A l ∃∈(1,2,3)i =，使得123A A A ∆是直角三角形； ②i i A l ∃∈(1,2,3)i =，使得123A A A ∆是等边三角形；开始输出y结束输入x2-=x x0≤xx y 2=是否③三条直线上存在四点(1,2,3,4)i A i =，使得四面体1234A A A A 为在一个顶点处的三条棱两两互相垂直的四面体.其中，所有正确结论的序号是A. ①B.①②C. ①③D. ②③二、填空题:本大题共6小题,每小题5分,共30分.9. 在复平面上，若复数 + i a b （,a b ∈R ）对应的点恰好在实轴上，则b =_______. 10.等差数列{}n a 中,34259,18a a a a +==, 则16_____.a a = 11.如图， AP 与O 切于点A ，交弦DB 的延长线于点P ，过点B 作圆O 的切线交AP 于点C . 若90ACB ∠=︒，3,4BC CP ==，则弦DB 的长为_______.12.在ABC ∆中，若4,2,a b ==1cos 4A =-，则_____,sin ____.c C ==13.已知函数22, 0,()3, 0xa x f x x ax a x ⎧-≤⎪=⎨-+>⎪⎩有三个不同的零点，则实数a 的取值范围是_____.14.已知函数π()sin 2f x x =，任取t ∈R ，定义集合：{|t A y =()y f x =，点(,())P t f t ，(,())Q x f x 满足||2}PQ ≤.设, t t M m 分别表示集合t A 中元素的最大值和最小值，记()t t h t M m =-. 则 （1）函数()h t 的最大值是_____；（2）函数()h t 的单调递增区间为________.三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.（本小题满分13分）已知函数2()2(3sin cos )f x x x =--. （Ⅰ）求π()4f 的值和()f x 的最小正周期； （Ⅱ）求函数()f x 在区间[,]63ππ-上的最大值和最小值.DCBPAO在某大学自主招生考试中，所有选报II 类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A,B,C,D,E 五个等级. 某考场考生两科的考试成绩的数据统计如下图所示， 其中“数学与逻辑”科目的成绩为B 的考生有10人. （I ）求该考场考生中“阅读与表达”科目中成绩为A 的人数； （II ）若等级A ，B ，C ，D ，E 分别对应5分，4分，3分，2分，1分. （i ）求该考场考生“数学与逻辑”科目的平均分；(ii)若该考场共有10人得分大于7分，其中有2人10分，2人9分，6人8分. 从这10人中随机抽取两人，求两人成绩之和的分布列和数学期望.0.375等级频率0.2000.075科目：数学与逻辑0.025频率等级0.1500.375科目：阅读与表达17.（本小题满分14分）在四棱锥P ABCD -中，PA ⊥平面ABCD ，ABC ∆是正三角形，AC 与BD 的交点M 恰好是AC 中点，又4PA AB ==，120CDA ∠=，点N 在线段PB 上，且2PN =． （Ⅰ）求证：BD PC ⊥； （Ⅱ）求证：//MN 平面PDC ; （Ⅲ）求二面角A PC B --的余弦值．MDCBAPN已知函数2()ln f x x ax bx =++(其中,a b 为常数且0a ≠)在1x =处取得极值. (I) 当1a =时，求()f x 的单调区间；(II) 若()f x 在(]0,e 上的最大值为1，求a 的值.19.（本小题满分14分）已知圆M ：222(2)x y r -+=（0r >）.若椭圆C ：22221x y a b+=（0a b >>）的右顶点为圆M的圆心，离心率为22. （I ）求椭圆C 的方程；（II ）若存在直线l ：y kx =，使得直线l 与椭圆C 分别交于A ，B 两点，与圆M 分别交于G ，H两点，点G 在线段AB 上，且AG BH =，求圆M 半径r 的取值范围.20.（本小题满分13分）设(,),(,)A A B B A x y B x y 为平面直角坐标系上的两点，其中,,,A A B B x y x y ∈Z .令B A x x x ∆=-，B A y y y ∆=-，若x ∆+=3y ∆,且||||0x y ∆⋅∆≠，则称点B 为点A 的“相关点”，记作：()B A τ=. 已知0P 0000(,)(,)x y x y ∈ Z 为平面上一个定点，平面上点列{}i P 满足：1()i i P P τ-=，且点i P 的坐标为(,)i i x y ，其中1,2,3,...,i n =.（Ⅰ）请问：点0P 的“相关点”有几个？判断这些“相关点”是否在同一个圆上，若在同一个圆上，写出圆的方程；若不在同一个圆上，说明理由； （Ⅱ）求证：若0P 与n P 重合，n 一定为偶数；（Ⅲ）若0(1,0)P ，且100n y =， 记0ni i T x ==∑，求T 的最大值.海淀区高三年级第二学期期中练习数 学 （理）参考答案及评分标准 2013．4说明： 合理答案均可酌情给分，但不得超过原题分数. 一、选择题（本大题共8小题,每小题5分,共40分）题号 1 2 3 4 5 6 7 8 答案BCCDADBB二、填空题（本大题共6小题,每小题5分, 有两空的小题，第一空3分，第二空2分， 共30分）三、解答题(本大题共6小题,共80分) 15．（本小题满分13分）解：（I ）因为2()2(3sin cos )f x x x =--22= 2(3sin cos 23sin cos )x x x x -+-22(12sin 3sin2)x x =-+- ………………2分 2= 12sin 3sin2x x -+cos23sin2x x =+ ………………4分π= 2sin(2)6x + ………………6分所以πππ2π()2sin(2)2sin 34463f =⋅+== ………………7分 所以 ()f x 的周期为2π2π= π||2T ω== ………………9分 9． 010． 1411.24512．33, 151613． 491a <≤14． 2,(21,2), Z k k k -∈（II ）当ππ[,]63x ∈-时，π2π2[,]33x ∈-，ππ5π(2)[,]666x +∈- 所以当π6x =-时，函数取得最小值π()16f -=- ………………11分 当π6x =时，函数取得最大值π()26f = ………………13分 16.解：（Ｉ）因为“数学与逻辑”科目中成绩等级为B 的考生有10人， 所以该考场有100.2540÷=人 ………………1分所以该考场考生中“阅读与表达”科目中成绩等级为A 的人数为40(10.3750.3750.150.025)400.0753⨯----=⨯= ………………3分(II) 求该考场考生“数学与逻辑”科目的平均分为1(400.2)2(400.1)3(400.375)4(400.25)5(400.075)2.940⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=………………7分（Ⅲ）设两人成绩之和为ξ，则ξ的值可以为16，17，18，19，20 ………………8分2621015(16)45C P C ξ===， 116221012(17)45C C P C ξ===11262222101013(18)45C C C P C C ξ==+=， 11222104(19)45C C P C ξ=== 222101(20)45C P C ξ===所以ξ的分布列为X 16 17 18 19 20P1545 1245 1345 445145………………11分所以1512134186161718192045454545455E ξ=⨯+⨯+⨯+⨯+⨯= 所以ξ的数学期望为865………………13分17.证明：(I) 因为ABC ∆是正三角形，M 是AC 中点，所以BM AC ⊥,即BD AC ⊥ ………………1分 又因为PA ABCD ⊥平面，BD ⊂平面ABCD ，PA BD ⊥ ………………2分 又PA AC A = ，所以BD ⊥平面PAC ………………3分又PC ⊂平面PAC ，所以BD PC ⊥ ………………4分（Ⅱ）在正三角形ABC 中，23BM = ………………5分 在ACD ∆中，因为M 为AC 中点，DM AC ⊥，所以AD CD =120CDA ∠= ，所以233DM =，所以:3:1BM MD = ………………6分 在等腰直角三角形PAB 中，4PA AB ==，42PB =，所以:3:1BN NP =，::BN NP BM MD =，所以//MN PD ………………8分 又MN ⊄平面PDC ，PD ⊂平面PDC ，所以//MN 平面PDC ………………9分 （Ⅲ）因为90BAD BAC CAD ∠=∠+∠= ，所以AB AD ⊥，分别以,AB AD AP , 为x 轴, y 轴, z 轴建立如图的空间直角坐标系，所以43(4,0,0),(2,23,0),(0,,0),(0,0,4)3B C D P由（Ⅱ）可知，43(4,,0)3DB =- 为平面PAC 的法向量 ………………10分(2,23,4)PC =- ，(4,0,4)PB =-设平面PBC 的一个法向量为(,,)n x y z =,z yxMAD BCPN则00n PC n PB ⎧⋅=⎪⎨⋅=⎪⎩，即22340440x y z x z ⎧+-=⎪⎨-=⎪⎩， 令3,z =则平面PBC 的一个法向量为(3,3,3)n =………………12分设二面角A PC B --的大小为θ， 则7cos 7n DB n DBθ⋅==⋅所以二面角A PC B --余弦值为77………………14分 18. 解：（I ）因为2()ln ,f x x ax bx =++所以1()2f x ax b x'=++ ………………2分 因为函数2()ln f x x ax bx =++在1x =处取得极值(1)120f a b '=++= ………………3分 当1a =时，3b =-，2231()x x f x x-+'=，'(),()f x f x 随x 的变化情况如下表：x1(0,)2121(,1)21 1+∞（，）'()f x +0 -0 +()f x极大值极小值………………5分所以()f x 的单调递增区间为1(0,)2,1+∞（，）单调递减区间为1(,1)2………………6分(II)因为222(1)1(21)(1)()ax a x ax x f x x x-++--'==令()0f x '=,1211,2x x a==………………7分因为()f x 在 1x =处取得极值，所以21112x x a=≠= 当102a<时，()f x 在(0,1)上单调递增，在(1,e]上单调递减 所以()f x 在区间(]0,e 上的最大值为(1)f ，令(1)1f =，解得2a =-………………9分 当0a >，2102x a=> 当112a <时，()f x 在1(0,)2a 上单调递增，1(,1)2a上单调递减，(1,e)上单调递增 所以最大值1可能在12x a=或e x =处取得 而2111111()ln ()(21)ln 10222224f a a a a a a a a=+-+=--< 所以2(e)lne+e (21)e 1f a a =-+=，解得1e 2a =- ………………11分 当11e 2a≤<时,()f x 在区间(0,1)上单调递增，1(1,)2a 上单调递减，1(,e)2a 上单调递增所以最大值1可能在1x =或e x =处取得 而(1)ln1(21)0f a a =+-+< 所以2(e)lne+e (21)e 1f a a =-+=， 解得1e 2a =-，与211e 2x a<=<矛盾 ………………12分 当21e 2x a=≥时，()f x 在区间(0,1)上单调递增，在(1,e)单调递减， 所以最大值1可能在1x =处取得，而(1)ln1(21)0f a a =+-+<，矛盾综上所述，12a e =-或 2a =-. ……ABG H …………13分1９.（本小题满分14分） 解：（I ）设椭圆的焦距为2c ， 因为2a =，22c a =，所以1c =， 所以1b =. 所以椭圆C ：2212x y += ………………4分（II ）设A （1x ，1y ），B (2x ，2y )由直线l 与椭圆C 交于两点A ，B ，则22220y kx x y =⎧⎨+-=⎩ 所以22(12)20k x +-= ，则120x x +=，122212x x k =-+ ………………6分所以222288(1)(1)1212k AB k k k+=+=++ ………………7分 点M （2，0）到直线l 的距离221k d k=+则222221k GH r k=-+ ………………9分显然，若点H 也在线段AB 上，则由对称性可知，直线y kx =就是y 轴，矛盾，所以要使AG BH =，只要AB GH =所以222228(1)24()121k k r k k+=-++ 22424222424222(1)2(331)2(1)112231231k k k k k r k k k k k k +++=+==+++++++ ………………11分当0k =时，2r =………………12分 当0k ≠时，242112(1)2(1)31322r k k =+<+=++又显然24212(1)2132r k k =+>++, 所以23r << 综上，23r ≤< ………………14分20. 解：（Ⅰ）因为 x ∆+=3(,y x y ∆∆∆为非零整数）故1,2x y ∆=∆=或2,1x x ∆=∆=，所以点0P 的相关点有8个 ………………2分 又因为22()()5x y ∆+∆=，即221010()()5x x y y -+-=所以这些可能值对应的点在以0P 为圆心，5为半径的圆上 ………………4分（Ⅱ）依题意(,)n n n P x y 与000(,)P x y 重合则 1-12211000()()...()()n n n n n x x x x x x x x x x x --=-+-++-+-+=，1-1221100()()...()()n n n n n y y y y y y y y y y y--=-+-++-+-+= 即1-122110()+()+...+()+()=0n n n n x x x x x x x x ------，1-122110()+()+...+()+()=0n n n n y y y y y y y y ------ 两式相加得 1112-121010[()+()]+[()+()]+...+[()+()]=0n n n n n n n n x x y y x x y y x x y y -----------（*） 因为11,3(1,2,3,...,)Z i i i i i i x y x x y y i n --∈-+-==，故11()+()(=1,2,3,...,)i i i i x x y y i n ----为奇数，于是（*）的左边就是n 个奇数的和，因为奇数个奇数的和还是奇数，所以n 一定为偶数 ………………8分（Ⅲ）令11,,i i i i i i x x x y y y --∆=-∆=-(1,2,3,...,)i n =，依题意11210()()...()100n n n n y y y y y y ----+-++-=，因为0n i i T x===∑012n x x x x ++++112121(1)(1)(1)n x x x x x x =++∆++∆+∆+++∆+∆++∆ 121(1)nn n x n x x =++∆+-∆++∆………………10分 因为有3i i x y ∆∆=+，且 i i x y ∆∆，为非零整数，所以当2i x ∆=的个数越多，则 T 的值越大，而且在123,,,..,n x x x x ∆∆∆∆ 这个序列中，数字2的位置越靠前，则相应的T 的值越大 而当i y ∆取值为1或1-的次数最多时，i x ∆取2的次数才能最多，T 的值才能最大. 当 100n =时，令所有的i y ∆都为1，i x ∆都取2，则1012(12100)10201T =++++= .当100n >时，若*2(50,)n k k k =>∈N ，此时，i y ∆可取50k +个1，50k -个1-，此时i x ∆可都取2，()S n 达到最大 此时T =212((1)1)21n n n n n +++-++=++ .若*21(50,)n k k k =+≥∈N ,令2n y ∆=,其余的i y ∆中有49k -个1-，49k +个1. 相应的，对于i x ∆，有1n x ∆=,其余的都为2，则212((1)1)12T n n n n n =+++-++-=+当50100n ≤<时，令 1,2100,2,2100,i i y i n y n i n ∆=≤-∆=-<≤ 则相应的取2,2100,1,2100,i i x i n y n i n ∆=≤-∆=-<≤则T =1n ++2((1)(101))n n n +-+- ((100)(99)1)n n +-+-+ 2205100982n n +-=综上，22220510098, 50100,2(1), 100+2,100n nnT n nn n n⎧+-≤<⎪⎪⎪=+≥⎨⎪≥⎪⎪⎩且为偶数，且为奇数.………………13分。

2013年北京市各区高三一模试题汇编--立体几何一填空选择（2013年东城一模文科）（5）已知一个几何体的三视图如图所示(单位：cm)， 那么这个几何体的侧．面积是 （A）2（B）2（C）2(4 （D）2(2013年西城一模文科理科)5．某正三棱柱的三视图如图所示，其中正（主） 视图是边长为2的正方形，该正三棱柱的表 面积是（A）6 （B）12（C）12+ （D）24+(2013年西城一模文科理科)8．如图，正方体1111ABCD A BC D -中，E 是棱11B C的中点，动点P 在底面ABCD 内，且11PA A E =，则 点P 运动形成的图形是 （A ）线段 （B ）圆弧（C ）椭圆的一部分（D ）抛物线的一部分（2013年海淀一模文科）11.某几何体的三视图如图所示，则它的体积为______.（2013年海淀一模理科）8. 设为空间中三条互相平行且两两间的距离分别为4，5，6的直线.给出下列三个结论：①，使得是直角三角形； ②，使得是等边三角形；③三条直线上存在四点，使得四面体为在一个顶点处的三条棱两两互相垂直的四面体. 其中，所有正确结论的序号是123,,ll l i i A l ∃∈(1,2,3)i =123A A A ∆i i A l ∃∈(1,2,3)i =123A A A ∆(1,2,3,4)i A i =1234A A A A 侧视图A. ①B.①②C. ①③D. ②③（2013年丰台一模文科）7．某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是 (A) 2 (B) 4(C) 2(D) 4+（2013年丰台一模理科）13.某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是_______.（2013年石景山一模文科理科）7．某四棱锥的三视图如图所示，则最长的一条侧棱长度是（ ）A．B．C ．5D（2013年大兴一模文科理科）(5)已知平面βα,，直线n m ,，下列命题中不．正确的是 （A ）若α⊥m ，β⊥m ，则α∥β （B ）若m ∥n ，α⊥m ，则α⊥n （C ）若m ∥α，n =βα ，则m ∥n （D ）若α⊥m ，β⊂m ，则βα⊥．（2013年延庆一模文科理科）7.一四面体的三视图如图所示，则该四面体四个面中最大的面积是A ．2 B. 22 C ．3 D. 32（7题图）（2013年门头沟一模文科）5．如图所示，为一几何体的三视图， 则该几何体的体积是（A ）1（B ）21 （C ）13（D ）65（2013年门头沟一模理科）7．一个几何体的三视图如右图所示，则该几何体的体积是 (A) 21(B)13(C) 65 (D) 1（2013年房山一模文科）7.某三棱椎的三视图如图所示，该三棱锥的四个面的面积中，最大的是A. B. 8C.D.左视图主视图左视图俯视图二 解答题（2013年东城一模文科）（16）（本小题共14分）如图，已知AD ⊥平面ABC ，CE ⊥平面ABC ，F 为BC 的中点，若12AB AC AD CE ===．（Ⅰ）求证：//AF 平面BDE ；（Ⅱ）求证：平面BDE ⊥平面BCE ．（2013年东城一模理科）（16）（本小题共14分）如图，已知ACDE 是直角梯形，且//ED AC ，平面ACDE ⊥平面ABC ，90BAC ACD ∠=∠=︒，AB AC AE ==2=，12ED AB =， P 是BC 的中点． （Ⅰ）求证：//DP 平面EAB ；（Ⅱ）求平面EBD 与平面ABC 所成锐二面角大小的余弦值．(2013年西城一模文科)16．（本小题满分14分）在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD，AC =22AB BC ==，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ； （Ⅱ）求四面体FBCD 的体积；（Ⅲ）线段AC 上是否存在点M ，使EA //平面FDM ？ 证明你的结论．A BCDEF(2013年西城一模理科)17．（本小题满分14分）在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD ，BC AB 2=，60ABC ︒∠=，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ；（Ⅱ）求BC 与平面EAC 所成角的正弦值；（Ⅲ）线段ED 上是否存在点Q ，使平面EAC ⊥平面QBC ？ 证明你的结论．（2013年海淀一模文科）17. （本小题满分14分）在四棱锥P ABCD -中，PA ⊥平面ABCD ，ABC ∆是正三角形，AC 与BD 的交点M 恰好是AC 中点，又30CAD ∠=，4PA AB ==，点N 在线段PB 上，且13PN NB =． （Ⅰ）求证：BD PC ⊥；（Ⅱ）求证：//MN 平面PDC ；（Ⅲ）设平面PAB 平面PCD =l ，试问直线l 是否与直线CD 平行，请说明理由.（2013年海淀一模理科）17.（本小题满分14分）在四棱锥中，平面，是正三角形，与的交点恰好是中点，又，，点在线段上，且（Ⅰ）求证：； （Ⅱ）求证：平面; （Ⅲ）求二面角的余弦值．P ABCD -PA ⊥ABCD ABC ∆AC BD M AC 4PA AB ==120CDA ∠=N PB PN =BD PC ⊥//MN PDC A PC B --（2013年丰台一模文科）16． 如图，四棱锥P -ABCD 中， BC ∥AD ，BC =1，AD =3，AC ⊥CD ,且平面PCD ⊥平面ABCD . （Ⅰ）求证：AC ⊥PD ；（Ⅱ）在线段PA 上,是否存在点E ，使BE ∥平面PCD ？若存在，（2013年丰台一模理科）16．如图，四边形ABCD 是边长为2的正方形，MD ⊥平面ABCD ，NB ∥MD ，且NB=1，MD=2；（Ⅰ）求证：AM ∥平面BCN; （Ⅱ）求AN 与平面MNC 所成角的正弦值；（Ⅲ）E 为直线MN 上一点，且平面ADE ⊥平面MNC ，求ME MN的值.（2013年石景山一模文科）17．（本小题满分14分）如图，在底面为直角梯形的四棱锥P －ABCD 中，AD ∥BC ，∠ABC=90o ，PD ⊥平面ABCD ，AD =1，BC =4。