八年级数学上学期第14周周练试卷(含解析) 苏科版 (2)

周滚动练(14.2~14.3)(时间:45分钟满分:100分)一、选择题(每小题4分,共32分)1.下列各式由左到右的变形中,属于分解因式的是(C)A.a(m+n)=am+anB.a2-b2-c2=(a-b)(a+b)-c2C.10x2-5x=5x(2x-1)D.x2-16+6x=(x+4)(x-4)+6x2.多项式x2-1与多项式x2-2x+1的公因式是(A)A.x-1B.x+1C.x2-1D.(x-1)23.下列多项式中,能用平方差公式分解因式的是(A)A.-x2+16B.x2+9C.-x2-4D.x2-2y4.已知x2+kx+4可以用完全平方公式进行因式分解,则k的值为(D)A.-4B.2C.4D.±45.下列关于962的计算方法正确的是(D)A.962=(100-4)2=1002-42=9984B.962=(95+1)(95-1)=952-1=9024C.962=(90+6)2=902+62=8136D.962=(100-4)2=1002-2×4×100+42=92166.已知a+b=3,ab=2,则(a2+b2)2的值为(C)A.9B.16C.25D.367.已知a,b,c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC一定是(C)A.锐角三角形B.钝角三角形C.等腰三角形D.等边三角形8.如图,长方形ABCD 的周长为16,以长方形的四条边为边长向外作四个正方形,若四个正方形的面积之和为68,则长方形ABCD 的面积为( B )A.12 B .15 C .18 D .20二、填空题(每小题4分,共20分)9.已知xy=2,x+y=3,则x 2y+xy 2= 6 .10.若把多项式x 2+ax+b 分解因式的结果为(x+1)·(x-2),则a+b 的值为 -3 . 11.边长为a ,b 的长方形,它的周长为14,面积为10,则a 2b+ab 2的值为 70 .12.已知a-1a=2,则a 2+1a2= 6 .13.已知a 2+a-3=0,则a 3+3a 2-a+4的值为 10 . 三、解答题(共48分) 14.(9分)分解因式: (1)2x 2-8;解：原式=2(x+2)(x-2). (2)m 3n-10m 2n+25mn ;解：原式=mn(m-5)2 (3)a 2(a-b )+9(b-a ).解：原式=(a-b)(a+3)(a-3)15.(5分)已知a+b=3,ab=2,求代数式a 3b+2a 2b 2+ab 3的值.解：a 3b+2a 2b 2+ab 3=ab(a 2+2ab+b 2)=ab(a+b)2，将a+b=3，ab=2代入,得ab(a+b)2=2×32=18.16.(8分)利用乘法公式有时能进行简便计算. 例:101×99=(100+1)(100-1)=1002-12=10000-1=9999.请参考给出的例题,通过简便方法计算: (1)2002×1998;(2)86×3.14+34×3.14-20×3.14..解：(1)2002×1998＝(2000+2)(2000-2)＝20002-22＝3999996.(2)86×3.14+34×3.14-20×3.14＝3.14×(86+34-20)＝3.14×100＝314.17.(8分)用四个长为m、宽为n的相同长方形按如图方式拼成一个正方形.(1)根据图形写出一个代数恒等式: (m-n)2＝(m+n)2-4mn.;(2)已知3m+n=9,mn=6,试求3m-n的值.解(2)∵(3m-n)2＝(3m+n)2-12mn，∴(3m-n)2＝81-72＝9,∴3m-n=318.(8分)在x4-2x2y2-y4,x4+y4,2x2y2这三个整式中,取其中的两个进行和或差的运算,使得计算后所得的多项式分别满足相应的要求并解答.(1)该多项式因式分解时,只运用了平方差公式;(2)该多项式因式分解时,只运用了完全平方公式;(3)该多项式因式分解时,既运用了平方差公式,又运用了完全平方公式.解：(1)x4-2x2y2-y4+2x2y2=x4-y4=(x2+y2)(x+y)(x-y).(2)x4+y4+2x2y2=(x2+y2)2.(3)x4+y4-2x2y2=(x2-y2)2=(x+y)2(x-y)2.19.(10分)(1)填空:(a-b)(a+b)=a2-b2;(a-b)(a2+ab+b2)=a3-b3;(a-b)(a3+a2b+ab2+b3)= a4-b4.(2)猜想:(a-b)(a n-1+a n-2b+…+ab n-2+b n-1)=an-bn(其中n为正整数,且n≥2).(3)利用(2)猜想的结论计算:29-28+27-…+23-22+2.令S=29-28+27-…+23-22+2,∴S-1=29-28+27-…+23-22+2-1=［2-(-1)］(29-28+27-…+23-22+2-1)×13 =341.=(210-1)×13∴结果应为342.。

八年级数学(上)周周练(1.1～1.3)（满分：100分时间：90分钟）一、选择题(每小题2分，共20分)1．下列图案中，是轴对称图形的是( )2．下列四幅图案中，不是轴对称图形的是( )3．下列图案中，是轴对称图形的有( )A．1个B．2个C．3个D．4个4．下列轴对称图形中，对称轴最多的是( )5．如图是小华在镜子中看到的身后墙上的钟，你认为实际时问最接近8点的是( )6．把一个图形先沿着一条直线进行轴对称变换。

再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换．在自然界和日常生活中，大量地存在这种图形变换(如图①)．结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换过程中，两个对应三角形(如图②)的对应点所具有的性质是( )A．对应点连线与对称轴垂直B．对应点连线被对称轴平分C．对应点连线被对称轴垂直平分D．对应点连线互相平行7．如图，把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点把平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )A．正三角形B．正方形C．正五边形D．正六边形8．下列语句：①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③一个轴对称图形不一定只有一条对称轴；④两个轴对称图形的对应点一定在对称轴的两侧，其中正确的是( )A．①B．①③C．①②③D．①③④9．剪纸是中国的民间艺术，剪纸的方法很多，如图是一种剪纸方法的图示，先将纸折叠，然后再剪，展开即得到图案，则下列的四个图案中，不能用上述方法剪出的是( )10．如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴，若∠AFC+∠BCF=150°，则∠AFE+OBCD的度数为( )A．150°B．300°C．210°D．330°二、填空题(每小题2分，共16分)11．长方形有______条对称轴，正方形有_______条对称轴，圆有______条对称轴．12．在缩写符号SOS、CCTV、BBC、WWW、TNT中，成轴对称图形的是___________．13．计算器上显示的0～9这十个数字中，是轴对称图形的是__________．14．如图，把图中某两个小方格涂上阴影，使整个图形是以虚线为对称轴的轴对称图形．第14题第15题第16题15．星期天小华去书店买书时，从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示，此时时钟表示的时间是___________________(按12小时制填写)．16．张军是学校足球队的运动员，他在镜子里看到衣服上的号码如图所示，则他是________号运动员．17．如图，桌面上有A、B两个球，若要将B球射向桌面任意一边，使一次反弹后击中A 球，则图中的8个点中，可以瞄准的点有__________个．第17题第18题18．如图，直线l是四边形ABCD的对称轴．若AD∥BC，则下列结论：①AB∥CD；②AB=BC；③A B⊥BC；④AO=OC，其中正确的是____________________(填序号)．三、耐心解一解(共64分)19．(10分)在下列图形中找出轴对称图形，并找出它的两组对应点．20．(8分)已知点A和点B关于某条直线对称，请你画出这条直线．21．(8分)如图是方格纸中画出的树形的一半，请你以树干为对称轴画出图形的另一半．22．(12分)如图是由两个等边三角形组成的图形，它是轴对称图形吗?如果不是，可以移动其中一个三角形，使它与另一个三角形一起组成轴对称图形，那么怎样移动才能使所构成的图形具有尽可能多的对称轴?23．(13分)如图，A是锐角∠MON内的一点，试分别在OM、ON上确定点B、C，使△ABC的周长最小．写出你作图的主要步骤，并标明你所确定的点(要求画出草图，保留作图痕迹)．24．(13分)某居民小区搞绿化，要在一块矩形空地上铺草坪，现征集设计方案，要使设计的图案由圆或正方形组成(圆和正方形的个数、大小不限)，并且使整个矩形场地成轴对称图形，请在矩形中画出你设计的方案．参考答案—、1．C 2．A 3．C 4．A 5．D 6．B 7．D 8．B 9．D 10．B二、11．2 4 无数12．BBC、WWW 13．0、1、3、8 14．如图所示15．下午1：30 16．16 17．2 18．①②④三、19．①、②、③、⑤都是轴对称图形，对应点略20．图略连接AB，作出线段AB 的垂直平分线l，即为它们的对称轴21．如图所示22．不是轴对称图形．将小的等边三角形移动到大的等边三角形内部图略23．分别作点A关于OM、ON的对称点A′、A″，连接A′A″，分别交OM、ON于点B、C，连接AB、AC．则点B、C即为所求．如图所示24．答案不唯一，如图所示。

A. B. C. D.苏教版初中数学八年级上册第一学期第14周周考试卷姓名： 班级： 得分：一、选择题（每小题3分，共27分）1．在平面直角坐标系中，点A （2，-3）在第（ ）象限．A ．一；B ．二；C ．三；D ．四；2．坐标平面上有一点A ，且A 点到x 轴的距离为3，A 点到y 轴的距离恰为到x 轴距离的3倍．若A 点在第二象限，则A 点坐标为何？（ ）A ．（-9，3）；B ．（-3，1）；C ．（-3，9）；D ．（-1，3）；3.已知点P ()1,23a a +-关于x 轴的对称点在第一象限，则a 的取值范围是（ ）A ．312a -<<；B ．312a -<<；C ．1a <-；D ．32a >； 4.将点A （3，2）沿x 轴向左平移4个单位长度得到点A ′，点A ′关于y 轴对称的点的坐标是（ ）A ．（-3，2）；B ．（-1，2）；C ．（1，2）；D ．（1，-2）；5.在平面直角坐标系中，将点P （-2，1）向右平移3个单位长度，再向上平移4个单位长度得到点P ′的坐标是（ ）A ．（2，4）；B ．（1，5）；C ．（1，-3）；D ．（-5，5）；6.若点A ()2,n -在x 轴上，则点B ()1,1n n -+在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7.在平面直角坐标系内，点P （-2，3）关于原点的对称点Q 的坐标为（ ）A ．（2，-3）；B ．（2，3）；C ．（3，-2）；D ．（-2，-3）；8.已知点M ()12,1m m --关于x 轴的对称点在第一象限，则m 的取值范围在数轴上表示正确的是（ ）9.点N (),x y 在x 轴下方、y 轴左侧，且30x -=，240y -=，则点N 的坐标为（ ）A.（-3，-2）；B. （-3，2）；C.（3，-2）；D.（3，2）；二、填空题（每小题3分，共21分）10. 坐标系中，已知点A ()2,8a b --与点B ()2,3a b -+关于原点对称，则a = b = ．11.已知点M （3，-2），将它先向左平移4个单位，再向上平移3个单位后得到点N ，则点N 的坐标是 ．12．如图，若在象棋盘上建立直角坐标系，使“帅”位于点（-1，-2）．“馬”位于点（2，-2），则“兵”位于点 .第16题图第15题图13.在平面直角坐标系中，点P (),2m m -在第一象限内，则m 的取值范围是 ．14.已知点P ()25,1m m --，则当m = 时，点P 在第一、三象限的角平分线上.15.如图，A 、B 的坐标分别为（1，0）、（0，2），若将线段AB 平移到至11A B ，1A 、1B 的坐标分别为()2,a 、(),3b ，则a b += ．16．将等腰直角三角形AOB 按如图所示放置，然后绕点O 逆时针旋转90°至△A ′OB ′的位置，点B 的横坐标为2，则点A ′的坐标为 .三、解答题（共52分）17.（本题满分10分）如图，在直角坐标系中，Rt △AOB 的两条直角边OA ，OB 分别在x 轴的负半轴，y 轴的负半轴上，且OA=2，OB=1．将Rt △AOB 绕点O 按顺时针方向旋转90°，再把所得的像沿x 轴正方向平移1个单位，得△CDO ．（1）写出点A ，C 的坐标；（2）求点A 和点C 之间的距离．18.（本题满分10分）如图，在方格纸中（小正方形的边长为1），△ABC 的三个顶点均为格点，将△ABC 沿x 轴向左平移5个单位长度，根据所给的直角坐标系（O 是坐标原点），解答下列问题：（1）画出平移后的△A ′B ′C ′，并直接写出点A ′、B ′、C ′的坐标；（2）求出在整个平移过程中，△ABC 扫过的面积．19.（本题满分10分）在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三角形叫做“格点三角形”根据图形，解决下面的问题：（1）图中的格点△A′B′C′是由格点△ABC通过哪些变换方法得到的？（2）如果以直线a，b为坐标轴建立平面直角坐标系后，点A的坐标为（-3，4），请写出格点△DEF各顶点坐标，并求出△DEF的面积．20.（本题满分11分）在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（-4，5），（-1，3）．（1）请在如图所示的网格平面内作出平面直角坐标系；（2）请作出△ABC关于y轴对称的△A′B′C′；（3）点B′的坐标为．（4）△ABC的面积为．21.（本题满分11分）如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．。

卜人入州八九几市潮王学校灌云县四队二零二零—二零二壹八年级数学上学期第14周周练试题选择题〔4分×7题=28分〕1．〔2021.〕在平面直角坐标系中，点A 〔2，-3〕在第〔〕象限．A ．一；B ．二；C ．三；D ．四；2.以下各式中，正确的选项是〔〕2=-；9=；3=±；13=；3.以下各数中，互为相反数的一组是〔〕A.-2B.-2；C.-2与12-；D.2-与2； 鲸的体重约为51.3610⨯㎏，关于这个近似数，以下说法正确的选项是〔〕A ．它准确到百位；B ．它准确到0.01；C ．它准确到千分位；D ．它准确到千位；5.一直角三角形的两边长分别为3和4，那么第三边的长为〔〕A ．5；B ；CD ．5；6．〔2021•HY 〕坐标平面上有一点A ，且A 点到x 轴的间隔为3，A 点到y 轴的间隔恰为到x 轴间隔的3倍．假设A 点在第二象限，那么A 点坐标为何？〔〕A ．〔-9，3〕；B ．〔-3，1〕；C ．〔-3，9〕；D ．〔-1，3〕；7.〔2021•〕点P()1,23a a +-关于x 轴的对称点在第一象限，那么a 的取值范围是〔〕 A ．312a -<<； B ．312a -<<；C ．1a <-； D ．32a >； 填空题〔4分×7空=28分〕6的平方根是的算术平方根是.22m n x y --与423m n x y +是同类项，那么3m n -的立方根是.11.假设13a b <<，且a 、b 为连续正整数，那么22b a -=.12.〔2021•〕如图，正方形ODBC 中，OC=1，OA=OB ，那么数轴上点A 表示的数是．13.〔2021.〕点M 〔3，-2〕，将它先向左平移4个单位，再向上平移3个单位后得到点N ，那么点N 的坐标是． 计算题〔4分×5空=20分〕14.求以下各式的值：〔1〕196x 2=〔2〕010-x 52=〔3〕135-3-x 2252=）（〔4〕1251-x 3=）（作图题〔15题5分〕5-的点.提升题〔16题6分，17题〔1〕6分，〔2〕7分〕实数a b ，互为相反数，c d ，互为倒数，6x =，求代数式()223x a b cd x a b cd ++++++的值. 17.〔1〕3x y -+与1x y +-互为相反数，求()2x y -的平方根. 〔2〕24248y x x =-+--，求35x y -的值. 第12题图。

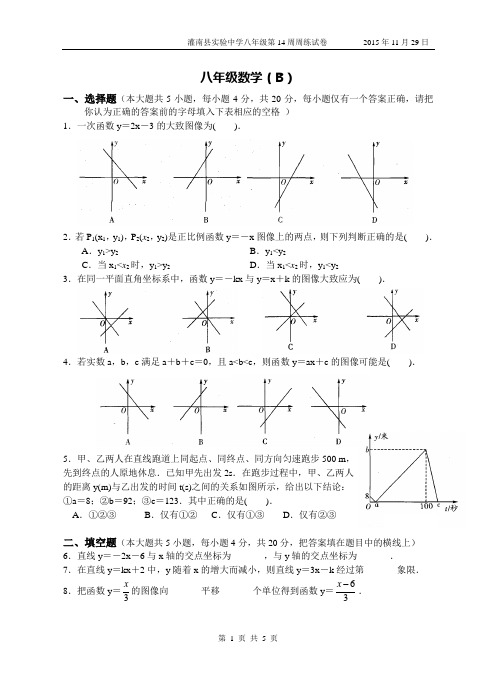
八年级数学（B）一、选择题（本大题共5小题，每小题4分，共20分，每小题仅有一个答案正确，请把你认为正确的答案前的字母填入下表相应的空格）1．一次函数y＝2x－3的大致图像为( )．2．若P1(x1，y1)，P2(x2，y2)是正比例函数y＝－x图像上的两点，则下列判断正确的是( )．A．y1>y2B．y1<y2C．当x1<x2时，y1>y2D．当x1<x2时，y1<y23．在同一平面直角坐标系中，函数y＝－kx与y＝x＋k的图像大致应为( )．4．若实数a，b，c满足a＋b＋c＝0，且a<b<c，则函数y＝ax＋c的图像可能是( )．5．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m，先到终点的人原地休息．已知甲先出发2s．在跑步过程中，甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示，给出以下结论：①a＝8；②b＝92；③c＝123．其中正确的是( )．A．①②③B．仅有①②C．仅有①③D．仅有②③二、填空题（本大题共5小题，每小题4分，共20分，把答案填在题目中的横线上）6．直线y＝－2x－6与x轴的交点坐标为_______，与y轴的交点坐标为_______．7．在直线y＝kx＋2中，y随着x的增大而减小，则直线y＝3x－k经过第_______象限．8．把函数y＝3x的图像向_______平移_______个单位得到函数y＝63x．9．如图，一次函数y＝kx＋b的图像与正比例函数y＝2x的图像平行且经过点A（1，－2），则kb＝_______．10. 某地长途汽车客运公司规定每位旅客可随身携带一定的行李，如果超出规定，那么需要购买行李票，行李票y(元)是行李质量x(kg)的一次函数，其图像如图．则每位旅客最多可免费携带千克行李．三、解答题（本大题共6小题，共60分，解答应写出必要的文字说明、证明过程或演算步骤）11．（本题9分）已知直线y＝kx＋b经过点A(0，6)，B(3，0)．(1)求出这条直线的函数关系式；(2)若这条直线经过点P(m，2)，求m的值；(3)求这条直线与两坐标轴所围成的三角形的面积．12．（本题9分）已知一次函数y＝(1－a)x＋4a－1的图像．(1)经过原点，求a；(2)与直线y＝2x平行，求a；(3)与y轴交于正半轴，且y随x的增大而增大，求a的取值范围．13. （本题10分）某厂家生产两种款式的布质环保购物袋，每天共生产4500个，两种购物袋的成本和售价如下表，设每天生产A种购物袋x个，每天共获利y元．(1)求y与x的函数关系式；(2)如果该厂每天最多投入成本10000元，那么每天最多获利多少元？14．（本题10分）灌南至新浦高速公路的路基工程分段招标，市路桥公司中标承包了一段路基工程，进入施工场地后，所挖筑路基的长度y(m)与挖筑时间x（天）之间的函数关系如图所示，请根据提供的信息解答下列问题：(1)请你求出：①在0≤x<2的时间段内，y与x的函数关系式；②在x≥2的时间段内，y与x的函数关系式．(2)用所求的函数解析式预测完成1620 m的路基工程需要挖筑多少天？15．（本题10分）甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向体育馆．图是甲、乙两人在跑步的全过程中经过的路程y（米）与甲出发的时间x(秒)的函数图像．(1)在跑步的全过程中，甲共跑了_______米，甲的速度为_______米／秒；(2)乙跑步的速度是多少？乙在途中等候甲用了多长时间？(3)甲出发多长时间第一次与乙相遇？此时乙跑了多少米？16．（本题12分）如图(1)，A、B、C为三个超市，在A通往C的道路（粗实线部分）上有一点D，D与B有道路（细实线部分）相通．A与D，D与C，D与B之间的路程分别为25 km，10 km，5 km现计划在A通往C的道路上建一个配货中心H，每天有一辆货车只为这三个超市送货．该货车每天从H出发，单独为A送货1次，为B送货1次，为C送货2次．货车每次仅能给一家超市送货，每次送货后均返回配货中心H，设H到A的路程为x km，这辆货车每天行驶的路程为y km(1)用含x的代数式填空：当0≤x≤25时，货车从H到A往返1次的路程为2x km，货车从H到B往返1次的路程为_______km，货车从H到C往返2次的路程为_______km，这辆货车每天行驶的路程y＝_______．当25<x≤35时，这辆货车每天行驶的路程y＝_______；(2)请在图(2)中画出y与x(0≤x≤35)的函数图像；(3)配货中心H建在哪段，这辆货车每天行驶的路程最短？。

苏科版八年级数学上册勾股定理单元测试卷14一、选择题（共10小题；共50分）1. 下列各组数中不能作为直角三角形的三边长的一组是A. ，，B. ，，C. ，，D. ，，2. 若一个三角形的三边长的平方分别为，，，则使此三角形是直角三角形的的值是A. B. C. D. 或3. 下列各组数中，能构成直角三角形的是A. ，，B. ，，C. ，，D. ，，4. 我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”．如图，由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形，正方形，正方形的面积分别为，，，若，则的值是A. B. C. D.5. 甲、乙两艘客轮沿不同方向同时离开港口，航行的速度都是，甲客轮到达点，乙客轮用到达点，若，两点的直线距离为，甲客轮沿北偏东的方向航行，则乙客轮的航行方向可能是A. 南偏西B. 北偏西C. 南偏东D. 南偏西6. 以下列三个正数为三边长度，能构成直角三角形的是A. ，，B. ，，C. ，，D. ，，7. 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若，，则该矩形的面积为A. B.8. 如果正整数，，满足等式，那么正整数，，叫做勾股数．某同学将自探究勾股数的过程列成下表，观察表中每列数的规律，可知的值为A. B. C. D.9. 如图，在中，，是的中点，，交的延长线于点．若，，则的长为A. C. D.10. 下列说法正确的是A. 若，，是的三边，则B. 若，，是的三边，则C. 若，，是的三边，，则D. 若，，是的三边，，则二、填空题（共6小题；共30分）11. 已知三角形的三边长分别为厘米、厘米、厘米，那么这个三角形是．12. 如图，已知，且，，，则的长是．13. 已知一个三角形的三条边的长分别为，和，那么这个三角形的最大内角的大小为度．14. 图 1 是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若，，将四个直角三角形中边长为的直角边分别向外延长一倍，得到如图2 所示的"数学风车"，则这个风车的外围周长是．15. 三角形的三边长分别为，，，则这个三角形的面积是．16. 如图中，，垂足为，若，，，则的长是 .三、解答题（共8小题；共104分）17. 如图，已知，，，．求证：是的中点．18. 如图，，垂足为，，，．求证：．19. 如图，已知三角形一条边长为，这条边上的中线的长为，另两边之和是，求这个三角形的面积．20. 如图，在中，，，点在上，且，．（1）求证：．（2）求的长．21. 在中，，，，求的长．22. 已知：如图，四边形中，，，，，．试判断的形状，并说明理由．23. 小明将一副三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长，若已知，求的长．24. 如图，在正方形中，是的中点，是上一点，且．求证．答案第一部分1. A2. D3. B4. D5. C【解析】如图：甲乙两艘客轮同时离开港口，航行的速度都是每分钟，甲客轮用分钟到达点，乙客轮用分钟到达点，甲客轮走了，乙客轮走了，，两点的直线距离为，，，甲客轮沿着北偏东的方向航行，乙客轮的航行方向可能是南偏东．故选C．6. A7. B8. C 【解析】由题可得，，，，，，，当时，，，，，故选：C．9. A 【解析】，，，是的中点，．由题意可得：两式相减得：，解得，．10. D第二部分11. 直角三角形12.13.【解析】，三角形为直角三角形，这个三角形的最大内角度数为．14.【解析】在中，．所以风车外围周长为．15.【解析】因为三角形的三边长分别为，，，所以，所以此三角形为直角三角形，所以这个三角形的面积．16.第三部分17. 提示：连接，，证．18. ，，．，，，．，，是直角三角形，且．19. 如图，由，可得，，从而有，．，．．．．即面积为．20. （1）在中，，，，，，，是直角三角形，且，．（2）由（）知，，，，，在中，，，的长为．21. ．22. ，，，，，，，是直角三角形．23. ，，设，则，，，，，，．24. 设，则，，，，，同理，，，，根据勾股定理的逆定理，为直角三角形．．。

第十五章 分式测试题（总分120分，时间60分钟）姓名： 成绩：一、选择题（每小题3分，共30分）1、在式子：23123510,,,,,94678xy a b c x y x a x y π+++中，分式的个数是( ) A ：2 B ：3 C ：4 D ：52、化简1x x y x ÷⋅的结果是（ ）A ：1 B ：xy C ：y x D ：x y 3、若把分式xy x 23+的x 、y 同时扩大10倍，则分式的值（ ） A ：扩大10倍B ：缩小10倍C ：不变D ：缩小5倍 4、化简2293m m m --的结果是（ ） A ：3+m m B ：3+-m m C ：3-m m D ：m m -3 5、对于分式23x -有意义，则x 应满足的条件是（ ） A ：3x ≥ B ：3x > C ：3x ≠ D ：3x < 6、用科学记数法表示-0.0000064记为（ ）A ：-64×10-7B ：-0.64×10-4C ：-6.4×10-6D ：-640×10-87、若分式112--x x 的值为0，则x 的取值为（ ）A ：1=x B ：1-=x C ：1±=x D ：无法确定 8、下列等式成立的是（ ）A ：9)3(2-=-- B ：()9132=-- C ：2222b a b a ⨯=⨯-- D ：b a a b b a +=--22 9、若方程342(2)a x x x x =+--有增根，则增根可能为（ ）A ：0 B ：2 C ：0或2 D ：1 10、小明和小张两人练习电脑打字，小明每分钟比小张少打6个字，小明打120个字所用的时间和小张打180个字所用的时间相等。

设小明打字速度为x 个/分钟，则列方程正确的是（ ）A ：x x 1806120=+B ：x x 1806120=-C ：6180120+=x xD ：6180120-=x x 二、填空题（每小题3分，共30分） 11、计算：=-321)(b a ；=+-203π ； 12、方程xx 527=-的解是 ； 13、分式,21x xy y 51,212-的最简公分母为 ； 14、约分：=-2264xy y x ；932--x x = ； 15、若关于x 的方程211=--ax a x 的解是x=2，则a= ； 16、计算ab b b a a -+-＝ ； 17、如果分式121+-x x 的值为－1，则x 的值是 ； 18、已知31=b a ，分式ba b a 52-+的值为 ； 19、当x 时，分式21x x -的值为正数； 20、轮船顺水航行46km 和逆水航行34km 所用的时间恰好相等，水的流速是3km/h ，设轮船在静水中的速度是xkm/h ，可列得方程为 。

初中数学试卷宜兴外国语学校初二数学第十四周周测试卷班级 姓名 成绩 签字 一．选择（每题5分，共20分）1. 有下列函数：①y ＝2x ；②y ＝－x －100；③y ＝2－3x ；④y ＝x 2－1．其中是一次函数的有 A ．1个 B ．2 C ．3个 D ．4个 ( )2．若函数是一次函数，则应满足的条件是 ( )A.且B.且C.且 D.且 3.已知一次函数，当增加3时，减少2，则的值是 ( )A.32-B.23-C.32D.23 4．已知函数y ＝kx ＋b ，当x=-1时y=-2；x=-2时y=0，则不等式2x<kx ＋b<0的解集为 ( )A ．x<－2B ．－2<x< －1C ．－2<x<0D ．－1<x<0二．填空（每题5分，共25分）5．在函数y ＝ 中，自变量x 的取值范围是_______． 6.已知函数y ＝(k －2)x ＋2k+1，当k ＝_______时，它是正比例函数．7. 若函数()1232+++=-a x a y a 是一次函数，则 a= 。

8．已知梯形的面积是6，高是4，则梯形的上底y 关于下底x 的函数关系式是_______．9.某书定价20元，如果一次购买25本以上，超过25本的部分打七五折，试写出付款金额y （单位：元）与购书数量x （单位：本）之间的函数关系_____________________三．解答题10. （8分）已知y+2与2x+12成正比例，且x=3时y=5(1) 求y 与x 之间的函数关系式； (2) 当y =1时，求x 的值.11. （10分）在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系．下面是蟋蟀所叫次数与温度变化情况对照表：蟋蟀叫次数 … 84 98 119 …温度（℃） … 15 17 20 …（1）根据表中数据确定该一次函数的关系式；（2）如果蟋蟀1分钟叫了63次，那么该地当时的温度大约为多少摄氏度？62-x x12. （10分）某商场欲购进A 、B两种品牌的饮料共500箱，此两种饮料每箱的进价和售价如下表所示。

八年级上数学周末作业（第14周）一、选择题（每题2分，共22分） 班级_________姓名________1. 已知点在轴上，则点的坐标是A ．B ．C ．D ．2. 如果点在第二象限，那么点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限3. 下列各图中能说明y 是x 的函数的是（ ）A ．B ．C ．D ．4. 在平面直角坐标系中，将直线l 1：y ＝3x +3平移得到的直线l 2：y ＝3x ﹣9，则下列平移方式叙述错误的是（ ）A ．将l 1向下平移12个单位长度得到l 2B ．将l 1向右平移2个单位长度，再向下平移6个单位长度得到l 2C ．将l 1向右平移4个单位长度得到l 2D ．将l 1向右平移3个单位长度，再向下平移2个单位长度得到l 25. 若点A （a +1，a ﹣2）在第二、四象限的角平分线上，则点B （﹣a ，1﹣a ）在（ ）A ．第一象限B ．第二象限C ．第三象跟D ．第四象限6. 函数y ＝3-2-x x 的自变量x 的取值范围是（ ） A ．x ≥2B ．x ≠3且x ≠﹣3C ．x ≥2且x ≠3D ．x ≥2且x ≠﹣3 7. 如果，且不等式解集是，那么函数的图象只可能是下列的A ．B ．C ．D ． 8. 一次函数沿轴平移3个单位得直线与，则的值为 (2,24)P m m +-x P ()(4,0)(0,4)(4,0)-(0,4)-(2,)P a b -(2,)Q a b -+()0kb <0kx b +>b x k<-y kx b =+()43y x b =-y 413y x =-b ()A ．或4B ．2或C ．4或D ．或69. 两条直线y 1＝ax ﹣b 与y 2＝bx ﹣a 在同一坐标系中的图象可能是图中的（ ）A ．B ．C ．D ．10. 在平面直角坐标系中，点A （a ，0），点B （2﹣a ，0）,且A 在B 的左边，点C （1，﹣1），连接AC ，BC ，若在AB ，BC ，AC 所围成区域内（含边界），横坐标和纵坐标都为整数的点的个数为4个，那么a 的取值范围为（ ）A ．﹣1＜a ≤0B ．0≤a ＜1C ．﹣1＜a ＜1D ．﹣2＜a ＜211. 在平面直角坐标系中，一个智能机器人接到的指令是：从原点出发，按“向上向右向下向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点，第二次移动到点第次移动到点，则点的坐标是A ．B ．C ．D ．二、填空题（每题2分，共22分）12. 若点在第一、三象限的角平分线上，且点到轴的距离为2，则点的坐标是 ．13. 函数321y x x =--中自变量x 的取值范围是 ． 14. 比较：√3−1______√32.15. 已知线段，轴，若点坐标为，则点的坐标为 ．16. 已知直线y ＝（2﹣3m ）x 经过点A （x 1，y 1）、B （x 2，y 2），当x 1＜x 2时，有y 1＞y 2，则m 的取值范围是 ．17.若一次函数y ＝（1﹣2m ）x +3﹣2m 的图象不经过第三象限，则m 的取值范围是 ．18. 在平面直角坐标系中，对于平面内任意一点（a ，b ），若规定以下三种变换： 2-4-6-4-O →→→1A 2A ⋯⋯n n A 2019A ()(1010,0)(1010,1)(1009,0)(1009,1)N N y N 5MN =//MN y M (1,2)-N①f （a ，b ）＝（﹣a ，b ），如f （1，3）＝（﹣1，3）①g （a ，b ）＝（b ，a ），如g （1，3）＝（3，1）①h （a ，b ）＝（﹣a ，﹣b ），如h （1，3）＝（﹣1，﹣3）按照以上变换有f [g （2，3）]＝f （3，2）＝（﹣3，2）那么g [h （5，1）]＝ . 19. 已知一次函数的图象经过点P （﹣3，0），且与两坐标轴截得的三角形面积为4，则此一次函数的解析式为 ．20. 如图，已知函数y 1＝ax +b 和y 2＝kx 的图象交于点P ，则根据图象可得，方程ax +b ﹣kx ＝0的解是 ．21. 已知，，若规定，则的最小值为 ．22. 将函数为常数）的图象位于轴下方的部分沿轴翻折至其上方后，所得的折线是函数为常数）的图象．若该图象在直线下方的点的横坐标满足，则的取值范围为 ．三、解答题（共56分）23.计算（8分）（1）()2-0)21(-2019-2-312π++ （2）2-41278-2-13×+24.（8分）求下列各式中的x.（1）4（3x +1）2﹣1＝0 （2）8x 3+27＝0 1m x =+2n x =-+1,1,m n m n y m n m n +-⎧=⎨-+<⎩y 3(y x b b =+x x |3|(y x b b =+3y =x 05x <<b25. （6分）已知y -2与x+1成正比例函数关系，且当x=-2时，y =6.（1）求出y 与x 之间的函数表达式；（2）求此函数的图像与坐标轴的交点的坐标.26.（6分）已知A =√m +3m−4是m +3的算术平方根B =√n −22m−4n+3是n ﹣2的立方根,试求：（1）m 和n 的值；（2）A ﹣B 的值．27.（8分）操作发现（1）如图，在平面直角坐标系中有一点，将点先向右平移3个单位长度，再向下平移3个单位长度得到点，则点的坐标为 ；并在图中面出直线的函数图象.（2）直接写出直线的解析式 .（3）若直线上有一动点，设点的横坐标为①直接写出点的坐标 .②若点位于第四象限，直接写出三角形的面积 .（用含的式子表示）28. （10分）已知一次函数y ＝（2m +3）x +m ﹣1，（1）若函数图象经过原点，求m 的值；（2）若函数图象在y 轴上的截距为﹣3，求m 的值；（3）若函数图象平行于直线y ＝x +1，求m 的值；（4）若该函数的值y 随自变量x 的增大而减小，求m 的取值范围；（5）该函数图象不经过第二象限，求m 的取值范围．(2,3)A A B B AB AB AB P P t P P BOP t29.（10分）点P（x，y）在第一象限,且x+y＝8,点A的坐标为（6,0），设△OP A的面积为S．（1）用含x的式子表示S，写出x的取值范围；（2）当点P的横坐标为5时，△OP A的面积为多少？（3）当S＝12时，求点P的坐标；（4）△OP A的面积能大于24吗？为什么？。

初二数学周练(第14周)一、选择题（本大题共8小题，每小题3分，共24分）1．一只小虫从点A （-2,1）出发，先向右跳4个单位长度，再向下跳3个单位长度，到达点B 处，则点B 的坐标是（ ）A. (5,5)-B. (2,2)-C. (1,5)D. (2,2)2．如桌点(3,24)P m m ++在y 轴上，那么点P 的坐标为（ ）A. (2,0)-B. (0,2)-C. (1,0)D. (0,1)3．下列各式中，正确的是（ ）A ．＝±2B ．＝3C ．＝﹣3D ．＝﹣3 4．点（1，﹣3）关于y 轴对称点的坐标是（ ）A ．（﹣1，﹣3）B ．（﹣3，1）C ．（﹣1，3）D ．（1，3）5．如图，在△ABC 和△DEF 中，AC =DF ，AB =DE ，添加下列一个条件后，仍然不能证明△ABC ≌△DEF ，这个条件是（ ）A ．∠A =∠DB ．∠B =∠DEFC ．∠ACB =∠DFE =90°D ．BE =CF6．如图，在∠ A OB 的两边上，分别取OM = ON ，再分别过点 M 、 N 作OA 、OB 的垂线， 交点为 P ，画射线OP ，则OP 平分∠ AOB 的依据是（ ）A ． S ASB ． SSSC ． H LD ． A AS第5题 第6题 第8题7．在平面直角坐标系中，点P （-4,2）向右平移7个单位长度得到点P 1，点P 1绕原点逆时针旋转90º得到点P 2，则点P 2的坐标是（ ）A. (2,3)-B. (3,2)-C. (2,3)-D. (3,2)-8．如图，AD 是ABC ∆的角平分线，DE AC ⊥，垂足为E ，//BF AC ，交ED 的延长线于点F .若BC 恰好平分ABF ∠,2AE BF =，则下列四个结论:①DE DF =;②DB DC =; ③AD BC ⊥;④3AC BF =.其中，正确的结论有（ ）A . ①②③④B ．①②C ． ①②③D ．②③④二、填空题（本大题共8小题，每小题2分，共16分）O A B C P Q 11．36的平方根是 ．12．若y ＝+﹣3，则x +y ＝ ．13．如图，AB ＝AC ，则数轴上点C 所表示的数为________．14．据统计：我国微信用户数量已突破 8.87 亿人，近似数 8.87 亿精确到 位．15．若点A 的坐标为（6，3），O 为坐标原点，将OA 绕点O 按顺时针方向旋转900得到OA ＇，则点A ＇的坐标为（ ）第16题 第17题 第18题16．如图，在△ABC 中，DM 、EN 分别垂直平分AC 和BC 交AB 于M 、N ，∠ACB ＝118°，则∠MCN 的度数为 ．17．如图，等边△ABC 中，AO ⊥BC ，且AO =2，E 是线段AO 上的一个动点，连接BE ，线段BF与线段BE 关于直线BA 对称，连接OF ，在点E 运动的过程中，当OF 的长取得最小值时，AE 的长为 ．18．如图，在△ABC 中，OA ＝4，OB ＝3，C 点与A 点关于直线OB 对称，动点P 、Q 分别在线段AC 、AB 上（点P 不与点A 、C 重合），满足∠BPQ ＝∠BAO ．当△PQB 为等腰三角形时，OP 的长度是 ．三、解答题（共60分）19．（10分）计算：(1) √(−3)2+√−643−|1−√3| (2) ()01214----π20．（10分）求下列各式中x 的值:(1) 9x 2 - 121 = 0 ； （2）（x ﹣1）3-27＝0．FE O C B A21.（10分）（1）如图1，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为A （－3，5），B （－2，1），C （－1，3）．①画出△ABC 关于x 轴的对称图形△A 1B 1C 1；②画出△A 1B 1C 1沿x 轴向右平移4个单位长度后得到的△A 2B 2C 2；③如果AC 上有一点M （a ，b ）经过上述两次变换，那么对应A 2C 2上的点M 2的坐标是 ．（2）请在图2用无刻度的直尺在图中以AB 为一边画一个面积为18的长方形ABMN ．（不要求写画法，但要保留画图痕迹）22.（10分）如图，已知在四边形ABCD 中，点E 在AD 上，∠BCE ＝∠ACD ，∠BAC ＝∠D ，BC ＝CE ．（1）求证：AC ＝CD ．（2）若AC ＝AE ，∠ACD ＝80°，求∠DEC 的度数．23.（10分））如图，四边形ABCD 中，∠BAD ＝90°，∠DCB ＝90°，E 、F 分别是BD 、AC 的中点．（1）请你猜想EF 与AC 的位置关系，并给予证明；（2）若∠ABC ＝45°,AC ＝16时，求EF 的长．x O 4 3 2 1 －4 4 321 －3 －2 －1 －1 －2 －3 －4 y5 5 －5 －5 B A C （图2） B A (图1)24.（满分10分）如图，在等边△ABC中，AB＝9cm，点P从点C出发沿CB边向点B点以2cm/s的速度移动，点Q从B点出发沿BA边向A点以5cm/s速度移动．P、Q两点同时出发，它们移动的时间为t秒钟．（1）请用t的代数式表示BP和BQ的长度: BP= ,BQ= ．（2）若点Q在到达点A后继续沿三角形的边长向点C移动，同时点P也在继续移动，请问在点Q从点A到点C的运动过程中，t为何值时，直线PQ把△ABC的周长分成4：5两部分？（3）若P、Q两点都按顺时针方向沿△ABC三边运动，请问在它们第一次相遇前，t为何值时，点P、Q能与△ABC的一个顶点构成等边三角形？。